Смольников А.П. Теория автоматического управления
Подождите немного. Документ загружается.


223
2
1
()
Н
X
Wa
X
≈
≈
=
(27.15)
1
2
()
Л
X
Wj
X
ω
≈
≈
=− , (27.16)
где
2
X
≈
и
1
X
≈
- изображения Фурье для синусоидальных сигналов.
Перемножим (27.15) и (27.16) и получим
1),()()(
−
=
=
ω
ω
jaWjWaW
Р
Л
H
, (27.17)
при
П
ω
ω
= ,
П
aa
=
.
Выражение (27.17) представляет необходимое условие для
существования автоколебаний в системе и называется
условием
гармонического баланса
.
Уравнение (27.17) согласуется с условием нахождения линейной
системы на границе устойчивости. По критерию Найквиста в линейной
системе будут автоколебания, если годограф
W
Р
(jω) пройдет через точку (–1,
j
0),то есть при некоторой частоте ω = ω
п
, W
Р
(jω
п
) = –1.
Основные задачи, решаемые с помощью метода гармонической
линеаризации, это исследование автоколебательного режима в заданной
нелинейной системе и определение условий отсутствия этого режима.
27.5. Графоаналитический метод определения параметров
автоколебательного режима и его устойчивости
Практически пользоваться выражением (27.17) неудобно, так как
требуется подобрать два параметра, поэтому задачу решают графически.
Для этого запишем (27.17) следующим образом
),(
)(
1
)( aM
aW
jW
Н
Н
Л
−=−=
ω
(27.18)
где:
–M
Н
(a) – обратный комплексный коэффициент передачи НЗ, который
равен
)()(
1
)(
aqjaq
aM
Н
′
+
−=−
. (27.19)
Уравнение (27.18) можно решить графически. Для этого нужно
построить на комплексной плоскости годографы линейной части системы

224
)()()(
ω
ω
ω
jVUjW
Л
+
=
и обратного комплексного коэффициента передачи НЗ
)()()( ajVaUaM
H
+
=
−
.
В точке пересечения годографов (рис. 27.13)
выполняется условие (27.18) и могут
существовать автоколебания.
Параметры их определяются следующим
образом: значение частоты ω
п
определяют из
годографа линейной части
W
Л
(jω), а значение
амплитуды
a
п
определяется из годографа –
M
Н
(a).
Пересечение графиков показывает, что в
системе возможны автоколебания.
Следующим этапом является определение
устойчивости этих автоколебаний.
Анализ устойчивости системы и устойчивости предельного цикла.
Запишем условие гармонического баланса в следующем виде.
1
)(
)(
)]()([
−=
+ aj
м
л
нл
e
аA
A
ϕωϕ
ω
. (27.20)
Здесь
А
м
(a) = |M
н
(a)| – модуль передачи нелинейного элемента,
)(arg)( a
W
a HH =
ϕ
.
Уравнение (27.20) можно представить в виде двух уравнений
1
)(
)(
=
аA
A
м
л
ω
, (27.21)
φ
л
(ω) + φ
н
(а) = – (2m+1) π ; где m = 0, ±1, ±2,…
Допустим, получили следующее расположение годографов (рис.
27.14).
Im
Re
ω
W
л
(
j
ω
)
a
п
ω
п
–
M
н
(
a
)
a
Рис. 27.13
a
Рис. 27.15
Im
Re
D
0
D
1
W
л
(jω)
1`→ ←
2
1``
1
–M
н
(a)
Im
Re
D
0
D
1
W
л
(jω)
–M
н
(a)
Рис. 27.14

225
Пусть весь годограф нелинейного звена лежит в области
D
0
, то есть
условие (27.20) не выполняется, так как
1
)(
)(
<
аA
A
м
л
ω
, значит |W
p
(a, jω)| < 1 и в
соответствии с критерием Найквиста система устойчива и в ней будут
затухающие колебания.
Аналогично можно показать, что если весь годограф
–M
н
(а) лежит в
области
D
1
, то система будет неустойчива и в ней будут существовать
расходящиеся колебания.
Если годографы пересекаются (рис. 27.15) , то в системе возможны
автоколебания в точках 1 и 2. Определим, где автоколебания устойчивы?
В точке 1– амплитуда –
а
п
; в точке 1`– амплитуда – (а
п
+ ∆a); в точке
1``– амплитуда
– ( а
п
– ∆a).
Пусть существуют автоколебания в точке 1 с параметрами
а
п
и ω
п
.
Допустим, произошло увеличение амплитуды
а
п
+ ∆a (точка 1`). Рабочая
точка находится в области
D
0
, то есть система устойчива и амплитуда
колебаний уменьшится до
а
п
.
Пусть амплитуда колебаний уменьшается, то есть
а
п
– ∆a (точка 1``).
Рабочая точка находится в области
D
1
, то есть система неустойчива и
амплитуда колебания возрастет до
а
п
.
Следовательно, точка 1 соответствует устойчивому предельному
циклу.
Рассмотрим точку 2.
Пусть
а понижается, то есть а
п
– ∆a. В этом случае система устойчива и
колебания затухающие. Следовательно, точка 2 соответствует
неустойчивому предельному циклу.
На основе проведенного анализа сформулируем правило определения
устойчивости автоколебаний: автоколебания устойчивы, если годограф
W
Л
(jω) не охватывает точку на годографе –M
H
(a), в которой a = a
п
+ Δa,
a > 0.
Пример. Метод гармонического баланса.
k=10c
-1
b=0.5,
c=10.
Определить, возможны ли автоколебания и если возможны, то найти
их параметры.
Комплексный коэффициент передачи нелинейного звена будет равен
W
н
(а)=q(a)+jq`(a),
где
x
2
x
вх
=0
x
1
К/Р
X
вых
–
Рис. 27.16
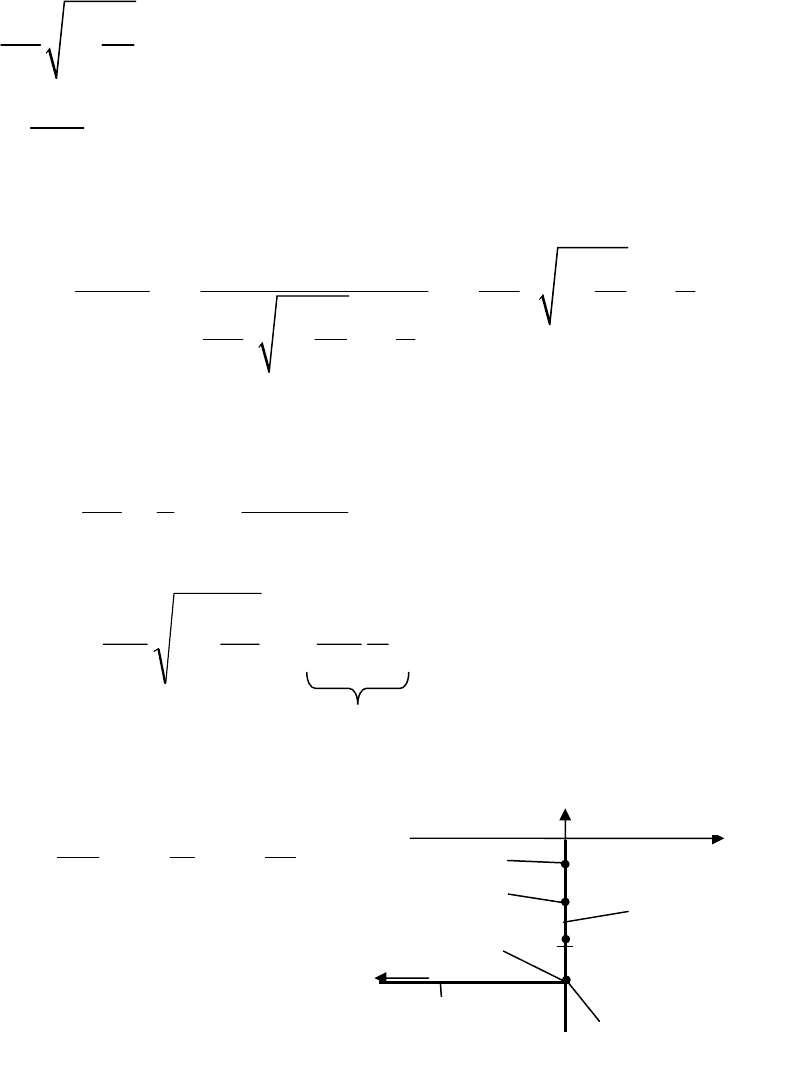
226
2
2
2
4
() 1 , ,
4
`( ) , .
Cb
qa a b
aa
Сb
qa a b
a
π
π
=− ≥
=− ≥
Тогда обратный комплексный коэффициент передачи примет вид
2
2
2
11
() 1
() 4
4
(1 )
н
н
abb
M
aj
Wa C a a
Cbb
j
aaa
π
π
⎛⎞
−=−=− =− −+
⎜⎟
⎜⎟
⎝⎠
−−
Построим его
1) a = b = 0.5
04.0
4
5.014.3
4
)( j
C
j
b
b
j
C
a
aM
н
−=
⋅
−=⋅−=−
π
2) a>b
соnst
Годограф линейной части строим по выражению
ω = 100 W
л
(jω) = -j0.1
ω = 250 W
л
(jω) = -j0.04
ω = 500 W
л
(jω) = -j0.02
ω = 1000 W
л
(jω) = -j0.01
Годографы построены на рис. 27.17.
Автоколебания возможны и имеют параметры:
a = b = 0.5; ω =250 рад/с .
28.
МЕТОД ЛЯПУНОВА
28.1. Понятие о знакоопределенных, знакопостоянных и знакопеременных функциях
a
b
C
a
j
a
b
C
a
aM
н
4
1
4
)(
2
2
ππ
−−−=−
ωωω
ω
10
)( j
k
j
j
k
jW
л
−=−==
-0.04
-0.03
Im
а
ω=500
-0.01
ω=1000
ω=250
-М
Н
(а)
a=
b
=0.5
W
Л
(
j
ω
)
Re
Рис. 27.17
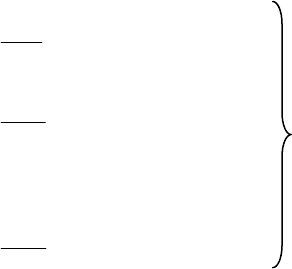
227
Пусть имеется функция нескольких переменных
12
( , ,...., )
n
VVxx x= .
При 2
n = эта функция может быть изображена на фазовой плоскости,
при 3
n = – в трехмерном пространстве. В каждой точке пространства
функция
V имеет определенное значение.
Будем рассматривать только такие функции, которые обращаются в
нуль в начале координат, то есть при
x
1
= x
2
=…= x
n
= 0, (0,0,....,0) 0V
=
.
Кроме того,
V должна быть непрерывна в некоторой области вокруг
начала координат.
Функция
V называется знакопределенной в некоторой области, если во
всех точках этой области она сохраняет один и тот же знак и нигде не
обращается в нуль, кроме начала координат.
Для 2
n = такая функция может иметь вид
22
12
Vx x=+.
Функция V называется
знакопостоянной, если в некоторой области она
сохраняет один и тот же знак, но может обращаться в нуль не только в
начале координат, но и в других точках области.
Пример для 3
n =
22
12 3
()Vxx cx=+ +.
Обращается в нуль на прямой x
2
= -x
1
и x
3
= 0.
Функция V называется
знакопеременной, если в некоторой области
вокруг начала координат она может иметь любой знак
Для 2n =
12
Vx x=+.
28.2. Функция Ляпунова и её производная по времени
Нелинейная система может быть описана системой нелинейных
уравнений:
),..,,(
),..,,(
),..,,(
21
212
2
211
1
nn
n
n
n
xxxF
d
t
dx
xxxF
dt
dx
xxxF
dt
dx
=
=
=
K
(28.1)
где
12
, ,...,
n
x
xx- переменные состояния системы.
12
12
... 0
... 0
n
n
FF F при
xx x
====
====
(28.2)
Любая функция
12
( , ,...., )
n
VVxx x= (28.3)

228
называется функцией Ляпунова, если в качестве переменных
12
, ,...,
n
x
xx взяты переменные системы (28.1).
Производная по времени функции Ляпунова имеет вид
dt
dx
x
V
dt
dx
x
V
dt
dx
x
V
dt
dV
n
n
⋅
∂
∂
++⋅
∂
∂
+⋅
∂
∂
= ...
2
2
1
1
(28.4)
Подставим в (28.4) выражения
i
dx
dt
n
n
F
x
V
F
x
V
F
x
V
dt
dV
⋅
∂
∂
++⋅
∂
∂
+⋅
∂
∂
= ...
2
2
1
1
(28.5)
Следовательно,
),...,,(
21 n
xxxW
d
t
dV
=
(28.6)
Таким образом,
dV
dt
– является функцией отклонений. Причем,
согласно свойства (28.2),
12
0 ... 0
n
W при xx x
=
====. Поэтому к этой
функции можно применить понятие знакоопределенной, знакопостоянной и
знакопеременной функции.
Теорема Ляпунова. Если при заданных в форме (28.1) уравнениях
нелинейной системы
n-го порядка можно подобрать такую
знакоопределенную функцию
12
( , ,...., )
n
VVxx x
=
, чтобы её производная по
времени
12
( , ,..., )
n
Wx x x также была знакоопределенной или
знакопостоянной, но имела знак, противоположный знаку функции
V, то
данная система устойчива.
Пример. Пусть задана нелинейная САУ, которая описывается системой
уравнений:
),,(
),,(
),,(
3213
3
3212
2
3211
1
xxxF
d
t
dx
xxxF
dt
dx
xxxF
dt
dx
=
=
=
(28.7)
Выберем Функцию Ляпунова в виде:
22 22 22
123
V а xbxcx=++ (28.8)
V > 0 при любых x
i,
а,b,c - произвольные вещественные числа.
Будем придавать этой функции постоянные значения
0,С
1
,С
2
,….,
причем
0<С
1
<С
2
… Тогда получим
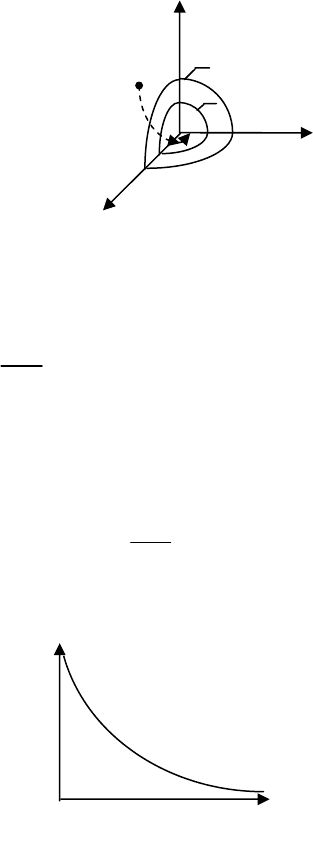
229
22 22 22
123
22 22 22
1231
22 22 22
1232
0,
,
.
V а xbxcx
V а xbxcxC
V а xbxcxC
=++=
=++=
=++=
(28.9)
Возьмем производную от V по времени
22 2
11 1 2 3 2 2 1 2 3 3 3 1 2 3
2 ( , , ) 2 ( , , ) 2 ( , , ) (28.10)
dV
axFxxx bxFxxx cxFxxx
dt
=++
Если полученная функция
12
( , ,..., )
n
Wx x x является знакоопределенной
отрицательной, то есть
,0<=
dt
dV
W
то V убывает во всех точках пространства, кроме начала координат,
Таким образом, при любых начальных
условиях изображающая точка M будет двигаться в
сторону уменьшения функции V, то есть будет
пересекать эллипсоиды и стремиться к началу
координат. А это означает, что все отклонения
системы
321
x,x,x уменьшаются, то есть система
устойчива.
При практическом применении метода наибольшую трудность
вызывает подбор функции V, так как эта задача неоднозначна и не
существует формальных методов нахождения V, поэтому приходится
полагаться на опыт и интуицию.
Однако, несмотря на это, метод применяется не только для
исследования нелинейных систем, но и
при анализе и синтезе адаптивных
законов управления. Адаптивные системы управления относятся к классу
нелинейных систем.
28.3. Формулировка теоремы Ляпунова в векторно-матричной
форме
Х
1
Х
2
Х
3
С
2
С
1
x
1
M
V
t
Рис. 28.2
Рис. 28.1
230
В общем случае, если используется математическое описание САУ в
форме уравнений состояния, то функция Ляпунова часто имеет вид
квадратичной формы, которая включает в себя члены второй степени по x
i
и
x
j
12
11
( , ,.... ) , (28.11)
nn
nijij
ij
Vx x x pxx
==
=
∑∑
где: x - вектор состояния, p
i,j
– коэффициенты.
В векторно-матричной форме
12
( , ,..., )
T
n
Vx x x xPx= (28.12)
где x
T
– вектор-строка, полученная транспонированием вектора x;
P- квадратная определенно положительная симметрическая матрица
типа n×n, элементы которой постоянны, причем P = P
T
.
Критерий Сильвестра.
Квадратичная форма (28.12) положительно определенная, если все “n”
определителей |P
1
|,|P
2
|,…,|P
n
| - положительны.
Пример :
[] []
2112
2
122
2
111
2
2222112
2112
2
111
222121
212111
21
2
1
2221
1211
2121
2
),(
xxpxpxpxpxxp
xxpxp
xpxp
xpxp
xx
x
x
pp
pp
xxxxV
++=++
+=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
=
так как р
12
= р
21
.
Определение устойчивости линейной системы.
Дифференцирование функции Ляпунова в виде (28.12).
Пусть имеем линейную автономную систему, которая описывается
уравнением состояния
xAx=
&
(28.13)
Тогда сопряженная система будет иметь вид
TTT
xxA=
&
(28.14)
Пусть V(
x
)=x
T
Px - функция Ляпунова.
Тогда найдем производную функции Ляпунова по времени
( ) ( ) (28.15)
TT TTT TT
V x x Px x Px x A Px x PAx x A P PA x=+= + = +
&
&&
Введем обозначение A
T
P +PA= - Q. ( 28.16)
Тогда если матрица Q положительно определена, то система (28.13)
асимптотически устойчива, так как

231
( ) 0 (28.17)
T
WVx xQx==−<
&
Эти результаты применяют при синтезе адаптивных систем
управления, которые обычно содержат в своем составе как линейные, так и
нелинейные части.
29.УСЛОВИЯ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ
НЕЛИНЕЙНЫХ СИСТЕМ
29.1. Понятие абсолютной устойчивости
Пусть имеем нелинейную систему с одной нелинейной функцией
x
2
=F(x
1
) (29.1)
Пусть на характеристику НЗ наложены ограничения
1
1
()
0
н
Fx
k
x
≤< (29.2)
232
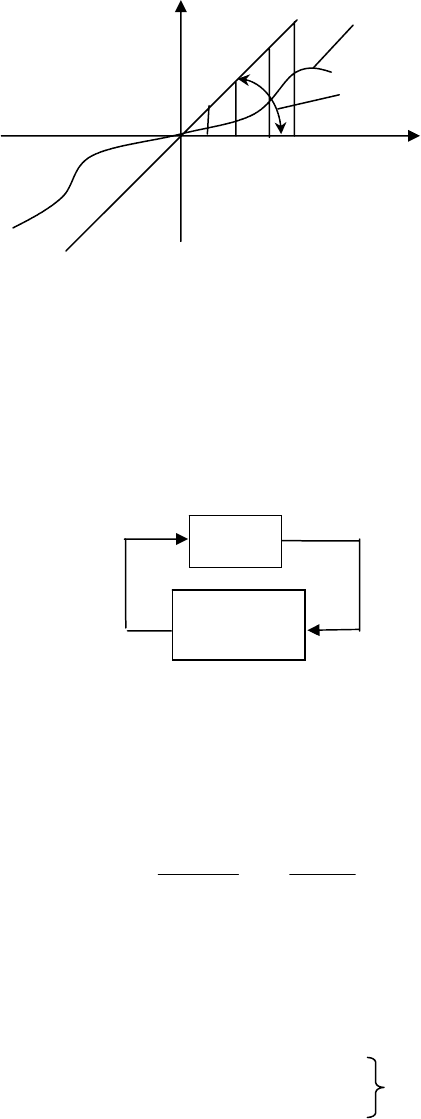
x
2
x
1
аrctg k
н
F(x
1
)
Условие (29.2) графически изображено на рис. 29.1 и показывает, что
нелинейная функция должна находиться внутри заштрихованного сектора.
Примером такой функции могут служить характеристики АЦП и ЦАП.
Условие абсолютной
устойчивости гласит, что при любой
нелинейности, удовлетворяющей
ограничению (29.2), нелинейная
система будет устойчива.
29.2. Частотный критерий абсолютной устойчивости В. М.
Попова
Пусть нелинейная система содержит однозначную нелинейность и в
ней выделены линейная часть и нелинейное звено (рис. 29.2).
НЗ описывается уравнением (29.1) и удовлетворяет ограничениям
(29.2).
Пусть линейная часть имеет передаточную функцию (29.3) и
описывается уравнением (29.4):
1
2
()
()
()
() ()
Xp
Rp
Wp
Xp Qp
==−
(29.3)
12
() () () ()QpX p RpX p=− , (29.4)
где Q(p) и R(p) – полиномы степени n и m
Q(p)=a
0
p
n
+ a
1
p
n-1
+…+ a
n
R(p)=b
0
p
m
+ b
1
p
m-1
+…+ b
m
На линейную часть накладываются следующие ограничения:
Характеристическое уравнение линейной части Q(p) = 0 имеет все
простые корни с отрицательной вещественной частью и не более двух
(29.5)
Рис. 29.1
F(x
1
)
Линейная
часть
x
2
x
1
Рис. 29.2
