Смольников А.П. Теория автоматического управления
Подождите немного. Документ загружается.

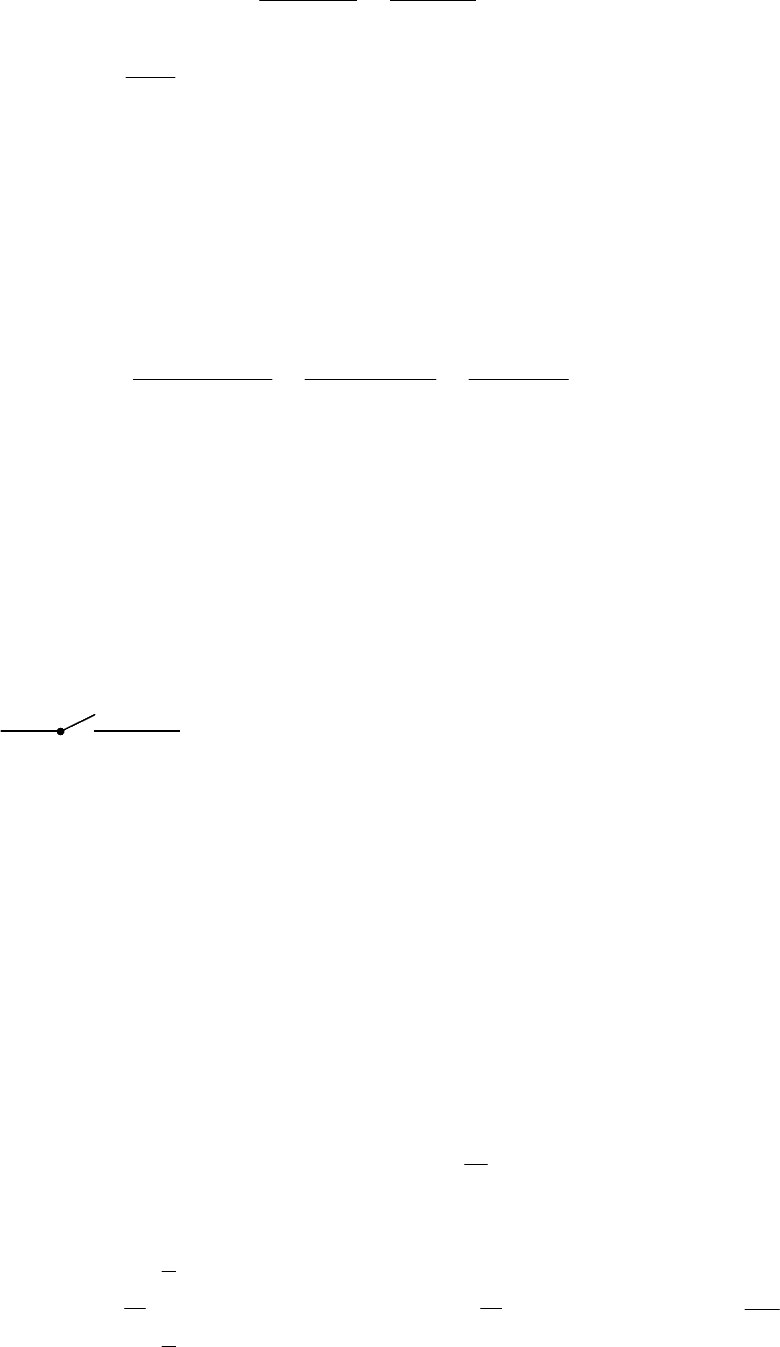
153
X
*
(p) =
11
1
0
−
=
−
=
−
∞
=
−
∑
pT
pT
pT
l
plT
e
e
e
e
X (z) =
1−z
z
.
Пример 2.
Дана экспоненциальная функция. Найти z-преобразование.
x(t) =
at
e
−
x(lT) =
alT
e
−
aTaTaT
aTaT
l
l
ez
z
zeze
zezezlTxzX
−−−−
−−
∞
=
−
−
=
−
=
−
=
=+++==
∑
11
21
0
1
1
)(1
1
...)()(1)()(
17. ОСОБЕННОСТИ СПЕКТРОВ ДИСКРЕТНЫХ СИГНАЛОВ
17.1. Связь между частотными спектрами непрерывных и
дискретных величин
Рассмотрим идеальное импульсное звено (рис. 17.1).
Рис. 17.1
x
*
(t) =
∑
∞
=
−
0
)()(
l
lTtlTx
δ
, (17.1)
Так как x(t) = 0 при t
<
0 и
δ
(t-lT) = 0 при t
≠
lT, то выражение (17.1)
может быть записано
x
*
(t) =
∑
∞
−∞=
−
l
lTttx )()(
δ
. (17.2)
Выражение
∑
∞
−∞=
−
l
lTt )(
δ
может быть представлено рядом Фурье в
комплексной форме, то есть
1
()
ии
jr t jr t
r
lr r
tlT Ce e
T
ω
ω
δ
∞∞ ∞
=−∞ =−∞ =−∞
−= =
∑∑ ∑
(17.3)
где коэффициенты разложения определяются:
T
dtelTt
T
C
t
и
jr
T
Tl
r
1
)(
1
2
2
=
⎥
⎦
⎤
⎢
⎣
⎡
−=
−
−
−
∞
−∞=
∫
∑
ω
δ
для любого r,
T
и
π
ω
2
= (17.4)
x
x
*
154
Следовательно, подставив (17.3) в (17.2), получим
x
*
(t) =
∑
∞
−∞=
r
t
и
jr
e
T
tx
ω
1
)(
(17.5)
Преобразование Фурье для x
*
(t) выражается
X
*
( j
ω
) =
0
1
()
и
jr t
jt
r
x
teedt
T
ω
ω
∞
∞
−
=−∞
⎡⎤
⎢⎥
⎢⎥
⎣⎦
∑
∫
=
()
0
1
()
и
jrt
r
x
te dt
T
ωω
∞
∞
−−
=−∞
∑
∫
(17.6)
[]
()
0
() ( )
и
jrt
и
xte dt X j r
ωω
ωω
∞
−−
=−
∫
(17.7)
Поэтому (17.6) имеет вид:
X
*
( j
ω
) =
[]
∑
∞
−∞=
−
r
и
rjX
T
)(
1
ωω
(17.8)
Изменяя порядок суммирования, то есть подставив (r) вместо (-r),
получим
X
*
( j
ω
) =
[]
∑
∞
−∞=
+
r
и
rjX
T
)(
1
ωω
. (17.9)
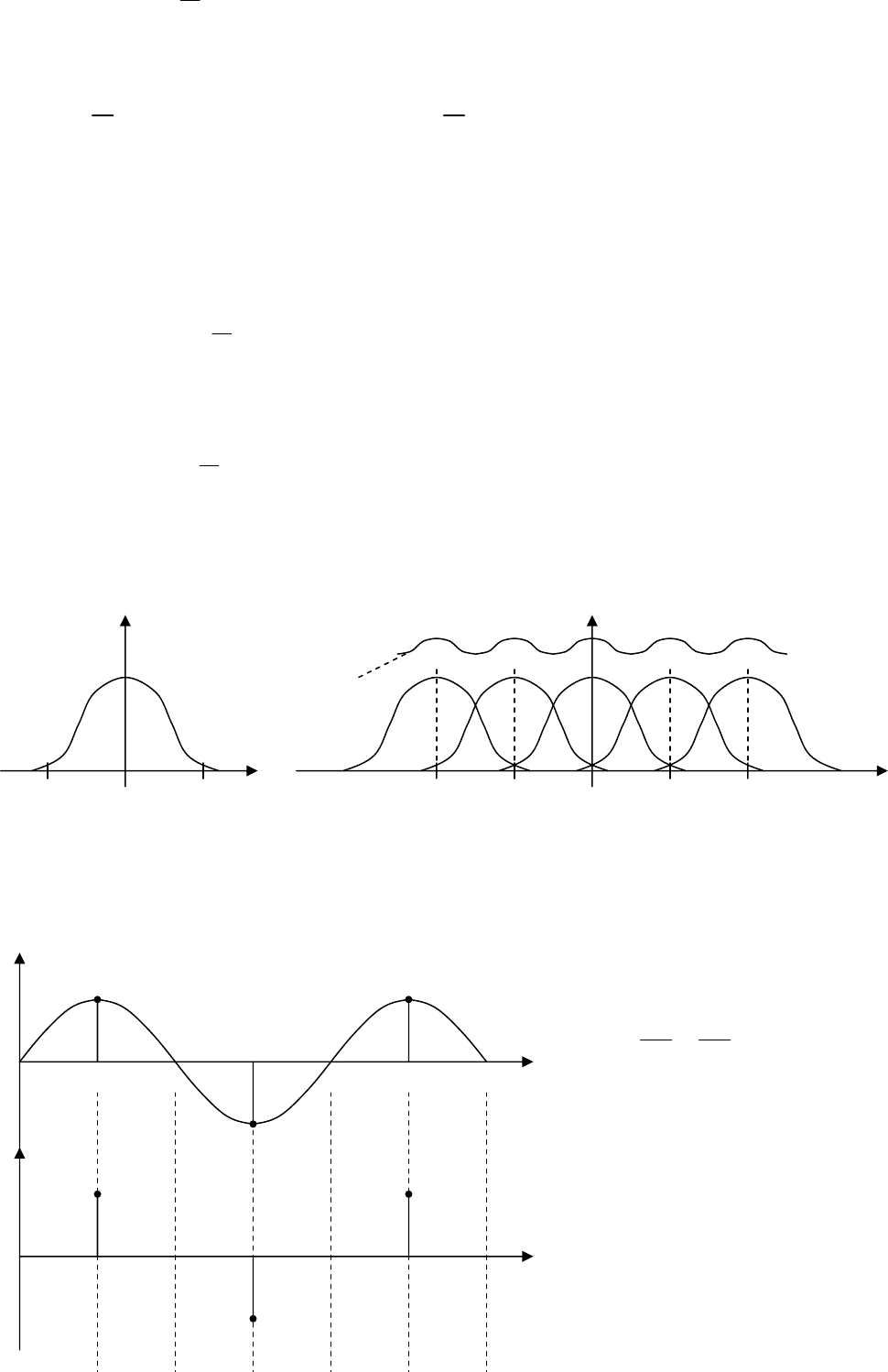
Выражение (17.9) показывает, что частотный спектр x
*
(t) представляет
сумму частотных спектров непрерывной величины, смещенных на величину
ω
и
.
а Рис. 17.2 б
Периодичность частотной характеристики составляет особенность
импульсной системы и физически связана со свойством импульсного
элемента одинаково реагировать на кратные частоты входного сигнала
|X(j
ω
)|1/Т
ω
и
-
ω
и
ω
|X
*
(j
ω
)|
ω
и
-
ω
и
ω
2
ω
и
-2
ω
и
0
|X
*
(j
ω
)|
r=2 r=1
r=0
r=-1 r=-2
ω
1
=
T
T
4
2
2
π
π
=
T – период квантования
T
x
вх1
2T 4T 5T 6T
t
x
вых(lT)
t
155
2
1
4
3
4
3
T
T
ω
ω
==
Рис. 17.3
Изображения непрерывного x(t) и дискретного x
*
(t) сигналов связаны
отношением
X
*
( p) =
∑
∞
−∞=
+
r
и
jrpX
T
)(
1
ω
.
17.2.
Прохождение сигналов через импульсную САУ
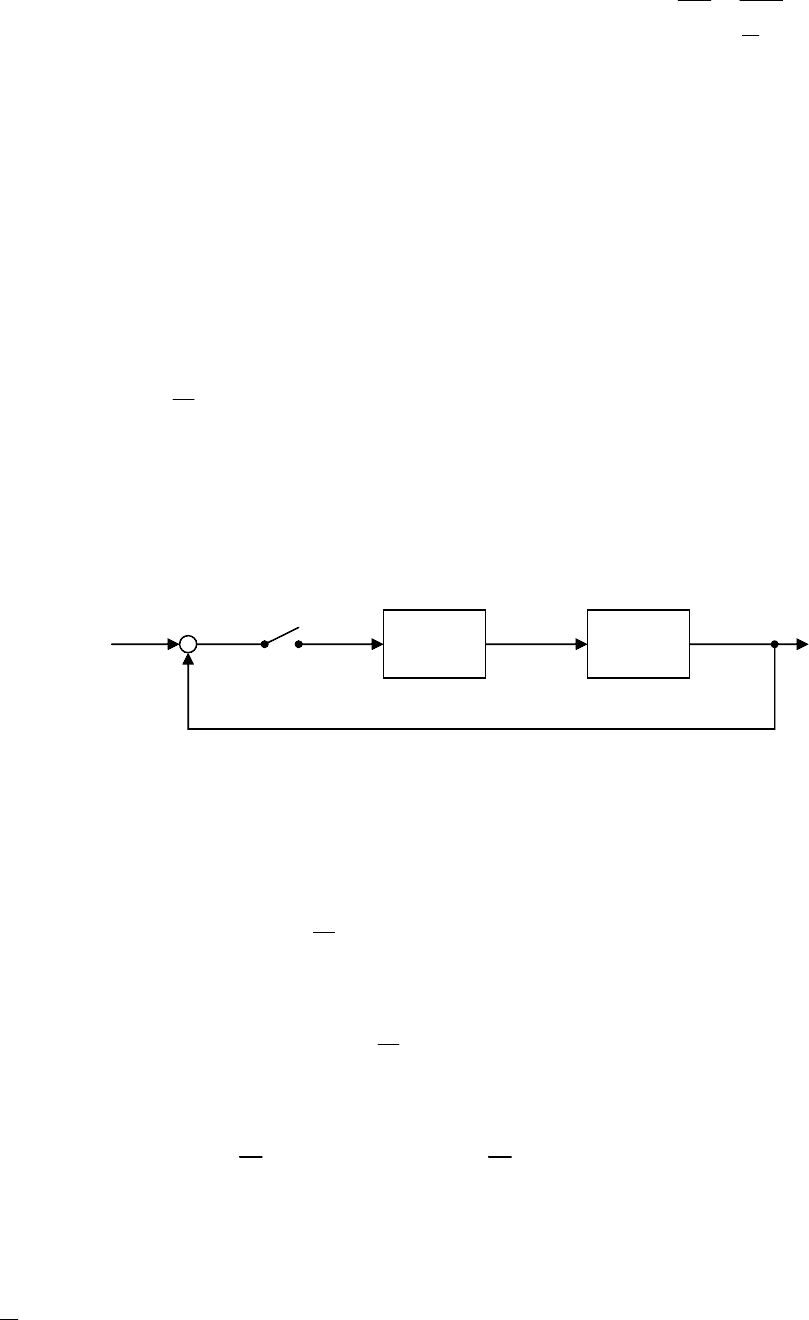
Рассмотрим эквивалентную схему
Рис. 17.4
Будем считать (для простоты), что x(0)=0 и в системе имеют место
нулевые начальные условия.
Найдем спектр выходной величины:
X
вых
( j
ω
)=W
фн
(j
ω
)
⋅
X
*
( j
ω
), (17.10)
где X
*
( j
ω
)=
[]
∑
∞
−∞=
+
r
и
rjX
T
)(
1
ωω
(17.11)
X
вых
( j
ω
)= W
фн
(j
ω
)
⋅
[]
∑
∞
−∞=
+
r
и
rjX
T
)(
1
ωω
(17.12)
Если выделить в (17.12) слагаемое для r = 0, то получим
0
11
() ()() () [( )
r
В
ЫХ ФН ФН и
r
r
Xj WjXj Wj Xjr
TT
ω
ωω ω ωω
=
∞
=∞
≠
=+⋅+
∑
(17.13)
Первое слагаемое представляет собой спектр выходного сигнала,
который бы имел место в непрерывной системе с частотной характеристикой
T
1
W
фн
(j
ω
).
W
ф
(p)
x
x
*
ИИЗ
W
Н
(p)
x
вх
–
x
И
x
вых
156
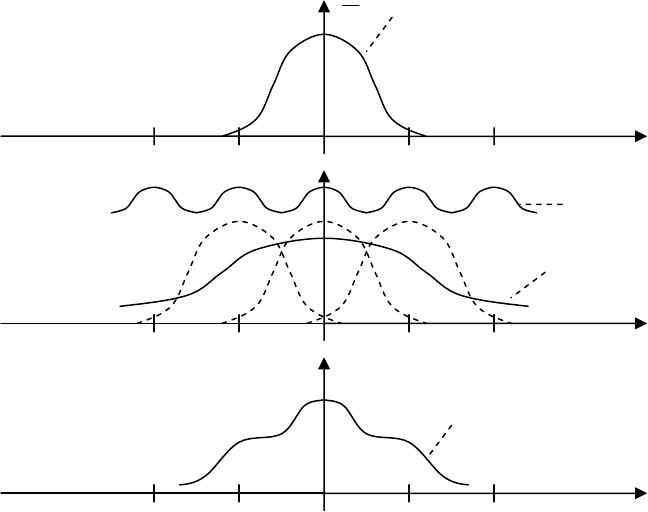
Второе слагаемое отражает влияние импульсного звена. Наличие
импульсного элемента приводит к появлению в спектре выходного сигнала
высокочастотных составляющих и в результате в общем случае невозможно
связать с помощью частотной функции (или передаточной функции) спектры
сигналов X(j
ω
) и X
вых
(j
ω
) подобно тому, как это делается в непрерывной
системе.
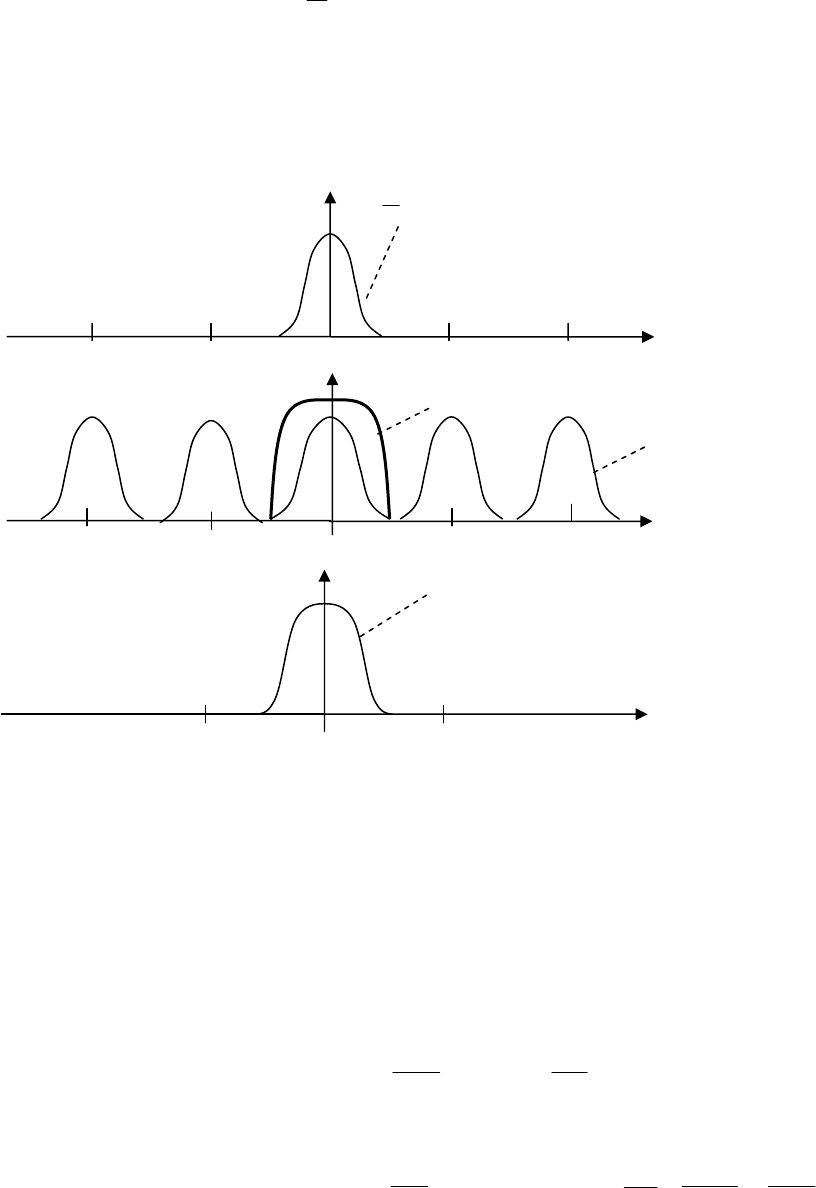
Рис. 17.5
То есть наличие импульсного элемента приводит к появлению в
спектре выходного сигнала высокочастотных составляющих, которых не
было в спектре сигнала X(j
ω
).
17.3. Прохождение сигналов через ИСАУ при выполнении условий
теоремы Котельникова
Существует случай, когда можно связать X(j
ω
) и X
вых
(j
ω
). Выберем
ω
и
≥
2
ω
с
, (17.14)
где
ω
с
– граничная частота входного сигнала x(t).
Кроме того, пусть
T
1
|X(j
ω
)|
ω
и
-
ω
и
ω
2
ω
и
-2
ω
и
0
|X
*
(j
ω
)|
ω
и
-
ω
и
ω
2
ω
и
-2
ω
и
0
|W
фн
(j
ω
)|
ω
0
|X
вых
(j
ω
)|
-
ω
и
-2
ω
и
ω
и
2
ω
и
157
W
фн
(j
ω
)=0 при
ω
>
ω
с
(17.15)
Тогда X
вых
( j
ω
)=
T
1
W
фн
(j
ω
)
⋅
X(j
ω
) (17.16)
В этом случае импульсная система эквивалентна непрерывной
системе, причем при выполнении условий (17.14) и (17.15) идеальное звено
по своим свойствам эквивалентно безынерционному звену с коэффициентом
усиления 1/T.
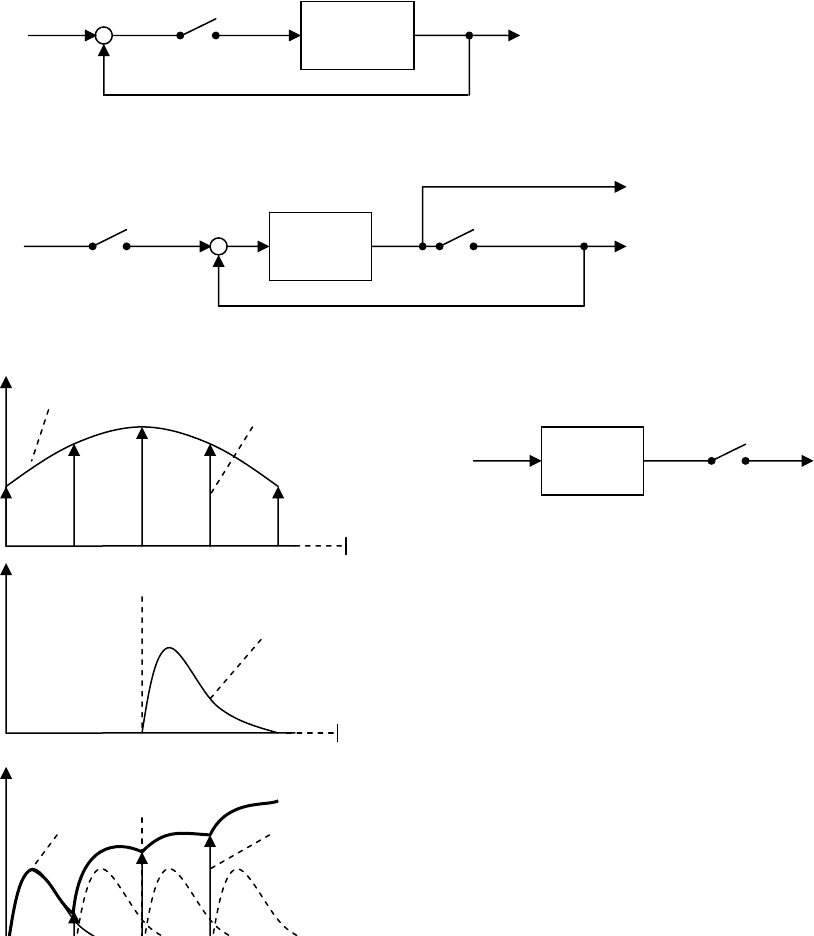
Рис. 17.6
Вывод (17.16) при условиях (17.15) и (17.14) получен В.А.
Котельниковым и носит название теоремы Котельникова. Смысл теоремы
состоит в том, что если требуется передать сигнал x(t) с ограниченным
спектром X(j
ω
), то достаточно передать дискретные значения x
*
(t) с периодом
T
≤
c
f2
1
или T
<
c
ω
π
.
Это вытекает из (17.14).
Если
ω
и
≥
2
ω
с,
то получим
T
π
2
≥
ω
с
или T
≤
c
ω
π
=
cc
ff 2
1
2
=
π
π
.
ω
T
1
|X(j
ω
)|
ω
и
-
ω
и
2
ω
и
-2
ω
и
0
ω
с
ω
ω
и
-
ω
и
2
ω
и
-2
ω
и
0
ω
с
|W
фн
(j
ω
)|
|X
*
(j
ω
)|
ω
и
-
ω
и
ω
0
ω
с
|X
вых
(j
ω
)|
158
18. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ИМПУЛЬСНЫХ СИСТЕМ
18.1. Передаточная функция и частотная передаточная
функция разомкнутой импульсной системы
Ранее было установлено, что в общем случае отсутствует
пропорциональная связь между спектрами сигналов x(t) и x
вых
(t).Однако
такая связь существует между спектрами и изображениями дискретных
сигналов x
*
(t) и x
*
вых
(t).
Целесообразность отыскания такой связи следует из возможности
представления схемы (рис. 18.1)
Рис. 18.1
в следующем виде
Рис. 18.2
Рассмотрим прямую цепь системы
Рис. 18.3
W
фн
(p)
x
*
ИИЗ
x
вх
–
x
вых
ИИЗ
x
*
вых
x
вых
x
*
вх
W
фн
(p)
x
x
*
ИИЗ
x
вх
-
x
вых
x
*
= (x
вх
- x
вых
)
*
= x
*
вх
- x
*
вых
W
фн
(p)
x
*
ИИЗ
x
*
вых
x
вых
x(t)
t
T 2T 3T 4T
x
*
(t)
iT
x
вых,i
(t)
lT
и
t
lT
и
x
вых
(t)
x
*
вых
(t)
159
Рис. 18.4
Реакция системы на импульс в i-й момент и имеющий площадь x(iT),
равна (рис. 18.4, б)
x
вых,i
(t) = x(iT) w
фн
(t - iT),
где w
фн
(t) – весовая функция приведенной непрерывной части.
Выходную величину x
вых
(t) можно представить путем суммирования i-х
составляющих
x
вых
(t)=
∑
=
−
l
i
фн
iTtwiTx
0
)()(
для lT
≤
t
≤
(l+1)T;
Дискретный входной сигнал, поступающий на вход прямой цепи (рис.
18.3), описывается выражением:
x
*
(t) =
∑
∞
=
−
0
)()(
i
iTtiTx
δ
(18. 1)
Пусть приведенная непрерывная часть имеет весовую функцию, то
есть реакцию на
δ
– функцию вида w
фн
(t), тогда ее выходной сигнал
выражается суммой:
x
вых
(t) =
∑
∞
=
−
0
)()(
i
фн
iTtwiTx
(18. 2)
Дискретные значения выходного сигнала x
вых
(lT) определяют из (18.2)
при t=lT.
x
вых
(lT) =
∑
∞
=
−
0
))(()(
i
фн
TilwiTx (18. 3)
Для получения изображения Лапласа от x
*
вых
(t) воспользуемся
уравнением дискретного преобразования Лапласа
X
*
вых
(p) =
000
() () (( )).
plT plT
вых фн
lli
x
lT e x iT w l i T e
∞∞∞
−−
===
=−
∑∑∑
(18. 4)
Положим k = l - i
X
*
вых
(p) =
piTpkT
iki
фн
eekTwiTx
−−
∞
−=
∞
=
∑∑
.)()(
0
(18. 5)
Так как w
фн
(t) = 0 при t < 0, то заменим нижний предел суммы (вместо
k = -i запишем k = 0) и получим

160
X
*
вых
(p) =
00
() ()
pkT piT
фн
ki
w kTe xiTe
∞∞
−−
==
∑∑
, (18. 6)
где W
p
*
(p) – передаточная функция разомкнутой импульсной системы.
Значит, передаточная функция разомкнутой импульсной системы
равна отношению изображений выходного и входного дискретных сигналов,
то есть
W
p
*
(p)=
∑
∞
=
−
=
0
*
*
)(
)(
)(
k
pkT
фн
вых
ekTw
pX
pX
. (18. 7)
Аналогичные равенства существуют и для изображений Фурье
X
*
вых
(j
ω
) = W
p
*
( j
ω
)
⋅
X
*
( j
ω
) (18. 8)
где W
p
*
(j
ω
)=
∑
∞
=
−
0
)(
k
kTj
фн
ekTw
ω
– частотная передаточная функция
разомкнутой импульсной системы.
W
p
*
(jω) можно найти и другим способом, используя связь между
спектрами непрерывных и дискретных величин,
W
p
*
(j
ω
)=
T
1
[]
∑
∞
−∞=
+
r
ифн
rjW )(
ωω
, (18. 9)
где W
фн
(j
ω
) – частотная передаточная функция непрерывной части.
Комплексный коэффициент передачи W
p
*
(j
ω
) является спектром
функции w
*
фн
(t) и обладает свойствами спектров дискретных сигналов, то есть
он периодичен по оси частот с периодом
ω
и
.
Поэтому амплитудно-фазовые характеристики импульсных систем
можно рассматривать в диапазоне
22
ии
ω
ω
ω
≤≤− .
18.2. Определение передаточной функции разомкнутой системы по
передаточной функции непрерывной части
Передаточная функция разомкнутой системы может быть определена
следующими методами:
1. Ранее были получены выражения для нахождения передаточной
функции и частотной передаточной функции на основе известной функции
веса w
фн
(t) приведенной непрерывной части
W
p
*
(p)=
∑
∞
=
−
0
)(
l
plT
фн
elTw , (18. 10)
W
p
*
(j
ω
)=
∑
∞
=
−
0
)(
l
lTj
фн
elTw
ω
. (18.11)
X
*
(p) W
p
*
(p)
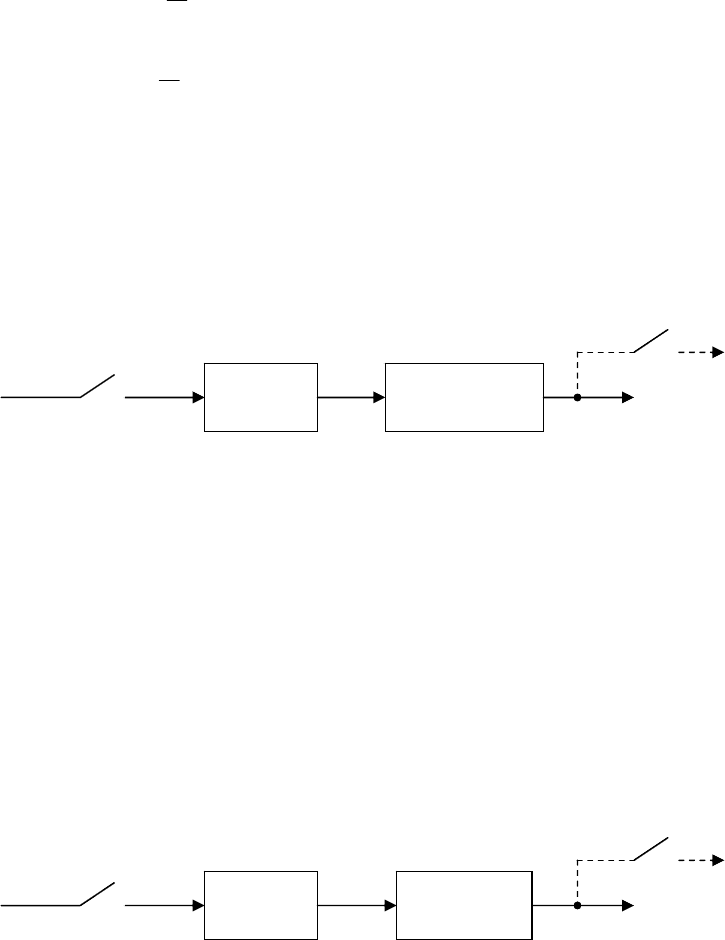
161
Передаточные функции (18.10) и (18.11) являются изображением
дискретного сигнала w
*
фн
(t).
2. Передаточные функции разомкнутой системы W
p
*
(p) и W
p
*
(j
ω
) можно
найти, если известны передаточные функции приведенной непрерывной части
W
фн
(p) и W
фн
(j
ω
) по выражениям
W
p
*
(p)=
T
1
∑
∞
−∞=
+
r
ифн
jrpW )(
ω
, (18. 12)
W
p
*
(j
ω
)=
T
1
[]
∑
∞
−∞=
+
r
ифн
rjW )(
ωω
. (18. 13)
Однако практически использовать выражения (18. 10) и (18.12) сложно
и их редко применяют для определения W
p
*
(p) в компактной форме.
Выражение (18.13) используют при расчетах на ЭВМ.
3. Для получения передаточной функции W
p
*
(p) целесообразно
применять следующую методику.
Пусть имеем эквивалентную схему
Рис. 18.5
Передаточная функция ФЗ, как правило, зависит от p и e
-pT
и может
быть представлена в виде произведения:
W
Ф
(p) = W
Т
(p) · W
ФНЧ
(p),
где W
Т
(p) — трансцендентная часть, зависящая от оператора e
-pT
,
W
ФНЧ
(p) — передаточная функция непрерывной части ФЗ.
Относя непрерывную часть ФЗ к непрерывной части системы, получим
эквивалентные непрерывную и дискретную части системы, а именно:
W
Т
(p) — дискретная часть системы,
W
ПНЧ
(p) = W
ФНЧ
(p) · W
Н
(p) — приведенная непрерывная часть.
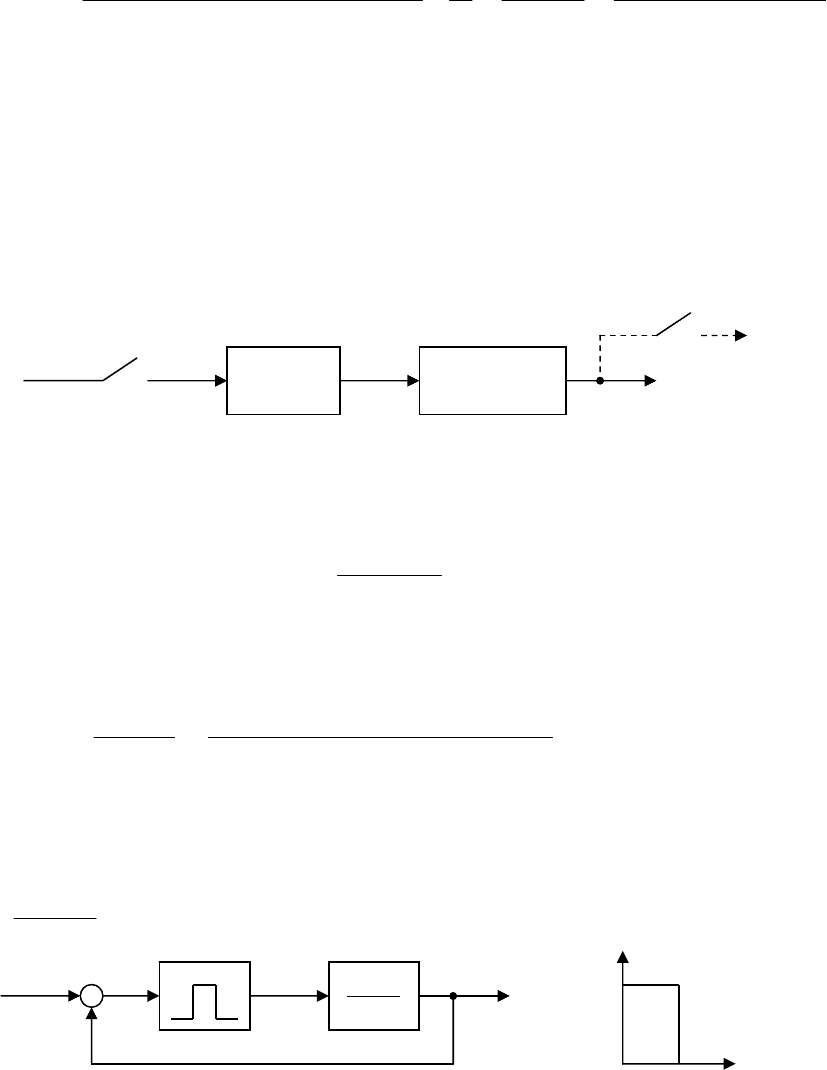
Тогда схема примет вид
Рис. 18.6
Будем рассматривать все сигналы разомкнутой системы только в
моменты замыкания ключа ИИЗ. Для этого на выходе системы установим
фиктивный импульсный элемент, тогда все передаточные функции станут
дискретными передаточными функциями. Обозначим операцию перевода
W
Ф
(p)
W
Н
(p)
x
*
вых
x
вых
x
*
НЧ
ИИЗ
x
x
И
ФЗ
W
Т
(p) W
ПНЧ
(p)
x
x
*
вых
x
вых
x
*
ИИЗ
162
передаточной функции аргумента p в дискретную передаточную функцию
аргумента e
pT
оператором Z, то есть
W
*
(p) = Z[W(p)].
Операцию перевода W(p) в W
*
(p) удобно осуществлять, разлагая
выражение W(p) на простые дроби, то есть представляя передаточную
функцию в виде суммы передаточных функций типовых динамических
звеньев, например:
W(p) =
)12)(1(
)(
22
21
1
+++ TppTpTp
pB
ε
=
12
1
2
22
2
1
++
+
+
+
+
pTpT
DpC
pT
B
p
A
ε
.
Для этого можно применить метод неопределенных коэффициентов.
Затем для каждого из слагаемых по таблицам дискретного преобразования
Лапласа находят дискретные передаточные функции, а далее определяют
результирующую передаточную функцию.
Применяя этот подход, можно найти дискретную передаточную
функцию приведенной непрерывной части системы
W
*
П.Н.Ч.
(p) = Z[W
П.Н.Ч.
(p)].
В результате окончательно получим эквивалентную схему импульсной
системы:
Рис. 18.7
Передаточная функция разомкнутой системы будет равна:
W
p
*
(p) = W
Т
(p) · W
*
П.Н.Ч.
(p) =
)(
)(
*
*
pX
pX
вых
.
W
p
*
(p) является трансцендентной функцией и может быть представлена
в виде:
W
p
*
(p) =
n
pTnnpT
m
pTmmpT
cecec
bebeb
pC
pB
+++
+++
=
−
−
...
...
)(
)(
)1(
10
)1(
10
*
*
.
Пример 1. Найти передаточную функцию W
p
*
(p) для импульсной САУ с
прямоугольными импульсами при γ = 1 и с непрерывной частью
W
Н
(p)=
1
1
+pT
k
.
а) б)
Рис. 18.8
W
Т
(p) W
*
ПНЧ
(p)
x
x
*
вых
x
*
ИИЗ
x
вх
–
x
вых
1
1
+pT
k
f(
t
)
t
T
1
