Смольников А.П. Теория автоматического управления
Подождите немного. Документ загружается.

133
ˆ
ˆ
x
-x=(A-LC)(x-x)
&&
.
Известно, что если собственные числа матрицы
[]
A
-LC , т.е. корни
характеристического уравнения системы ”объект-наблюдатель” лежат в
левой полуплоскости, то система устойчива и при
t0→ ошибка оценивания
ˆ
0e= x- x→ , значит вектор
ˆ
x
x→ . Скорость сходимости оценок зависит от
полюсов ”объекта и наблюдателя”.
Пример 1. Построить наблюдатель полного порядка для объекта
второго порядка.
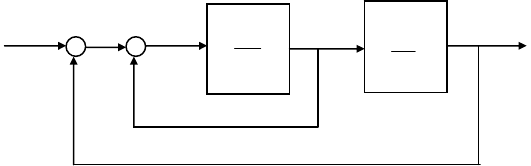
Рис. 14.3. Структурная схема
Уравнения состояния, составленные для объекта на рис. 14.3, имеют
матрицы А, В и С:
1
22
0a
A=
-a -a
⎡⎤
⎢⎥
⎣⎦
;
2
0
B=
a
⎡⎤
⎢⎥
⎣⎦
;
[
]
C= 1 0 .
Так как объект имеет второй порядок, то матрица L имеет вид
11
21
L
L=
L
⎡⎤
⎢⎥
⎣⎦
.
В соответствии с методикой синтеза проведем вычисления:
[]
111 111 11 1
22 21 22 21 2212
0a L 0a L0 -L a
A-LC= - × 1 0 = - =
-a -a L -a -a L 0 -a - L -a
⎡⎤⎡⎤ ⎡⎤⎡⎤⎡ ⎤
⎢⎥⎢⎥ ⎢⎥⎢⎥⎢ ⎥
⎣⎦⎣⎦ ⎣⎦⎣⎦⎣ ⎦
Найдем характеристическое уравнение системы:
[]
11 1
11 2 1 2 21
221 2
2
2 11 112 12 121
p+L -a
det pI - (A - LC) = = (p + L )(p + a )+ a (a + L )=
a+L p+a
=p+(a+L )p+La+aa+aL;
⎡⎤
⎢⎥
⎣⎦
22
ж
00
Д (p)= p + 2 ω p+ω⋅⋅ .
x
1
x
2
p
a
2
-
-
u
p
a
1
134
Приравнивая коэффициенты при «р» в одинаковой степени найдем
коэффициенты связей наблюдателя:
211 0
2
11212121 0
a+L =2ω
La+aa+aL =ω
⎧
⎨
⎩
;
11 0 2
2
21 0 1 2 2 0 2
1
L=2ω -a ;
1
L= ω -a a -a (2ω -a ) ;
a
⎡
⎤
⎣
⎦
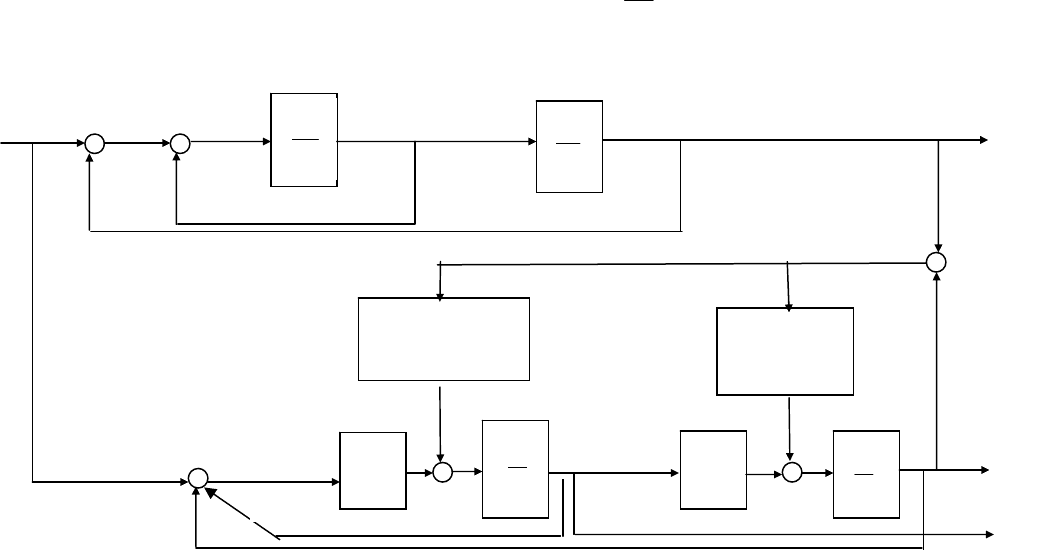
Структурная схема объекта с наблюдателем приведена на рис. 14.4.
Рис. 14.4. Структура наблюдателя с объектом
Связи наблюдателя необходимо вводить на входы интеграторов.
14.2. Редуцированный наблюдатель
Рассмотренный в предыдущей лекции наблюдатель называют
наблюдателем полного порядка. Он оценивает весь вектор
x, несмотря на то,
что компоненты вектора
“y”, входящие в состав “x”, могут быть измерены
непосредственно. Для восстановления лишь тех переменных, которые не
могут быть непосредственно измерены, наблюдатель может быть выполнен
как редуцированный, или наблюдатель пониженного порядка. Все
переменные состояния объекта, составляющие вектор
“x”, можно разделить
на измеряемые, которые образуют вектор
“y”, размерности m, и
неизмеряемые, образующие вектор
w размерности (n-m), т.е. записать:
}
}
m
y
x=
w
n-m
⎡⎤
⎢⎥
⎣⎦
(14.8)
21
L
ˆ
24
x
=x
ˆ
13
x
=x
2
ˆ
x
-
−
x
1
x
2
p
a
2
−
−
u
L
11
p
a
1
a
2
p
1
a
1
p
1
−
−
135
Тогда уравнение
B
u
A
x
x
+=
&
может быть записано в виде:
11 12 1
21 22 2
AA B
yy
=×+×u
AA B
ww
⎡⎤⎡⎤
⎡⎤ ⎡⎤
⎢⎥⎢⎥
⎢⎥ ⎢⎥
⎣⎦ ⎣⎦
⎣⎦⎣⎦
&
&
(14.9)
или, что то же самое:
11 12 1
21 22 2
y=A y+A w+Bu
w= A y+A w+B u
⎫
⎬
⎭
&
&
(14.10)
(14.11)
эти матрицы имеют размерности:
;
11
A
-m×m
;
22
A
-(n-m)×(n-m)
;
12
A
- m × (n - m) ;
21
A
-(n-m)×m
;
1
B
-m×1
2
.
B
-(n-m)×1
На основании второго уравнения (14.11) можно рассматривать часть
системы с выходным вектором
w, для которой входными воздействиями
являются
2
В
u и
21
A
y. Для этой части системы по принципам, изложенным
ранее, строится наблюдатель, на входе которого действуют векторы
2
В
u
и
21
A
y , а также вектор ошибки восстановления через некоторую матрицу L.
Матрица
L в редуцированном наблюдателе играет ту же роль, что и в
наблюдателе полного порядка. Вектор
“w” неизмеряем. Однако он может
быть измерен косвенно через вектор входного воздействия
“u” и
измеряемый вектор
“y” в соответствии с первым уравнением системы
(14.10):
12 11 1
A
w= y- A y-B u.
&
Для получения в определенном масштабе вектора ошибки w
~
надо
умножить вектор восстановленных координат
w
ˆ
слева на матрицу –
А
12
и
определить разность
ˆ
12 12
A
w- A w. После умножения на L ее следует ввести на
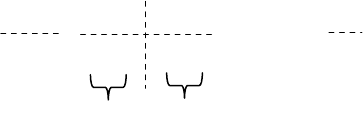
вход наблюдателя. Это поясняет структурная матричная схема (рис.4.4).
Группируя входные каналы с матрицами
2
В
и
1
L
В
,
21
A
и
11
L
A−
, и перенося
сигнал
“p
⋅
y” со входа на выход наблюдающего устройства, что позволяет
избежать операции дифференцирования, можно получить структурную
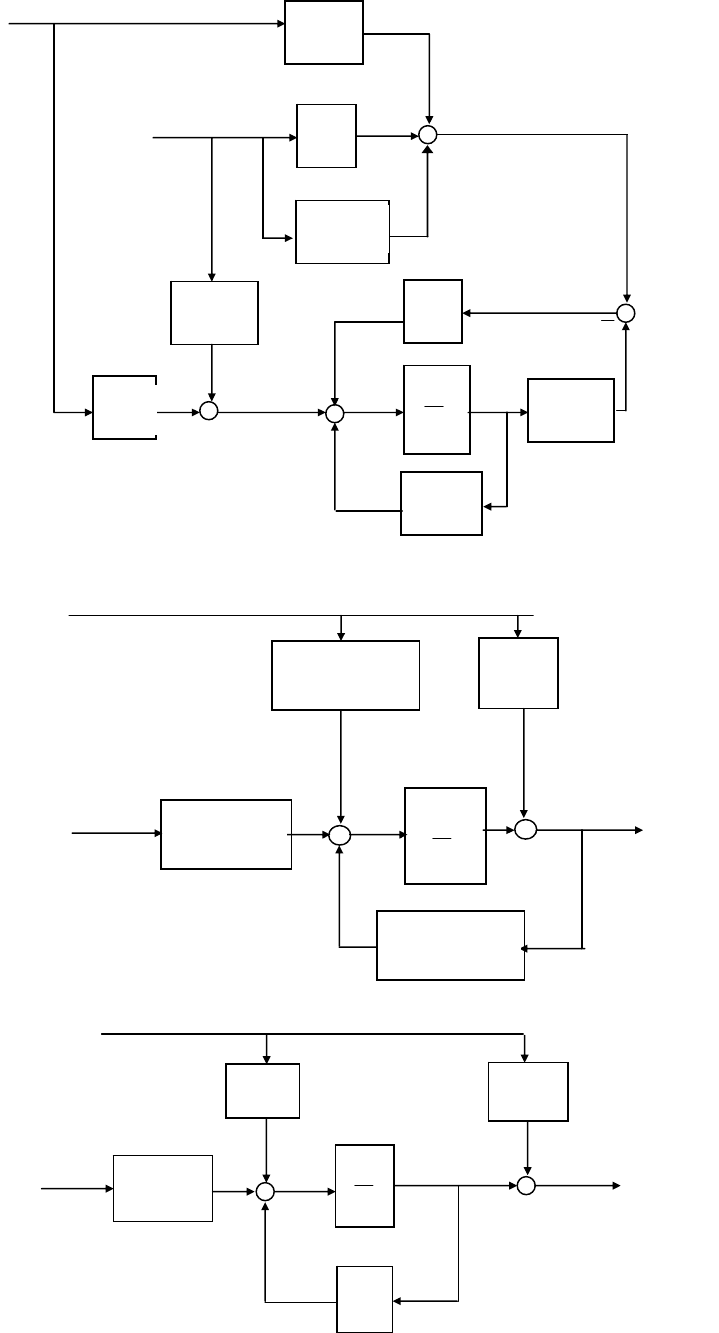
схему на рис. 14.5, а затем, вынося точку суммирования за точку съема,
схему на рис. 14.6, где обозначено:
n-m
m
136
21 11 22 12
22 12
();
;
GA LA A LAL
FA LA
=− + −
=−
Вектор
“z” представляет собой вектор состояния наблюдателя. Он
связан с вектором восстановленных неизмеряемых координат
ˆ
ω и вектором
“y” линейным преобразованием
ˆ
z=w-L×y
.
w
ˆ
y
u
А
21
-LA
11
L
p
I
A
22
-LA
12
B
2
-LB
1
y
w
ˆ
zu
G
L
p
I
F
TB
w
ˆ
y
-В
1
р
-А
11
А
21
В
2
L
p
I
А
22
-А
12
wA
12
wA
ˆ
12
Рис. 14.5
u

137
Учитывая, что в редуцированном наблюдателе полный вектор
восстановленных координат формируется так
ˆ
ˆ
y
x=
w
⎡⎤
⎢⎥
⎣⎦
,
можно записать, что
ˆ
z=Tx
, где
T=[-L I]
. Тогда
21
В
-LB =TB
.
Тем же образом, что и для наблюдателя полного порядка, решается
вопрос выбора динамики или собственных значений матрицы
1222
A
LA
−
,
через выбор матрицы
L.
12
)] ( ).
22 ж
det [pI - (A LA Д p−=
Для схемы на рис. 14.4 уравнение наблюдателя:
ˆ
ˆ
22 12 21 11 2 1
w = (A - LA )w+(A - LA )y + Ly +(B - LB )u
&&
.
Пример 2. Построить наблюдатель для восстановления переменной х
2
в
объекте, приведенном ранее.
111
22222
x
0a x 0
=×+u
x-a-axa
⎡⎤⎡ ⎤⎡⎤⎡⎤
⎢⎥⎢ ⎥⎢⎥⎢⎥
⎣⎦⎣ ⎦⎣⎦⎣⎦
&
&
;
[]
1
1
2
x
y= 1 0 × x
x
⎡⎤
=
⎢⎥
⎣⎦
;
22 12 2 11 1 2 11 1
A
-LA =[-a ]-[l ]×a =-(a +l a )
;
[
]
22 12 2 11 1 0 ж
det pI - (A - LA ) = p + a +l a = p + w = Д (p).
02111
ω =a +l a
02
11
1
ω -a
l=
a
;
21 11 2 11 2
0;
A
LA a l a−=−−⋅=−
21211 2
0.
B
LB a l a
−
=−⋅=
Схема наблюдателя приведена на рис. 14.8.
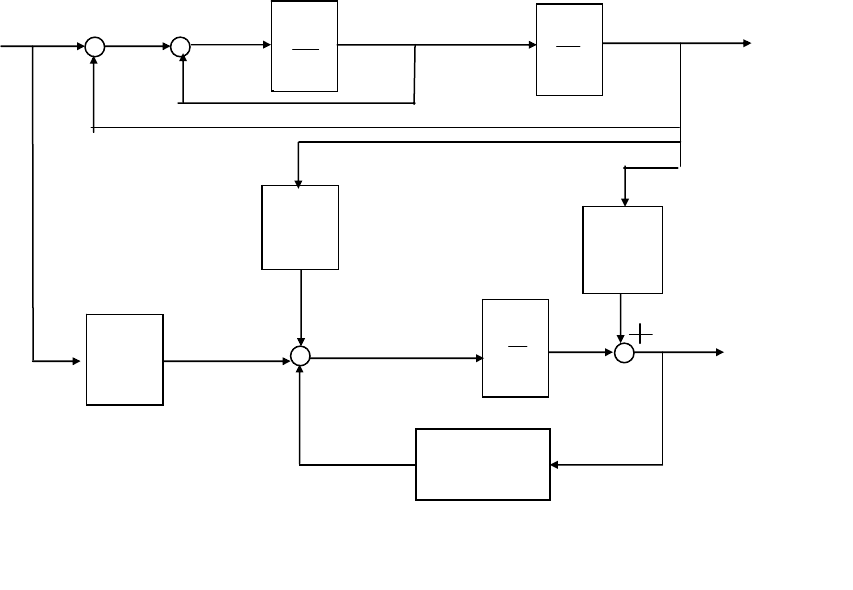
138
С помощью рассмотренных наблюдателей дополнительно можно
решать и другие задачи, например.
1. Оценивать возмущения, приложенные к объекту (для этого
необходимо в уравнения состояния объекта ввести возмущения как одну из
координат).
2. Оценивать изменяющиеся параметры системы
k
i
, T
i
и на этой основе
строить адаптивные системы.
2
ˆ
x
z
-
x
2
p
a
2
-
-
u
2
a
p
1
x
1
=y
p
a
1
11
l
1112
ala
+
Рис. 14.8
2
a
139
Оценки координат можно использовать для построения модального
регулятора.
140
15. ОСОБЕННОСТИ ДИНАМИКИ СИСТЕМЫ, ЗАМКНУТОЙ ЧЕРЕЗ
НАБЛЮДАТЕЛЬ
Рассмотрим систему с модальным регулятором, где обратные связи
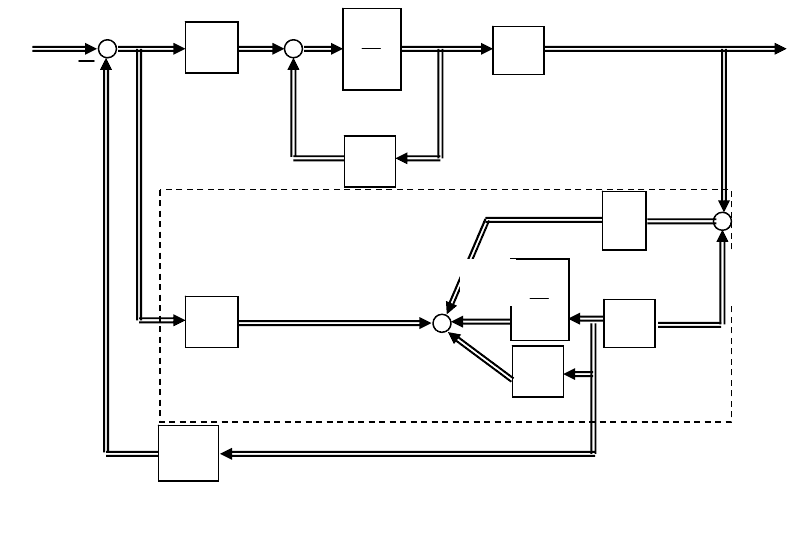
замкнуты по переменным состояния, выработанным наблюдателем (рис.
15.1).
Система описывается уравнением:
x
=Ax+Bu
&
. (15.1)
Наблюдателю соответствует уравнение:
ˆ
ˆ
x
=(A-LC)x+Bu+Ly
&
.
(15.2)
x
&
Р
ис.15.1.Система с модальным
р
ег
у
лято
р
ом и наблюдателем
x
ˆ
y
x
u
V
B
p
I
К
B
x
ˆ
p
I
наблюдатель
ˆ
x
&
ˆ
y
141
Модальному регулятору соответствует закон управления:
ˆ
u=V -Kx. (15.3)
Допустим, что
V=0 (для простоты). Подставим (15.3) в (15.1) и (15.2) и
объединим выражения (15.1) и (15.2) тогда получим:
ˆ
ˆ
ˆ
x= Ax-BKx
x
= (A - LC - BK)x + LCx
⎧
⎨
⎩
&
&
; (15.4)
здесь учтено, что
Ly=LCx.
142
ˆ
ˆ
x
A
-BK x
=×
L
CA-LC-BK x
x
⎡⎤
⎡
⎤⎡⎤
⎢⎥
⎢
⎥⎢⎥
⎣
⎦⎣⎦
⎣⎦
&
&
(15.5)
Это уравнение системы с наблюдателем и модальным регулятором.
Перейдем от переменных
ˆ
(x,x)
к переменным (x,е), где
ˆ
e= x- x
.
Первое уравнение получим путем добавления и вычитания слагаемого
B
Kx к
первому уравнению системы (15.4), второе уравнение получим, вычитая из
(15.1) уравнение (15.2).
ˆˆ
ˆ
ˆˆˆ
x = Ax - BKx + BKx - BKx = (A - BK)x + BK(x - x)
x-x=Ax+Bu-(A-LC)x-Bu-Ly=Ax-(A-LC)x-LCx=(
A
-LC)(x-x).
⎧
⎨
⎩
&
&&
Запишем в векторно-матричной форме:
x
A-BK BK x
=×
e0A-LCe
⎡
⎤⎡ ⎤⎡⎤
⎢
⎥⎢ ⎥⎢⎥
⎣
⎦⎣ ⎦⎣⎦
&
&
(15.6)
Матрица последней системы треугольная, поэтому характеристический
полином замкнутой системы
d(p) удовлетворяет уравнению:
d(p)= b(p) c(p),
⋅
