Смольников А.П. Теория автоматического управления
Подождите немного. Документ загружается.

213
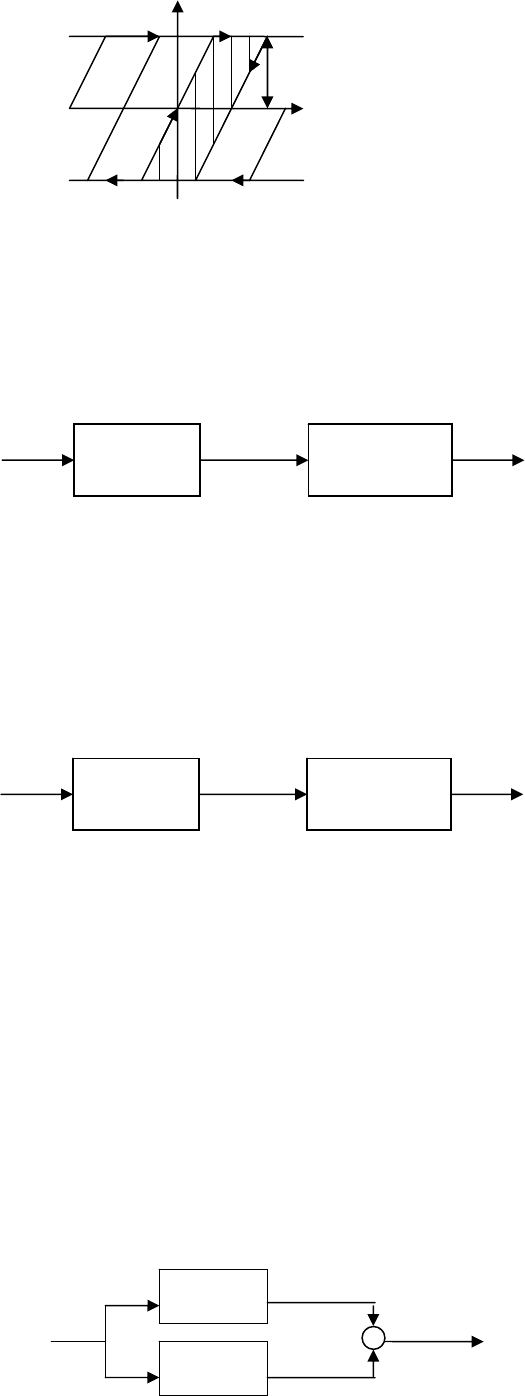
26.5. Основные виды соединений нелинейных звеньев
1) Последовательное соединение.
Сигнал “
y” на выходе из системы
y=F
2
(x
2
)=F
2
[F
1
(x
1
)]=F
2
[F
1
(x)] (26.1)
Если звенья поменять местами, то получим
На выходе системы
)]([)([)(
2122111
xFFxFFxFy
=
== (26.2)
Пусть в обоих случаях входные сигналы “
x” равны, тогда из (26.1) и
(26.2) следует, что выходные сигналы не равны.
Следовательно, при последовательном соединении нелинейных звеньев
не выполняется
принцип коммутативности, поэтому НЗ нельзя менять
местами.
2) Параллельное соединение
F
1
(x
1
)
F
2
(x
2
)
x
2
y
2
y
x
y
1
X
1
X
2
С
x
1
Рис. 26.13
F
1
(x
1
) F
2
(x
2
)
x=x
1
y
1
=x
2
y
2
=y
Рис. 26.14
x=x
2
F
2
(x
2
) F
1
(x
1
)
y
2
=x
1
y
1
=y
Рис. 26.15
214
yy
1
yy
1
x
2
x
x = x
1
y
x = x
1
= x
2
y = y
1
+ y
2
= F(x
1
) + F(x
2
)
3) Встречно– параллельное соединение звеньев.
y = F
1
( x
1
) = F
1
( x – y
2
) = F
1
[ x - F
2
(y)]
Выходная величина выражена в этом случае неявно.
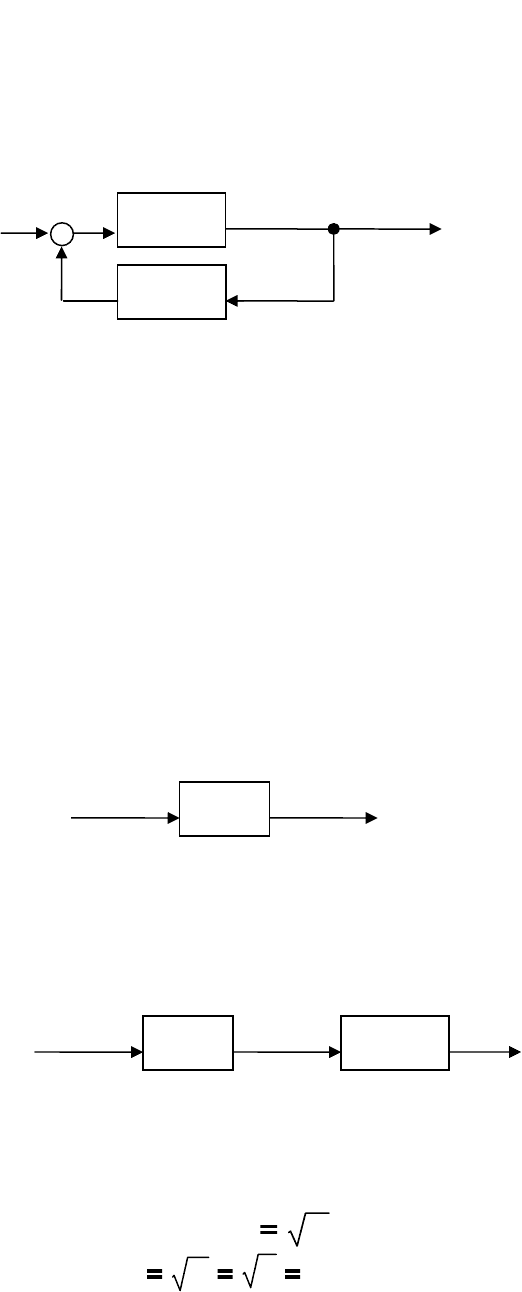
26.6. Способы нейтрализации нелинейных звеньев
Нейтрализация нелинейных звеньев применяется для того, чтобы
исключить нелинейные звенья и приблизить систему к линейному виду.
Существует 2 способа нейтрализации
I) Последовательное включение звеньев
Пусть в НЗ «y» зависит от «x» нелинейно.
Для того чтобы сделать связь между
y и x линейной можно
последовательно с этим НЗ включить другое НЗ с
обратной
характеристикой.
y = F
-1
(y
1
) = F
-1
[ F(x
1
)] = x
Пример.
Пусть y
1
= x
2
, а
тогда
Это свойство используется для преобразования структурных схем
Рис. 26.16
y
2
x
1
F
1
(x
1
)
F
2
(x
2
)
x
y
1
= y
x
2
-
Рис. 26.17
F(x
1
)
x = x
1
y
1
Рис. 26.18
F(x
1
)
F
-1
(y
1
)
y
1
=x
2
Рис. 26.19
215
y
1
y
y
1
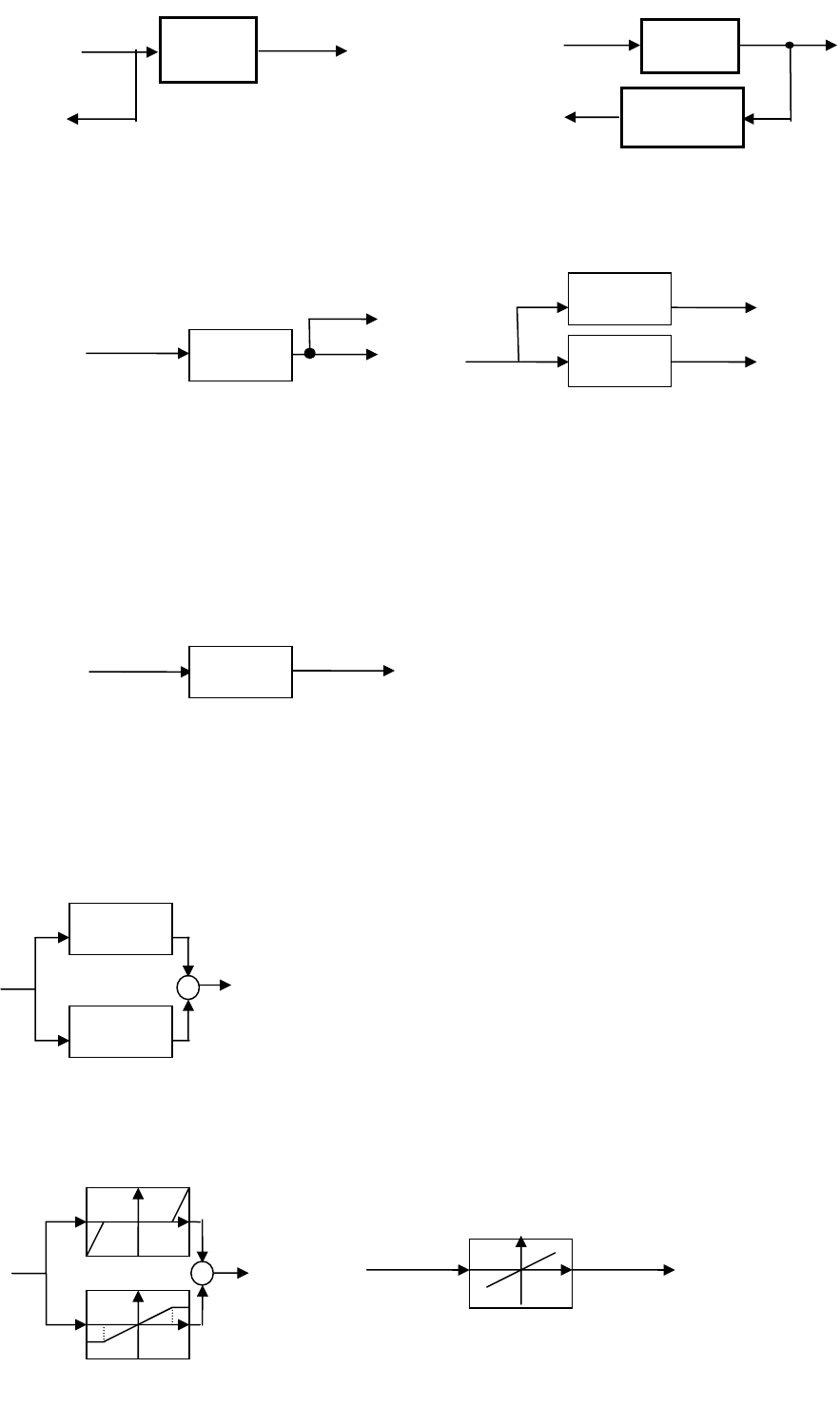
а) Перенос узла разветвления с входа НЗ на выход
б) Перенос узла разветвления с выхода НЗ на вход.
2) Параллельное подключение звеньев.
Пусть имеем НЗ
Чтобы нейтрализовать
F
1,
необходимо подключить такое звено с
нелинейной функцией
F
2
,чтобы выполнялось условие y = F
1
(x) + F
2
(x) = x.
В этом случае характеристика двух звеньев будет линейной. НЗ, которые
удовлетворяют этому условию, называются
взаимодополнительными.
Пример. Пусть имеем звено типа “зона
нечувствительности”. Чтобы нейтрализовать
нелинейность необходимо включить параллельно
звено типа “ограничение”, тогда получим линейную
результирующую характеристику
x
1
y
1
x
1
1
()
F
x
x
1
y
1
x
1
1
()Fx
1
1
()
F
y
−
Рис. 26.20
а
б
F(x
1
)
x
1
y
1
y
1
F
1
(x
1
)
x
1
y
1
F
1
(x
1
)
Рис. 26.21
а
б
F
1
(x
1
)
x
1
Рис. 26.22
F
1
(x
1
)
x
F
2
(x
2
)
y
1
y
2
y
+
Рис. 26.23
x
y
1
y
2
-b
b
-b
b
y
+
x
y
Рис 26
24

216
27. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ НА ОСНОВЕ
МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ НЕЛИНЕЙНОСТЕЙ
27.1. Метод гармонической линеаризации нелинейностей
Из-за трудностей описания нелинейные системы обычно сводят, если
это возможно к линейным.
Ранее была рассмотрена линеаризация в близи рабочей точки, однако
она требует непрерывных функций и малых отключений это – линеаризация
во
временной области.
Гармонической линеаризация – это линеаризация в частотной
области
. При этом нелинейный элемент заменяется линейным, но
эквивалентным исходному только относительно основной составляющей
колебаний. Гармоническая линеаризация может успешно применяться в
случае разрывных кривых и значительных отклонений переменных.
Этот метод нашел широкое применение для определения
автоколебательных процессов и устойчивости нелинейных систем.
Является мощным методом исследования, так как применяется для
систем любого
порядка.
Единственное ограничение: необходимо, чтобы линейная часть
системы обладала хорошими фильтрующими свойствами, то есть подавляла
все гармоники, кроме первой.
Пусть имеем НЗ, которое описывается уравнением:
211
(, )
x
Fx px=
(27.1)
а
б
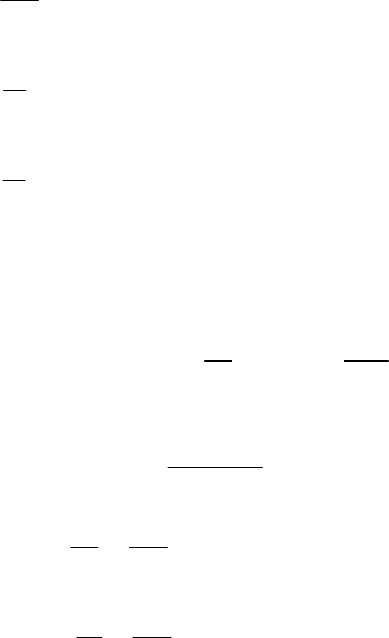
217
где x
1
– сигнал на входе НЗ;
x
2
– сигнал на выходе НЗ;
p – оператор дифференцирования.
Пусть сигнал на входе НЗ
1
sin ,
x
at
ψ
ψω
=⋅ = (27.2)
Тогда
1
cospx a
ω
ψ
=⋅⋅ (27.3)
Выходной сигнал НЗ, соответствующий уравнению (27.1), может быть
разложен в ряд Фурье
2011
( ) ( sin ) sin cosxt Fa a a b высшие гармоники
ψ
ψψ
=⋅ =+⋅ +⋅ + (27.4)
где
2
0
0
1
(sin, cos) ,
2
aFaad
π
ψ
ωψψ
π
=⋅
∫
2
1
0
1
( sin , cos ) sin ,aFaa d
π
ψ
ωψ ψψ
π
=⋅
∫
(27.5)
2
1
0
1
( sin , cos ) cos ,bFaa d
π
ψ
ωψ ψψ
π
=⋅
∫
Пусть
a
0
= 0, то есть постоянная составляющая равна 0.
Из (27.2) имеем
11
sin , cos .
x
px
aa
ψψ
ω
== (27.6)
Тогда (27.4) можно записать следующем образом :
21 1
(, )
(, ) ..
qa
xqa x pxвг
ω
ω
ω
′
=+ +. (27.7)
2
1
0
1
( , ) ( sin , cos ) sin ,
a
qa Fa a d
aa
π
ω
ψω ψ ψψ
π
== ⋅
∫
2
1
0
1
(, ) ( sin , cos )cos ,
b
qa Fa a d
aa
π
ω
ψω ψ ψψ
π
′
== ⋅
∫
где
q и q` – коэффициенты гармонической линеаризации.
Таким образом, при
1
sinxa
ψ
=
⋅ (27.1) заменяем уравнением (27.7),
которое с точностью до высших гармоник аналогично линейному.
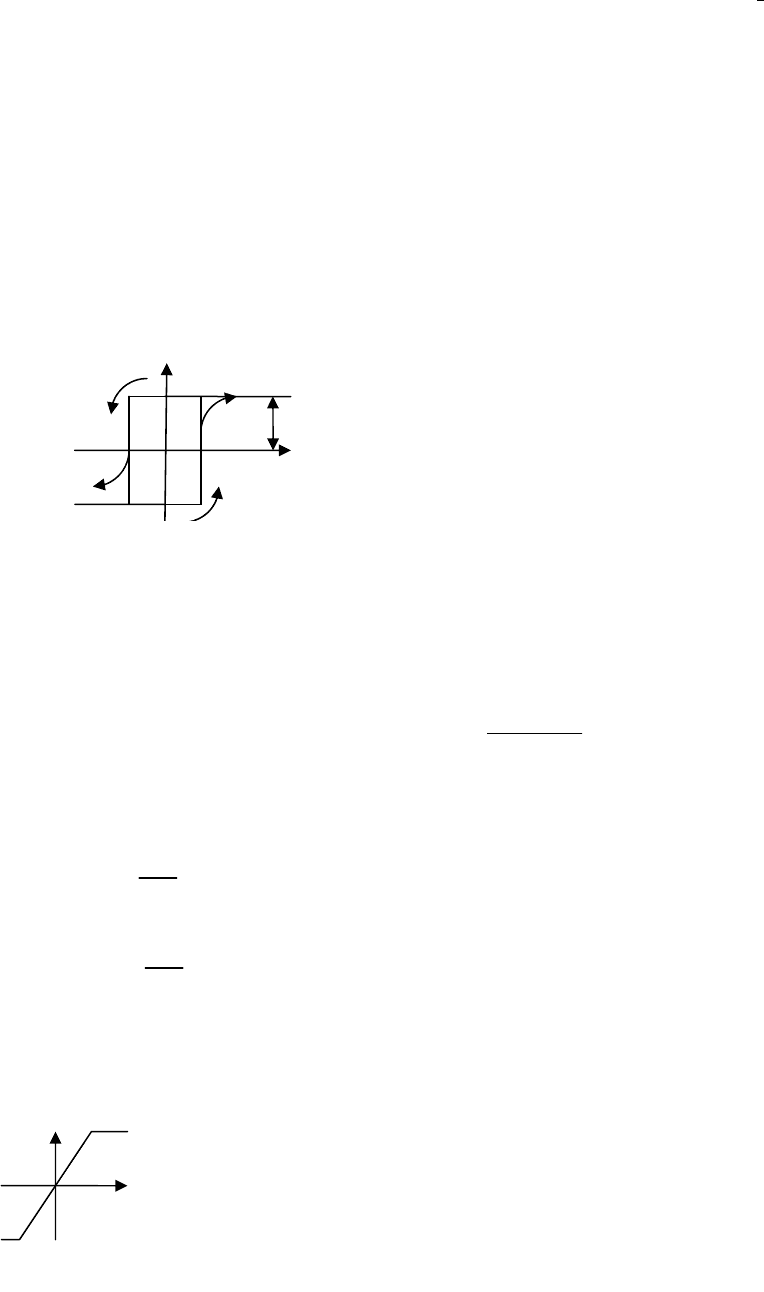
218
Эта операция называется гармонической линеаризацией.
Если на входе НЗ действует сигнал с постоянной амплитудой и
частотой, то
q и q` являются постоянными. Таким образом, коэффициенты
линеаризации будут постоянны при постоянных значениях
a и ω, то есть в
случае периодического процесса. Однако в общем случае это условие не
выполняется и коэффициенты
q и q` будут переменными и зависят от
амплитуды входного сигнала и его частоты.
Рассмотрим гармоническую линеаризацию для простой нелинейной
зависимости
21
()
x
Fx
=
Здесь возможны два случая.
1. Нелинейная характеристика имеет петлю гистерезиса.
В этом случае выходной сигнал будет зависеть от знака производной
входного сигнала.
Тогда, если на вход действует сигнал
1
sin ,
x
at
ψ
ψω
=⋅ = (27.8)
то
211
(, )
() ( , )
qa
x
tqa x px
ω
ω
ω
′
=+
, (27.9)
Высшими гармониками ряда в выходном сигнале пренебрегают.
Коэффициенты гармонической линеаризации
2
0
1
( , ) ( sin ) sin ,qa Fa d
a
π
ω
ψψψ
π
=⋅
∫
2
0
1
(, ) ( sin )cos ,qa Fa d
a
π
ω
ψψψ
π
′
=⋅
∫
2. Нелинейная характеристика не имеет гистерезисной петли.
В этом случае при x = x
1
= a sinψ, dx = a cosψ dψ.
В интеграле заменим переменную
ψ на x.
Новые пределы интегрирования для переменой
x:
ψ = 0 => x = 0,
ψ= 2π => x = 0
x
1
x
2
b
x
1
c
-b
x
2
Рис. 27.1
Рис. 27.2
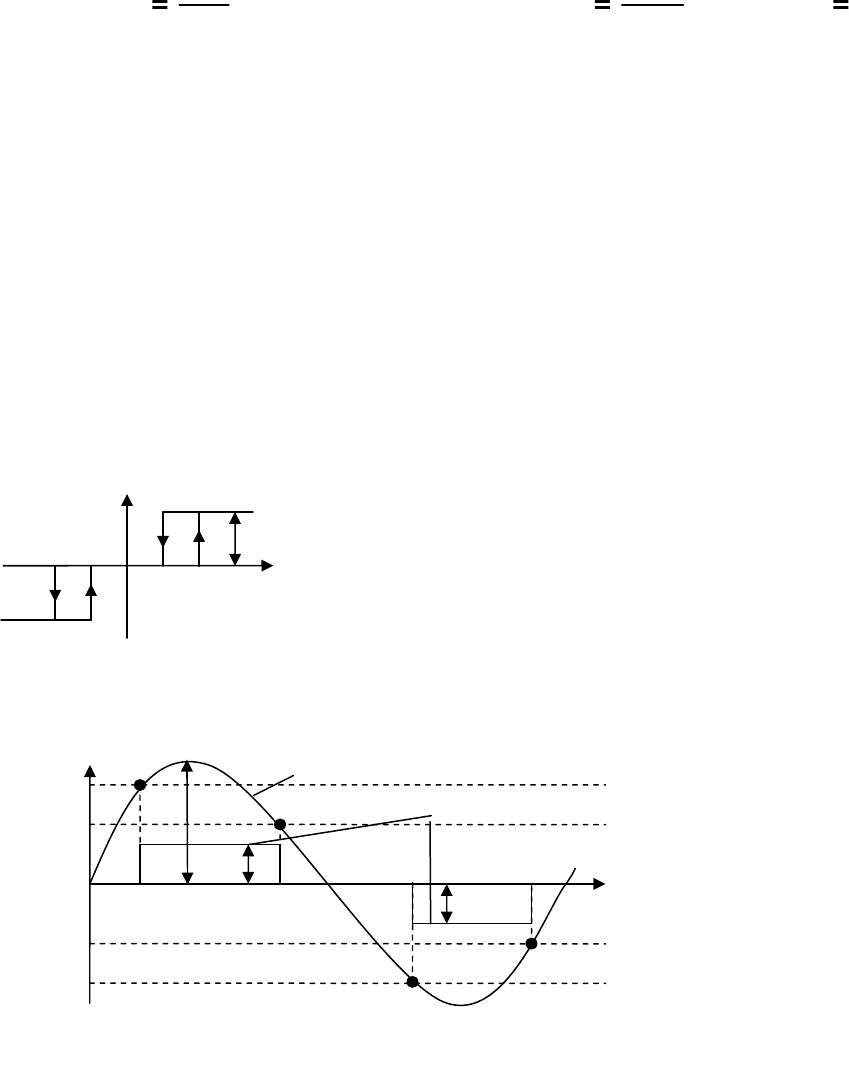
219
q' a ω,
()
1
π a⋅
0
2
π⋅
ψF a sin ψ
()
⋅
()
cos ψ
()
⋅
⌠
⎮
⌡
d⋅
1
π a
2
⋅
0
0
xFx()
⌠
⎮
⌡
d⋅ 0
,
Таким образом, получим
.0)(,0)( =
′
≠ aqaq
Следовательно, при отсутствии гистерезисной петли уравнение имеет
вид
x
2
= q(a) x
1
27.2. Коэффициенты гармонической линеаризации релейных
звеньев
Рассмотрим НЗ типа трехпозиционное
реле с гистерезисом. Пусть на вход звена
подается гармонический сигнал:
x
1
=a sin ωt.
Если амплитуда входного сигнала a < b,
то выходная величина
x
2
равна 0 и движения в
системе не будет. Если
a > b , то переключение
реле происходит в точках
A, B, C ,D.
Из рис. 27.4 можно определить углы:
ψ
1
= arcsin (b/a) ψ
2
= π – arcsin(mb/a) ψ
3
= π + ψ
1
ψ
4
= π + ψ
2
Для симметричных нелинейностей справедливо:
∫∫∫∫∫∫∫
=++==
12
12
2
1
0
2
000
;2
ψψ
ψ
π
ψ
ψ
ψ
πππ
Тогда коэффициенты линеаризации
B
C
D
b
mb
-b
-mb
a
-C
x
2
2π
π
Ψ
1
Ψ
2
Ψ
3
Ψ
4
ψ=ωt
Входная величина- x
1
A
C
x
2
x
1
C
b
mb
-b
-mb
-1 ≤ m ≤ 1
Рис. 27.3
Рис. 27.4
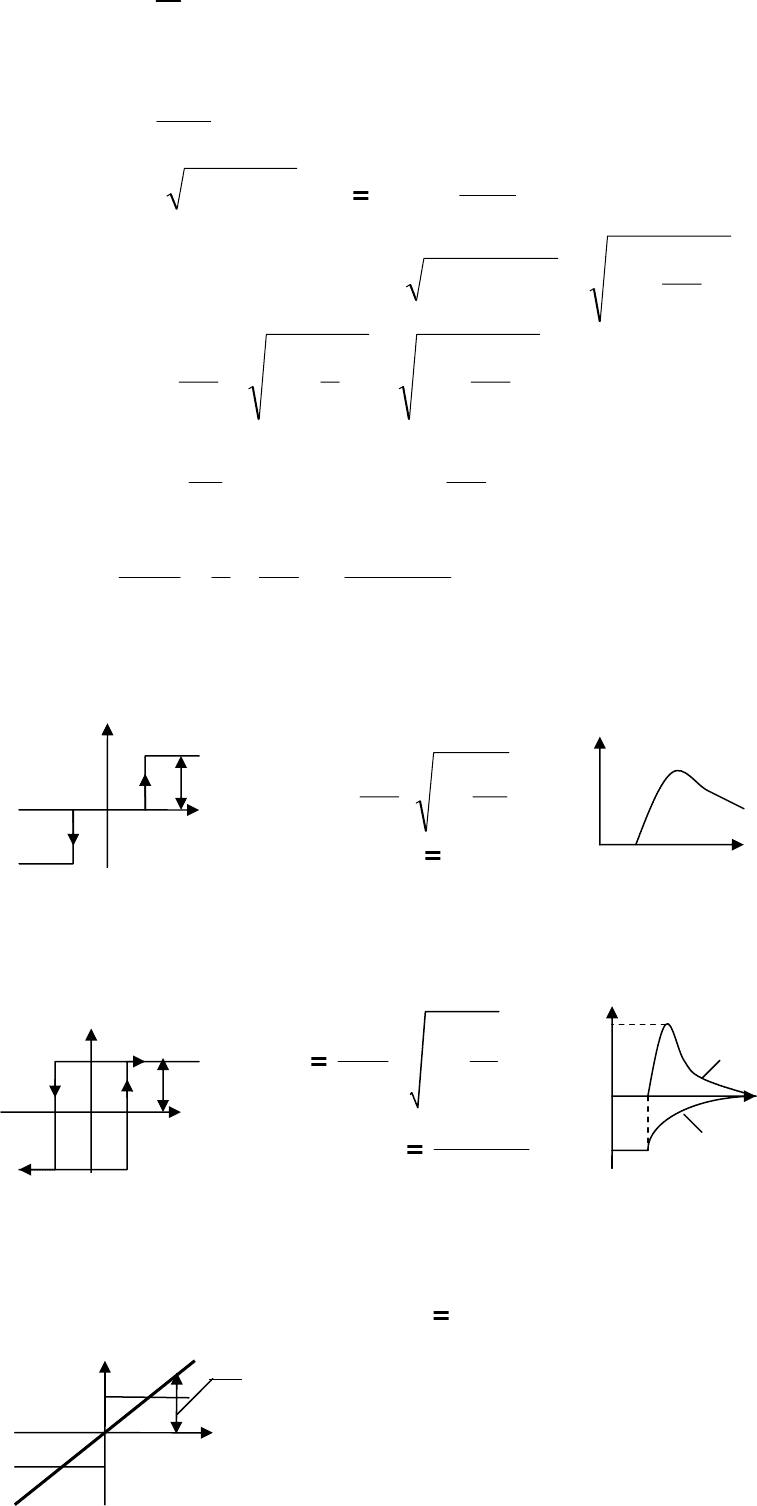
220
a
g(a)
b
q(a)
q`(a)
b
2
1
2
() sin( )
a
qa C d
ψ
π
ψ
ψ
ψ
=⋅
∫
,
где С – амплитуда сигнала на выходе НЗ,
)cos(cos
2
)(
21
ψψ
π
−⋅
⋅
=
a
C
aq ,
ψψ
2
sin1cos −= ,
ψ'
2
arcsin
mb
⋅
a
⎛
⎜
⎝
⎞
⎟
⎠
90
0
<
,
2
2
2
22
1`sin1)`cos(cos
⎟
⎠
⎞
⎜
⎝
⎛
−=−=−−=−
a
mb
ψψπψ
,
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−+
⎟
⎠
⎞
⎜
⎝
⎛
−⋅=
22
11
2
)(
a
mb
a
b
a
C
aq
π
,
)1(
22
)sin(sin
2
cos
2
)`(
2
21
2
1
m
a
bC
a
mb
a
b
a
C
a
C
dC
a
аq
−⋅
⋅⋅−
=
⎟
⎠
⎞
⎜
⎝
⎛
−⋅
−
=
=−⋅−=⋅⋅=
∫
π
π
ψψ
π
ψψ
π
ψ
ψ
Частные случаи релейных звеньев
1. m = 1 ,то есть характеристика имеет вид
В этом случае
2
2
1
4
)(
a
b
a
C
aq −⋅=
π
q' a() 0
,
2. m = -1
qa()
4c⋅
π
a⋅
1
b
2
a
2
−⋅
q' a()
4
−
c
⋅
b
⋅
π a
2
⋅
3.
b = 0
q' a() 0
.
-b
b
С
x
1
x
2
-b
b
С
x
1
x
2
С
x
1
x
2
x
1
=
a
4С
π
С
Рис. 27.5
Рис. 27.6
Рис. 27.8
Рис. 27.7

221
a
q(a)
qa()
4c
⋅
π a⋅
Гармоническая линеаризация означает замену ломаной линии
некоторой прямой
π
π
С
xтоaxеслиx
a
С 4
,;
4
x
2112
==⋅=
.
Причем наклон зависит от амплитуды входного сигнала. Чем больше
амплитуда входного сигнала, тем более полого располагается прямая, то есть
коэффициент
q(a) уменьшается с ростом амплитуды входного сигнала.
Заменив нелинейное уравнение некоторым линейным, можно анализировать
процессы, происходящие в нелинейной системе.
На основе гармонической линеаризации нелинейностей разработано
несколько методов. Все они приближенные, так как при этом пренебрегают
высшими гармониками в выходном сигнале нелинейного элемента.
27.3. Метод гармонического баланса
Метод разработан Гольдфарбом и относится к числу приближенных
методов исследования нелинейных систем. В основе лежит принцип
гармонической линеаризации.
Пусть нелинейная система состоит из нелинейного звена,
описываемого уравнением
21
()
x
Fx
=
(27.10)
и линейной части с передаточной функцией
W
л
(p), тогда получим
структурную схему
Допустим, что в системе существуют автоколебания, то есть
1
sin
п
x
at
ω
=
⋅ (27.11)
Тогда сигнал на выходе НЗ может быть представлен в виде ряда Фурье
211
( ) ( sin ) sin cos
ппп
xt Fa t a t b t высшие гармоники
ω
ωω
=⋅ =⋅ +⋅ + (27.12)
где ω
п
- частота автоколебаний в системе.
Рис. 27.9
Рис. 27.10
Х
вх
= 0
X
2
X
1
X
Н.З.
Л.Ч.
Рис. 27.11
222
Пусть линейная часть системы обладает фильтрующими свойствами,
то есть сигнал
x
2
, проходя через линейную часть системы, теряет все высшие
гармоники.
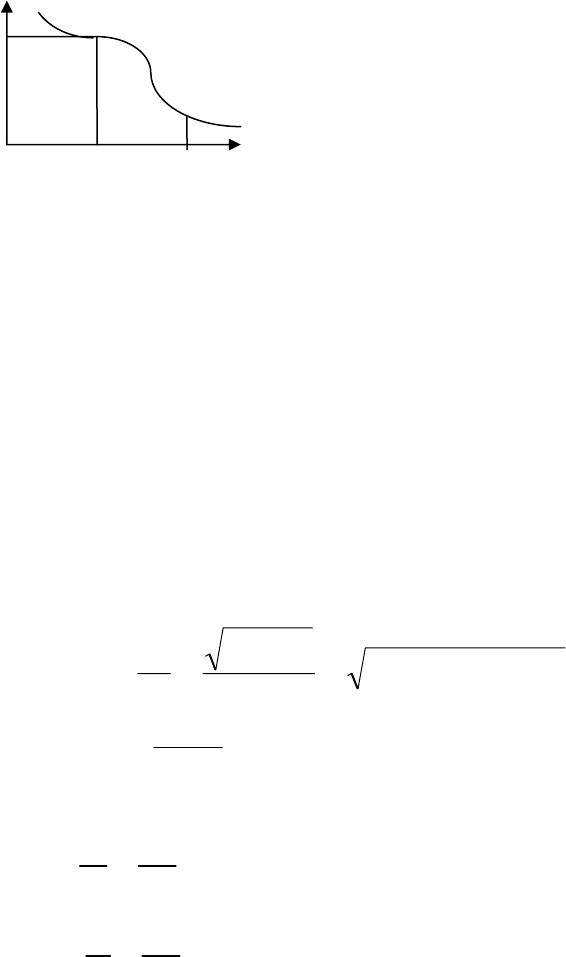
Предположение о том, что линейная часть системы подавляет высшие
гармоники, называется
гипотезой фильтра. АЧХ линейной части часто
имеет вид
Поэтому сигналы с частотой
ω > 3ω
1
существенно ослабляются и ими
можно пренебречь.
С учетом этого уравнение (27.12) можно записать
21 1
( ) sin cos sin( )
ппm пн
xt a t b t b t
ω
ωωϕ
=⋅ +⋅ = +
(27.13)
Сравнивая (27.11) и (27.13) для нелинейного звена, можно увидеть
аналогию с линейным звеном. Поэтому, как и для линейных звеньев,
вводится понятие комплексного коэффициента усиления Н.З.
() () () () ()
Н
j
нн
Wa qa jqa Aae a
ϕ
′
=+ = ⋅
(27.14)
где
22
2
1
2
1
)]`([)()(
αα
α
α
qq
ba
b
аA
m
н
+=
+
==
)(
)`(
)(
α
α
αϕ
q
q
arctg
н
= ,
q(a) и q`(a) – коэффициенты гармонической линеаризации
2
1
0
1
( , ) ( sin , cos ) sin ,
a
qa Fa a d
aa
π
ω
ψω ψ ψψ
π
== ⋅
∫
2
1
0
1
(, ) ( sin , cos )cos ,
b
qa Fa a d
aa
π
ω
ψω ψ ψψ
π
′
== ⋅
∫
где
t
ψ
ω
=⋅
.
Если нелинейная характеристика F(x
1
) не имеет петли гистерезиса, то
q`(a) = 0 и φ
н
(a) = 0.
27.4. Условие гармонического баланса
Для нелинейной системы на рис. 27.11 можно записать.
ω
1-
2
-для нулевого полюса
А
3ω
1
ω
1
Рис. 27.12
