Simon Benninga. Financial Modelling 3-rd edition
Подождите немного. Документ загружается.


778 Chapter 31
AB=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
aa a
aa a
bb
bb
bb
n
pp pn
m
m
nnm
11 12 1
12
11 1
21 2
1
⎣⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
Then the product of A and B, written AB, is defi ned by the matrix
AB =
== =
==
∑∑ ∑
∑∑
h
n
hh
h
n
hh
h
n
hhm
h
n
ph h
h
n
ab ab ab
ab a
1
11
1
12
1
1
1
1
1
pph hm
b
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
with
ij a b
h
n
ih hj
th
element =
=
∑
1
.
Note that the ij
th
coordinate of AB is the product of the ith row of A
times the jth column of B. For example, if
AB=
−
−
⎡
⎣
⎢
⎤
⎦
⎥
=
−
−
⎡
⎣
⎢
⎤
⎦
⎥
26
93
69 12
52 4
,
then
AB =
−
−−
⎡
⎣
⎢
⎤
⎦
⎥
42 6 48
69 75 120
The order of matrix multiplication is critical. Multiplication of matrices
is not commutative; that is, AB ≠ BA. As the preceding example shows,
the fact that it is possible to multiply A times B does not always imply
that the multiplication BA is even defi ned.
In order to multiply matrices in Excel, we use the array function
MMult:
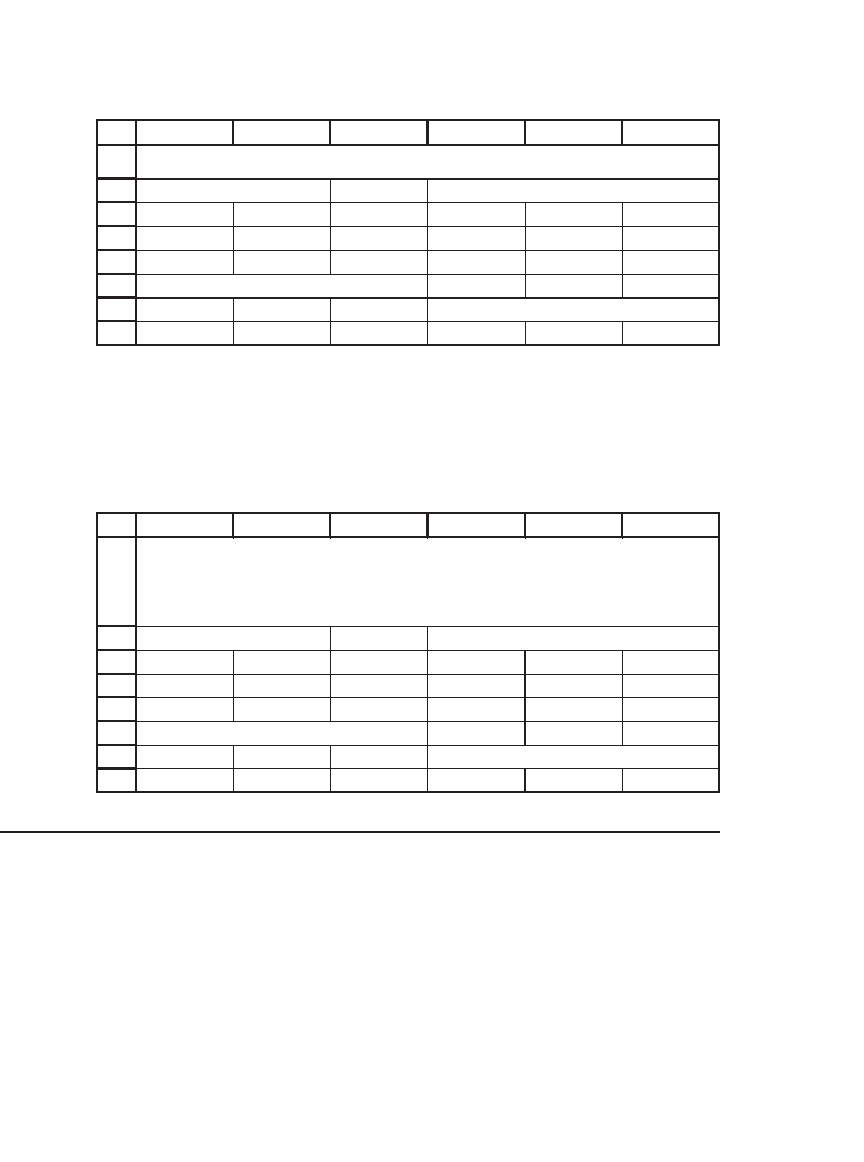
779 Matrices
To multiply two matrices together, the number of columns in the fi rst
matrix must equal the number of rows in the second. Thus we can mul-
tiply A times B, but we cannot multiply B times A. If you try to do so
in Excel, the function MMult will give you an error message:
1
2
3
4
5
6
7
8
ABCDEF
2-7 6 9
03 -52
47 4 -52 <
--
{=MMULT(A3:B4,D3:F4)}
-15 6 12
Product AB
Matrix BMatrix A
MULTIPLYING MATRICES
-12
4
1
2
3
4
5
6
7
8
ABCDEF
2-7
69
03 -52
#VALUE! #VALUE! #VALUE! <
--
{=MMULT(D3:F4,A3:B4)}
#VALUE! #VALUE! #VALUE!
Product BA
Matrix BMatrix A
MATRIX MULTIPLICATION:
Number of c
olumns of first matrix must equal
number of rows of second matrix
-12
4
31.3 Matrix Inverses
A square matrix I is called the identity matrix if all its off-diagonal entries
are 0 and all its diagonal entries are 1. Thus
I =
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
10 00
01 00
00 10
00 01
780 Chapter 31
It is easy to confi rm that multiplying any matrix A by the identity
matrix of the proper dimension leaves that A unchanged. Thus, if I
n
is an
n × n identity matrix and A is an n × m matrix, IA = A. Similarly, if I
m
is
an m × m identity matrix, AI = A.
Now suppose we are given a square matrix A of dimension n. The
n × n matrix A
−1
is called the inverse of A if A
−1
A = AA
−1
= I. The com-
putation of an inverse matrix can be a lot of work; fortunately, however,
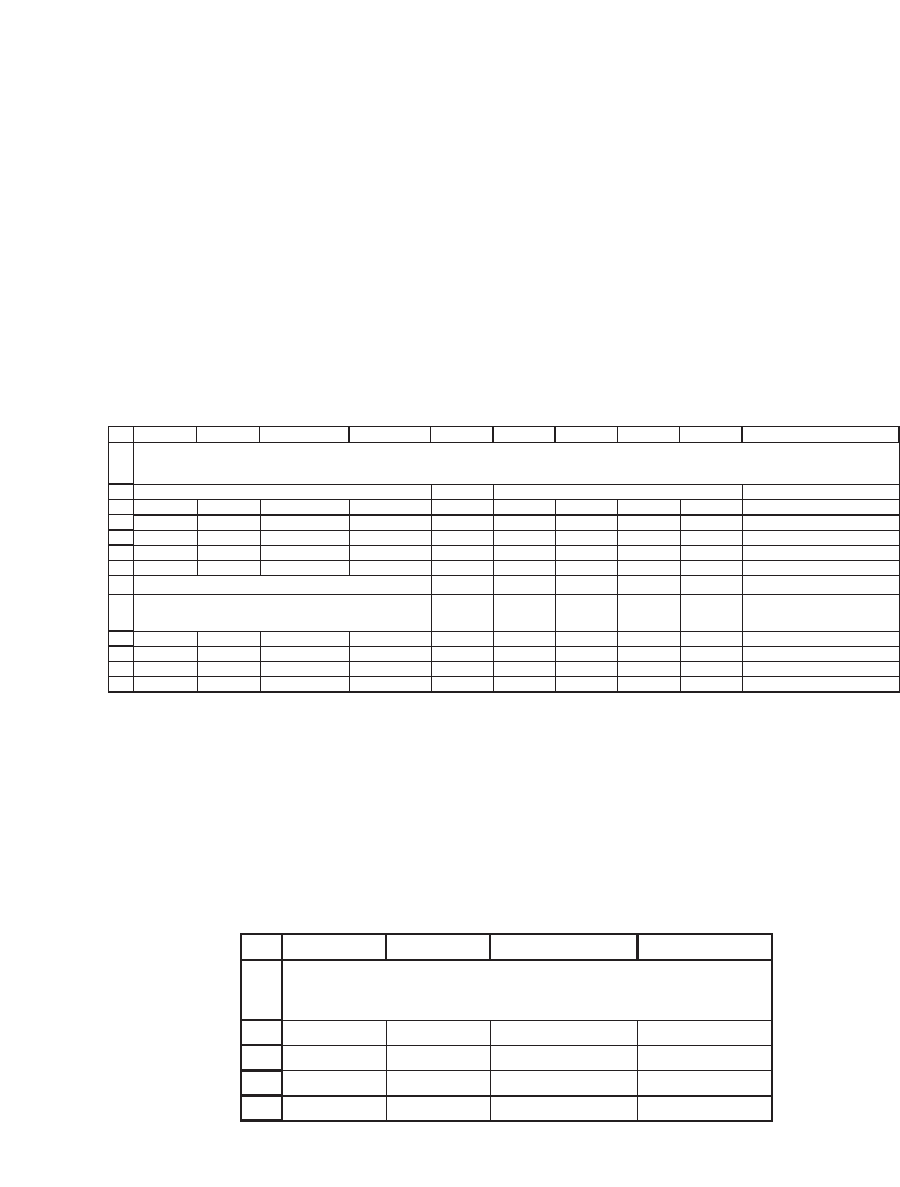
Excel has the array function MInverse which does the calculations
for us. Here’s an example:
1
2
3
4
5
6
7
8
9
10
11
12
13
AB C D EFGHI J
1 -9 16 1 -0.0217 1.8913 0.5362 -1.1449 <
--
{=MINVERSE(A3:D6)}
3 3 2 3 0.0000 -1.0000 -0.1667 0.6667
2 4 0 -2 0.0652 -0.6739 -0.1087 0.4348
5 7 3 4 -0.0217 -0.1087 -0.2971 0.1884
1 1.07E-15 -2.22045E-16 -9.4369E-16
0 1 -1.11022E-16 2.22045E-16
6.94E-18 8.33E-17 1 5.55112E-16
1.39E-17 1.17E-15 -4.44089E-16 1
Verifying the inverse
We multiply A*Inverse A: cells below contain array
function {=MMULT(A3:D6,F3:I6)}
Matrix A
MATRIX INVERSE
Use array function MInverse to compute the inverse of a square matrix
Inverse of A
As the spreadsheet shows, you can use MMult to verify that the product
of the matrix and its inverse indeed give the identity matrix. An expres-
sion like 1.07E-15 means 1.07
*
10
−15
, and such expressions are thus essen-
tially zero; you can use Format|Cells|Number to specify the number of
decimal places and get rid of these ugly expressions:
9
10
11
12
13
AB C D
1.0000 0.0000 0.0000 0.0000
0.0000 1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
We multiply A*Inverse A: cells below contain array
function {=MMULT(A3:D6,F3:I6)}

781 Matrices
A square matrix that has an inverse is called a nonsingular matrix. The
conditions for a matrix to be nonsingular are the following: Consider a
square matrix A of dimension n. It can be shown that A = [a
ij
] is nonsin-
gular if and only if the only solution to the n equations
i
ij i
ax j n
∑
==01, ,...,
is x
i
= 0, i = 1, . . . , n. Matrix inversion is a tricky business. If there exists
a vector X whose components are almost zero and which solves the
above system, then the matrix is ill-conditioned, and it may be very
diffi cult to fi nd an accurate inverse.
31.4 Solving Systems of Simultaneous Linear Equations
A system of n linear equations in m unknown is written as
ax ax ax y
ax ax ax y
ax ax
nn
n
nn
11 1 12 2 1 1
21 1 22 1 2 1 2
11 21
+++=
+++=
++
++=ax y
nn n1
Writing the matrix of coeffi cients as A = [a
ij
], the column vector of
unknowns as X = [x
j
], and the column vector of constants as Y = [y
j
],
we may write this system in matrix notation as AX = Y.
Not every system of linear equations has a solution, and not every
solution of such a system is unique. The system AX = Y always has a
unique solution, however, if the matrix A is square and nonsingular.
In this case the solution is found by premultiplying both sides of the
equation AX = Y by the inverse of A:
since AX Y A AX A Y X A Y=⇒ = ⇒=
−− −11 1
Here is an example. Suppose we want to solve the following 3 × 3
system of equations:
3 4 66 16
33 77
42 3 2 12
12 3
23
12 3
xx x
xx
xx x
++ =
−+=
++ =
782 Chapter 31
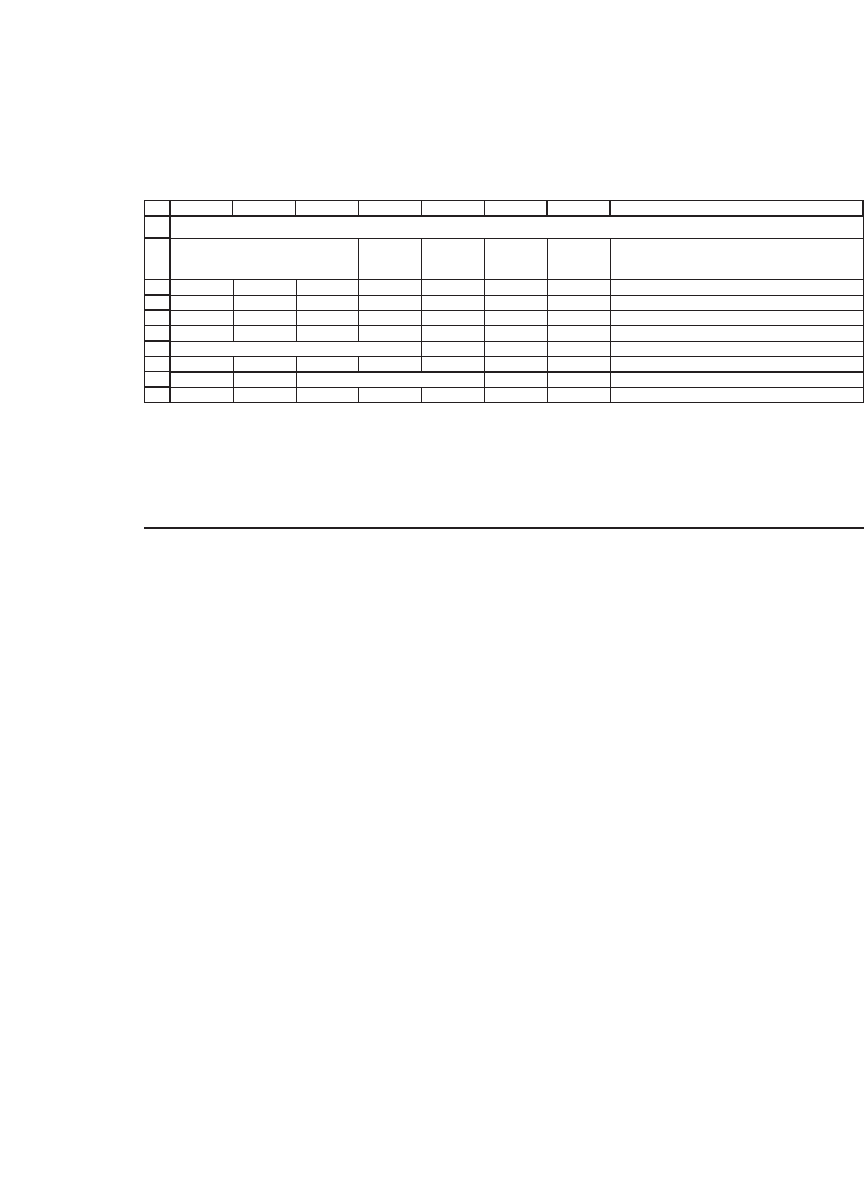
We set this up and solve it in Excel as follows:
1
2
3
4
5
6
7
8
9
10
ABCDEFG H
Column
vector y
Solution
A
-1
Y
3 4 66 16 0.4343
0 -33 1 77 -2.3223 <
--
{=MMULT(MINVERSE(A3:C5),E3:E5)}
42 3 2 12 0.3634
Checking that the solution works
16
77 <-- {=MMULT(A3:C5,G3:G5)}
12
Matrix A of coefficients
SOLVING SIMULTANEOUS EQUATIONS
In cells B8 : B10 we check that the solution indeed solves the system
by multiplying the matrix A times the column vector G3 : G5.
Exercises
1. Use Excel to perform the following matrix operations:
a.
212 6
48 7
10−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
+−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
9
11 2
80 23
17 3
b.
29
50
66
311
232
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎤
⎦
⎥
c.
20 6
48 7
10 9
11 2
80 2
17 3−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
2. Find the inverses of the following matrices:
a.
1289
2530
4427
5216−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
b.
321
613
743
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
c.
20 2 3 3
2102 2
3 2 40 9
32933
−
−
−−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥

783 Matrices
3. Transpose the following matrices using the Excel array function Transpose:
a.
A =−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
321
1541
691
b.
B =− −
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
12345
27 900
3 3 11 12 1
4. Solve the following system of equations by using matrices:
346915
22
3
1
xyzw
xy w
yz w
xyz
+−−=
−+=
++=
+− =
5. Solve the equations AX = Y, where
AYX=
−−
−−
−−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
13 8 3
810 1
3111
20
5
0
1
2
3
,,
x
x
x
⎣⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
6. An ill-conditioned matrix is a matrix that “almost doesn’t have” an inverse. A set
of examples of such matrices are Hilbert matrices. An n-dimensional Hilbert matrix
looks like this:
H
n
n
n
nn n
=
+
+−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
1
1
121
1/2 1/
1/2 1/3 1/(
1/ 1/( 1/(
)
))
a. Calculate the inverses of H
2
, H
3
, and H
8
.
b. Consider the following system of equations:
H
n
n
x
x
x
n
n
n
1
2
1
1
1
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
+++
+++ +
+
1/2 1/
1/2 1/3 1/(
1/ /
)
(nnn+++ −
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
11)) 1/(2
Find the answers to these problems by inspection.
c. Now solve H
n
*
X = Y for n = 2, 8, 14. How do you explain the differences?


32
The Gauss-Seidel Method
32.1 Overview
Many simultaneous equations can be solved by recursive iteration. In
these methods we successively substitute a solution for one equation into
another of the simultaneous equations until a solution is reached. These
Gauss-Seidel methods are often effi cient in solving complicated systems
of equations. In this book we use them in Chapters 3–4 in solving for the
solutions of pro forma fi nancial statements (though we let Excel do the
work!). With some further perspective, this chapter illustrates a wide-
spread and useful computational technique for numerically solving
complex systems.
32.2 A Simple Example
Suppose we are trying to solve the simultaneous linear equations
2310
42
xy
xy
+=
−=
The fi rst equation solves to give x = (10 − 3y)/2, and from the second
equation we obtain y = (x − 2)/4. To use the Gauss-Seidel method, we set
some initial value for y; for example, we can let y = 0. If y = 0, then
x = (10 − 3
*
0)/2 = 5. But if x = 5, then y = (x − 2)/4 = (5 − 2)/4 = 0.75.
If we keep going, we will see that ultimately the values of x and y con-
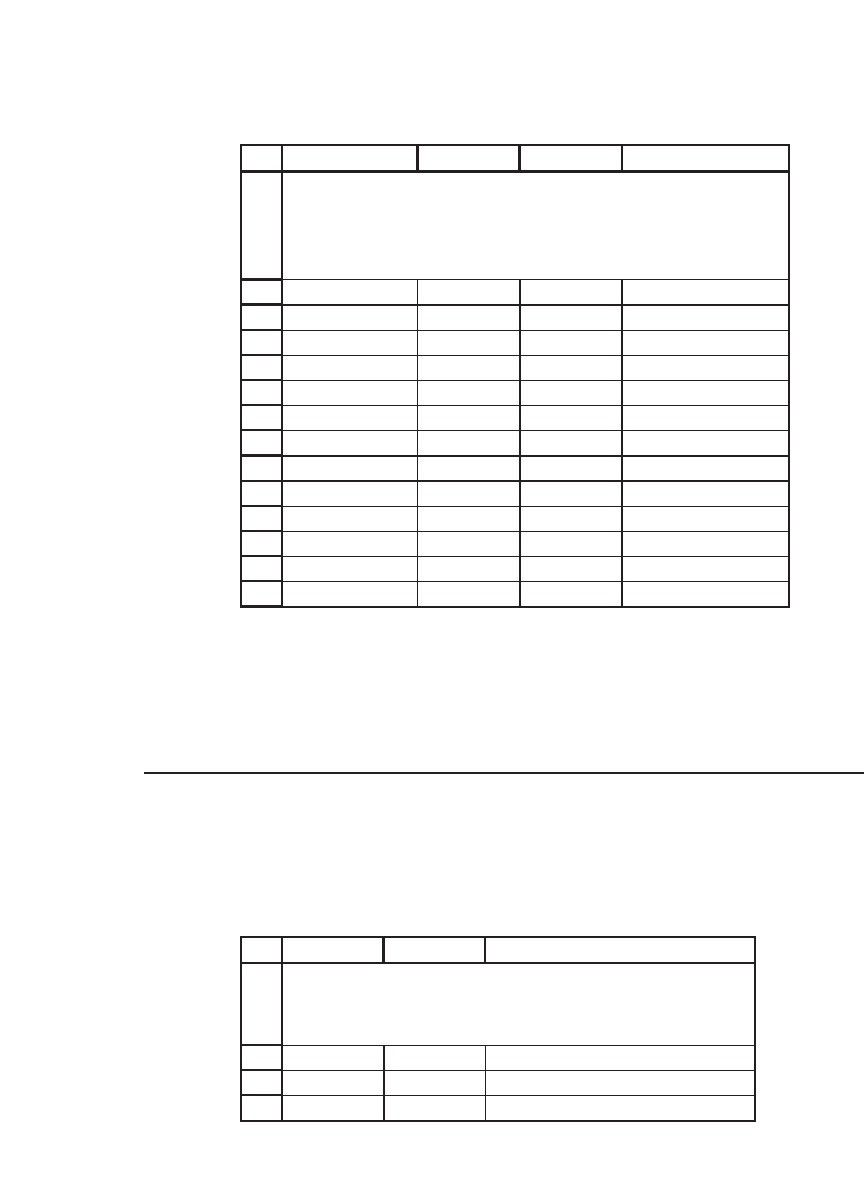
verge to a solution to the equations. Here is the problem, set up as an
Excel table:
786 Chapter 32
As you can see, the values converge. It follows from the way we have
constructed the values that the limits of the two sequences are the solu-
tions to the equations.
32.3 A More Concise Solution
A neater way of solving the same problem is to set up the following
spreadsheet:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
ABC D
yx
05
=(C3-2)/4
--
> 0.75 3.875 <
--
=(10-3*B4)/2
=(C4-2)/4
--
> 0.46875 4.296875 <
--
=(10-3*B5)/2
=(C5-2)/4
--
> 0.574219 4.138672 <
--
=(10-3*B6)/2
0.534668 4.197998
0.5495 4.175751
0.543938 4.184093
0.546023 4.180965
0.545241 4.182138
0.545535 4.181698
0.545425 4.181863
0.545466 4.181801
GAUSS-SEIDEL METHOD:
SOLUTION BY ITERATIVE
SUBSTITUTION
1
2
3
4
AB C
Marker 5
y5<
--
=IF(B2<>0,B2,(B4-2)/4)
x-2.5<
--
=(10-3*B3)/2
GAUSS-SEIDEL METHOD--
SHORTCUT
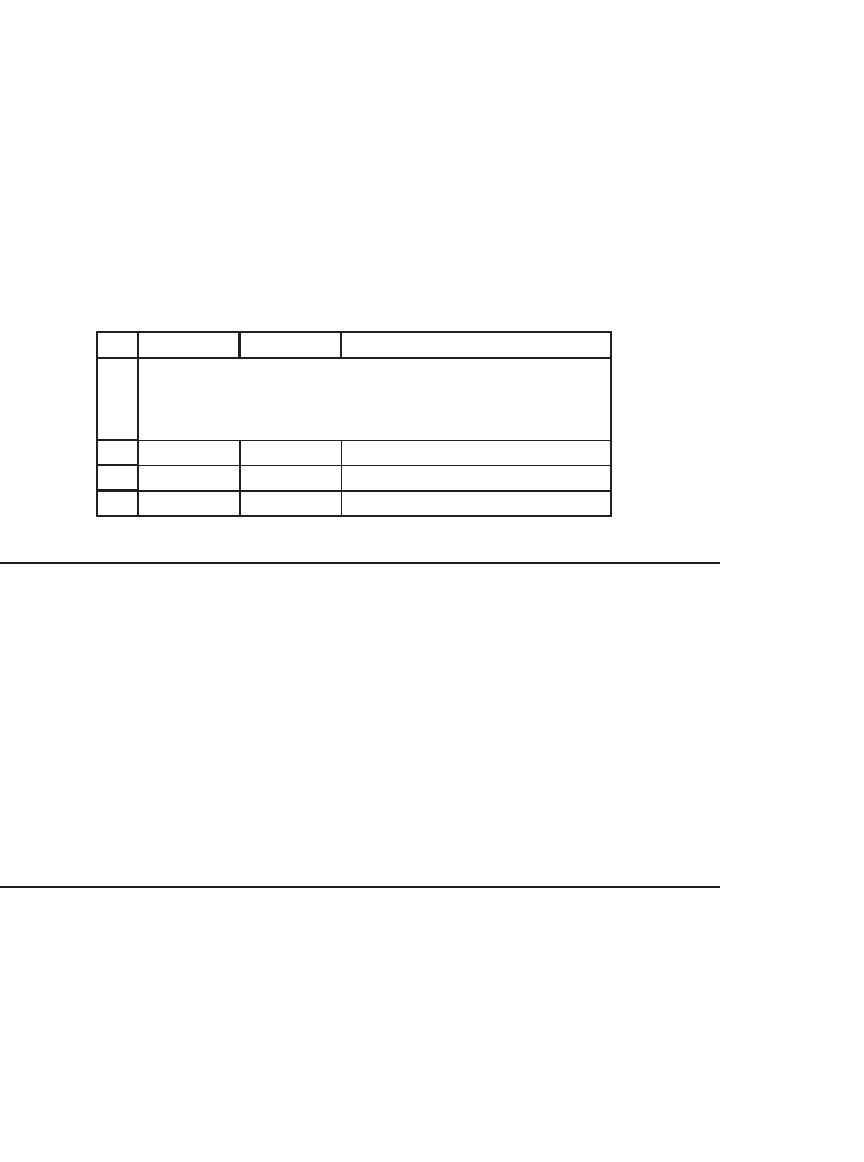
787 The Gauss-Seidel Method
How does this implementation of recursive solutions work? If you set
Marker equal to some nonzero value, c, then you see, as in the spread-
sheet picture, that y = c and x = (10 − 3c)/2. Once you let Marker equal
zero, then the iterative process starts, and if there is a solution, Excel will
fi nd it. To make sure your spreadsheet recalculates, you have to go to the
Tools|Options|Calculation box and click Iteration. See the note on this
topic in section 3.2. Here’s the solution:
1
2
3
4
AB C
Marker 0
y 0.545301 <
--
=IF(B2<>0,B2,(B4-2)/4)
x 4.182049 <
--
=(10-3*B3)/2
GAUSS-SEIDEL METHOD--
SHORTCUT
32.4 Conclusion
The Gauss-Seidel method is a somewhat untidy way of solving simulta-
neous equations. The solution may not always converge, and convergence
may depend on whether x or y is solved for fi rst. The advantage of the
method is that it assures us that what we do in many fi nancial models
makes sense by allowing us to construct a model in which we set up the
relations between the variables without asking how the equations are to
be solved. If we observe convergence, then we have a solution. The
fi nancial statement models of Chapters 3 and 4 are examples of how
powerful the Gauss-Seidel method can be.
Exercises
Solve the following system using the Gauss-Seidel method:
13 8 3 20
810 5
3110
xyz
xyz
xy z
−−=
−+ −=−
−−+ =
Note that in order to get a solution, you may have to hit the F9 (recalculate spreadsheet)
key a few times. You will have gotten a solution if the numbers on the screen stop
changing.
