Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

758 Chapter 29

29.4.3.1 A Faster Version of Method 3

We can make Method 3 much faster by storing all the data in VBA and

only writing the ﬁ nal frequency distribution on the screen:

Sub NormStandardRandom2()

Randomize ‘Initializes the VBA random number

‘generator

Dim distribution(-40 To 40) As Double

Application.ScreenUpdating = False

Range(“E2”) = Time

N = Range(“B2”).Value

For Index = 1 To N

X = Application.NormSInv(Rnd())

If X < -4 Then

distribution(-40) = distribution(-40) + 1

ElseIf X > 4 Then

distribution(40) = distribution(40) + 1

Else: distribution(Int(X / 0.1)) = _

distribution(Int(X / 0.1)) + 1

End If

Next Index

For Index = -40 To 40

Range(“B7”).Cells(Index + 41, 1) = _

distribution(Index) / (2 * N)

Next Index

Range(“E3”) = Time

End Sub

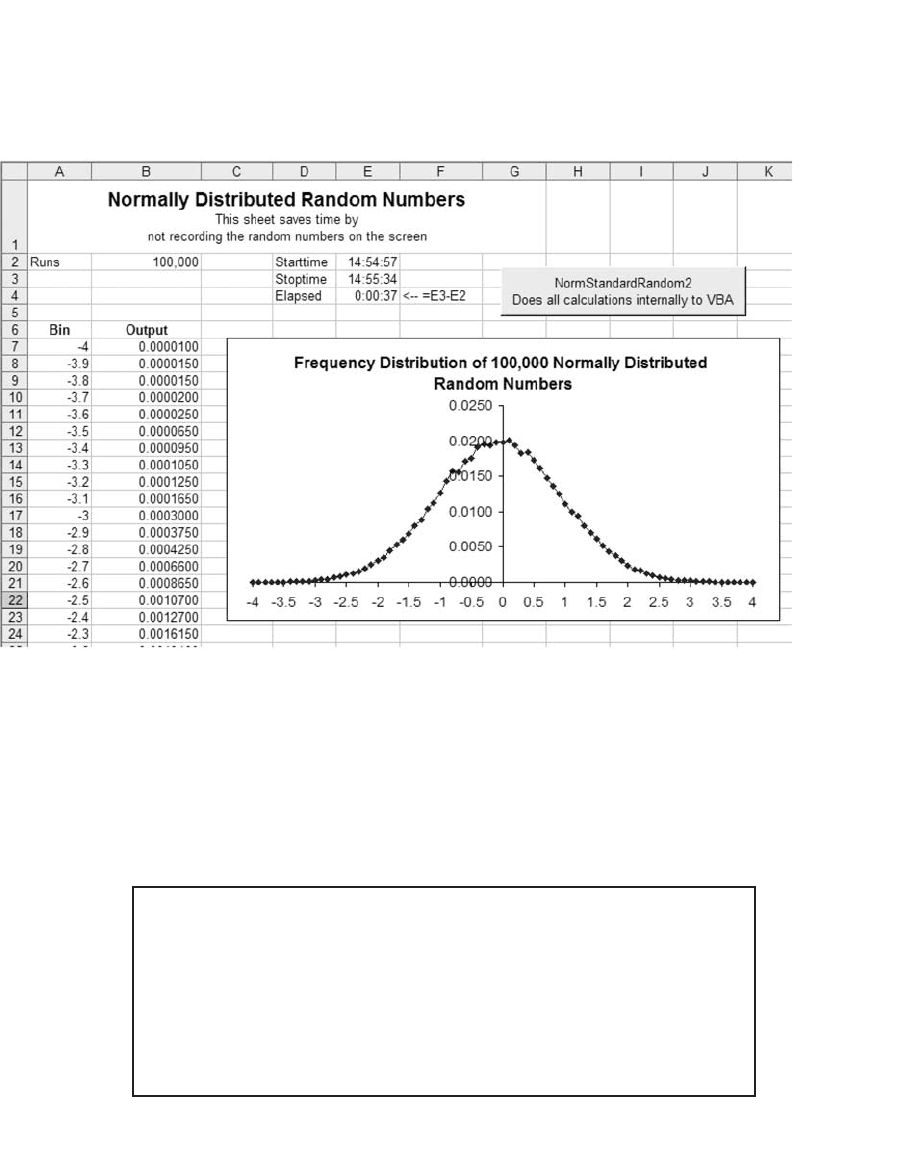
759 Generating Random Numbers

Here’s the output for 100,000 iterations. Note the time in cell E4.

There are a few things to note about this program:

•

Most of the results of the normal distribution are between −4 and +4.

When, in NormStandardRandom2, we classify the output into bins, we

want these bins to be (−∞, −3.9], (−2.9, −2.8], . . . , (−3.9, ∞). We ﬁ rst deﬁ ne

an array distribution(-40 To 40); this array has 81 indices. To

classify a particular random number (say X) into the bins of this array,

we use the following function:

If X < -4 Then

distribution(-40) = distribution(-40) + 1

ElseIf X > 4 Then

distribution(40) = distribution(40) + 1

Else: distribution(Int(X / 0.1)) = _

distribution(Int(X / 0.1)) + 1

End If

760 Chapter 29

•

NormStandardRandom2 produces not a histogram (which is a count

of how many times a number falls into a particular bin), but a frequency

distribution. We produce this by dividing by twice the number of runs

(remember that each successful run produces two random numbers), 2N,

before we output the data to the spreadsheet:

For Index = -40 To 40

Range(“output”).Cells(Index + 41, 1) = _

distribution(Index) / (2 * N)

Next Index

•

Finally, note that the command Application.ScreenUpdating =

False makes a big difference! This command prevents both the updat-

ing of the output in the cells and the Excel chart. Try running the program

with and without this command to see the effect.

29.4.4 Method 4: The Box-Muller Method

The Box-Muller method for creating randomly distributed normal devi-

ates is the fastest method of the four.

The eight lines that follow Start

in the VBA program deﬁ ne a routine, which in each successful iteration

creates two numbers that are drawn from a standard normal distribution.

The routine creates two random numbers, rand

and rand

, between −1

and +1. If the sum of the squares of these numbers is within the unit

circle, then the two normal deviates are deﬁ ned by

{, }

ln( )

12 1

=∗

−

∗

−

⎧

⎨

⎩

⎫

⎬

⎭

rand rand

where S

= rand

+ rand

Here’s the VBA program:

7. See Box-Muller (1958) or Knuth (1981).

Sub NormStandardRandom3()

‘Box-Muller for producing standard normal deviates

Dim distribution(-40 To 40) As Long

Range(“E2”) = Time

N = Range(“B2”).Value

Application.ScreenUpdating = False

For Index = 1 To N

start:

Static rand1, rand2, S1, S2, X1, X2

rand1 = 2 * Rnd - 1

rand2 = 2 * Rnd - 1

S1 = rand1 ^ 2 + rand2 ^ 2

If S1 > 1 Then GoTo start

S2 = Sqr(-2 * Log(S1) / S1)

X1 = rand1 * S2

X2 = rand2 * S2

If X1 < -4 Then

distribution(-40) = distribution(-40) + 1

ElseIf X1 > 4 Then

distribution(40) = distribution(40) + 1

Else: distribution(Int(X1 / 0.1)) = _

distribution(Int(X1 / 0.1)) + 1

End If

If X2 < -4 Then

distribution(-40) = distribution(-40) + 1

ElseIf X2 > 4 Then

distribution(40) = distribution(40) + 1

Else: distribution(Int(X2 / 0.1)) = _

distribution(Int(X2 / 0.1)) + 1

End If

Next Index

For Index = -40 To 40

Range(“B7”).Cells(Index + 41, 1) = _

distribution(Index) / (2 * N)

Next Index

Range(“E3”) = Time

End Sub

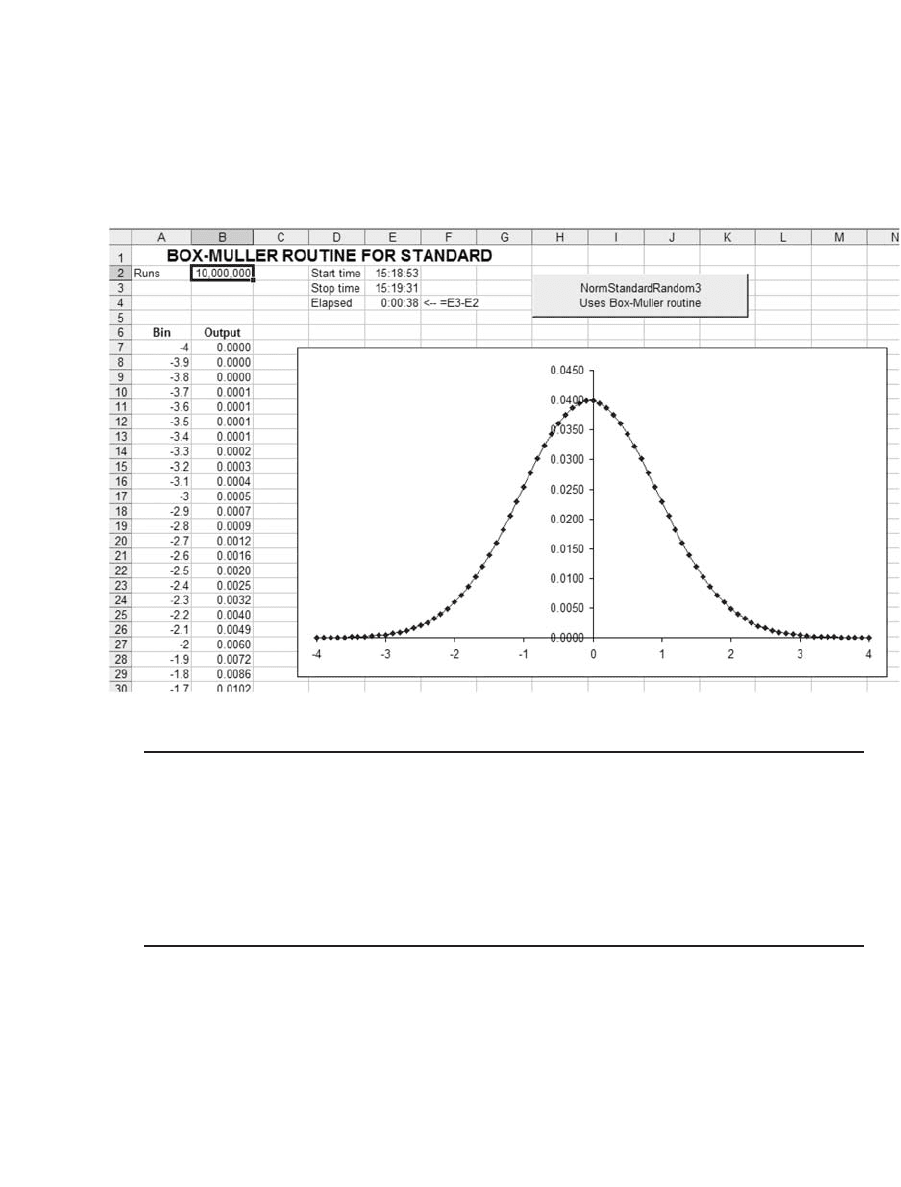
762 Chapter 29

This routine is very fast. In the following spreadsheet we produce 10

million normal variates in 38 seconds:

29.5 Summary

Random numbers are widely used in ﬁ nancial engineering, especially in

option pricing. This chapter has introduced you to the Excel and VBA

random-number generators and has shown a number of techniques for

producing normally distributed random numbers.

Exercises

1. Use the program RandomList from section 29.2.1 to produce a list of 200 random

numbers. Use the Excel function Frequency to produce a histogram of the results.

2. Here is a random-number generator you can make yourself:

a. Start with some number, Seed.

b. Let X

= Seed + π. Let X

= e

5+ln(X

)

763 Generating Random Numbers

c. The ﬁ rst random number is Random = X

− Integer(X

), where Integer(X

) is the

integer part of X

d. Repeat the process, letting Seed = Random.

Implement this random-number generator in a VBA program similar to

RandomList, and produce a list of 50 random numbers.

3. Deﬁ ne AmodB as the remainder when A is divided by B. For example, 36mod25 =

11. Excel has this function; it is written Mod(A,B). Now here is another random-

number generator:

a. Let X

= 1.

b. Let X

n+1

= (7 * X

)mod10

c. Let U

n+1

= X

n+1

/10

The list of numbers U

, U

, . . . contains the pseudo-random numbers generated by

this random-number generator. (This is one of the many random-number generators

given in Abramowitz and Stegun, 1972).

Use VBA to produce this random number generator, and use it in a program

similar to UniformRandom.

4. Many states have daily lotteries, which are played as follows: Sometime during the

day, you buy a lottery ticket, on which the seller inscribes a number you choose,

between 000 and 999. That night there is a drawing on television in which a three-

digit number is drawn. If the number on your ticket matches the number drawn,

you win and collect $500 (for a $1 wager). If you lose, you get nothing.

a. Write an Excel function that produces a random number between 000 and 999.

(Hint: Use Rand( ) and Int( ).)

b. Write a VBA program that reproduces 250 random draws of the daily lottery

(about one year’s worth, if there are no drawings on weekends). Assuming that

each ticket costs $1, and assuming that you choose the same number each day,

how much would you have won during the year?

5. Program normalSimulation but put the output into more bins (can you make the

number of bins and their size controllable from the spreadsheet?). Does this get rid

of the “fat tails” in the distribution graph?

6. It is well-known that if Z is a standard normal random variable (i.e., with mean

μ = 0 and standard deviation σ = 1) then X = aZ + b is normally distributed with

μ = b and σ = a. Modify normalSimulation to produce normal, nonstandard, distribu-

tions, with the mean and the standard deviation inputted from the spreadsheet.

7. a. Use NormSInv to produce a list of 1,000 random numbers and use Frequency to

see whether they are indeed normally distributed with mean μ = 0 and standard

deviation σ = 1.

b. Following exercise 6, modify the numbers so that they are distributed with μ = b

and σ = a.

Data Tables

30.1 Overview

Data table commands are powerful commands that make it possible to

do complex sensitivity analyses. Excel offers the opportunity to build a

table in which only one variable is changed, or one in which two variables

are changed. Excel data tables are array functions and thus change

dynamically when related spreadsheet cells are changed. In this chapter

you will learn how to build both one-dimensional and two-dimensional

Excel data tables.

30.2 An Example

Consider a project that has an initial cost of $1,150 and seven subsequent

cash ﬂ ows. The cash ﬂ ows in years 1–7 grow at rate g, so that the cash

ﬂ ow in year t is CF

= CF

t−1

(1 + g). Given a discount rate r, the net

present value (NPV) of the project is

NPV

CF g

=− +

++1

,150

()

...

()

The internal rate of return (IRR), i, is the rate at which the NPV equals

zero:

++1,150

CF g

()

...

(

)

()

These calculations are easily done in Excel. In the following example the

initial cash ﬂ ow is 234, the growth rate g = 10 percent, and the discount

rate r = 15 percent:

ABCDEFGHI

234

Growth rate 10%

Discount rate 15%

Year 01234567

Cash flow -1,150.00 234.00 257.40 283.14 311.45 342.60 376.86 414.55

NPV 101.46 <

=+B6+NPV(B3,C6:I6)

IRR 17.60% <

=IRR(B6:I6,0)

766 Chapter 30

Note the cell addresses for the growth rate, the discount rate, the NPV,

and the IRR. They will be needed in this chapter.

30.3 Setting Up a Data Table

Suppose we want to know how the NPV and IRR are affected by a

change in the growth rate. The command Data Table allows us to ﬁ nd

this information simply. The ﬁ rst step is to set up the table’s structure. In

the next example, we put the formulas for the NPV and IRR on the top

row, and we put the variable we wish to vary (in this case the growth

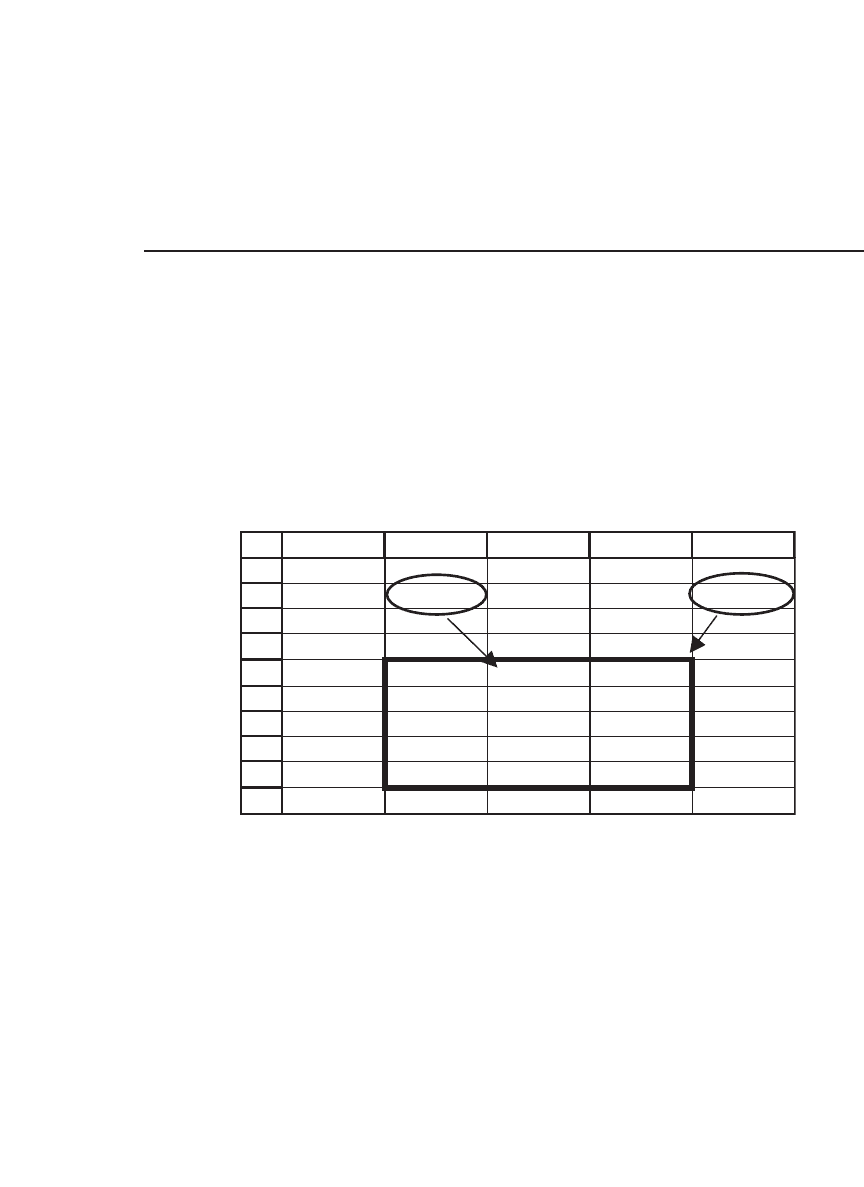
rate) in the ﬁ rst column. At this point the table looks like this:

FGH I J

=B8 =B9

NPV IRR

101.46 17.6%

Growth 5%

rate 10%

15%

The actual table (as opposed to the labels for the columns and the rows)

is outlined in the dark border. The numbers directly under the labels

“NPV” and “IRR” refer to the corresponding formulas in the previous

picture. Thus, if cell B8 contains the calculation for the NPV, then the

cell under the letters “NPV” contains the formula “=B8.” Similarly, if cell

B9 contains the original calculation for the IRR, then the cell under

“IRR” in the table contains the formula “=B9.”

767 Data Tables

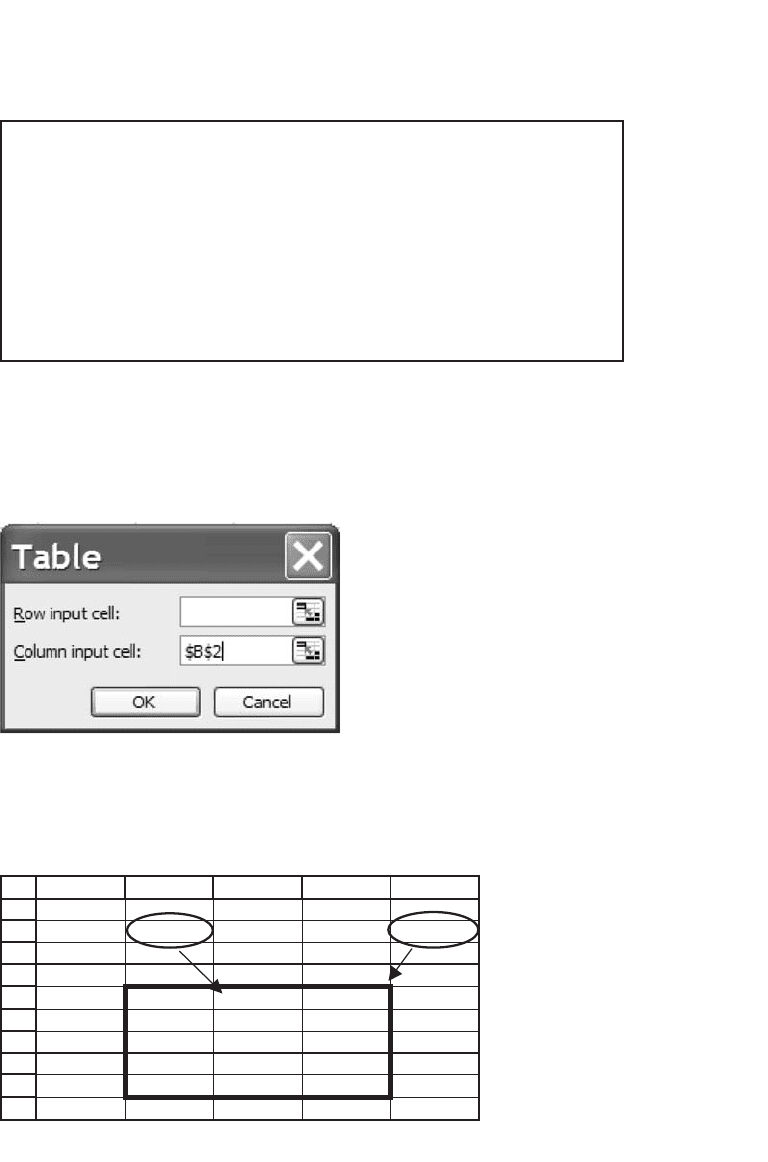
Now do the following:

•

Highlight the table area (outlined in the dark border).

•

Activate the command Data|Table. You will get a dialogue box that

asks you to indicate a Row Input Cell and/or a Column Input Cell.

We like to think of a data table spreadsheet as having two parts:

1. A basic example.

2. A table that does a sensitivity analysis on the basic example. In

our example, the ﬁ rst row of the table contains references to

calculations done in our basic example. While there are other

ways to do data tables, this structure is both typical and easy

to understand.

In this case, the variable we wish to change is in the left-hand column of

our table, so we leave the Row Input Cell blank and indicate cell B2 (this

cell contains the growth rate in our basic example) in the Column Input

Cell box. Here’s the result:

FGH I J

=B8 =B9

NPV IRR

101.46 17.6%

0 -176.46 9.71%

Growth 5% -47.82 13.67%

rate 10% 101.46 17.60%

15% 274.35 21.50%