Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

768 Chapter 30

30.4 Building a Two-Dimensional Data Table

We can also use the Data Table command to vary one formula while

changing two parameters. Suppose, for example, that we want to calculate

the net present value (NPV) of the cash ﬂ ows for different growth rates

and different discount rates. We create a new table that looks like this:

EFGH I JK

=B8

Discount rate

101.46 7% 10% 12%

Growth 0

rate 5%

10%

15%

The upper left-hand corner of the table contains the formula “=B8” as a

reference to the basic example.

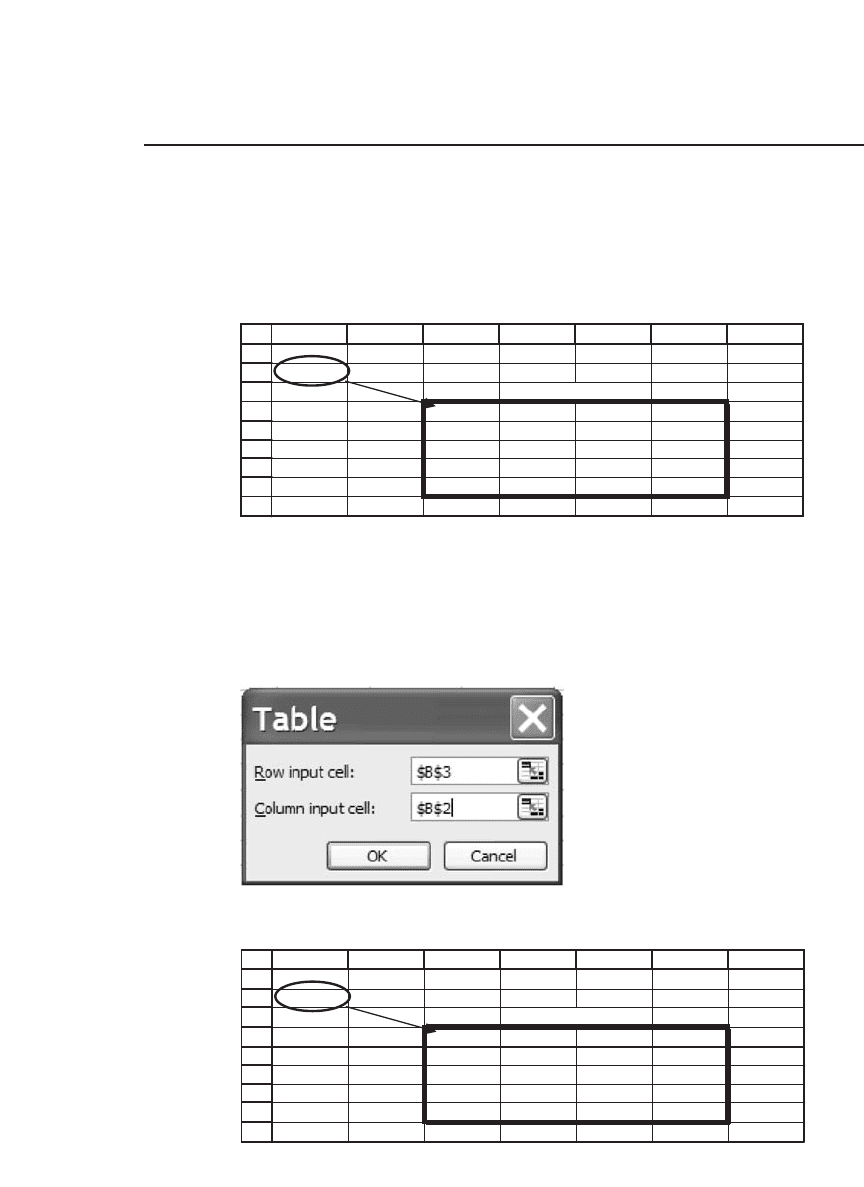
We now use the Data Table command again. This time we ﬁ ll in both

the Row Input Cell (indicating cell B3, the site of the discount rate in

our basic example) and the Column Input Cell (indicating B2).

EFGH I JK

=B8

Discount rate

101.46 7% 10% 12%

Growth 0 111.09 -10.79 -82.08

rate 5% 297.62 150.74 65.13

10% 515.79 339.09 236.44

15% 770.34 558.25 435.41

Here’s the result:

769 Data Tables

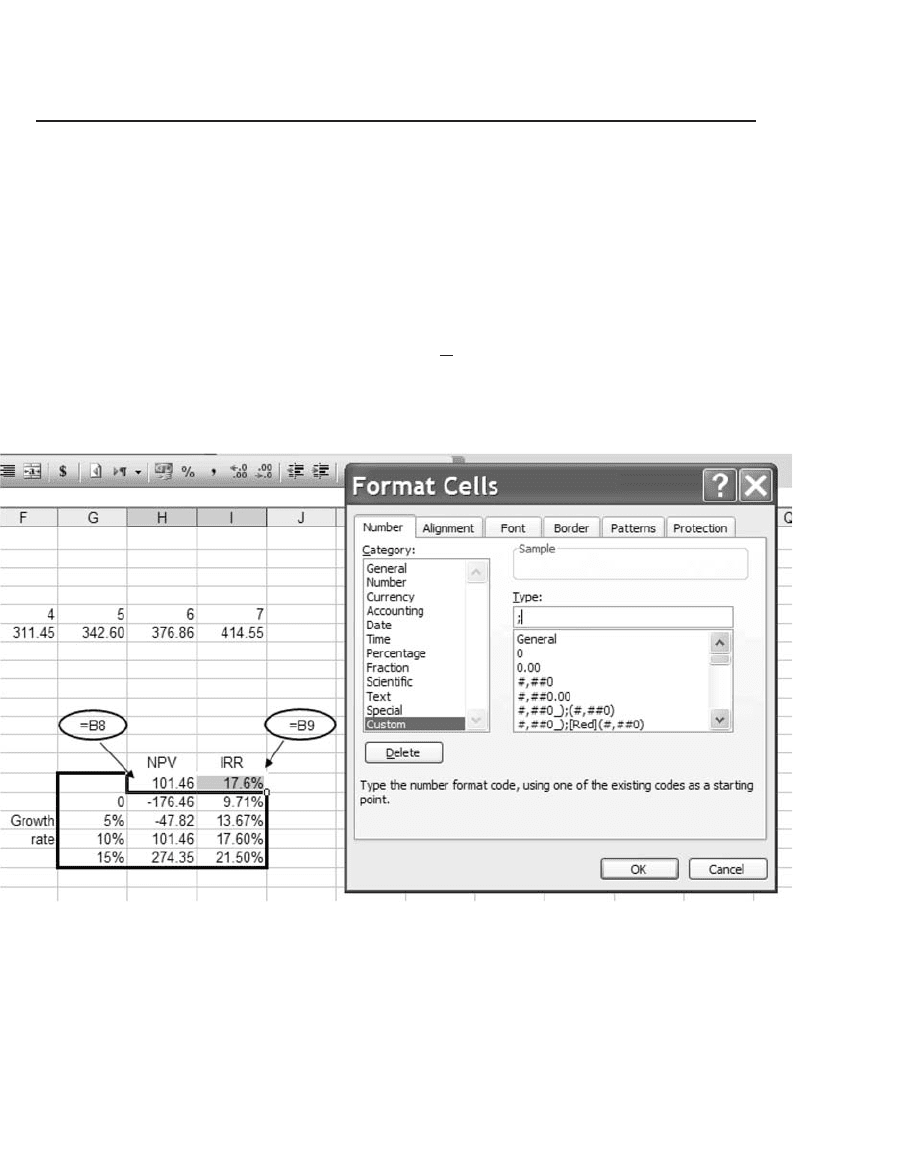
30.5 An Aesthetic Note: Hiding the Formula Cells

Data tables tend to look a bit strange, because the formula being calcu-

lated shows up in the data table (in our examples: in the top row of the

ﬁ rst data table and in the left-hand top corner of the second data table).

You can make your tables look nicer by hiding the formula cells. To do

this, mark the offending cells and use the Format Cells command (or

press the right mouse button and go to the Number|Custom). In the

dialogue box go to the box marked Type and insert a semicolon into the

box. Here’s the way this screen looks for the previous example:

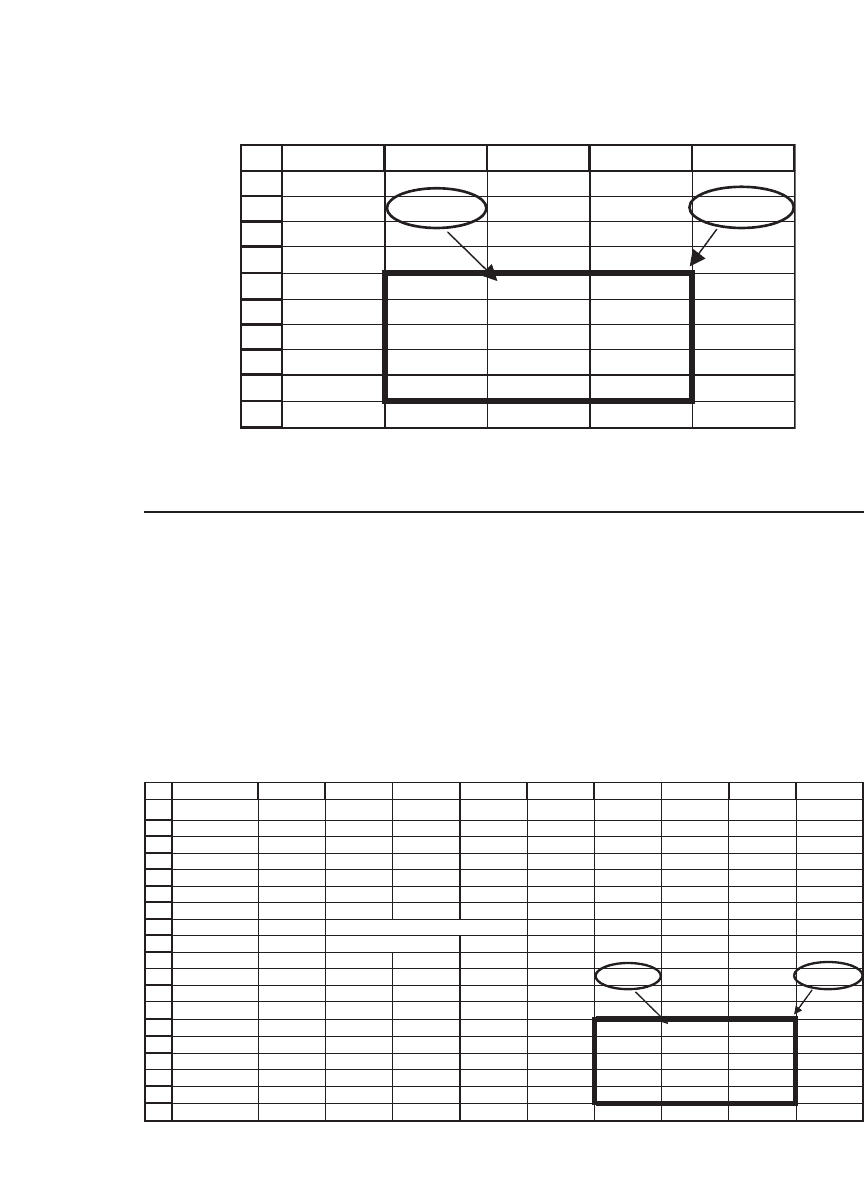
The cell contents will now be hidden. The result looks like the

following:

770 Chapter 30

30.6 Excel Data Tables Are Arrays

When we say that Excel data tables are arrays, we mean that they are

dynamically linked to the initial example. When we change a parameter

in the original example, the corresponding column or row of the data

table changes. For example, if we change the initial cash ﬂ ow from 234

to 300, here’s what will happen in the preceding data table:

FGH I J

=B8 =B9

NPV IRR

0 -176.46 9.71%

Growth 5% -47.82 13.67%

rate 10% 101.46 17.60%

15% 274.35 21.50%

ABCDEFGHIJ

300

Growth rate 10%

Discount rate 15%

Year 01234567

Cash flow -1150.00 300.00 330.00 363.00 399.30 439.23 483.15 531.47

NPV 454.43 <

=+B6+NPV(B3,C6:I6)

IRR 26.01% <

=IRR(B6:I6,0)

=B8 =B9

NPV IRR

0 98.13 17.80%

Growth 5% 263.06 21.92%

rate 10% 454.43 26.01%

15% 676.09 30.07%

771 Data Tables

Exercises

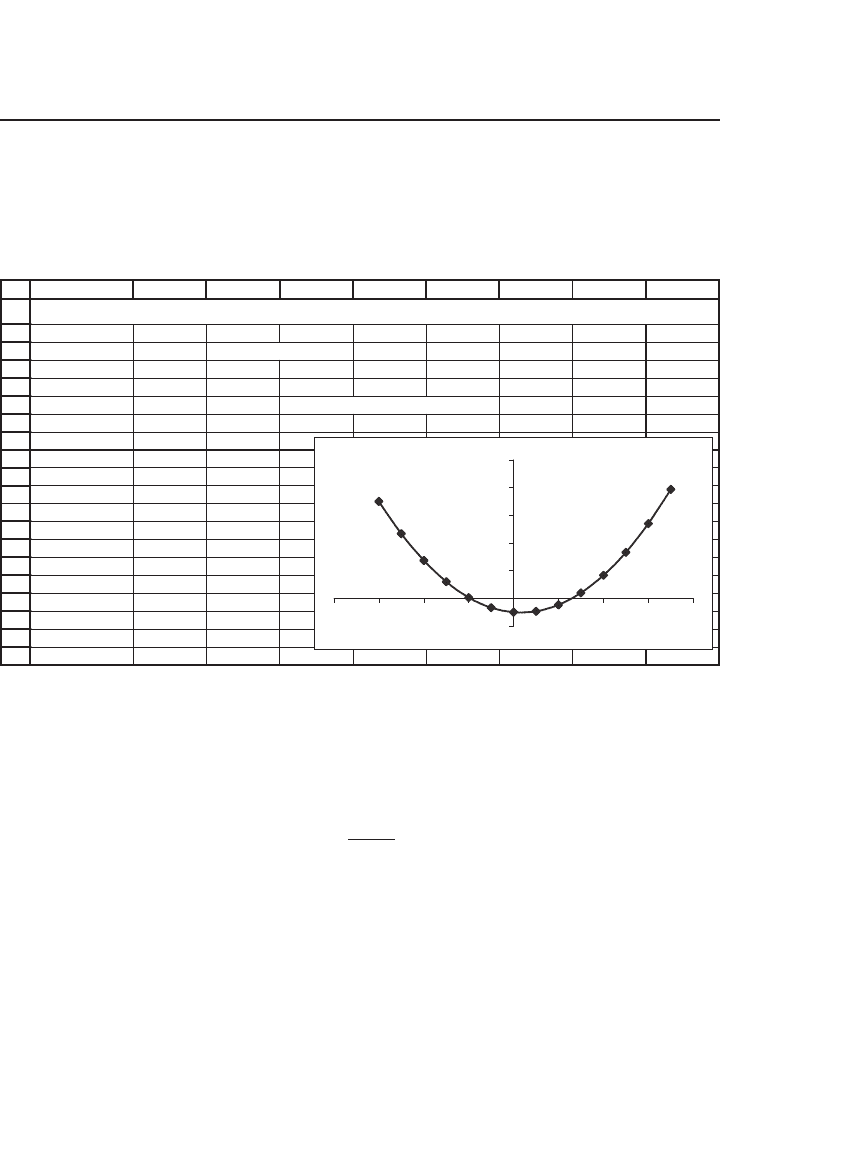
1. a. Use Data|Table to graph the function f(x) = 3x

− 2x − 15, as illustrated in this

spreadsheet:

ABCDEFGHI

f(x) 6 <

=3*B2^2-2*B2-15

x6<

=B3, data table header

-6 105

-5 70

-4 41

-3 18

-2 1

-1 -10

0-15

1-14

2-7

425

550

681

7118

USING DATA TABLE TO GRAPH A FUNCTION

-30

120

150

-8 -6 -4 -2 0 2 4 6 8

b. Use Solver or Goal|Seek to ﬁ nd two values of x, for which f(x) = 0.

2. The Excel function PV(rate, number_periods, payment) calculates the present value

of a constant payment. Thus in the following spreadsheet example,

PV(15 percent, 15, −= =

∑

115

58 47

)

(. )

(Note that we have put the payment as a negative number, since otherwise Excel

returns a negative value! This little irritation is discussed in Chapters 1 and 33.)

Use Data Table to graph the present value as a function of the discount rate, as

follows:

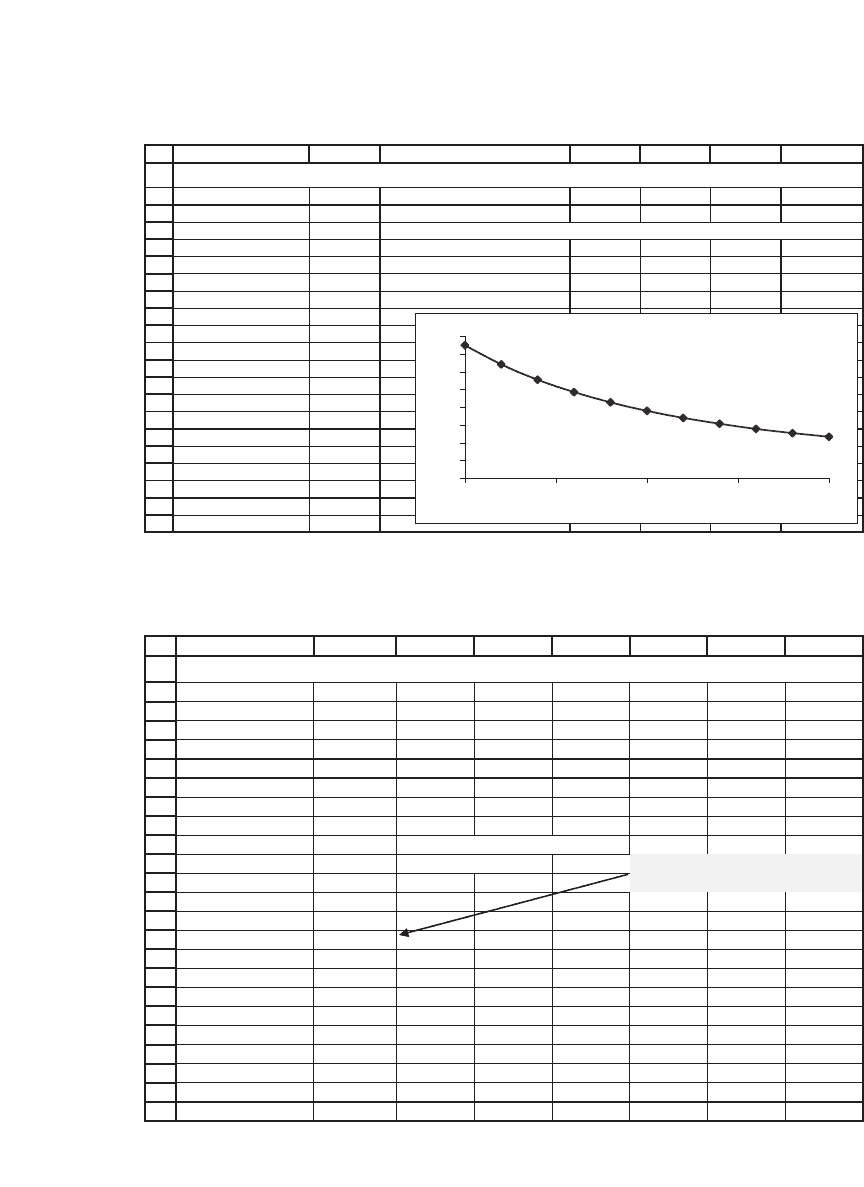
772 Chapter 30

AB C DEFG

15%Rate

Number of periods 15

Payment -10 To get a positive PV, we let the payment be negative (see Chapters 1 & 34)

Present value $58.47 <

=PV(B2,B3,B4)

Rate

$58.47 <

=B5, data table header

0% 150.00

2% 128.49

4% 111.18

6% 97.12

8% 85.59

10% 76.06

12% 68.11

14% 61.42

16% 55.75

18% 50.92

20% 46.75

DATA TABLE AND PV

100

120

140

160

0% 5% 10% 15% 20%

3. The following spreadsheet fragment shows a net present value and internal rate of

return calculation for a project:

ABCDEFGH

Growth rate 10%

Discount rate 15%

005tsoC

Year 1 cash flow 100

Year 0 1 2 3 4 5

Cash flow -500.00 100.00 110.00 121.00 133.10 146.41

NPV (101.42) <

=NPV(B3,C8:G8)+B8

IRR 6.60% <

=IRR(B8:G8)

Growth

($101.42) 0% 3% 6% 9% 12%

0% 0.00 30.91 63.71 98.47 135.28

Discount rate

3% -42.03 -14.56 14.55 45.38 78.01

6% -78.76 -54.26 -28.30 -0.84 28.21

9% -111.03 -89.08 -65.85 -41.28 -15.33

12% -139.52 -119.78 -98.91 -76.86 -53.57

15% -164.78 -146.97 -128.15 -108.28 -87.32

18% -187.28 -171.15 -154.13 -136.16 -117.23

21% -207.40 -192.75 -177.30 -161.01 -143.84

24% -225.46 -212.11 -198.04 -183.22 -167.62

Cell B15 contains the data table

function =B10

NPV, DISCOUNT AND GROWTH RATES

773 Data Tables

Use Data Table to do a sensitivity analysis on the NPV of the project for discount

rates 0, 3, 6, . . . , 21 percent and growth rates 0, 3, . . . , 12 percent.

4. Using Data Table, graph the function sin(x

y) for x = 0, 0.2, 0.4, . . . , 1.8, 2 and y =

0, 0.2, 0.4, . . . , 1.8, 2. Use the “Surface” graph option to make a three-dimensional

graph of the function.

Matrices

31.1 Overview

The portfolio optimization chapters of Financial Modeling (Chapters

8–15) make extensive use of matrices to ﬁ nd efﬁ cient portfolios. This

chapter contains enough information about matrices to make it possible

for you to follow the discussion (and do the calculations!) required for

portfolio mathematics.

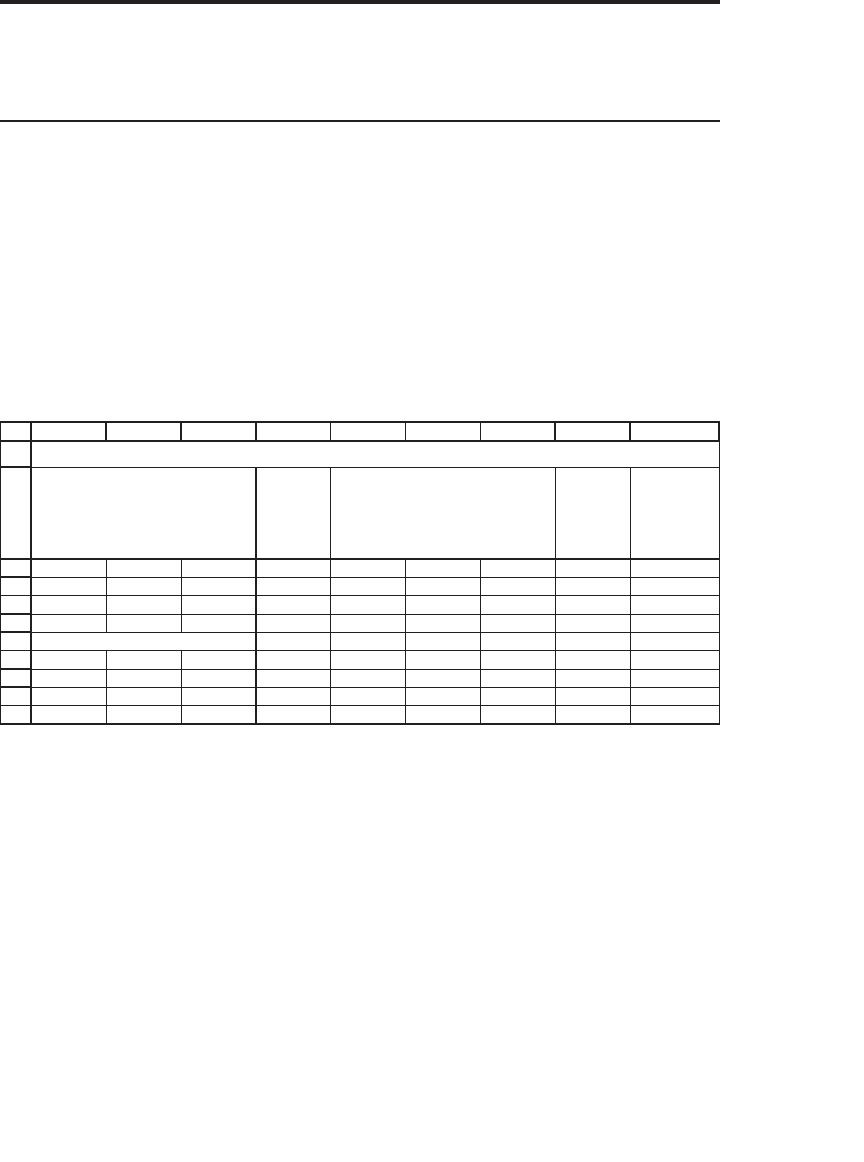
A matrix is a rectangular array of numbers. All of the following are

matrices:

ABCDEFGH I

Matrix C

(column

vector)

234 13-8-3

-8 10 -1 -8

-3 -1 11 -3

13 -8 -3

-8 10 -1

-3 -1 11

013 3

Matrix D (a 4 x 3 matrix)

Matrix A (a row vector) Matrix B (square 3 x 3 matrix)

MATRICES IN EXCEL

A matrix with only one row is also called a row vector; a matrix with

only one column is also called a column vector. A matrix with an equal

number of rows and columns is called a square matrix.

A single letter is often used to denote a matrix or a vector. In this case

we often write, for example, B = [b

], where b

stands for the entry in

row i and column j of the matrix. For a vector we might write A = [a

] or

C = [c

]. Thus, for the examples given,

ab c d

322 1 41

4101310=== =

The matrix B is symmetric, meaning that b

= b

. (The variance-

covariance matrices used in the portfolio discussion of Chapters

8–13 are symmetric.)

776 Chapter 31

31.2 Matrix Operations

In this section we brieﬂ y review the basic operations on a matrix: multi-

plying a matrix by a scalar, adding matrices, transposition of matrices,

and matrix multiplication.

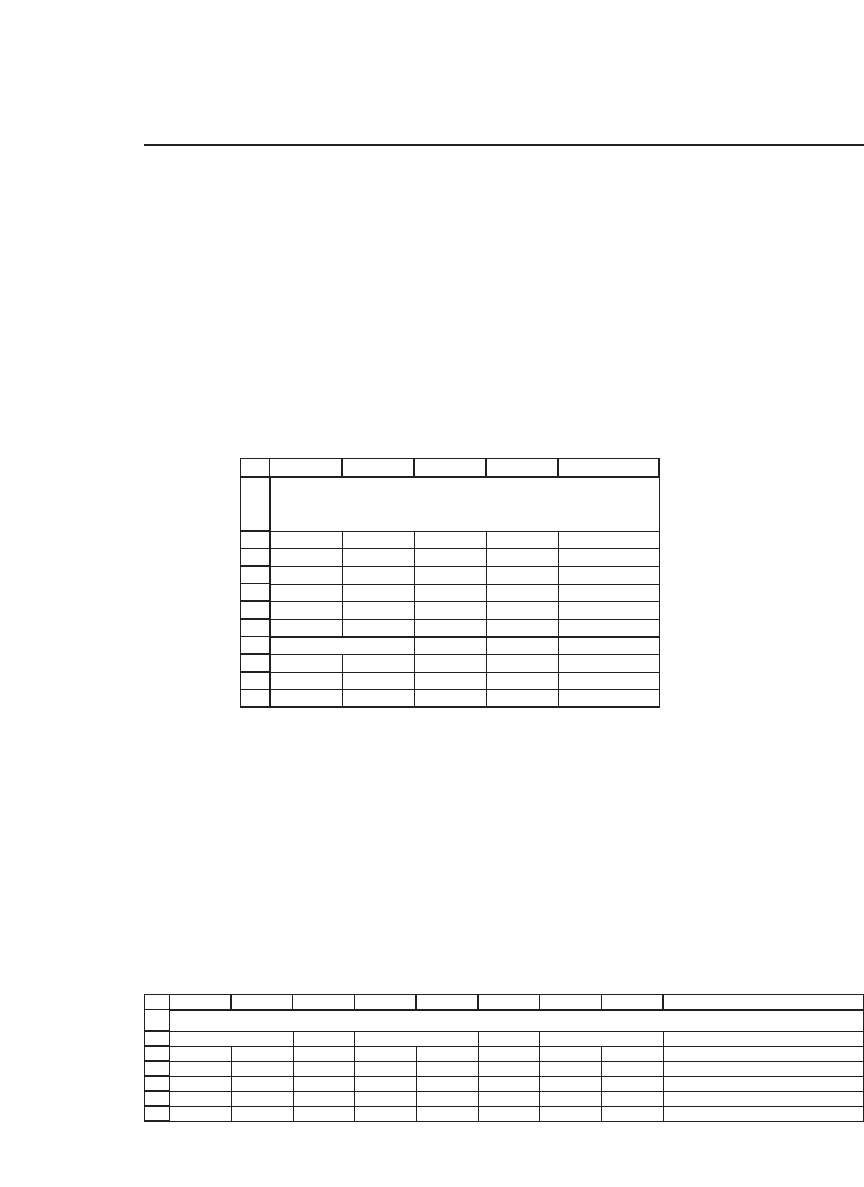
31.2.1 Multiplication by a Scalar

Multiplying a matrix by a scalar multiplies every entry in the matrix by

the scalar, as in this example:

ABCD E

Scalar 6

Matrix B 13 -8 -3

-8 10 -1

-3 -1 11

Scalar * Matrix B

78 -48 -18 <

=D4*$B$2

-48 60 -6

-18 -6 66

MULTIPLYING A MATRIX BY A SCALAR

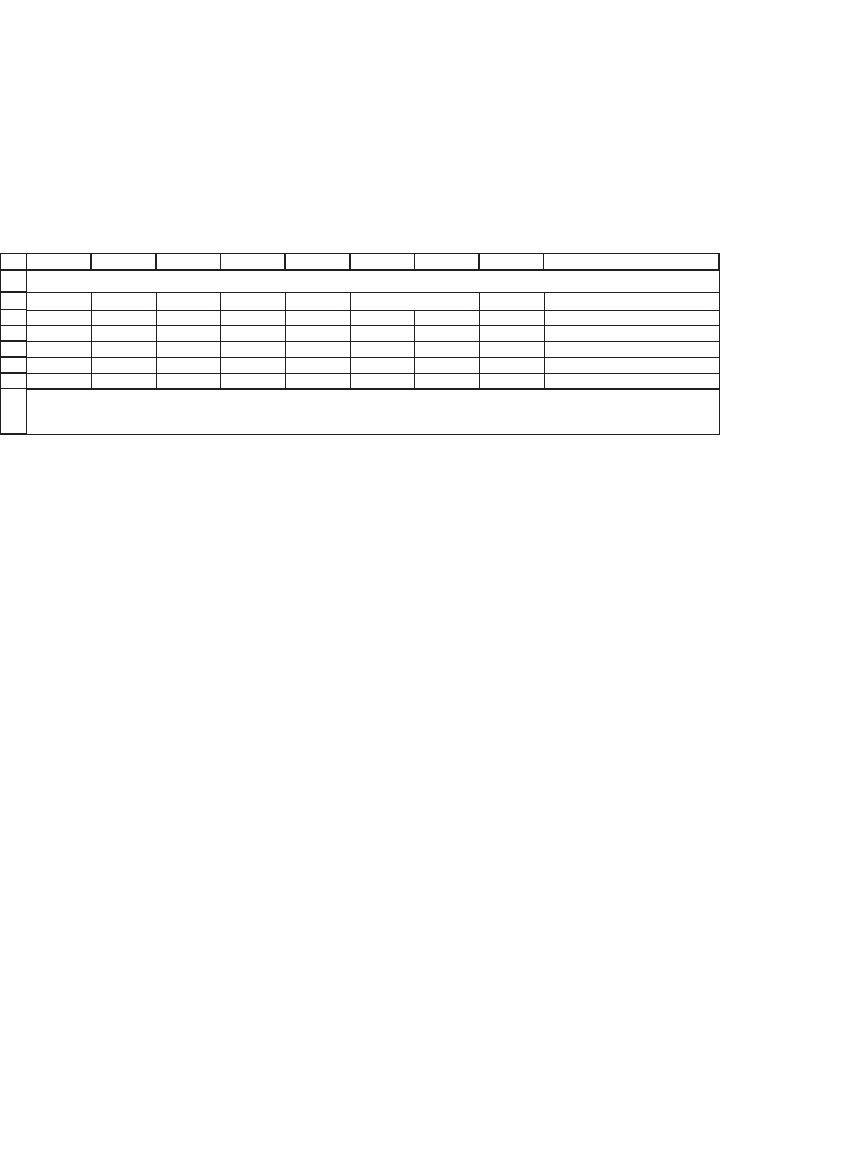
31.2.2 Matrix Addition

Matrices may be added together provided they have the same number

of rows and columns. Adding two vectors or matrices is accomplished

by adding their corresponding entries. Thus if A = [a

] and B = [b

A + B = [a

+ b

ABCDEFGH I

Sum of A + B

1 3 0.1 0 1.1 3 <

=B3+E3

30 230 260

6 -9 8 -33.4 14 -42.4

5 11 -15 0 -10 11

7 12 2.33 1.2 9.33 13.2

Matrix A Matrix B

ADDITION OF MATRICES

777 Matrices

31.2.3 Matrix Transposition

Transposition is an operation by which the rows of a matrix are turned

into columns and vice versa. Thus for the matrix E:

ABCDEFGH I

Matrix E

Transpose of E: E

1234 1016<

{=TRANSPOSE(A3:D5)}

0377-9 237

16 7 7 2 3 77 7

4-9 2

Cells F3:H6 are generated with the array function Transpose(A3:D5). This function is inserted by marking off the target

area, typing the formula, and then finishing by pressing [Ctrl]+[Shift]+[Enter] . See Chapter 34 for more details.

TRANSPOSITION OF MATRICES

This illustration uses the array function Transpose. More details on the

use of array functions are given in Chapter 34.

31.2.4 Multiplication of Matrices

You can multiply matrix A by matrix B to get product AB. However,

you can only do so if the number of columns in A equals the number of

rows in B. The resulting product AB is a matrix with the number of rows

as A and the number of columns of B.

Confused? A couple of examples will help. Suppose that X is a row

vector and that Y is a column vector, both with n coordinates:

XY=

[]

⎡

⎣

⎢

⎤

⎦

⎥

... ,



Then the product of X and Y is deﬁ ned by

XY =

⎡

⎣

⎢

⎤

⎦

⎥

∑

[ ... ]xx

ii1



Now suppose that A and B are two matrices, and that A has n columns

and p rows and B has n rows and m columns: