Simon Benninga. Financial Modelling 3-rd edition
Подождите немного. Документ загружается.

738 Chapter 28
If we assume that the corporate tax rate is T
C
= 40 percent, then the
tax-adjusted CAPM gives the following betas:
E(r
M
)
8%
r
f
3.90%
Recovery
percentage,
l
Annual
transition
matrix
Semiannual
transition
matrix
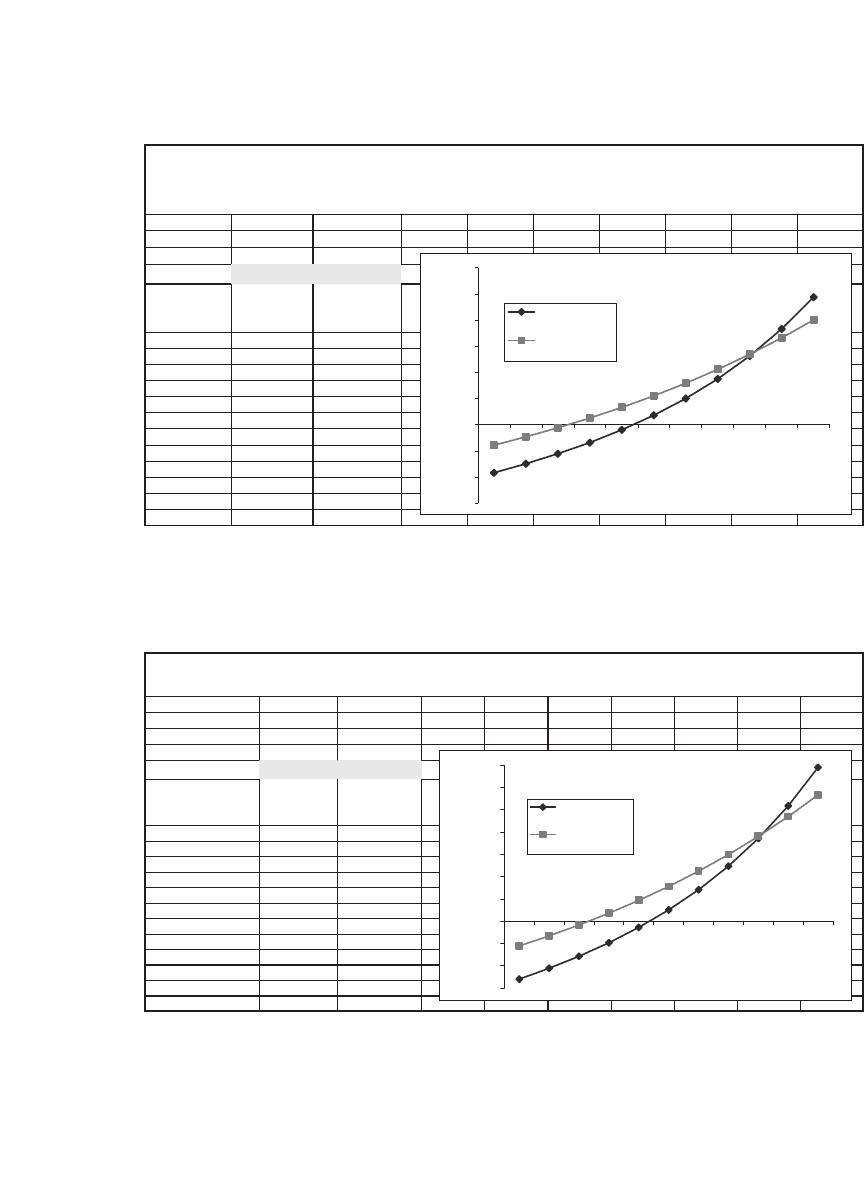
0% -1.84 -0.79
10% -1.49 -0.47
20% -1.11 -0.12
30% -0.68 0.25
40% -0.20 0.66
55% 0.36 1.10
60% 1.00 1.59
65% 1.75 2.11
80% 2.63 2.69
90% 3.66 3.32
100% 4.88 4.01
COMPARING AMR BOND BETAS
SEMIANNUAL VS. ANNUAL TRANSITION MATRICES
Using actual dates and XIRR
BOND BETA
AMR BOND BETAS
-3.00
-2.00
-1.00
0.00
1.00
2.00
3.00
4.00
5.00
6.00
0
Recovery percentage
l (%)
Bond beta
Annual
transition matrix
Semiannual
transition matrix
100908065605540302010
E(r
M
)
8%
r
f
3.90%
Corp. tax rate, T
C
40.00%
Recovery
percentage, l
Annual
transition
matrix
Semiannual
transition
matrix
0% -1.30 -0.56
10% -1.06 -0.33
20% -0.79 -0.08
30% -0.48 0.18
40% -0.14 0.47
55% 0.25 0.78
60% 0.71 1.12
65% 1.24 1.50
80% 1.86 1.90
90% 2.59 2.35
100% 3.45 2.84
COMPARING AMR BOND BETAS
Using the tax-adjusted CAPM (section 2.6)
BOND BETA
AMR BOND BETAS
Tax-adjusted CAPM
-1.50
-1.00
-0.50
0.00
0.50
1.00
1.50
2.00
2.50
3.00
3.50
0
Recovery percentage l (%)
Annual
transition matrix
Semiannual
transition matrix
Bond beta
10080604020
If these bond betas seem large, note that the AMR bond has a maturity
comparable to these long-term Treasury bonds and has in addition con-
siderable default risk. Another fact that helps place the AMR bond beta
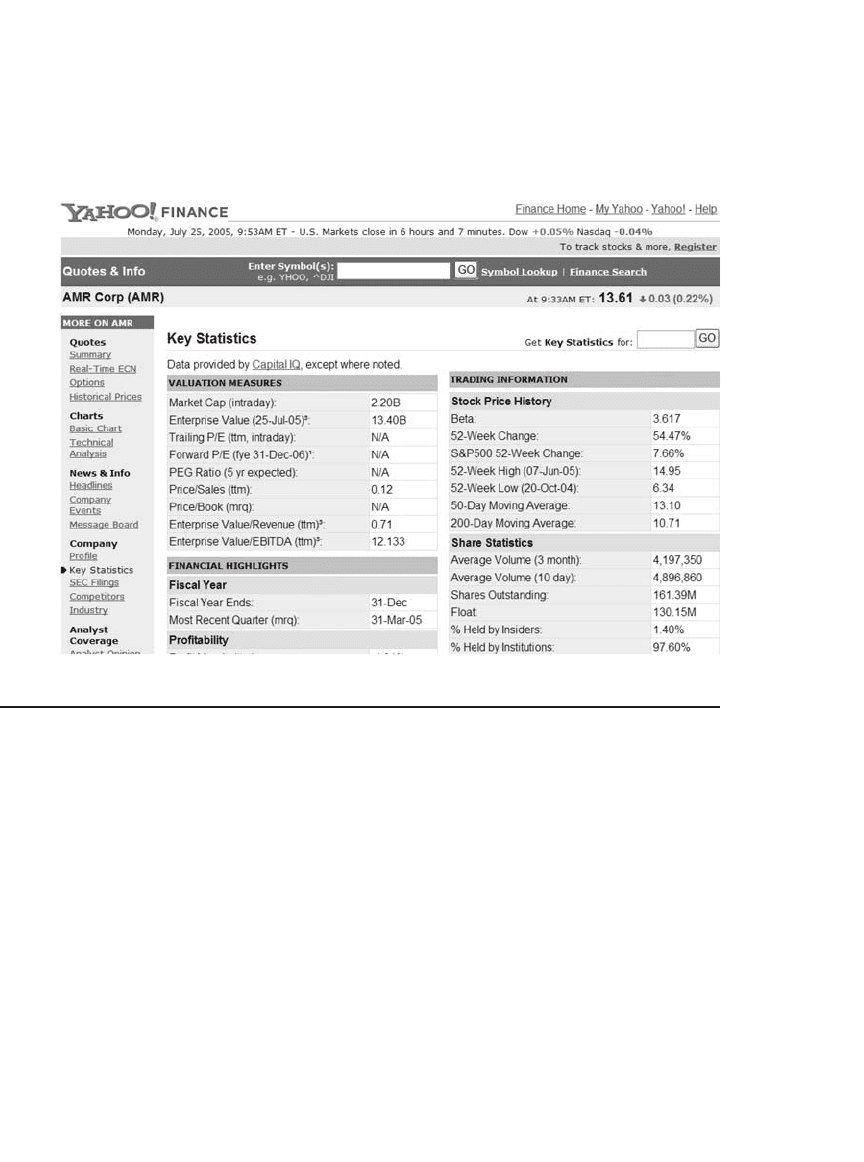
739 Calculating Default-Adjusted Expected Bond Returns
into context is AMR’s stock beta. According to Yahoo this beta is
3.617:
28.9 Summary
In this chapter we have shown how to compute the expected return on
a risky bond using a simple technique involving rating transitions. Com-
puting a bond’s expected returns puts the bond analysis on the same
footing as the analysis of stocks. Expected returns—common in the anal-
ysis of stocks—are rarely computed for bonds, where the common analy-
sis is in terms of yields to maturity. But the yield to maturity of a bond,
essentially the bond’s IRR based on its promised future payments,
includes an ill-defi ned premium for the bond’s default.
Having computed a bond’s expected return, we can then compute its
beta using the security market line (SML). Compared to the vast efforts
to compute and calibrate stock betas, relatively little research energy has
been expended on bond betas. The technique illustrated in this chapter,
based on the transition matrix of the bond ratings, is relatively new. This

740 Chapter 28
technique still has to be refi ned and thoroughly tested by academic
research. Several refi nements to the rating-based technique for comput-
ing expected bond returns still need to be explored. These include
•
Better transition matrices. Transition matrices need to be refi ned, and
perhaps made industry specifi c. (The problem with industry-specifi c data
is that the number of observations drops dramatically. Nevertheless,
there are examples of such data [for example, an S&P study from 2004
on real-estate–backed loans; see the citation in the bibliography].)
•
Time-dependent transition matrices. Our technique assumes that
transition matrices are stationary—constant through time. Perhaps
better techniques can be developed that allow for matrices to change
with time. For example, we would expect that in diffi cult economic condi-
tions the ratings transition matrix would “shift to the right”—that the
probabilities of a given rating getting worse over any period would
increase.
•
More data on recovery ratios.
Exercises
1. A newly issued bond with one year to maturity has a price of 100, which equals its
face value. The coupon rate on the bond is 15 percent; the probability of default in
one year is 35 percent; and the bond’s payoff in default will be 65 percent of its face
value. Calculate the bond’s expected return.
2. Consider a case of fi ve possible rating states, A, B, C, D, and E. States A, B, and C
are initial bond ratings, D symbolizes fi rst-time default, and E indicates default in
the previous period. Assume that the transition matrix Π is given by
=
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
10000
0 06 0 90 0 03 0 01 0
0 02 0 05 0 88 0 05 0
00001
00001
....
....
⎤⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
∏
A 10-year bond issued today at par with an A rating is assumed to bear a coupon
rate of 7 percent.
a. If a bond is issued today at par with a B rating and with a recovery percentage
of 50 percent, what should its coupon rate be so that its expected return will also
be 7 percent?
b. If a bond is issued today at par with a C rating and with a recovery percentage
of 50 percent, what should its coupon rate be so that its expected return will be
7 percent?

741 Calculating Default-Adjusted Expected Bond Returns
3. Using the transition matrix from exercise 2: A C-rated bond is selling at par on 18
July 2007. The bond’s maturity is 17 July 2017, it has a coupon (paid annually on 17
July) of 11 percent, and it has a recovery percentage of λ = 67 percent. What is the
bond’s expected return?
4. An underwriter issues a new seven-year B bond with a coupon rate of 9 percent. If
the expected rate of return on the bond is 8 percent, what is the bond’s implied
recovery percentage λ? Assume the transition matrix given in section 28.5.
5. An underwriter issues a new seven-year C-rated bond at par. The anticipated recov-
ery rate in default of the bond is expected to be 55 percent. What should the coupon
rate on the bond be so that its expected return is 9 percent? Assume the transition
matrix from exercise 2.


V
Technical Considerations
Chapters 29–35 cover a variety of technical subjects that are used in
Financial Modeling. Chapter 29 discusses the generation of random
numbers. The book uses random number generation extensively in
Chapter 18 (simulating stock prices), Chapter 21 (simulating portfolio
insurance), and Chapters 22 and 23 (Monte Carlo methods). Chapter 30
considers data tables. This is a basic Excel tool that allows us to build
sophisticated sensitivity tables. It is used throughout Financial Modeling.
Chapter 31 deals with matrices, used in the book to do portfolio optimi-
zation (Chapters 8–13). Chapter 32 discusses the Gauss-Seidel iterative
method for solving simultaneous equations. This method, though never
explicitly used in Financial Modeling, underlies the pro forma models of
Chapters 3 and 4. Chapter 33 is a compendium of Excel functions used
in the book. Chapter 34 discusses the use of array functions, with a special
emphasis on homemade array functions. Chapter 35 discusses a grab-bag
of Excel tricks that are used in various places in this book: Fast copying;
graph titles that update automatically; creating multiline cells; putting
Greek symbols, subscripts, and superscripts into Excel text; naming cells;
hiding cells; some formatting tricks; and formula auditing. This chapter
also shows how to add our auditing tool Getformula to your
spreadsheets.


29
Generating Random Numbers
29.1 Overview
In several of the option chapters of this book we have used randomly
generated stock prices to simulate and price options (see in particular
Chapter 18 on the lognormal distribution, Chapter 20 on option Greeks,
Chapter 21 on portfolio insurance, and Chapters 22–23 on Monte Carlo
methods). In all these chapters, the stock price simulations are based on
the generation of random numbers. In this chapter we discuss techniques
for computing these numbers.
A random-number generator on a computer is a function that
produces a seemingly unrelated set of numbers. The question of what
is a random number is a philosophical one.
1
In this chapter we will
ignore philosophy and concentrate on some simple random-number
generators—primarily the Excel random-number generator Rand( ) and
the VBA random-number generator Rnd.
2
To imagine a set of uniformly distributed random numbers, think of
an urn fi lled with 1,000 little balls, numbered 000, 001, 002, . . . , 999.
Suppose we perform the following experiment: Having shaken the urn
to mix up the balls, we draw one ball out of the urn and record the ball’s
number. Next we put the ball back into the urn, shake the urn thoroughly
so that the balls are mixed up again, and then draw out a new ball. The
series of numbers produced by repeating this procedure many times
should be uniformly distributed between 000 and 999.
A random number generator on a computer is a function that imitates
this procedure. The random-number generators considered in this chapter
are sometimes termed pseudo-random-number generators, since they are
actually deterministic functions whose values are indistinguishable from
random numbers. All pseudo-random-number generators have cycles
(that is, they eventually start to repeat themselves). The trick is to fi nd a
random-number generator with a long cycle. The Excel Rand( ) function
has very long cycles and is a respectable random-number generator.
1. Knuth (1981, p. 142) gives the following quote: “A random sequence is a vague notion
embodying the idea of a sequence in which each term is unpredictable to the uniniti-
ated and whose digits pass a certain number of tests, traditional with statisticians and
depending somewhat on the uses to which the sequence is to be put” (attributed to
D. H. Lehmer, 1951).
2. In this book we usually write Excel functions in boldface without the parentheses. In
this chapter we generally write Rand( ) with the parentheses to emphasize (a) that the
parentheses are necessary and (b) that they are empty.
746 Chapter 29
If you’ve never used a random-number generator, open an Excel
spreadsheet and type =Rand( ) in any cell. You will see a 15-digit number
between 0.000000000000000 and 0.999999999999999. Every time you
recalculate the spreadsheet (for example, by hitting the F9 button), the
number changes. We leave the technical details of how Rand( ) works
for the exercises to this chapter, where we show you how to design your
own random-number generator. Suffi ce it to say, however, that the series
of numbers produced by the function should be (to use Lehmer’s termi-
nology from footnote 1) “unpredictable to the unitiated.”
In this chapter we shall deal with several kinds of random-number
generators: We fi rst examine the uniform random-number generators
that come with Excel and VBA. Subsequently we generate normally
distributed random numbers.
3
29.2 Rand( ) and Rnd: The Excel and VBA Random-Number Generators
Suppose you simply wanted to generate a list of random numbers. One
way to do so would be to copy the Excel function Rand( ) to a range of
cells:
1
2
3
4
5
6
7
8
9
10
11
12
ABCD E
0.6337 0.7903 0.9283 0.0302 <
--
=RAND()
0.5041 0.6606 0.1293 0.1976
0.9407 0.9486 0.8677 0.4154
0.9351 0.2060 0.9635 0.1074
0.8297 0.4525 0.6394 0.8085
0.5973 0.5655 0.8531 0.2139
0.6800 0.7932 0.9045 0.9724
0.7789 0.4750 0.7291 0.8122
0.0466 0.7387 0.2422 0.8827
Each cell contains the function Rand( ). Each time you
update the spreadsheet or press F9 the block of cells will
produce a new set of random numbers.
USING EXCEL'S RAND( ) FUNCTION
3. A common nomenclature speaks of “random deviates.” Only in fi nancial engineering
can one fi nd “normal deviates!”
747 Generating Random Numbers
In section 30.3 we will develop a crude test of how well Rand( )
works.
29.2.1 Using VBA’s Rnd Function
VBA contains its own function Rnd which is equivalent to the Excel
Rand function.
4
Here’s a small VBA program that illustrates a basic use
of the Rnd function:
Sub RandomList()
‘Produces a simple list of random numbers
For Index = 1 To 10
Range(“A4”).Cells(Index, 1) = Rnd
Next Index
End Sub
In the next spreadsheet, the VBA program has been assigned to a
button, so that each time we click on the button, it runs a VBA program
that produces 10 random numbers:
Sub RandomList()
‘Produces a simple list of random numbers
For Index = 1 To 10
Range(“A3”).Cells(Index, 1) = Rnd
Next Index
End Sub
On the spreadsheet fm3_chapter29.xls, which comes with this chapter,
you can push a button to operate this particular macro:
4. Confusing, no? Two different functions in the same computer package that do the same
thing.
