Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

678 Chapter 25

25.4 Duration Patterns

Intuitively we would expect duration to be a decreasing function of a

bond’s coupon and an increasing function of a bond’s maturity. The ﬁ rst

of these intuitions is correct, but the second is not.

The following spreadsheet shows the effect of increasing the coupon

on a bond’s duration, which—as our intuition indicated—indeed declines

as the coupon increases:

ABC D

Current date 5/21/1996 <

=DATE(1996,5,21)

Maturity, in years 21

Maturity date 5/21/2017 <

=DATE(1996+B3,5,21)

YTM 15% Yield to maturity (i.e., discount rate)

Coupon 4%

Face value 1,000

Duration 9.0110 <

=DURATION(B2,B4,B6,B5,1)

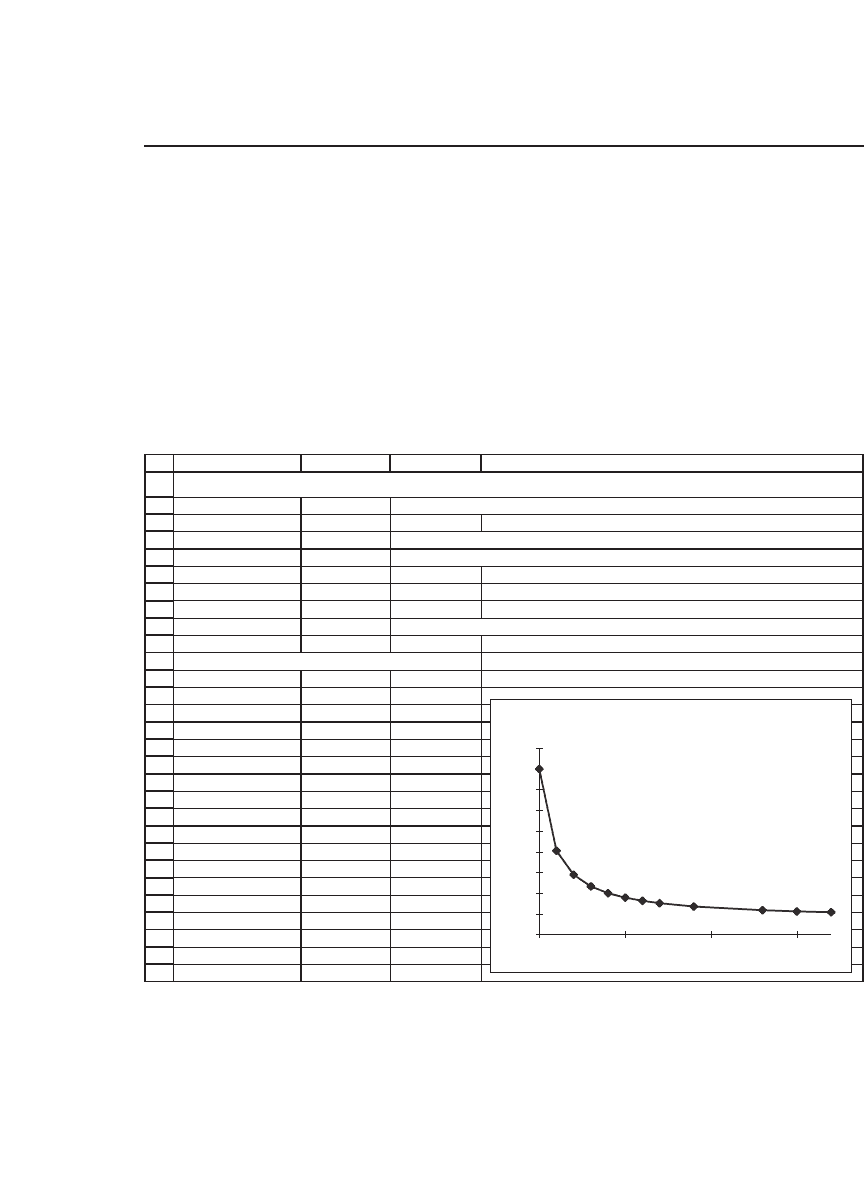
Data table: Effect of coupon on duration

9.0110 <

=B9 , data table header

0% 21.0000

1% 13.1204

Bond coupon

> 2% 10.7865

3% 9.6677

4% 9.0110

5% 8.5792

6% 8.2736

7% 8.0459

9% 7.7294

13% 7.3707

15% 7.2593

17% 7.1729

EFFECT OF COUPON ON DURATION

Effect of Coupon on Duration

Maturity = 21, YTM = 15.00%

051015

Coupon rate (%)

Duration

It is not true, however, that the duration is always an increasing func-

tion of the bond maturity:

679 Duration

25.5 The Duration of a Bond with Uneven Payments

The duration formulas that we have discussed assume that bond pay-

ments are evenly spaced. This is almost invariably the case for bonds,

except for the ﬁ rst payment. For example, consider a bond that pays inter-

est on May 1 of each of the years 1997, 1998, . . . , 2010, with repayment

of its face value on the last date. All the payments are spaced one year

apart; however, if this bond is purchased on September 1, 1996, then the

time to the ﬁ rst payment is eight months, not one year. We shall refer to

such a bond as a bond with uneven payments. In this section we discuss

two aspects of this (extremely common) problem:

•

The calculation of the duration of such a bond, when the YTM is

known. We show that the duration has a very simple formula, related to

the duration of a bond with even payments (i.e., the standard duration

formula). In the process of the discussion we develop a simpler duration

formula in Excel.

ABC D

Current date 5/21/1996 <

=DATE(1996,5,21)

Maturity, in years 21

Maturity date 5/21/2017 <

=DATE(1996+B3,5,21)

YTM 15% Yield to maturity (i.e., discount rate)

Coupon 4%

Face value 1,000

Duration 9.0110 <

=DURATION(B2,B4,B6,B5,1)

Data table: Effect of maturity on duration

9.0110 <

=B9 , data table header

11.0000

54.5163

Bond maturity

>10 7.4827

15 8.8148

20 9.0398

25 8.7881

30 8.4461

40 7.9669

50 7.7668

60 7.6977

70 7.6759

80 7.6693

EFFECT OF MATURITY ON DURATION

Effect of Coupon on Duration

Coupon rate = 4.0%, YTM = 15.00%

0 1020304050607080

Maturity

Duration

680 Chapter 25

•

The calculation of the YTM of a bond with uneven payments. This

requires a bit of trickery, and ultimately leads us to another VBA

function.

25.5.1 Duration of a Bond with Uneven Payments

Consider a bond with N payments, the ﬁ rst of which occurs at time α <

1, and the rest of which are evenly spaced. In the derivation that follows

we show that the duration of such a bond is given by the sum of two

terms:

•

The duration of a bond with N payments spaced at even intervals (i.e.,

the standard duration discussed previously).

•

α − 1

The derivation is relatively simple. Denote the payments on the bond

by C

, C

α+1

, C

α+2

, . . . , C

α+N−1

, where 0 < α < 1. The price of the bond is

given by

+−

−

+−

∑∑

()

The duration of this bond is given by

+−

∑

()

Rewrite this last expression as follows:

−

⎧

⎨

⎩

⎫

⎬

−

+−

∑∑

()

αα

⎭⎭

−

+−

−

+−

∑

()

(

α −−

⎧

⎨

⎩

⎫

⎬

⎭

+−

∑

)

()

(()1

⎧

⎨

⎩

⎫

⎬

⎭

+−

Here is an example of the calculation of the duration of a bond with

uneven periods. Recall that when there is α until the ﬁ rst payment, the

duration formula is given by

681 Duration

+−

∑

()

Here is an example of the calculation of the duration of a bond with

uneven periods. Each of the cells D10:D14 calculates the value of a term

of this formula:

AB C D

Alpha 0.3 Time until first coupon payment (in years)

N 5 Number of payments

YTM 6%

Coupon 100

Face 1,000

Bond price 1,217 <

=NPV(B4,B10:B14)*(1+B4)^(1-B2)

Period Payment t*C

/Price*(1+YTM)

0.3 100 0.0242 <

=(B10*A10)/(1+$B$4)^A10/$B$7

1.3 100 0.0990

2.3 100 0.1653

3.3 100 0.2237

4.3 1,100 3.0249

Duration 3.5371 <

=SUM(C10:C14)

Newly defined VBA function 3.5371 <

=dduration(B3,B5/B6,B4,B2)

DURATION OF BOND WITH UNEVEN PERIODS

Brute Force Calculation and Dduration function

As noted in section 25.2.1, the built-in Excel formula Duration( )

is somewhat difﬁ cult to use, because of the insertion of the dates. We

therefore write a simpler duration formula using VBA; the syntax of this

formula is DDuration(numPayments, couponRate, YTM, timeFirst):

Function dduration(numPayments, couponRate,

YTM, timeFirst)

price = 1 / (1 + YTM) ^ numPayments

dduration = numPayments / (1 + YTM) ^ _

numPayments

For Index = 1 To numPayments

price = couponRate / (1 + YTM) ^ _

Index + price

Next Index

682 Chapter 25

Our homemade formula DDuration requires only the number of pay-

ments on the bond, the coupon rate, and the time to the ﬁ rst payment α.

The use of the formula is illustrated in the previous spreadsheet picture,

in cell C17.

25.5.2 Calculating the YTM for Uneven Periods

As the preceding discussion shows, the calculation of duration requires

us to know the bond’s yield to maturity (YTM); this YTM is just the

internal rate of return of the bond’s payments and its initial price. Often

the YTM is given, but when it is not, we cannot use Excel’s IRR function

but must instead use the XIRR function.

Consider a bond that currently costs $1,123 and that pays a coupon of

$89 on January 1 of each year. On January 1, 2001, the bond will pay

$1,089, the sum of its annual coupon and its face value. The current date

is October 3, 1996. The problem in ﬁ nding the YTM of this bond is that

while most of the bond payments are spaced one year apart, there is only

0.2466 of a year until the ﬁ rst coupon payment: 0.2466 = [Date(1997,1,1)

− Date(1996,10,3)/365]. Thus we wish to use Excel to solve the following

equation:

−+

∑

0 2466 4 2466

,123

,089

YTM YTM() )

To solve this problem, we can use the Excel function XIRR:

For Index = 1 To numPayments

dduration = couponRate * Index / _

(1 + YTM) ^ Index + dduration

Next Index

dduration = dduration / price + timeFirst

- 1

End Function

683 Duration

To use the XIRR function, you ﬁ rst have to make sure that the Analy-

sis ToolPak is loaded into Excel. Go to Tools|Add-Ins. This brings up the

following menu, in which you have to make sure that Analysis ToolPak

is checked:

ABC D

Current date 3-Oct-96

Annual coupon 89 Paid January 1 for each of next 5 years

Maturity date 1-Jan-01

Face value 1,000

Price of bond 1,123

Time to first payment 0.2466 <

=(B12-B11)/365

Date Payment

3-Oct-96 -1,123

1-Jan-97 89

1-Jan-98 89

1-Jan-99 89

1-Jan-00 89

1-Jan-01 1,089

YTM 7.300% <

=XIRR(C11:C16,B11:B16)

USING XIRR TO CALCULATE THE IRR WITH

UNEVEN PAYMENTS

684 Chapter 25

You can now use XIRR, which returns the internal rate of return for

a schedule of cash ﬂ ows that is not necessarily periodic. To use this func-

tion you have to specify the list of cash ﬂ ows and the list of dates. As in

the case of the Excel function IRR, you can also provide a guess for the

IRR, although this may be left out.

25.5.3 Calculating the YTM for Uneven Payments Using a VBA Program

If you do not know the payment dates, you can use VBA to calculate

the YTM for a series of uneven payments. The following program is

composed of two functions. The ﬁ rst function, annuityvalue, calculates

the value

∑

1()

. The second function, unevenYTM, uses the simple

bisection technique to calculate the YTM of a series of uneven payments,

leaving you to choose the accuracy epsilon of the desired result.

1. There is also a function XNPV for ﬁ nding the present value of a series of payments

made at uneven dates. This function is discussed in Chapter 34.

Function annuityvalue(interest, numberPeriods)

annuityvalue = 0

For Index = 1 To numberPeriods

annuityvalue = annuityvalue + 1 / _

(1 + interest) ^ Index

Next Index

End Function

Function unevenYTM(couponRate, faceValue,

bondPrice, _

numberPayments, timeToFirstPayment, _

epsilon)

Dim YTM As Double

high = 1

low = 0

685 Duration

An illustration of the use of this function follows:

While Abs(annuityvalue(YTM, numberPayments) _

* couponRate * _

faceValue + faceValue / (1 + YTM) ^

numberPayments - _

bondPrice / (1 + YTM) ^ (1 - _

timeToFirstPayment)) >= epsilon

YTM = (high + low) / 2

If annuityvalue(YTM, numberPayments) _

* couponRate * _

faceValue + faceValue / (1 + YTM) ^ _

numberPayments - _

bondPrice / (1 + YTM) ^ (1 - _

timeToFirstPayment) > 0 Then _

low = YTM

Else

high = YTM

End If

Wend

unevenYTM = (high + low) / 2

End Function

686 Chapter 25

AB C

Coupon rate 7.90%

Face value 1,000.00

Bond price 1,123.00

Number of payments 5

Time to first payment 0.25

Epsilon 0.00001 <

Controls the accuracy of the YTM calculation

YTM 6.138% <

=unevenYTM(B3,B4,B5,B6,B7,B8)

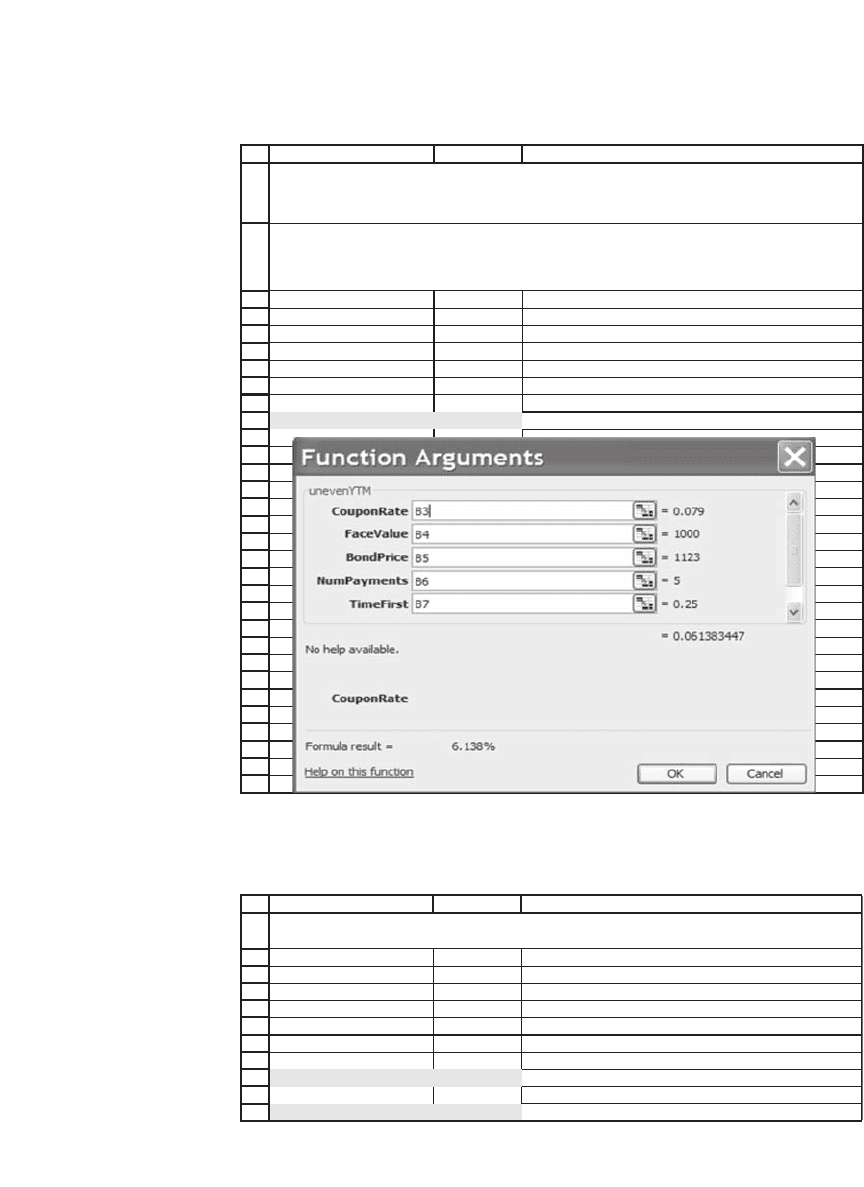
This spreadsheet illustrates the

unevenYTM

VBA function:

The syntax of this function is

unevenYTM

(CouponRate,FaceValue,BondPrice,NumPayments,TimeFirst,epsilon)

ILLUSTRATION OF CALCULATION

OF YTM OF UNEVEN PERIODS

We can, of course, use the Dduration function in conjunction with

unevenYTM to compute the duration:

AB C

Coupon rate 7.90%

Face value 1,000.00

Bond price 1,123.00

Number of payments 5

Time to first payment 0.25

Epsilon 0.00001 <

Controls the accuracy of the YTM calculation

YTM 6.138% <

=unevenYTM(B2,B3,B4,B5,B6,B7)

Duration 3.5959 <

=dduration(B5,B2,B9,B6)

USING DDURATION AND UNEVENYTM TOGETHER

687 Duration

25.6 Nonﬂ at Term Structures and Duration

In a general model of the term structure, payments at time t are dis-

counted by rate r

, so that the value of a bond is given by

∑

1()

The duration measure discussed in this chapter assumes either a ﬂ at term

structure (i.e., r

= r for all t) or a term structure that shifts in a parallel

fashion. When the term structure exhibits parallel shifts, we can write the

bond price as

∑

1()Δ

and then derive a measure of duration by taking the derivative with

respect to Δt.

A general model of the term structure should explain how the discount

rate r

for time-t payments comes about and how the rates at time t

change. This is a difﬁ cult problem, one aspect of which we discuss in

Chapter 28. A somewhat simpler problem, discussed in Chapter 27, is the

construction of a polynomial approximation to the term structure.

Does the difﬁ culty of the problem mean that the simple duration

measure we present in this chapter is useless? Not necessarily. It may be

that the Macauley duration measure gives a good approximation for

changes in bond value as a result of changes in the term structure, even

for the case when the term structure itself is relatively complex and not

ﬂ at.

In this section, we explore this possibility, using data from the ﬁ le

McCulloch_term_structures.xls, which is on the disk that accompanies

this book.

The ﬁ le contains monthly information on the term structure

of interest rates in the United States for the period 12.1946–2.87 (i.e.,

December 1946–February 1987). A typical row of this ﬁ le looks like

this:

2. A paper by Gultekin and Rogalski (1984) seems to conﬁ rm that it does.

3. The data are from McCulloch (1990). A second ﬁ le on the disk with this book, Daily

treasury yields, 1961–2006.xls gives the daily term structures.