Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

648 Chapter 23

Notes

•

In the VBA message box, use Chr(13) to start a new line.

•

Use range names in the spreadsheet to transfer values from the spreadsheet to

the VBA routine.

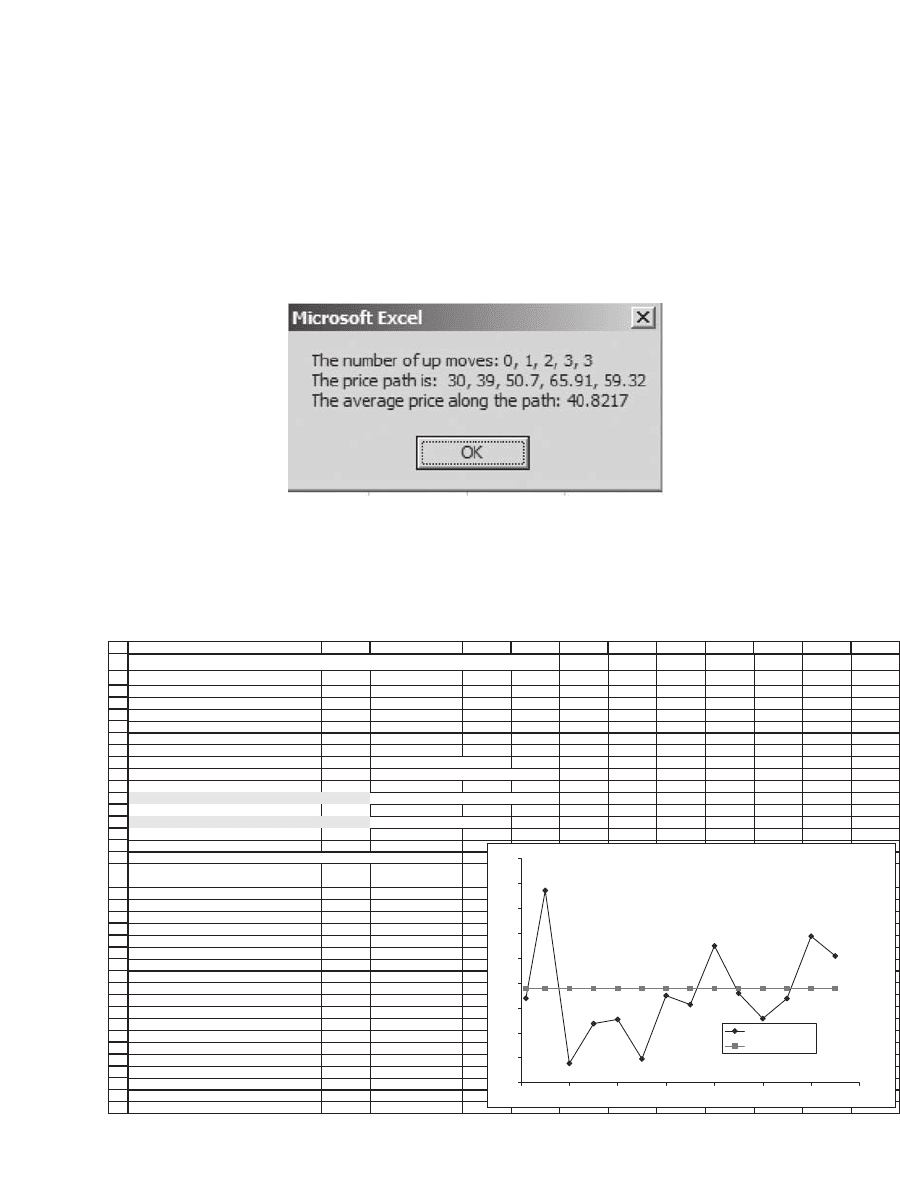
5. Repeat the last exercise. This time compute the average price of a path:

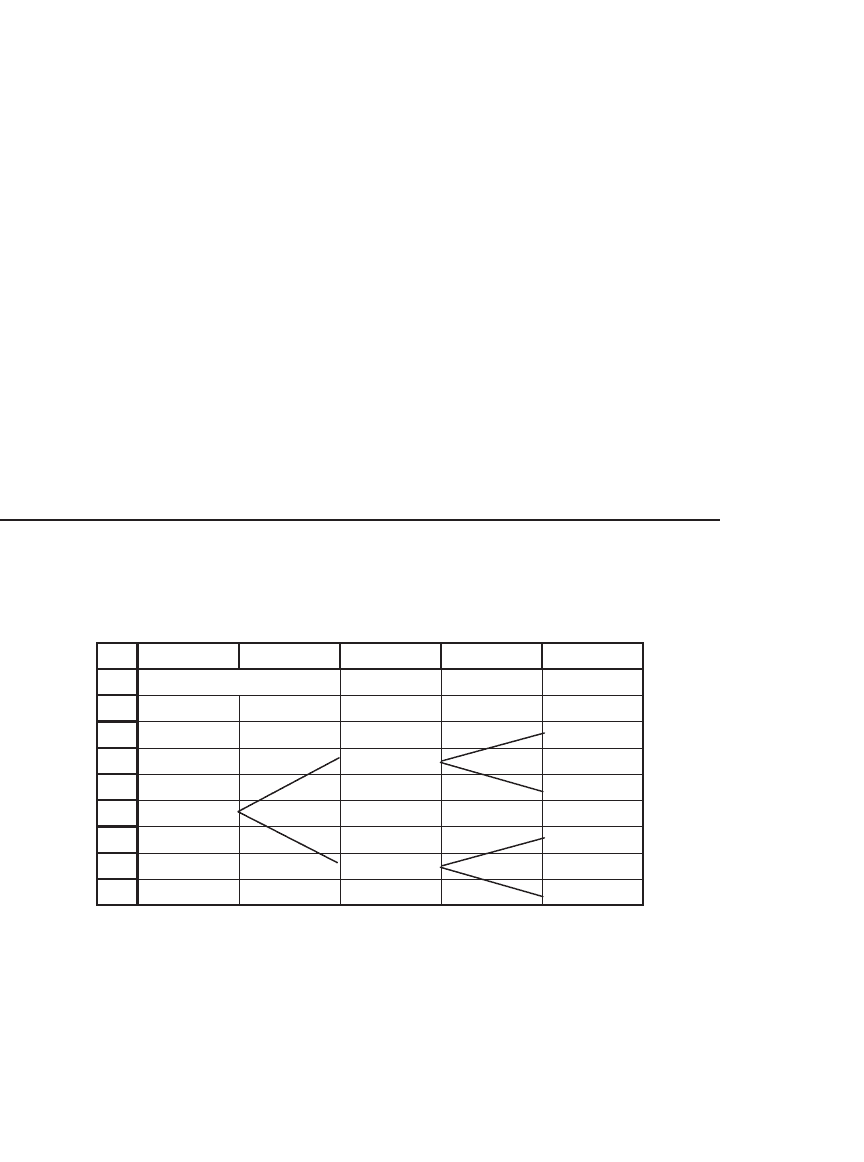
6. Use the function VanillaCall deﬁ ned in the chapter to create a Data table in which

you can see the relation between the number of runs incorporated in the function

and the Black-Scholes value of a call. Your result should look something like the

following:

LKJIHGFEDCBA

, current stock price

05ecirpesicrexe,X

%01etartseretni,r

8.0emit,T

, mean stock return

33%

, sigma--standard deviation of stock return

30%

sihthtiwdnuoragniyalpyrT--<001emittinufosnoisivid,n

elbatatadehtnideretlas'tahwsisihT--<002snuR

)01B,9B,5B,4B,7B,6B,3B,2B(llacallinav=--<6766.8llaCallinaV

)7B,4B,5B,3B,2B(llaCSB=--<2872.7llacSB

Data table: the effect of runs on the MC Vanilla call value

Monte

Carlo

Black-Scholes

Runs 8.6676 7.2782

2872.70932.7001

2872.74176.7005

2872.76779.6000,1

2872.76731.7005,1

2872.71451.7000,2

2872.75599.6005,2

2872.77942.7000,3

2872.72312.7005,3

2872.73944.7000,4

2872.78852.7005,4

2872.75751.7000,5

2872.70832.7005,5

2872.72884.7000,6

2872.77804.7005,6

MONTE CARLO PRICING OF PLAIN VANILLA CALLS

6.90

7.00

7.10

7.20

7.30

7.40

7.50

7.60

7.70

7.80

0 1,000 2,000 3,000 4,000 5,000 6,000 7,000

Monte Carlo

Black-Scholes

Real Options

24.1 Overview

The standard net present value (NPV) analysis of capital budgeting

values a project by discounting its expected cash ﬂ ows at a risk-adjusted

cost of capital. This discounted cash ﬂ ow (DCF) technique is by far the

most widely used practice for evaluating capital projects, be they acquisi-

tions of companies or the purchases of machines. However, standard

NPV analysis does not take account of the ﬂ exibility inherent in the

capital budgeting process: Part of the complexity of the capital budgeting

process is that the ﬁ rm can change its decision dynamically, depending

on the circumstances.

Here are two examples:

1. A ﬁ rm is considering replacing some of its machines with a new type

of machine. Instead of replacing all the machines together, it can ﬁ rst

replace one machine. Based on the performance of the ﬁ rst machine

replaced, the ﬁ rm can then decide whether to replace the rest of the

machines. This “option to wait” (or perhaps the “option to expand”) is

not valued in the standard NPV process. It is essentially a call option.

2. A ﬁ rm is considering investing in a project that will produce (uncer-

tain) cash ﬂ ows over time. One option—not valued in the standard NPV

framework—is to abandon the project if its performance is not satisfac-

tory. The abandonment option, as we will see, is a put option that is implicit

in many projects. It is also sometimes called the option to contract scale.

There are many other real options. In the leading book on the valua-

tion of real options, Trigeorgis (1996) lists the following common ones:

•

The option to defer or to wait when developing a natural resource or

build a plant.

•

The time-to-build option (staged investment): At each stage the invest-

ment can be reevaluated and (possibly) abandoned or expanded.

•

The option to alter operating scale (expand, contract, shut down, or

restart).

•

The option to abandon.

•

The option to switch inputs or outputs.

•

The growth option—an early investment in a project constitutes an

option to “get into the market” at a later date.

650 Chapter 24

The recognition of real options is an important extension of the NPV

techniques. However, modeling and valuing real options is more difﬁ cult

than modeling and valuing standard cash ﬂ ows by the DCF method. Our

examples in this chapter illustrate these difﬁ culties. Often it is best to

implement real options by recognizing that the DCF technique mis-

judges the value of a project because it ignores the project’s real options.

Our usual conclusion will be that real options add to the value of a

project, and that the NPV thus underestimates the true value.

24.2 A Simple Example of the Option to Expand

In this section we give a simple example of the option to expand. Con-

sider ABC Corporation, which has six widget machines. ABC is consider-

ing replacing each of the old machines with a new machine that costs

$1,000. The new machines have a ﬁ ve-year life. The anticipated cash ﬂ ows

for the new machine are as follows:

BACDEF

Year 0 1 2 3 4 5

CF of single machine -1,000 220 300 400 200 150

Discount rate for machine cash flows (risk-adjusted) 12%

Riskless discount rate 6%

Present value of machine's future cash flows 932.52 <-- =NPV(B5,C3:G3)

NPV of single machine -67.48 <-- =NPV(B5,C3:G3)+B3

THE OPTION TO EXPAND

The ﬁ nancial analyst working on the replacement project has estimated

a cost of capital for the project of 12 percent. Using these anticipated

cash ﬂ ows and the 12 percent cost of capital, the analyst has concluded

that the replacement of a single old machine by a new machine is unprof-

itable, since the NPV is negative:

−++

()

↑

1000

220

112

300

112

400

112

200

112

150

112

2345

....

TThe present valueof the machine’s future

cash flow is $932.52

 

=−67 48.

1. These cash ﬂ ows are the incremental cash ﬂ ow of replacing a single old machine by a

new machine. The computations include taxes, incremental depreciation, and the sale

of the old machine.

651 Real Options

Now comes the (real options) twist. The line manager in charge of the

widget line says, “I want to try one of the new machines for a year. At

the end of the year, if the experiment is successful, I want to replace ﬁ ve

other similar machines on the line with the new machines.”

Does this plan change our previously negative conclusion about re-

placing a single machine? The answer is yes. To see this point, we now

realize that what we have is a package:

•

Replacing a single machine today. This has an NPV of −67.48.

•

The option of replacing ﬁ ve more machines in one year. Suppose that

the risk-free rate is 6 percent. Then we view each such option as a call

option on an asset that has current value S equal to the present value of

the machine’s future cash ﬂ ows. As can be seen in cell B7, this present

value is S = 932.52. The exercise price of this option is X = 1,000. Of

course these call options can be exercised only if we purchase the ﬁ rst

machine now.

Suppose we assume that the Black-Scholes option-pricing model can

price this option. In this case we have the following:

2. What we’re really doing is pricing the cost of learning!

BACDE

Year 0 1 2 3 4 5

CF of single machine -1,000 220 300 400 200 150

Discount rate for machine cash flows (risk-adjusted) 12%

Riskless discount rate 6%

Present value of machine's future cash flows 932.52 <-- =NPV(B5,C3:G3)

NPV of single machine -67.48 <-- =NPV(B5,C3:G3)+B3

Number of machines bought next year 5

Option value of single machine purchased in one more year 143.98 <-- =B24

NPV of total project 652.39 <-- =B8+B10*B11

Black-Scholes Option-Pricing Formula

S 932.52 PV of machine CFs

X 1,000.00 Exercise price = Machine cost

r 6.00% Risk-free rate of interest

T 1 Time to maturity of option (in years)

Sigma 40% <-- Volatility

0.1753 <-- (LN(S/X)+(r+0.5*sigma^2)*T)/(sigma*SQRT(T))

-0.2247

<-- d

- sigma*SQRT(T)

N(d

)

0.5696

<--- Uses formula NormSDist(d

)

N(d

)

0.4111

<--- Uses formula NormSDist(d

)

Option value = BS call price 143.98

<-- S*N(d

)-X*exp(-r*T)*N(d

)

THE OPTION TO EXPAND

652 Chapter 24

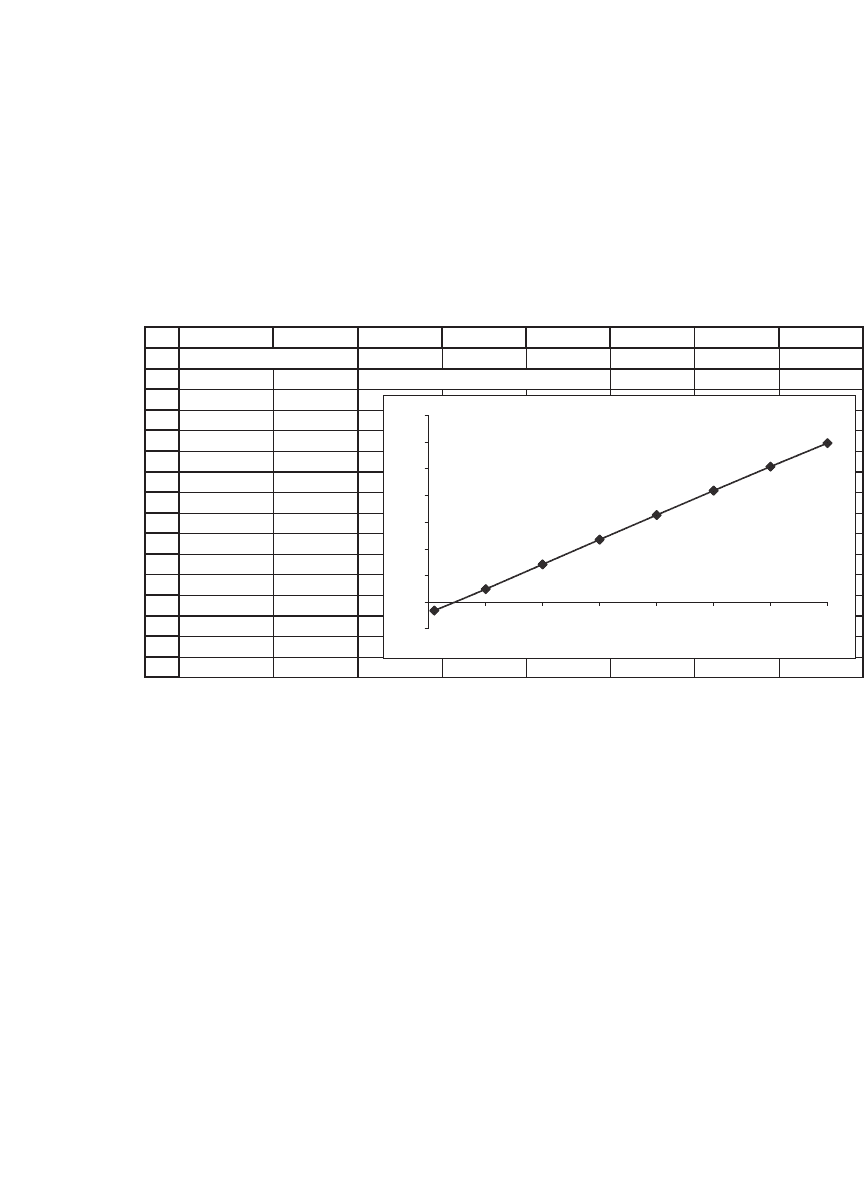
As cell B12 shows, the value of the whole project is 652.39.

Our conclusion: Buying one machine today, and knowing that we have

the option to purchase ﬁ ve more machines in one year is a worthwhile

project. One critical element here is the volatility. The lower the volatility

(i.e., the lower the uncertainty), the less worthwhile this project is:

BCDEFGHI

652.39 <-- =B12 , data table header

1% -63.48

10% 97.16

20% 283.09

30% 468.40

40% 652.39

50% 834.59

60% 1,014.54

70% 1,191.81

Data Table

Project Value as Function of Sigma

-200

200

400

600

800

1,000

1,200

1,400

010203040506070

Sigma (%)

This outcome is not very surprising: The value of the project as a whole

comes from our uncertainty about the actual cash ﬂ ows one year from

now. The less is this uncertainty (measured by σ), the less valuable is the

project.

24.2.1 Sidebar: Is Black-Scholes the Appropriate Valuation Tool for Real

Options?

The answer is almost certainly no: Black-Scholes is not the appropriate

tool. However, the Black-Scholes model is by far the most numerically

tractable (i.e., easiest) model we have for valuing options of any kind. In

valuing real options we often use the Black-Scholes model, realizing that

at best it can give an approximation to the actual option value. Such is

life.

Nevertheless, you should realize that the assumptions of the Black-

Scholes option valuation model—continuous trading, constant interest

653 Real Options

rate, no exercise before ﬁ nal option maturity—are not really appropriate

to the real options considered in this chapter. In many cases real options

involve what, in a securities option context, would be considered

dividend-paying securities and/or early exercise. Here are two

examples:

•

The staged-investment real option, when we have the opportunity to

expand or contract the investment over time, is intrinsically an option

with early exercise.

•

When an option to abandon an investment exists, as long as the invest-

ment is still in place and not abandoned, it continues to pay “dividends,”

in the form of cash ﬂ ows.

We can only hope is that the Black-Scholes model gives an approxima-

tion to the option value intrinsic in the real options.

24.3 The Abandonment Option

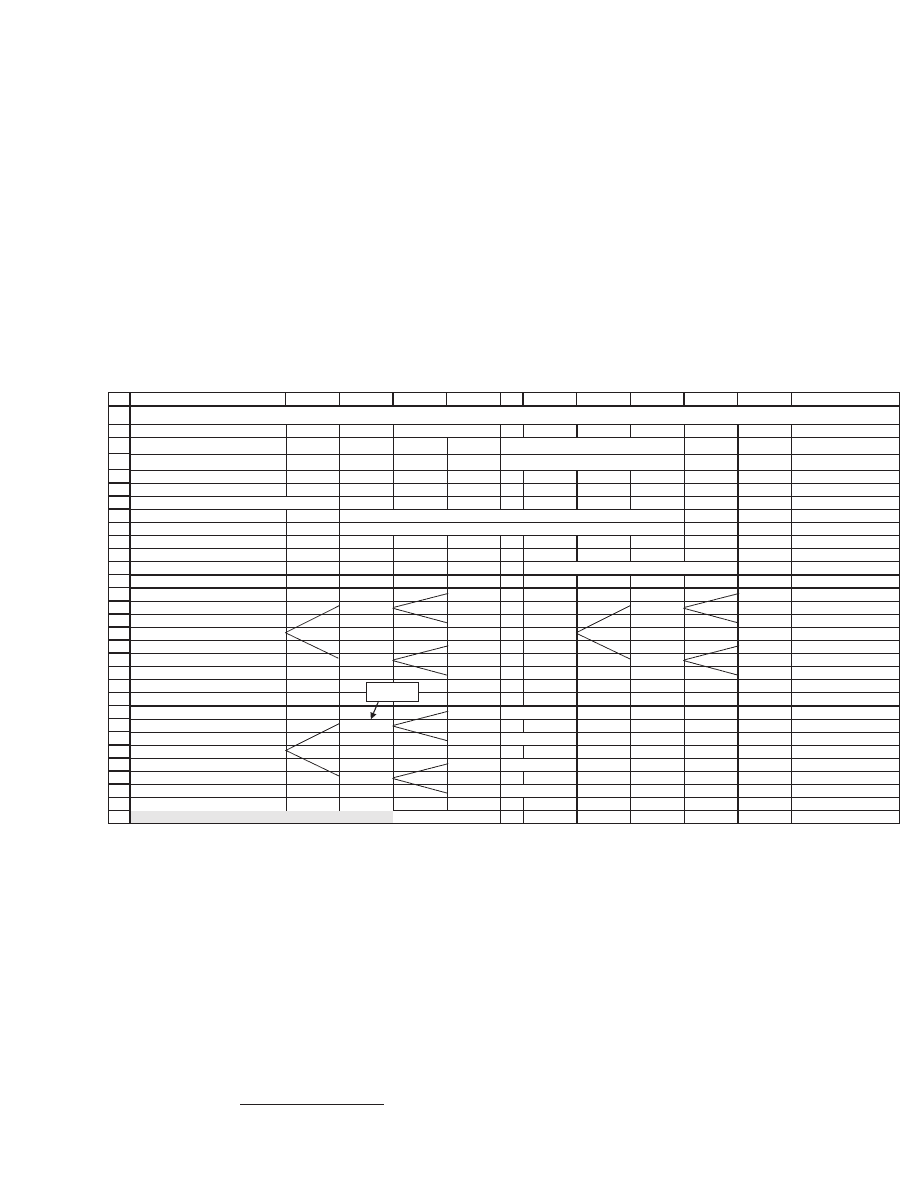
Consider the following capital budgeting project:

ABCDE

Project cash flows

150

100

-50

-60

As you can see, the initial cost of this project is $50. In one period the

project will produce cash ﬂ ows of either $100 or −$50; that is, under

certain circumstances, it will lose money. Two periods hence the project

again has chances of either losing money (in the worst case) or making

money.

654 Chapter 24

24.3.1 Valuing the Project

In order to value the project, we use the state prices from option pricing.

The state price q

is the price today of $1 to be paid in the succeeding

period in the “up” state; and the price q

is the price today of $1 to be

paid in the “down” state. The following spreadsheet fragment shows all

the relevant details, leading to a project valuation of −$29.38 (implying

rejection of the project):

ABCDEFGHIJKL

Market data State prices

Expected market return 12%

0.3087 <-- =(1+B5-B9)/((1+B5)*(B8-B9))

Sigma of market return 30%

0.6347 <-- =(B8-1-B5)/((1+B5)*(B8-B9))

Risk-free rate 6%

One-period "up" and "down" of market

Up 1.521962 <-- =EXP(B3+B4) , note that a valid alternative is 'Up' = EXP(B4)

Down 0.83527 <-- =EXP(B3-B4) , note that a valid alternative is 'Down' = EXP(-B4)

Project cash flows State-dependent present value factors

150 0.0953 <-- =E3^2

100 0.3087

80 0.1959 <-- =E3*E4

-50 1

80 0.1959 <-- =E3*E4

-50 0.6347

-60 0.4028 <-- =E4^2

State-by-state present value

14.2981 <-- =E14*K14

30.8740

15.6755 <-- =E16*K16

-50

15.6755 <-- =E18*K18

-31.7328

-24.1673 <-- =E20*K20

Net present value

-29.38 <-- =SUM(A23:E29)

PRICING AN ABANDONMENT OPTION

=C15*I15

The methodology is to calculate state-dependent present value factors

(discussed later) and to multiply these factors times the individual state-

dependent cash ﬂ ows. Each node of the tree is discounted by the relevant

state price for the node; for example, the cash ﬂ ow of 80 that occurs at

date 2 is discounted by q

. The NPV of the project is the sum of all

the discounted cash ﬂ ows plus the initial cost (cell B31).

3. See section 24.3.4 on how to calculate these state prices.

655 Real Options

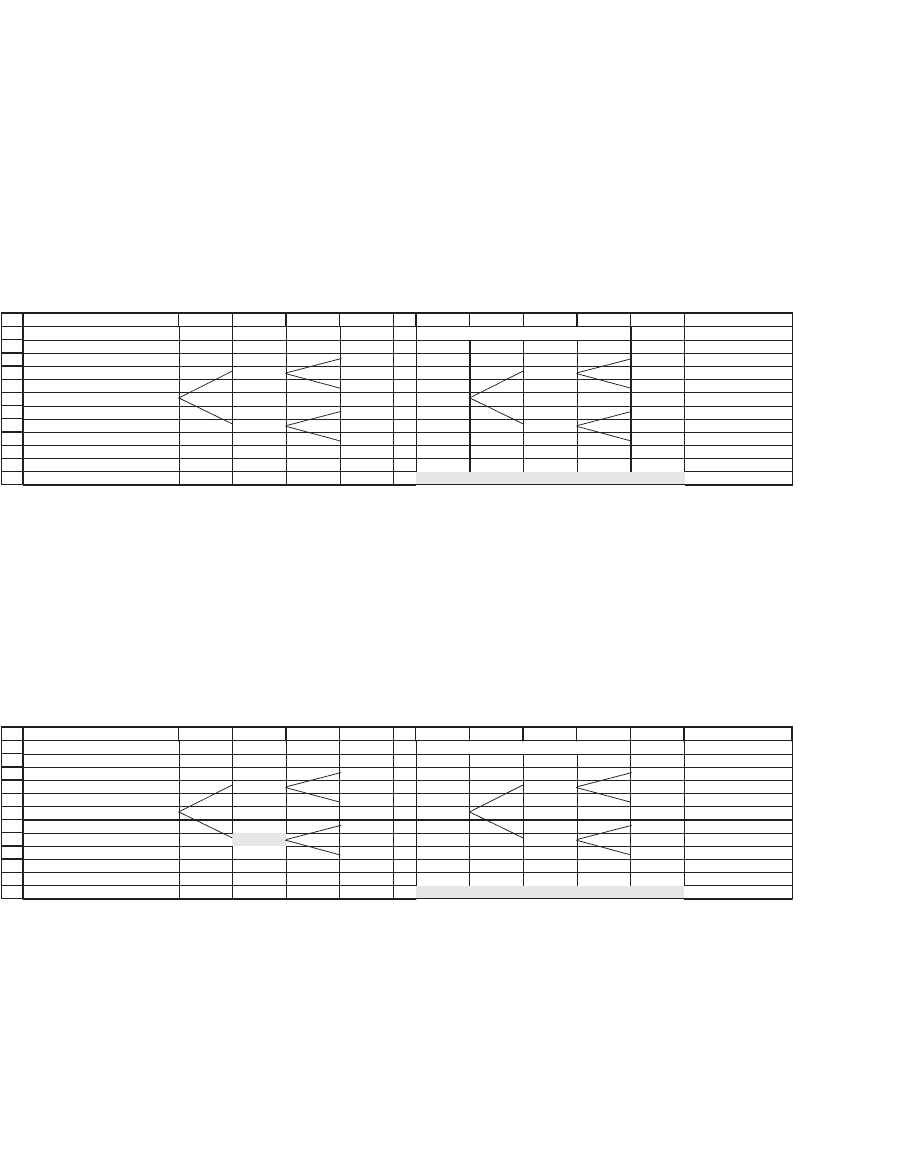
24.3.2 The Abandonment Option Can Enhance Value

Now suppose that we can abandon the project at date 1 if its cash ﬂ ow

“threatens” to be −50; suppose, furthermore, that this abandonment

means that all subsequent cash ﬂ ows will also be zero. As the next picture

shows, this option to abandon the project enhances its value:

ABCDEFGHIJKL

Cash flows with abandonment Present value with abandonment

150 14.2981 <-- =E36*K14

100 30.8740

80 15.6755 <-- =E38*K16

-50 -50

Present value with abandonment 10.85 <-- =SUM(G36:K42)

Thinking about this topic further, it is clear that it might even be worth-

while to pay to abandon the project. Here’s what the project looks like

when we pay $10 to abandon it in the troublesome state (this payment

can be thought of as representing the cost of closing down a facility, for

example):

ABCDEFGHIJKL

Cash flows with abandonment Present value with abandonment

150 14.2981 <-- =E36*K14

100 30.8740

80 15.6755 <-- =E38*K16

-50 -50

-10 -6.3466

Present value with abandonment 4.50 <-- =SUM(G36:K42)

24.3.3 Abandonment When We Sell the Equipment

Another possibility is, of course, that “abandonment” means selling the

equipment. In this case there might even be a positive cash ﬂ ow from

abandonment. As an example, suppose that we can sell the asset for

$15:

656 Chapter 24

24.3.4 Determining the State Prices

The method we have used to determine the state prices was explained

in greater detail in Chapter 17. We assume that in each period the market

portfolio (by which we mean some large, diversiﬁ ed stock market port-

folio such as the S&P 500) either moves “up” or “down”; the size of these

moves is determined by the mean return μ of the market portfolio and

by the standard deviation σ of the market portfolio’s returns. Assuming

that the returns on the market portfolio have mean μ = 12 percent and

standard deviation of returns σ = 30 percent, we have—in the preceding

examples—calculated

Up exp[ ] Down exp[ ]=+= =−=μσ μσ153 084., .

Denote by q

the price today for one dollar in the up state in one period,

and denote by q

the price today for one dollar in the down state in one

period. Then—as explained in Chapter 17—the state prices are calcu-

lated by solving the following system of linear equations:

=∗ +∗

Up Down

The solution to this system of equations is

−

∗−

−

∗−

Down

Up Down

Up Down()

()

This method is illustrated in the spreadsheet from section 24.3.1:

ABCDEFGHIJKL

Cash flows with abandonment Present value with abandonment

150 14.2981 <-- =E36*K14

100 30.8740

80 15.6755 <-- =E38*K16

-50 -50

15 9.5198

Present value with abandonment

20.37 <-- =SUM(G36:K42)

657 Real Options

24.3.5 Alternative State-Price Determinations

An alternative method of calculating the state prices is to try to match

them to the project’s cost of capital. Reconsider the project discussed

previously, and suppose that the actual probability of each state’s occur-

rence is

. Furthermore, suppose that the risk-free rate is 6 percent.

Finally, assume that the project’s discount rate—if it has no options

whatsoever—is 22 percent. Then we can calculate the project’s NPV

without real options as 12.48:

ABCDEFGH

Market data State prices

Expected market return 12%

0.3087 <-- =(1+B5-B9)/((1+B5)*(B8-B9))

Sigma of market return 30%

0.6347 <-- =(B8-1-B5)/((1+B5)*(B8-B9))

Risk-free rate 6%

One-period "up" and "down" of market

Up 1.521962 <-- =EXP(B3+B4) , note that a valid alternative is 'Up' = EXP(B4)

Down 0.83527 <-- =EXP(B3-B4) , note that a valid alternative is 'Down' = EXP(-B4)

ABCDEFGH

Project cost of capital 22%

<-- This is the discount rate for the project if it has

no options

Risk-free rate 6%

Project cash flows

150

100

-50

-60

Project expected cash flows

: Assumes equal state probabilities

Year 0 1 2

Expected CF -50 25 62.5

Project NPV 12.48 <-- =NPV(B2,C17:D17)+A9

State prices

0.4241 <-- =1/(1+B3)-B23

0.5193 <-- Determined by Solver

MATCHING THE STATE PRICES TO THE COST OF CAPITAL

=AVERAGE(C7:C1)

=AVERAGE(E6:E12)

In cells B22 and B23 we look for state prices q

and q

that have two

properties: