Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

668 Chapter 24

3. Consider the project whose cash ﬂ ows are as follows:

ABCDEFGH

Project cash flows

169

State prices

130

0.3000

0.5000

-100

-90

a. Using the state prices, value the project.

b. Suppose that at date 2 the project can be abandoned at no cost. What does this

fact do to its value?

c. Suppose that at any time the project can be sold for $100. Show the tree of cash

ﬂ ows and value the project.

4. Suppose that the market portfolio has mean μ = 15 percent and standard deviation

σ = 20 percent.

a. If the risk-free rate of interest is 8 percent, calculate the one-period state prices

for an up and a down state.

b. Show the effect (in a data table) of the risk-free rate on the state prices.

c. Show the effect of the σ on the state prices.

5. Consider the following cash ﬂ ows:

ABCD

Project cash flows

180

130

-50

-100

a. If the cost of capital is 30 percent and the risk-free rate is 5 percent, ﬁ nd the state

prices that match the project’s NPV.

b. If there exists an abandonment option so that we can change all negative cash

ﬂ ows to zero, value the project.

Bonds

Chapters 25–28 cover topics related to bonds and term structure.

Chapters 25 and 26 concentrate on the classic duration and immuniza-

tion formulations. In Chapter 25 we develop the basic Macauley duration

concept. Excel’s Duration( ) formula is somewhat cumbersome to use;

we use VBA to build a new, easier-to-use formula. Chapter 26 discusses

the use of duration to immunize bond portfolios. Chapter 27 shows how

to model the term structure using a polynomial approximation. These

approximations are in wide use and appear to work well for certain

purposes. Chapter 28 uses a Markov process and much information

about default probabilities and bond recovery ratios to model the

expected rate of return on a risky corporate bond.

Duration

25.1 Overview

Duration is a measure of the sensitivity of the price of a bond to changes

in the interest rate at which the bond is discounted. It is widely used as

a risk measure for bonds—the higher a bond’s duration, the more risky

it is. In this chapter we consider a basic duration measure—Macauley

duration—which is deﬁ ned for the case when the term structure is ﬂ at.

In Chapter 26 we examine the uses of duration in immunization

strategies.

Consider a bond with payments C

, where t = 1, . . . , N. Ordinarily, the

ﬁ rst N − 1 payments will be interest payments, and C

will be the sum

of the repayment of principal and the last interest payment. If the term

structure is ﬂ at and the discount rate for all of the payments is r, then

the bond’s market price today will be

∑

1()

The Macauley duration measure (throughout this chapter and the next,

when we use the word “duration” we shall always refer to this measure)

is deﬁ ned as

∑

1()

In section 25.4 we will consider the meaning of this formula. Before

doing so, however, we show how to calculate the duration in Excel.

25.2 Two Examples

Consider two bonds. Bond A has just been issued. Its face value is $1,000,

it bears the current market interest rate of 7 percent, and it will mature

in 10 years. Bond B was issued ﬁ ve years ago, when interest rates were

higher. This bond has $1,000 face value and bears a 13 percent coupon

rate. When issued, this bond had a 15-year maturity, so its remaining

maturity is 10 years. Since the current market rate of interest is 7 percent,

Bond B’s market price is given by

672 Chapter 25

(. )

130

107

1 000

107

,421.41 =+

∑

It is worthwhile calculating the duration of each of the two bonds (just

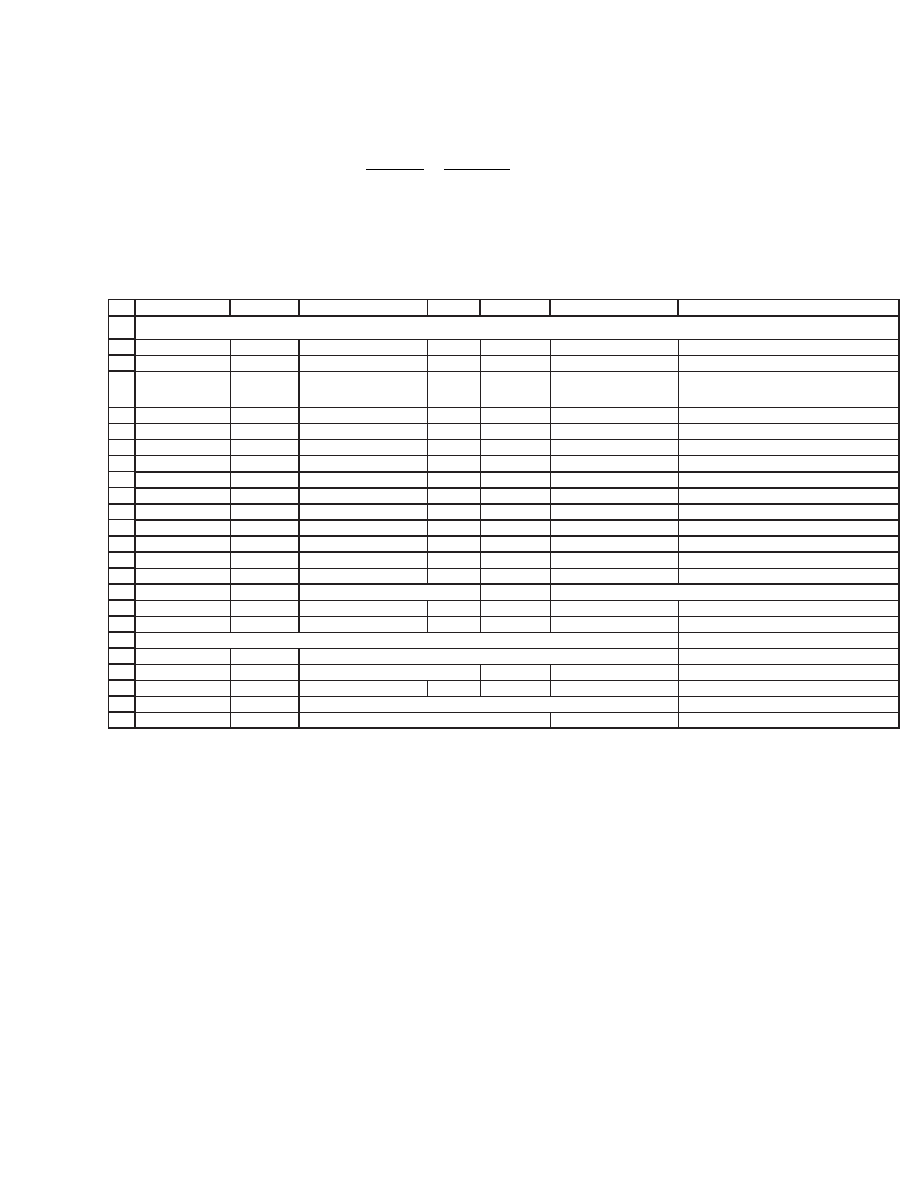
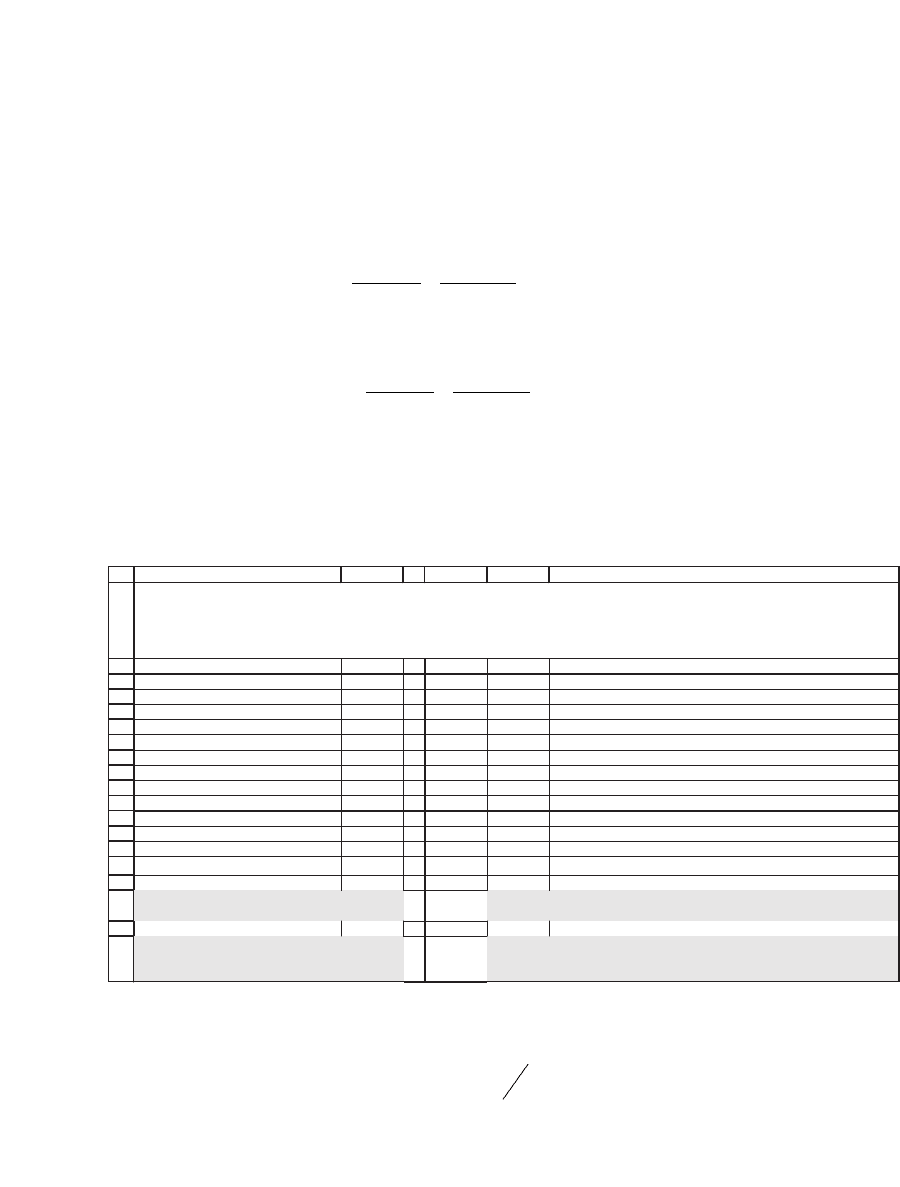
once!) the long way. We set up a table in Excel:

AB C DE F G

YTM 7%

Year C

t,A

t*C

t,A

Price

*(1+YTM)

t,B

t*C

t,B

Price

*(1+YTM)

1 70 0.0654 130 0.0855 <

=$A5*E5/(E$16*(1+$B$2)^$A5)

2 70 0.1223 130 0.1598 <

=$A6*E6/(E$16*(1+$B$2)^$A6)

3 70 0.1714 130 0.2240

4 70 0.2136 130 0.2791

5 70 0.2495 130 0.3260

6 70 0.2799 130 0.3657

7 70 0.3051 130 0.3987

8 70 0.3259 130 0.4258

9 70 0.3427 130 0.4477

10 1,070 1,130

Bond price 1,000.00 <

=NPV(B2,B5:B14) 1,421.41 <

=NPV(B2,E5:E14)

Duration 7.5152 <

=SUM(C5:C14) 6.7535 <

=SUM(F5:F14)

Using the Excel function Duration and the "home-made" function Dduration

Bond A 7.5152 <

=DURATION(DATE(1996,12,3),DATE(2006,12,3),7%,B2,1)

7.5152 <

=dduration(A14,7%,B2,1)

Bond B 6.7535 <

=DURATION(DATE(1996,12,3),DATE(2006,12,3),13%,B2,1)

6.7535 <

=dduration(A14,13%,7%,1)

BASIC DURATION CALCULATION

4.04135.4393

As might be expected, the duration of bond A is longer than that of bond

B, since the average payoff of bond A takes longer than that of bond B.

To look at this another way, the net present value of bond A’s ﬁ rst-year

payoff ($70) represents 6.54 percent of the bond’s price, whereas the net

present value of bond B’s ﬁ rst-year payoff ($130) is 8.55 percent of its

price. The ﬁ gures for the second-year payoffs are 6.11 percent and 7.99

percent, respectively. (For the second-year ﬁ gures, you have to divide the

appropriate line of the spreadsheet by 2, since in the duration formula

each payoff is weighted by the period in which it is received.)

25.2.1 Using the Excel Duration Formula

Excel has two duration formulas, Duration( ) and MDuration( ). MDura-

tion—somewhat inaccurately termed Macauley duration by Excel—is

deﬁ ned as

673 Duration

MDuration

Duration

Yield to maturity

Number of coupon payments p

eer year

⎛

⎝

⎜

⎞

⎠

⎟

Both formulas have the same syntax; for example, for Duration( ) the

syntax is as follows:

Duration(settlement, maturity, coupon, yield, frequency, basis)

where

settlement is the settlement date (i.e., the purchase date) of the bond.

maturity is the bond’s maturity date.

coupon is the bond’s coupon.

yield is the bond’s yield to maturity.

frequency is the number of coupon payments per year.

basis is the “day count basis” (i.e., the number of days in a year). This is

a code between 0 and 4:

0 or omitted US (NASD) 30/360

1 Actual/actual

2 Actual/360

3 Actual/365

4 European 30/360

The Duration formula gives the standard Macauley duration. The

MDuration formula can be used in calculating the price elasticity of the

bond (see section 25.3.2). These two duration formulas may require a bit

of trickery to implement, because they demand a date serial number for

both the settlement and the maturity. In the preceding spreadsheet

picture, the Excel formula is implemented in cell C20 by assuming that

bond A’s settlement date (for our purposes, the current date) is Decem-

ber 3, 1996, and that the bond’s maturity date is December 3, 2006. The

choice of dates is arbitrary. The last parameter of the Excel duration

formula, which gives the basis, is optional and could be omitted.

The insertion of serial date formats in the Excel Duration formula is

often unhandy. Later in this chapter we use VBA to deﬁ ne a simpler

674 Chapter 25

duration formula that overcomes this problem and that also computes

the duration of a bond when bond payments are unevenly spaced. This

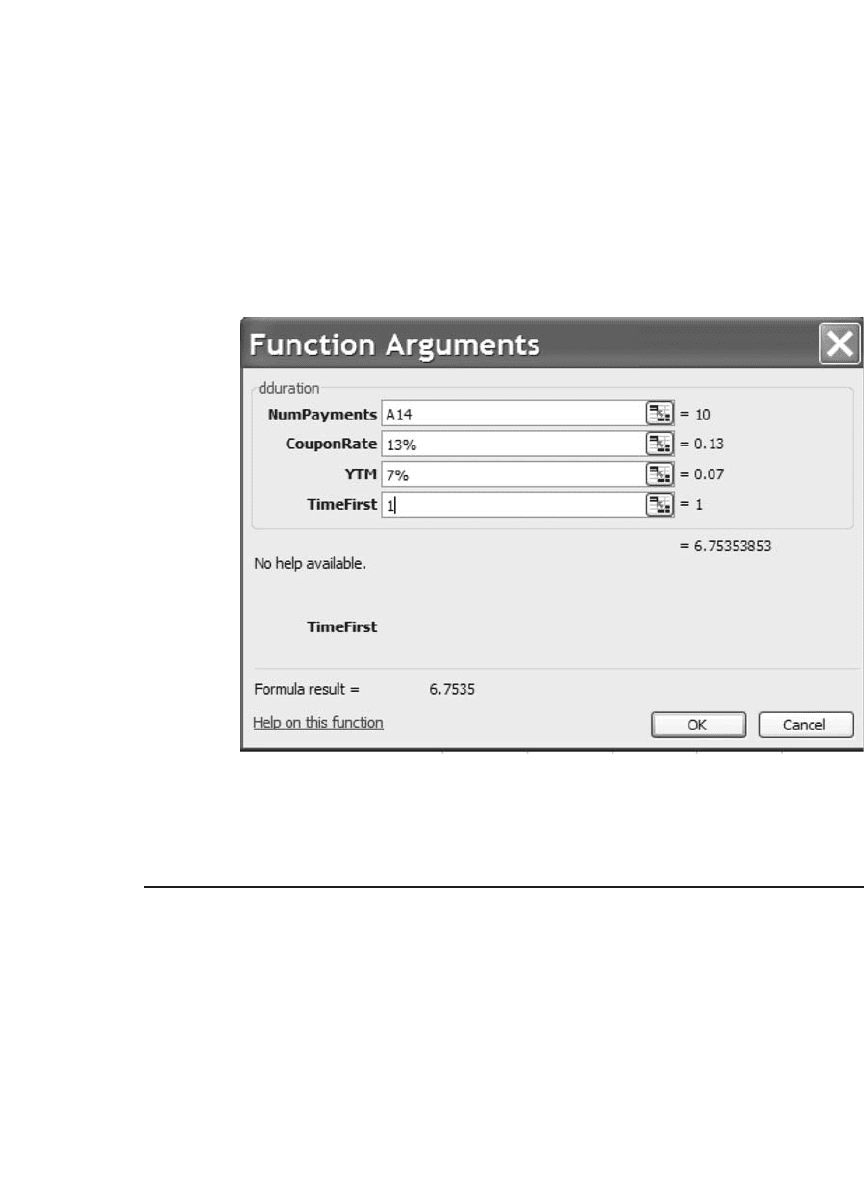
“homemade” duration formula is called Dduration. The programming

aspects of this function are discussed in section 25.5.1. The previous

spreadsheet illustrates this function in cells B21 and B24. The dialogue

box for Dduration’s computation of the duration of bond B follows:

The parameter TimeFirst is the time from the bond purchase date until

the ﬁ rst payment. For the examples of bond A and bond B this parameter

is 1.

25.3 What Does Duration Mean?

In this section we present three different meanings of duration. Each is

interesting and important in its own right.

25.3.1 Duration as the Time-Weighted Average of the Bond’s Payments

As originally deﬁ ned by Macauley (1938), duration is the time-weighted

average of the bond’s payments. Rewrite the duration formula as

follows:

675 Duration

⎡

⎣

⎢

⎤

⎦

⎥

∗

∑∑

() ()

The bracketed terms

()1+

⎡

⎣

⎢

⎤

⎦

⎥

sum to 1. This fact follows from the deﬁ -

nition of the bond price; each of these terms is the proportion of the

bond’s price represented by the payment at time t. In the duration

formula, each of the terms

()1+

⎡

⎣

⎢

⎤

⎦

⎥

is multiplied by its time of occur-

rence: Thus the duration is the time-weighted average of the bond’s dis-

counted payments as a proportion of the bond’s price.

25.3.2 Duration as the Bond’s Price Elasticity with Respect to Its Discount Rate

Viewing duration as the bond’s price elasticity with respect to its dis-

count rate explains why the duration measure can be used to measure

the bond’s price volatility; it also shows why duration is often used as a

risk measure for bonds. To derive this interpretation, we take the deriva-

tive of the bond’s price with respect to the current interest rate:

−

∑

1()

A little algebra shows that

−

=−

∑

11()

This formula transforms into two useful interpretations of duration:

•

First, duration can be regarded as the elasticity of the bond price

with respect to the discount factor, where by “discount factor” we mean

1 + r:

dP P

dr r

Percent change in bond price

Percent change in discou1+

)

nnt factor

=−D

•

Second, we can use duration to measure the price volatility of a bond

by rewriting the previous equation as

=−

676 Chapter 25

To show this interpretation of duration in a spreadsheet, we go back

to the examples of the previous section. Suppose that the market interest

rate rises by 10 percent, from 7 percent to 7.7 percent. What will happen

to the bond prices? The price of bond A will be

(. )

952 39

1 077

∑

,000

(1.077)

A similar calculation shows the price of bond B to be

(. )

130

1 077

,360.50

,000

(1.077)

∑

As predicted by the price-volatility formula, the changes in the bond

prices are approximated by ΔP ≅ −DPΔr/(1 + r). To see this relationship,

work out the numbers for each bond:

BACDE F

Discount rate 7%

Bond A Bond B

Coupon rate 7% Coupon 13%

Face value 1,000 Face value

1,000

Maturity 10 Maturity 10

Price 1,000.00 Price 1,421.41 <

=PV($B$2,E7,-E5*E6)+E6/(1+$B$2)^E7

Duration 7.5152 Duration 6.7535 <

=DURATION(DATE(1996,1,1),DATE(2006,1,1),E5,B2,1)

New discount rate 7.70%

New price 952.39 1,360.50 <

=PV($B$12,E7,-E5*E6)+E6/(1+$B$12)^E7

Change in price

Actual 47.61 60.92 <

=E9-E13

Using duration as approximation

≈

- Duration *Price*

r/(1+r)

49.17 62.80 <

=-E10*E9*($B$2-$B$12)/(1+$B$2)

Using MDuration

49.17 62.80

=-($B$2-

$B$12)*E9*MDURATION(DATE(1996,1,1),DATE(2006,1,1),E5,

$B$2,1)

DURATION AS PRICE ELASTICITY

The change in the bond price can be approximated by

- Duration*Price*

r/(1+r)

Note row 19 of the spreadsheet: Instead of using the Excel Duration

function and multiplying by

Δr

r()1+

, we could have used the MDura-

tion function and multiplied by Δr.

677 Duration

25.3.3 Babcock’s Formula: Duration as the Convex Combination of Bond Yields

A third interpretation of duration is Babcock’s (1985) formula, which

shows that duration is a weighted average of two factors:

PVIF r N r=−

⎛

⎝

⎞

⎠

+∗+11()(),,

where the “current yield” of the bond is

y =

Bond coupon

Bond price

and the present value of an N-period annuity is

PVIF r N

()

, =

∑

Babcock’s formula gives two useful insights into the duration measure:

•

Duration is a weighted average of the maturity of the bond and of (1

+ r) times the PVIF associated with the bond. (Note that the PVIF is

given by the Excel formula PV(r,N,-1).)

•

In many cases the current yield of the bond, y, is not greatly different

from its yield to maturity r. In these cases, duration is not very different

from (1 + r)PVIF.

Unlike the two previous interpretations, Babcock’s formula holds only

for the case of a bond with constant coupon payments and single repay-

ment of principal at time N; that is, the formula does not extend to the

case where the payments C

differ over time.

Here’s an implementation of Babcock’s formula for bond B:

AB C

N, bond maturity 10

%7,r

C, bond coupon 13%

Face value 1,000

Price 1,421.41 <

=PV(B3,B2,-B4*B5)+B5/(1+B3)^B2

Current yield 9.15% <

=B4*B5/B6

PVIF(r,N) 7.0236 <

=PV(B3,B2,-1)

Two duration formulas

Babcock's formula 6.7535 <

=B2*(1-B7/B3)+B7/B3*B8*(1+B3)

Standard formula 6.7535 <

=DURATION(DATE(1995,1,1),DATE(2005,1,1),B4,B3,1)

BABCOCK'S FORMULA FOR DURATION

Duration is convex combination of current-yield and present-value factors:

D = N*y/r + (1 - y/r) * PVIF(N,r,-1)*(1+r)