Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

618 Chapter 23

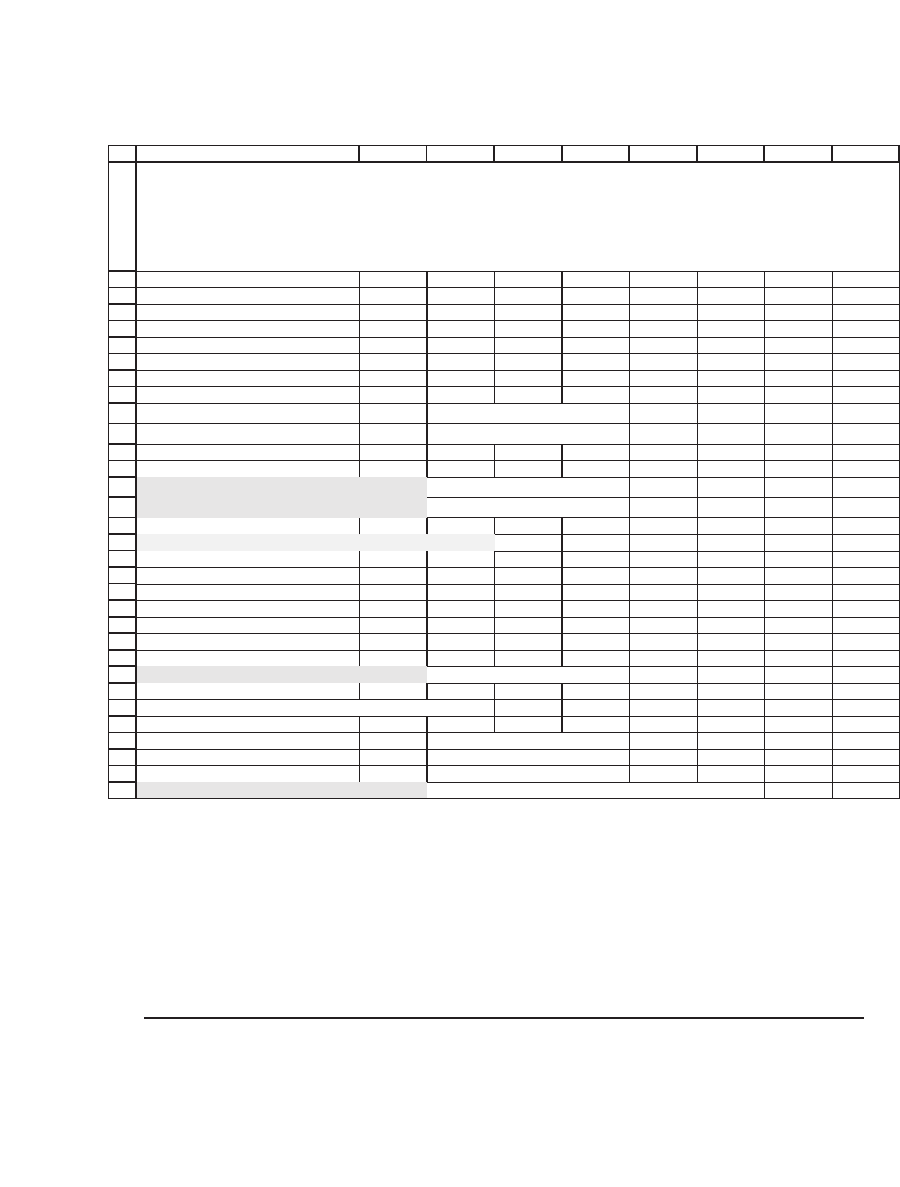
The average discounted payoff (cell B25) is 8.3055. This value is

random, meaning it will change each time we press F9 to produce a new

set of random paths. Monte Carlo methods imply that for even more

paths we would converge to the actual option price of 8.8707. In the next

section we show that the Monte Carlo method eventually produces con-

vergence to this price.

23.4 Monte Carlo Plain-Vanilla Call Pricing Converges to Black-Scholes

Now that we understand the principles, we extend our logic. We write a

VBA routine that prices a plain-vanilla call using Monte Carlo methods

under conditions that converge to Black-Scholes pricing.

BACDEFGH

Initial stock price 50

5X0

Up 1.4

Down 0.9

1R.05

State prices

0.2857 <-- =(B7-B6)/(B7*(B5-B6))

0.6667 <-- =(B7-B6)/(B7*(B5-B6))

Risk-neutral probabilities

0.3000 <-- =(B7-B6)/(B7*(B5-B6))

0.7000 <-- =(B7-B6)/(B7*(B5-B6))

First period, up (1) or down (0)? 0 0 1 0 1 0 0 0

Second period, up (1) or down (0)? 00100001

Total ups

00201001

Terminal stock price

40.5 40.5 98 40.5 63 40.5 40.5 63

Option payoff

004801300

Average discounted payoff 8.3055

<-- =AVERAGE(23:23)/R_^2

Computing the actual option price with state prices

Payoffs

Top 48 <-- =MAX(B2*up^2-B3,0)

Middle 13 <-- =MAX(B2*up*down-B3,0)

Bottom 0 <-- =MAX(B2*down^2-B3,0)

Actual option price 8.8707

<-- =q_up^2*B29+2*q_up*q_down*B30+q_down^2*B31

Random paths and the Monte Carlo price

SIMPLE SIMULATION: A TWO-DATE MODEL

As many price paths as there are columns

Pressing F9 runs the simulation and will change the value in cell B25

This value should be compared to the actual option price in cell B32

619 Using Monte Carlo Methods for Option Pricing

Our basic setup is as follows: We price a European call on a stock

whose current price is S

. The option’s exercise price is X, and the time

to maturity of the option is T. We assume that the stock price is lognor-

mally distributed with mean μ and standard deviation σ.

To price the call using Monte Carlo,

•

We divide the unit time interval into n divisions. Therefore, Δt = 1/n.

•

For each Δt, we deﬁ ne

ΔΔ

tt=+exp[ ]μσ

and

Down

Δt

ΔΔtt−exp[ ]μσ

. The interest rate on the interval Δt is R

Δt

= exp[rΔt].

•

Therefore, the state prices and risk-neutral probabilities are given by

tt t

−

ΔΔ

ΔΔ Δ

ΔΔ

ΔΔ Δ

Down

Up Down

Up Down()

()

πππ

−

=−

ΔΔ

Down

Up Down

•

Since the time to maturity of the option is T, the price path to T

requires m = T/Δt periods. A price path of length m is created by deter-

mining the Up or Down move of the stock as a function of a random

number between 0 and 1 and the risk-neutral probability π

. As discussed

in the example of section 23.3, if the random number is greater than π

the stock makes an Up move; otherwise it makes a Down move.

23.4.1 A VBA Routine

The VBA routine that follows deﬁ nes a function VanillaCall. This func-

tion requires as inputs the variables mentioned previously. The variable

Runs is the number of random price paths created; these paths are aver-

aged to determine the Monte Carlo value of the call:

Function VanillaCall(S0, Exercise, Mean, Sigma,

Interest, _

Time, Divisions, Runs)

deltat = 1 / Divisions

interestdelta = Exp(Interest * deltat)

up = Exp(Mean * deltat + Sigma * Sqr(deltat))

down = Exp(Mean * deltat - Sigma * Sqr(deltat))

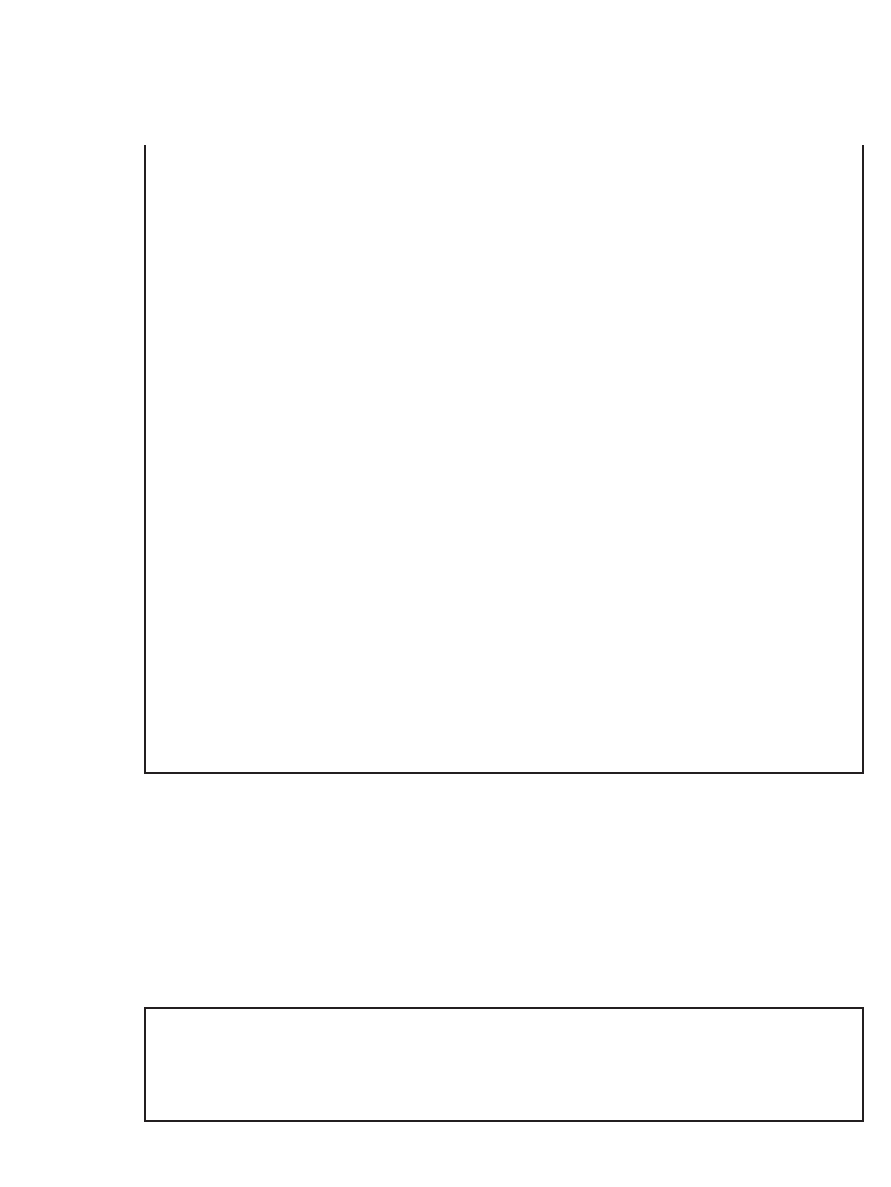
620 Chapter 23

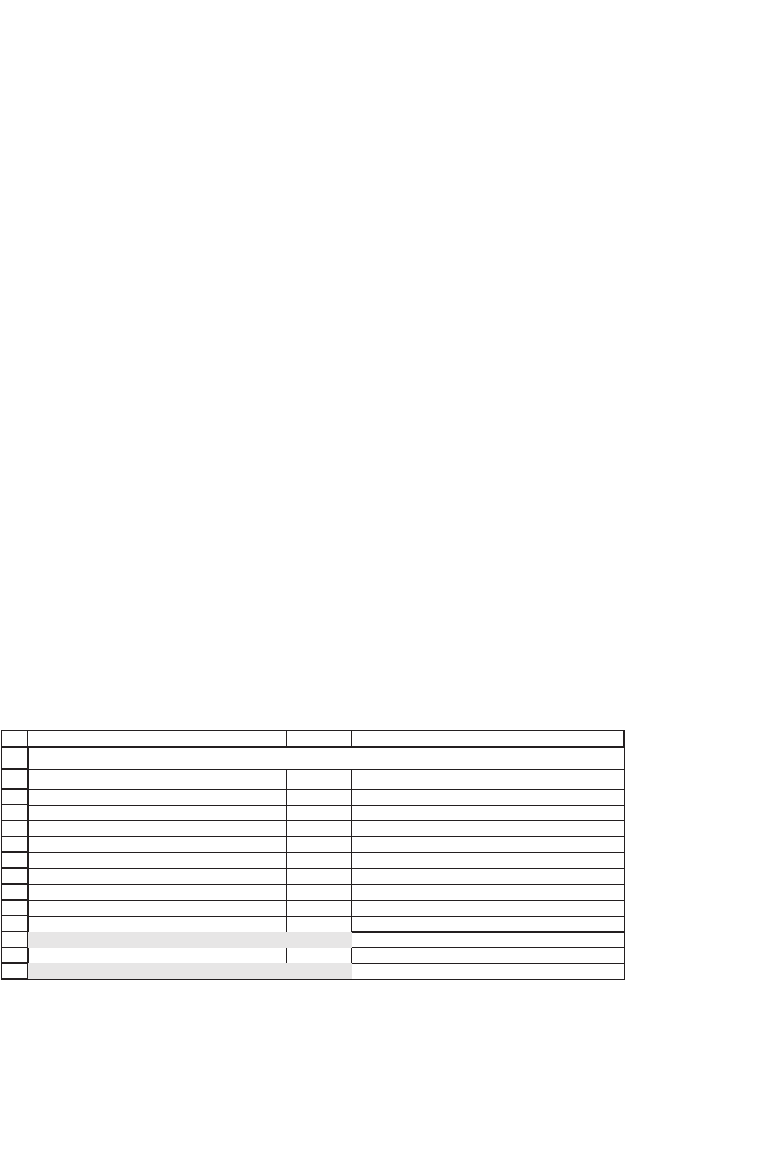
The number of Up moves is stored in a counter called Upcounter, and

the value of the call for each Run is the discounted value of the call

payoff for a particular terminal price S

*Up

Upcounter

Down

Pathlength–Upcounter

where pathlength = Int(Time / deltat) is the integer part of

T/Δt:

pathlength = Int(Time / deltat)

‘Risk-neutral probabilities

piup = (interestdelta - down) / (up - down)

pidown = 1 - piup

Temp = 0

For Index = 1 To Runs

Upcounter = 0

‘Generate terminal price

For j = 1 To pathlength

If Rnd > pidown Then Upcounter = _

Upcounter + 1

Next j

callvalue = Application.Max(S0 * _

(up ^ Upcounter) * _

(down ^ (pathlength - Upcounter)) _

- Exercise, 0) / (interestdelta ^ _

pathlength)

Temp = Temp + callvalue

Next Index

VanillaCall = Temp / Runs

End Function

callvalue = Application.Max(S0 * (up ^ Upcounter) * _

(down ^ (pathlength - Upcounter)) _

- Exercise, 0) / (interestdelta ^ pathlength)

621 Using Monte Carlo Methods for Option Pricing

The Monte Carlo value of the call is given by VanillaCall = Temp

/ Runs.

23.4.2 Understanding the Principles of the Monte Carlo Simulation

For future reference we state the principles of the Monte Carlo simula-

tion. These principles hold not only for the plain-vanilla options of this

section but also for the Asian options treated later in this chapter:

•

Price paths are generated by using the risk-neutral probabilities. In the

program Vanillacall, for example, the price of the stock moves Up if

the random-number generator is greater than π

and moves Down if

the random-number generator is less than or equal to π

. Effectively,

therefore, the risk-neutral probabilities {π

= 1 − π

, π

} of each price

path are incorporated into the price path itself.

•

The value of the option using Monte Carlo is determined by the dis-

counted value of the simple average of all results over the price paths

generated.

23.4.3 Implementing the MC Function VanillaCall in a Spreadsheet

The following spreadsheet shows the implementation of VanillaCall. The

value in cell B14 is the option value as computed by the Black-Scholes

formula; the function BSCall was deﬁ ned in Chapter 19.

CBA

, current stock price

X, exercise price 50

r, interest rate 10%

T, time 0.8

, mean stock return

33%

, sigma--standard deviation of stock return

30%

n, divisions of unit time 200

Runs 3,000

VanillaCall 7.4417 <-- =vanillacall(B2,B3,B6,B7,B4,B5,B9,B10)

BS call 7.2782 <-- =BSCall(B2,B3,B5,B4,B7)

MONTE CARLO PRICING OF PLAIN-VANILLA CALLS

The function divides the time to option expiration T = 0.8 (cell B5)

into 200 divisions (cell B9), so that Δt = 1/200. Each time the function

is called, it runs 3,000 price paths (cell B10). A particular call of this

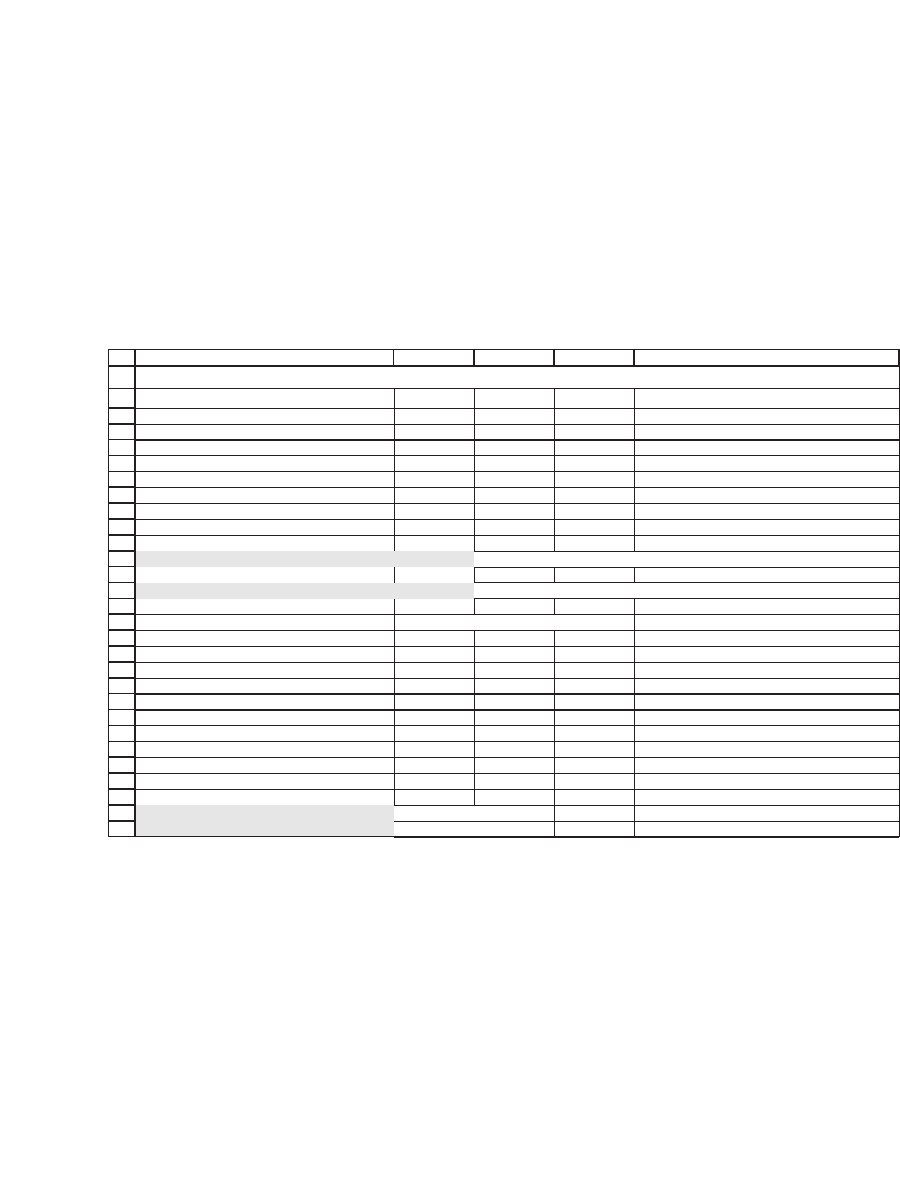
622 Chapter 23

function produced the value 7.4417 (cell B12), whereas the Black-Scholes

call value—computed with the function BSCall deﬁ ned in Chapter 19—

is 7.2782 (cell B14).

How good is this MC routine? One way to test it is to run it many

times. In the next spreadsheet, we’ve run 40 instances of the function

VanillaCall.

BAC ED

, current stock price

X, exercise price 50

r, interest rate 10%

T, time 0.8

, mean stock return

33%

, sigma--standard deviation of stock return

30%

n, divisions 100

Runs 3,000

VanillaCall 7.1404 <-- =vanillacall(B2,B3,B6,B7,B4,B5,B9,B10)

BS call 7.2782 <-- =BSCall(B2,B3,B5,B4,B7)

Multiple runs of the function

7.0727 7.4166 7.4725 6.8758 <-- =vanillacall(B2,B3,B6,B7,B4,B5,B9,B10)

7.2110 7.4123 7.0760 7.4490 <-- =vanillacall(B2,B3,B6,B7,B4,B5,B9,B10)

7.3331 7.5241 7.3272 7.2245 <-- =vanillacall(B2,B3,B6,B7,B4,B5,B9,B10)

7.2895 7.6088 7.4434 7.4520

7.4052 7.2947 7.1995 7.4959

7.0948 7.2209 7.2246 7.3204

7.1768 7.3582 7.4190 7.2144

7.1601 7.1392 7.0774 7.2948

7.0564 7.3033 7.2096 7.2723

7.1043 7.1631 7.6564 7.0906

7.2785 <-- =AVERAGE(A17:D26)

0.1673 <-- =STDEV(A17:D26)

RUNNING THE MONTE CARLO FUNCTION MANY TIMES

The average value (cell B28) has a relatively low standard deviation

(cell B29). The Monte Carlo routine works pretty well.

23.4.4 Improving the Efﬁ ciency of the MC Routine

Monte Carlo routines are inherently very wasteful—you have to run

them many times to get a reasonable approximation to the true value.

Thus there is a lot of mileage in making a particular routine more efﬁ -

cient. Continuing with our VanillaCall example, we show one example

of such an efﬁ ciency gain.

623 Using Monte Carlo Methods for Option Pricing

Function BetterVanillaCall(S0, Exercise, Mean, _

Sigma, Interest, Time, Divisions, Runs)

deltat = Time / Divisions

interestdelta = Exp(Interest * deltat)

up = Exp(Mean * deltat + Sigma * Sqr(deltat))

down = Exp(Mean * deltat - Sigma * Sqr(deltat))

pathlength = Int(Time / deltat)

‘Risk-neutral probabilities

piup = (interestdelta - down) / (up - down)

pidown = 1 - piup

Temp = 0

For Index = 1 To Runs

Upcounter = 0

‘Generate terminal price

For j = 1 To pathlength

If Rnd > pidown Then Upcounter = Upcounter + 1

If S0 * up ^ (Upcounter + n - j) * _

down ^ (j - Upcounter) < X then Goto Compute

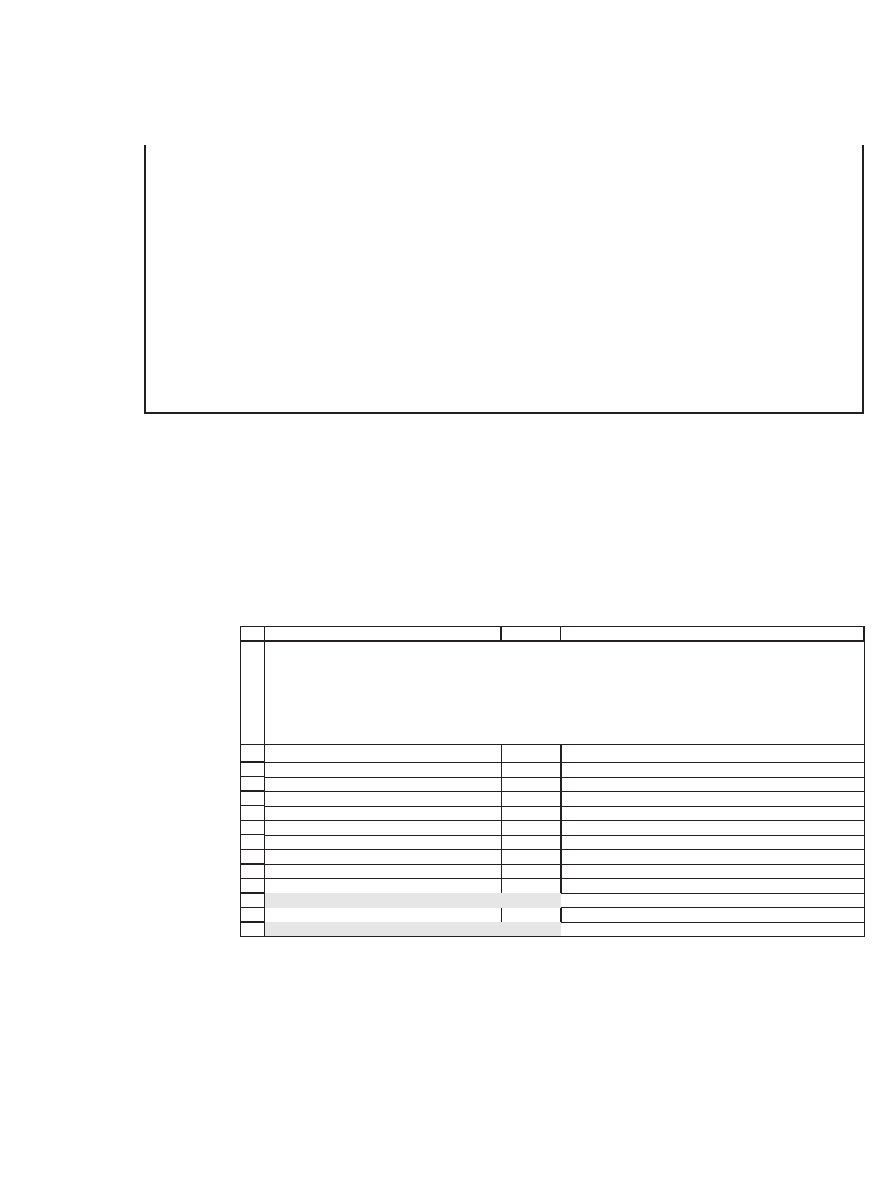
Suppose that after j random numbers the random price is such

that there is no chance that the call option will be in the money.

Denote the number of Ups after j random coin tosses by Upcounter(j).

Then the call option cannot be in the money after n random numbers

if S

Upcounter(j)+(n−j)

Down

j−Upcounter(j)

< X. This formula assumes that all the

remaining random numbers (there will be n − j such numbers) will give

an Up stock-price movement.

For this case, we should stop choosing random numbers after j and let

the call value be zero. The following VBA routine implements this

logic:

624 Chapter 23

Next j

Compute:

callvalue = Application.Max(S0 * (up ^ _

Upcounter) * (down ^ (pathlength - Upcounter)) _

- Exercise, 0) / (interestdelta ^ pathlength)

Temp = Temp + callvalue

Next Index

BetterVanillaCall = Temp / Runs

End Function

The highlighted portions of the code show the changes. The lines called

Compute simply calculate the Callvalue.

The following spreadsheet shows the implementation:

CBA

, current stock price

X, exercise price 45

r, interest rate 6%

T, time 0.8

, mean stock return

12%

, sigma--standard deviation of stock return

30%

n, divisions 100

Runs 2,000

VanillaCall 9.2110 <-- =bettervanillacall(B2,B3,B6,B7,B4,B5,B9,B10)

BS call 9.2931 <-- =BSCall(B2,B3,B5,B4,B7)

MONTE CARLO PRICING OF PLAIN-VANILLA CALLS

BetterVanillaCall: A somewhat more efficient function: If, after j random

numbers that produce

Up moves, S

*Up

(k+n-j)

*Down

(j-k)

<X, then we abort

the random price path and let the call value = 0

625 Using Monte Carlo Methods for Option Pricing

23.4.5 Where Do We Go from Here?

Now that we understand the Monte Carlo technology and its implemen-

tation in VBA, we can extend our examples in two directions. In the next

two sections we discuss the pricing of Asian options—options in which

the option’s terminal payoff depends on the average price over the path.

In section 23.7 we discuss the pricing of barrier options.

23.5 Pricing Asian Options

An Asian option is an option whose payoff depends in some way on the

average price of the asset over a period of time prior to option expira-

tion.

Asian options are sometimes called “average price options.” There

are two common kinds of Asian options:

•

In the ﬁ rst kind of Asian option, the option’s payoff is based on differ-

ence between the average price of the underlying asset and the strike

price: max[Average underlying − Strike, 0]. The examples in Figures 23.3

and 23.4 of the oil contract traded on the NYMEX and the traded

average price option (TAPO) traded on the London Metals Exchange

are this kind of option.

•

In the second kind of Asian option, the option’s exercise price is the

average of the underlying asset’s price over a period preceding option

maturity: max[Terminal underlying − Average underlying, 0]. Such

average strike options are common in markets for electric energy. They

assist hedgers whose primary risks are related to the average price of the

underlying.

Asian options are particularly useful when the user sells the underly-

ing during the period and is therefore exposed to the average price and

when there is danger of price manipulation in the underlying. The Asian

option mitigates the effect of manipulation, since it is based not on a

single price, but on a sequence of prices.

3. See http://www.riskglossary.com/articles/asian_option.htm and http://www.global-

derivatives.com/options/asian-options.php for some deﬁ nitions and a discussion of the

literature. A list of references is also given in the bibliography section of this book.

626 Chapter 23

Figure 23.3

Average price crude oil options traded on NYMEX. http://www.nymex.com/AO_spec.

aspx

627 Using Monte Carlo Methods for Option Pricing

Figure 23.4

Asian options on copper traded on the London Metals Exchange (LME). http://www.

basemetals.com/html/cuinfo.htm

23.5.1 An Initial Example of an Asian Option

We start by considering an Asian option on a stock whose price either

increases by 40 percent or decreases by 20 percent each period. We look

at ﬁ ve dates, starting with date 0: