Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

588 Chapter 21

The ﬁ rst line of the macro Application.SendKeys (“{Enter}”)

was added because each run of the random number generator brings up

the following dialogue box:

The ﬁ rst line of the macro sends an Enter to answer this dialogue box,

so that the macro automatically enters the data into the range.

21.6 Insuring Total Portfolio Returns

So far we have considered only the problem of constructing artiﬁ cial

puts, one per share. A slightly different version of this problem involves

constructing a portfolio of puts and shares that guarantees the total

dollar returns on the total initial investment. A typical story goes like

this:

You have $1,000 to invest, and you want to guarantee that a year from

now you will have at least $1,000z. Here z is some number, generally

between 0 and 1; for example, a z equal to 0.93, would mean that you

want your ﬁ nal wealth to be at least $930.

You want to invest in a stock

whose current price is S

and in a put on the stock with an exercise price

X. You want the number of puts to be equal to the number of shares.

Given X and S

, the put price is P(S

, X). To implement the strategy, you

must therefore buy α shares, where

α=

1000

()SPSX,

Since you have bought α shares and α puts with an exercise price of

X, the minimum dollar return from your portfolio is αX. You want this

3. As we will show in section 21.6.1, it is possible to insure (up to a point) even with

z > 1.

589 Portfolio Insurance

to be equal to 1,000z, and therefore you solve to get α = 1,000z/X. Thus

you can guarantee your minimum return if

SPSX Xz

+=(),/

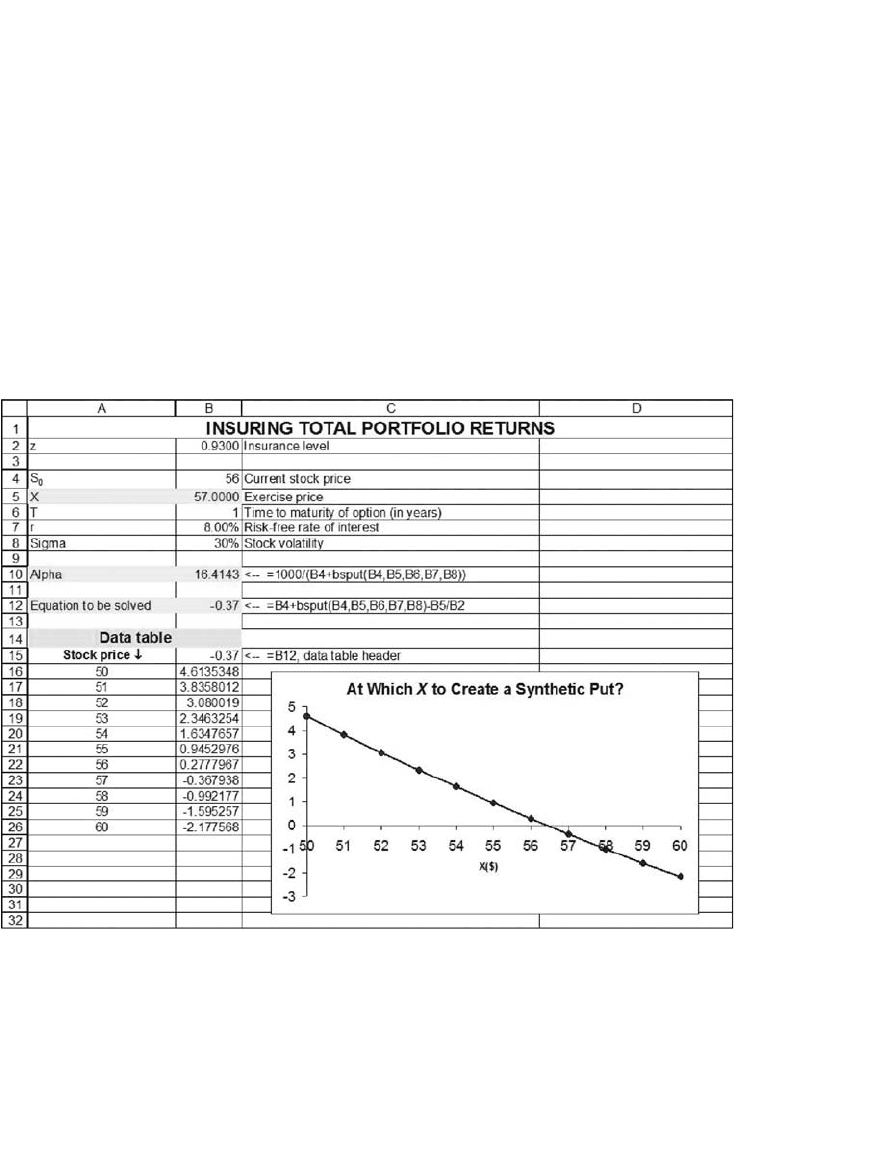
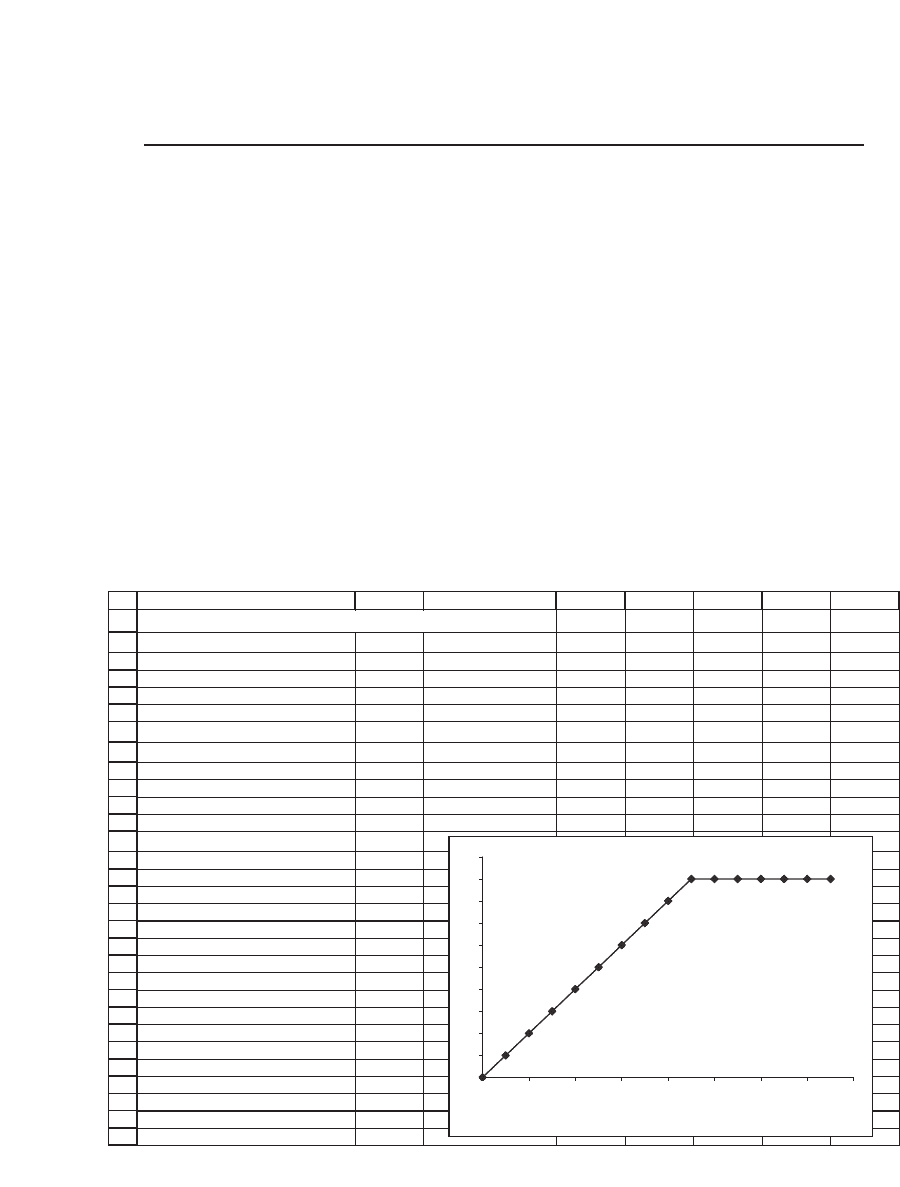
A spreadsheet implementation of this equation follows. The data table

shows the graph of the left-hand side of the preceding equation; where

this graph crosses the x-axis is the solution for the synthetic put exercise

price X when S

= 56, σ = 30 percent, r = 6 percent, T = 1, and z = 93

percent.

Solver gives the solution to the equation S

+ Put(S

, X) − X/z = 0. The

solution is indicated in the next picture:

590 Chapter 21

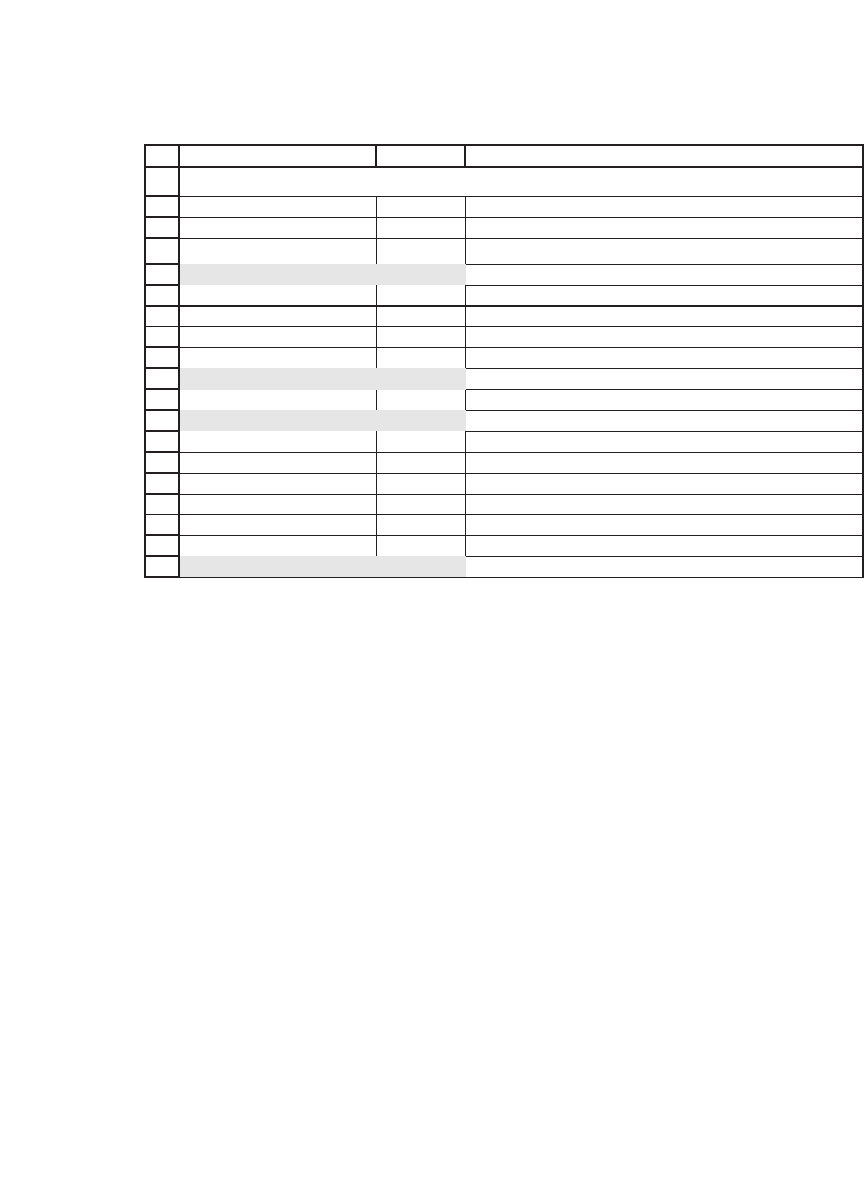
The solution is to buy α = 16.4817 puts and shares (the cost of which

is $1,000, as you can see in cell B17). The minimum return of this port-

folio is 16.4817

X = $930 (cell B19).

21.6.1 What Is the Effect of Raising the Insurance Level? Can You Insure for

More Than Your Initial Investment?

When we raise the insurance level, the implied exercise price of the put

must go up. Therefore, as we buy more insurance, we spend relatively

more of our $1,000 on puts (insurance) and relatively less on the stocks

(which have the upside potential).

Can we insure for more than our current level of investment? To put

it another way, can we set z > 1? We would be picking an insurance level

that guarantees that we end up with more than our initial investment. A

little thought and some calculations reveal that we can indeed choose z

> 1 as long as z ≤ 1 + r. That is, we cannot guarantee ourselves a return

greater than the riskless interest rate! To demonstrate this point, we offer

two examples. In the ﬁ rst example, we solve for z = 1.08 = 1 + r. This has

a solution (note that the value of cell B12 is zero):

AB C

z 0.9300 Insurance level

56 Current stock price

X 56.4261 Exercise price

T 1 Time to maturity of option (in years)

r 8.00% Risk-free rate of interest

Sigma 30% Stock volatility

Alpha 16.4817 <-- =1000/(B4+bsput(B4,B5,B6,B7,B8))

Equation to be solved 0.00 <-- =B4+bsput(B4,B5,B6,B7,B8)-B5/B2

Check

Cost of shares 922.98

Cost of puts 77.02

Total cost 1000.00

Minimum portfolio return 930.00 <-- =B10*B5

INSURING TOTAL PORTFOLIO RETURNS

591 Portfolio Insurance

When z > 1.08, however, there is no solution. Even the best efforts of

Solver do not give zero in cell B12, as you can see in the following

example:

AB C

z 1.0800 Insurance level

56 Current stock price

X 104.8368 Exercise price

T 1 Time to maturity of option (in years)

r 8.00% Risk-free rate of interest

Sigma 30% Stock volatility

Alpha 10.3017 <-- =1000/(B4+bsput(B4,B5,B6,B7,B8))

Equation to be solved 0.00 <-- =B4+bsput(B4,B5,B6,B7,B8)-B5/B2

Check

Cost of shares 576.90

Cost of puts 423.10

Total cost 1,000.00

Minimum portfolio return 1,080.00 <-- =B10*B5

INSURING TOTAL PORTFOLIO RETURNS

AB C

z 1.0900 Insurance level

56 Current stock price

X 122.8824 Exercise price

T 1 Time to maturity of option (in years)

r 8.00% Risk-free rate of interest

Sigma 30% Stock volatility

Alpha 8.8099 <-- =1000/(B4+bsput(B4,B5,B6,B7,B8))

Equation to be solved 0.77 <-- =B4+bsput(B4,B5,B6,B7,B8)-B5/B2

Check

Cost of shares 493.35

Cost of puts 506.65

Total cost 1,000.00

Minimum portfolio return 1,082.58 <-- =B10*B5

INSURING TOTAL PORTFOLIO RETURNS

592 Chapter 21

21.7 Implicit Puts and Asset Values

Up to this point in the chapter, we have been discussing the construction

of puts in order to construct portfolio insurance. We will now reverse the

logic and consider situations in which we are offered a package that

includes an implicit put. The problem is how to deduce the true value of

the underlying asset that is part of the package.

Many commonly encountered situations include implicit puts. Con-

sider the situation in which you are offered an asset plus an option to

have the seller repurchase the asset. Some examples that come to mind

are irrevocable tender offers, “satisfaction guaranteed or your money

back” offers, and computer sales where you get to return the item but

have to pay a 15 percent “restocking charge.” (See Bhagat, Brickley, and

Loewenstein, 1987, for an application of these ideas to cash tender

offers.)

Were you in possession of the asset’s variance, you could deduce from

the offer the true value of the asset. Without this information, you can

deduce the locus of the asset’s standard deviation and its true value. To

do so, let V

denote the true value of the asset stripped of any puts or

repurchase offers. Let V

denote the value of the put. Let Y denote the

purchase price (which, of course, includes the put), and let X denote the

price at which you can get your money back. Then it follows that

YVV

If we assume that the put option can be priced by the Black-Scholes

formula, we will have

VVNdXeNTd

=− − + −

−

() ( )

where

VX rT T

⎛

⎝

⎞

⎠

ln /()

Thus, to solve this problem, we must ﬁ nd a σ and V

that simultaneously

solve

YVNd XeN Td

=+ −

−

() ( )

593 Portfolio Insurance

The right-hand side of this equation is increasing in σ and in V

Here is an example: You are offered a risky asset for $100. If not satis-

ﬁ ed with the asset, you may return it within one year and get back $85

(the remaining $15 is a “restocking charge”). How much is the asset

worth? If you think that the asset’s σ is 30 percent, then we have to

solve

YVNd XeN Td

=+ −

−

() ( )

where Y = 100, σ = 30 percent, T = 1, r = 10 percent, and X = 85.

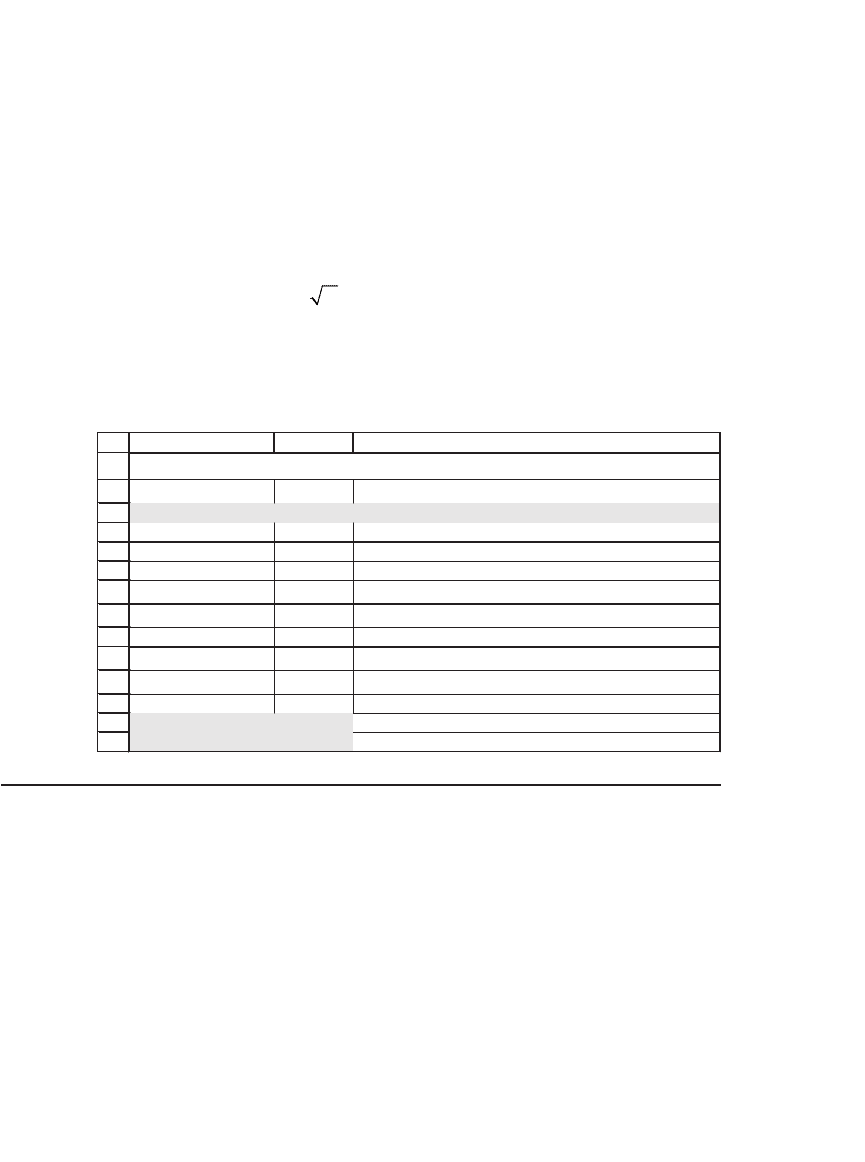
The answer, calculated in the following spreadsheet using Tools|Solver,

is that the underlying asset value V

= $96.71:

AB C

96.70586 Actual asset value

X 85 Money-back guarantee

r 10.00% Risk-free rate of interest

T 1 Time to maturity of option (in years)

Sigma 30% Stock volatility

0.9134 <-- (LN(S/X)+(r+0.5*sigma^2)*T)/(sigma*SQRT(T))

0.6134

<-- d

- sigma*SQRT(T)

N(d

)

0.8195

<-- Uses formula NormSDist(d

)

N(d

)

0.7302

<-- Uses formula NormSDist(d

)

Put price 3.29 <-- =-B3*(1-B11)+B4*EXP(-B5*B6)*(1-B12)

Put + asset value 100.00 <-- =B3+B14

IMPLICIT PUTS AND ASSET VALUES

21.8 Summary

This chapter has concentrated mainly on implementing the classic port-

folio insurance strategies by which we delta hedge a put on a portfolio.

In many ways these strategies are no different from the delta hedging

discussed in Chapter 20, though the implementation to portfolio insur-

ance is important enough to warrant a chapter of its own.

Portfolio insurance strategies simulate a put on the stock, with the

result that the total minimal return is less than what is implied by the

ratio X/S

. What if we want to insure the total portfolio value? This ques-

tion is discussed in section 21.6. A ﬁ nal discussion on this topic is the

implied put value in a money-back guarantee, section 21.7.

594 Chapter 21

Exercises

1. You are a portfolio manager, and you want to invest in an asset having σ = 40

percent. You want to create a put on the investment so that at the end of the year

you have losses no greater than 5 percent. Since there is no put on this speciﬁ c asset,

you plan to create a synthetic put by engaging in a dynamic investment strategy—

purchasing a portfolio composed of dynamically changing proportions of the risky

asset and riskless bonds. If the interest rate is 6 percent, how much should your

initial investment be in the portfolio and in the riskless bond?

2. Simulate the strategy of exercise 1, assuming weekly rebalancing of the portfolio.

3. Go back to the numerical example of section 21.7. Write a VBA function that solves

for the implied asset value V

. (Hint: Use the bisection method.) Then use this func-

tion to create a graph showing the trade-off between the implied asset value and

the asset volatility.

4. You have been offered the chance to purchase stock in a ﬁ rm. The seller wants $55

per share, but offers to repurchase the stock at the end of one-half year for $50 per

share. If the σ of the share’s log returns is 80 percent, determine the true value per

share. Assume that the interest rate is 10 percent.

5. A covered call is a long stock and short call. The pattern of payoffs is as follows:

ABCDEFGH

Future stock price, S

Call exercise price, X 45

6ecirp llaC

Payoffs at T

Long stock, +S

50 <-- =B2

Short call payoff, -Max[S

-X,0]

-5 <-- =-MAX(B2-B3,0)

8B+7B= --<54ffoyap latoT

Data table of payoffs

Future stock price, S

0101

5151

0202

5252

0303

5353

0404

5454

5405

5455

5406

5456

5407

5457

COVERED CALL PROFIT PATTERN

0 1020304050607080

Stock price, S

595 Portfolio Insurance

Simulate the payoffs of a covered call over 52 weeks, with weekly updating of the

positions. Start by deriving the formula for the covered call—add together the

Black-Scholes price and the stock price:

S SNd Xe Nd S

001 20

↑

−

↑

−+ =

Long stock

Short call





() () (−−+

↑

−

↑

Nd Xe Nd

()) ()

Long position

in stock

Long positio



in bond



Thus we see that a covered call is a long position in the stock and a long position

in the bond. Now implement the following spreadsheet to test the effectiveness of

a simulated covered call strategy:

ABCDEFGHIJK

Initial stock price, S

Mean stock return

12%

Sigma

40%

Interest rate, r

Initial call price

11.7393 <-- =bscall(B2,B3,1,B6,B5)

Initial investment in

covered call

38.2607 <-- =B2-B8

Simulated payoff

of strategy

????

Payoff of covered call

strategy

????

Week Time Stock price

Invested

in stock

Invested

in bond

Total

investment

at beginning

of week

Random

Z at end

of week

Stock

price at

end of

week

Investment

at the end of

week

0 0.0000 50.00 0.6134 13.4903 24.7705 38.2607 0.0035 50.1253 38.3232

1 0.0192 50.13 0.6189 13.4330 24.8902 38.3232

2 0.0385

48 0.9231

49 0.9423

50 0.9615

51 0.9808

COVERED CALL SIMULATION

An Introduction to Monte Carlo Methods

22.1 Overview

Monte Carlo (MC) methods are a variety of random simulations used to

determine the values of parameters. In this introductory chapter we use

MC to determine the value of π. In the next chapter we will use MC to

determine the values of various kinds of options that cannot be readily

priced using closed-form formulas. The MC method has its source in

physics, where it is often used to determine model values for which there

is no analytical solution.

The use of MC in ﬁ nance is similar: MC methods

use simulation to price assets whose prices are not readily determined

by analytical means. In short, if there is no formula for computing the

value of an asset, maybe we can determine its value with a simulation.

Clearly the category of options for which there exist no analytical solu-

tions does not include “plain vanilla” European calls and puts, which can

be priced by the Black-Scholes formula. However, many options are

more complicated than these. In Chapter 23 we will illustrate MC methods

for Asian options (where the terminal payoff of the option is path depen-

dent) and American options.

In this chapter we give a laywoman’s introduction to MC pricing.

a precursor you might want to read Chapter 30, which discusses random-

number generators.

22.2 Computing p Using Monte Carlo

All MC methods involve random simulation. We illustrate how to use

Monte Carlo to calculate the value of π, a number with which you are

presumably familiar.

Here’s our method: We know that the area of the unit circle (circle

with radius 1) is π. It follows that the area of a quarter circle is π/4. We

inscribe a quarter circle into a unit square, as seen in the following illus-

tration. We then proceed to “shoot” random points at the unit square.

Each random point has an x component and a y component. We generate

such points by using the Excel function Rand.

1. Two good Web sites with introductions to MC methods are http://www.phy.ornl.gov/

csep/CSEP/MC/NODE1.html and http://www.puc-rio.br/marco.ind/monte-carlo.html.

2. An excellent nonintroductory text is Glasserman (2005).