Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

578 Chapter 21

This protective put or portfolio insurance strategy guarantees that you

will lose no more than $6 on your share of General Pills stock. If the

stock’s price at the end of the year is more than $50, you will simply let

the put expire without exercising it. However, if the stock’s price at the

end of the year is less than $50, you will exercise the put and collect $50.

It is as if you had purchased an insurance policy on the stock with a $6

deductible.

Of course this protection doesn’t come for free: Instead of investing

$56 in your single share of stock, you have invested $58.38. You could

have deposited the additional $2.38 in the bank and earned interest of 8

percent

$2.38 = $0.19 in the course of the year; alternatively, you could

have used the $2.38 to buy more shares.

21.2 Portfolio Insurance on More Complicated Assets

In the example, we have implemented a portfolio insurance strategy by

purchasing a put whose underlying asset exactly corresponds to our

share portfolio. But this technique may not always be possible:

•

It could be that there is no traded put option on the shares we wish to

insure.

•

It could also happen that we want to purchase portfolio insurance on

a more complicated basket of assets, such as a portfolio of shares. Puts

on portfolios do exist (for example, there are traded puts on the S&P

100 and S&P 500 portfolios), but there are no traded puts on most

portfolios.

It is here that the Black-Scholes option-pricing model comes to our

aid. From this formula it follows that a put option on a stock (from here

on, “stock” will be used to refer to a portfolio of stocks as well as a single

stock) is simply a portfolio consisting of a short position in the stock and

a long position in the risk-free asset, with both positions being adjusted

continuously. For example, consider the Black-Scholes formula for a put

with expiration date T = 1 and exercise price X. At time t, 0 ≤ t < 1, the

put has value

P SNd Xe Nd

=− − + −

−−

() ()

()

where

579 Portfolio Insurance

dd t

(

)

++ −

−

=− −

ln /2)(

()

where 1 − t is time remaining to maturity and S

is the price of the stock

at time t.

Thus buying a put is equivalent to investing Xe

−r(1−t)

N(−d

) in a risk-

free bond that matures at time 1 and investing −S

N(−d

) in the stock.

Since the investment in the stock is negative, a put is equivalent to a

short position in the stock and a long position in the risk-free asset.

The total investment required to buy one share of the stock plus a put

on the stock is S

+ P

. Writing this out and substituting in the Black-

Scholes put formula gives

Total investment, protective put =+

=− − +

−−

SSNd Xe N

()

(()

[()] ()

() (

()

−

=−−+ −

=+ −

−−

SNdXe Nd

SN d Xe N d

))

where the last equality uses the fact that for the standard normal distri-

bution N(x) + N(−x) = 1. An even more useful way of looking at this

problem is to regard the total investment S

+ P

at time t as a portfolio

of a stock and a bond; we can then ask what is the proportion ω

of this

portfolio invested in the stock at time t. Rewriting the preceding formula

in terms of portfolio proportions gives

Proportion invested in stock =

+−

−−

SN d

SN d Xe N d

()

() (

()

))

Proportion invested in risk-free asset =−

−

−−

Xe N d

()

(() ( )

()

dXe Nd

+−

−−

In summary, if you want to buy a speciﬁ c portfolio of assets and an

insurance policy guaranteeing that at t = 1 your total investment will not

be worth less than X, then at each point in time, t, you should invest a

proportion ω

of your wealth in the speciﬁ c portfolio you have chosen,

and a proportion 1 − ω

in riskless, pure-discount bonds that mature at

580 Chapter 21

t = 1. The Black-Scholes put-pricing formula can be used to determine

these proportions.

21.3 An Example

Suppose you decide to invest $1,000 in General Pills (GP) stock (cur-

rently selling at $56) and in protective puts on the shares with an exercise

price of $50 and an expiration date one year from now. This method

insures that your dollar value per share at the end of one year will be no

less than $50. Suppose that there is no traded put on GP, so that you will

have to create your own put by investing in the share and in riskless

discount bonds. The riskless rate of interest is 8 percent, and the standard

deviation of GP’s log return is 30 percent. We will construct a series of

portfolios that implements this strategy on a week-by-week basis.

21.3.1 Week 0

At the beginning of week 0, the initial investment in shares of GP

should be

∗

SNd

56 0 7865

56 2 38

75 45

() .

.percent

with the remaining proportion, 1 − ω

= 24.55 percent, invested in riskless

discount bonds maturing in one year. If traded European puts on GP

existed and if these puts had an exercise price of 50 with an exercise date

one year from now, these would be trading at $2.38. Your strategy would

consist of buying 17.13 shares of GP (cost = $959.23) and 17.13 puts (cost

= $40.77). Buying $754.40 of shares and $245.60 of bonds exactly dupli-

cates the initial investment in 17.13 shares and 17.13 puts. This equiva-

lence is guaranteed by Black and Scholes. The calculations of the option

price and the appropriate portfolio proportions are shown in the follow-

ing spreadsheet picture:

1. There’s an implicit contradiction here between the ﬁ nite updating strategy and the

continuous rebalancing that underlies the Black-Scholes model. This is discussed at the

end of this section.

581 Portfolio Insurance

We now turn to the end of week 0. You started at t = 0 with an initial

investment of $1,000; now suppose that by the end of the ﬁ rst week the

price of GP shares had increased to $60. Then your portfolio value at the

beginning and end of the ﬁ rst week would look like this:

AB C

S56Stock price

X 50 Exercise price

T 1 Time remaining

r 8.00% Risk-free rate of interest

Sigma 30% Stock volatility

0.7944 <-- (LN(S/X)+(r+0.5*sigma^2)*T)/(sigma*SQRT(T))

0.4944

<-- d

-Sigma*SQRT(T)

N(d

)

0.7865

<-- Uses formula NormSDist(d

)

N(d

)

0.6895

<-- Uses formula NormSDist(d

)

Call price 12.22

<-- S*N(d

)-X*exp(-r*T)*N(d

)

Put price 2.38 <-- call price - S + X*Exp(-r*T): by Put-Call parity

Calculating the portfolio insurance proportions

Omega 75.45% <-- =B2*B11/(B2+B15), proportion in shares

1-omega 24.55% <-- =1-B18, proportion in bonds

Black-Scholes Option-Pricing Formula

Applied to General Pills Put

Portfolio value, beginning of week Portfolio value, end of week

Week

Stock price

at begin. of

week

Stock price

at end of

week

beginning

of week

Omega,

beginning

of week

Stocks Bonds

Portfolio

value

Stocks Bonds

Portfolio

value

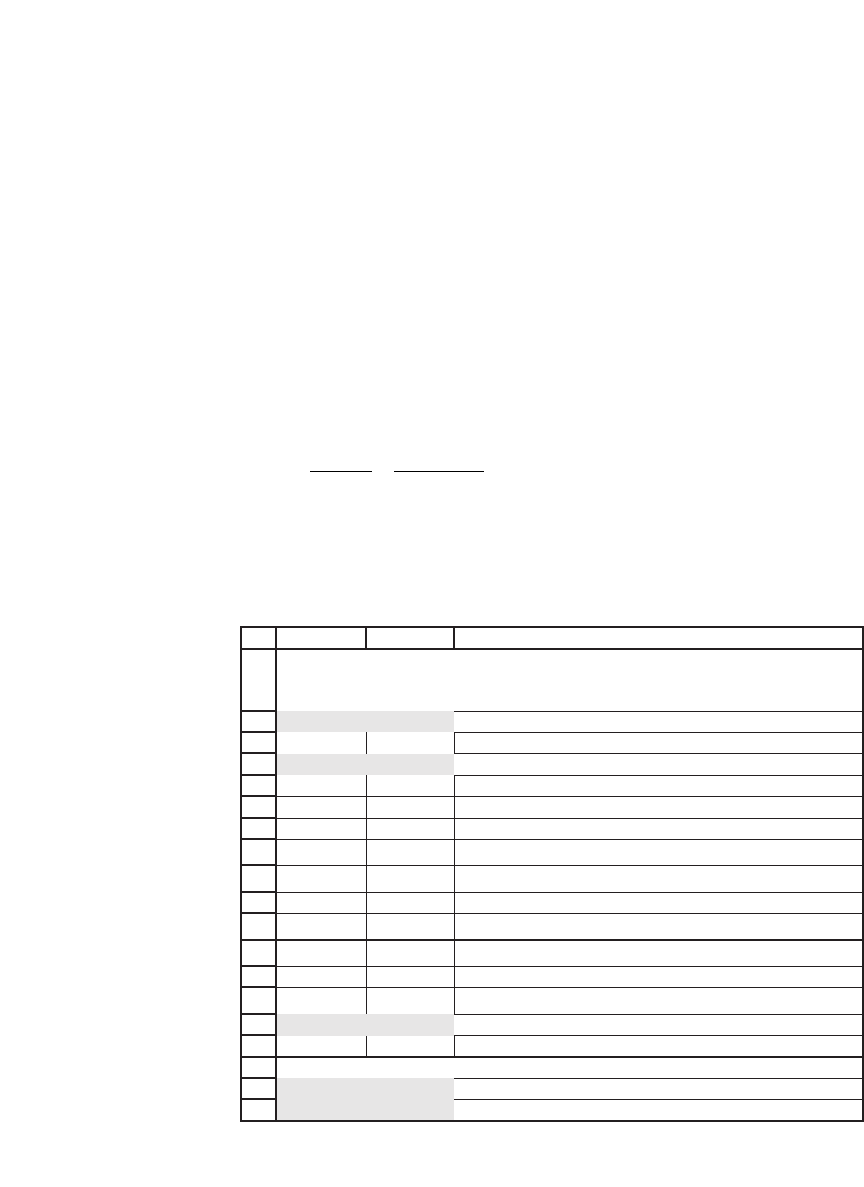
0 56.00 60.00 0.7944 0.7545 754.50 245.50 1000.00 808.39 245.88 1054.27

Note that the value of your bonds at the end of the week is known in

advance; this value grows by a factor of 1.00154 = e

(1/52)0.08

per week.

The

2. Throughout we assume that the interest rate does not change. As an approximation to

reality, this assumption is acceptable in this situation (meaning that the effect of interest

rate changes is much smaller than the effect of changes in the stock price). If we wished

to account for interest-rate changes, then this would add another source of uncertainty

to the model.

582 Chapter 21

value of your shares, however, depends on the rate of growth in the price

of GP stock. During week 0, this rate of growth was 60/56 = 1.0714.

21.3.2 Week 1

At the beginning of week 1 you rebalance your portfolio, increasing the

proportion of equity and decreasing the amount invested in the bonds.

The new portfolio proportions reﬂ ect the time to maturity (time after

one week is t = 1/52 = 0.0192), the stock price at the beginning of the

week ($60), and the total portfolio value at the beginning of the week

($1,054.27). As the next spreadsheet picture shows, you should now

rebalance your portfolio, investing

0.0192

∗

SN d

() .

60 0 8476

60 1 63

82 53 percent

in shares of GP and the remainder, 17.47 percent in bonds. Here $1.63

is the Black-Scholes cost of a European put, calculated with the correct

parameters:

AB C

S60Stock price

X 50 Exercise price

T 0.9808 <-- =1-1/52 , time remaining

r 8.00% Risk-free rate of interest

Sigma 30% Stock volatility

1.0263 <-- (LN(S/X)+(r+0.5*sigma^2)*T)/(sigma*SQRT(T))

0.7292

<-- d

-Sigma*SQRT(T)

N(d

)

0.8476

<-- Uses formula NormSDist(d

)

N(d

)

0.7671

<-- Uses formula NormSDist(d

)

Call price 15.40

<-- S*N(d

)-X*exp(-r*T)*N(d

)

Put price 1.63 <-- call price - S + X*Exp(-r*T): by Put-Call parity

Calculating the portfolio insurance proportions

Omega 82.53% <-- =B2*B11/(B2+B15), proportion in shares

1-omega 17.47% <-- =1-B18, proportion in bonds

Black-Scholes Option-Pricing Formula

Applied to General Pills Put

583 Portfolio Insurance

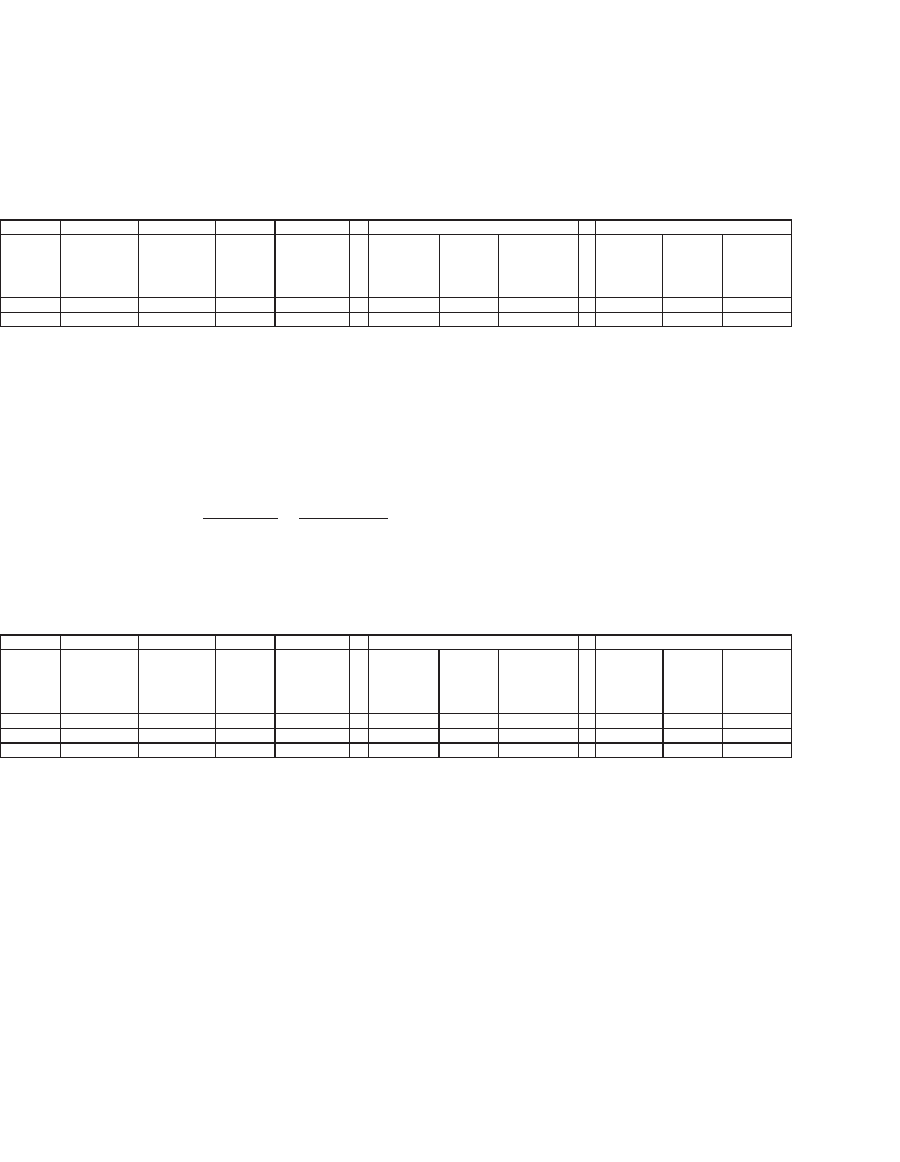
Suppose that at the end of week 1, the price of a share of GP tumbled

to 52. Your position now would look like this:

Portfolio value, beginning of week Portfolio value, end of week

Week

Stock price

at begin. of

week

Stock price

at end of

week

beginning

of week

Omega,

beginning

of week

Stocks Bonds

Portfolio

value

Stocks Bonds

Portfolio

value

0 56.00 60.00 0.7944 0.7545 754.50 245.50 1000.00 808.39 245.88 1054.27

1 60.00 52.00 1.0263 0.8253 870.06 184.22 1054.27 754.05 184.50 938.55

2 52.00 ??? 0.5419 0.6635 622.73 315.82 938.55 ??? 316.30 ???

21.3.3 Week 2

Since another week has passed, the proportion of your investment in GP

should now be

0.0385

∗

SNd

() .

52 0 7061

52 3 33

66 35 percent

This gives

Portfolio value, beginning of week Portfolio value, end of week

Week

Stock price

at begin. of

week

Stock price

at end of

week

beginning

of week

Omega,

beginning

of week

Stocks Bonds

Portfolio

value

Stocks Bonds

Portfolio

value

0 56.00 60.00 0.7944 0.7545 754.50 245.50 1000.00 808.39 245.88 1054.27

1 60.00 52.00 1.0263 0.8253 870.06 184.22 1054.27 754.05 184.50 938.55

The uncertainty will be resolved only when we know the value of the

shares at the end of the week.

Of course this example is somewhat misleading because the Black-

Scholes model assumes that portfolio proportions are continuously

adjusted, whereas we have waited a whole week to readjust our pro-

portions. In the background lurks a pious hope that ﬁ nite (but short)

adjustment intervals will approximate the Black-Scholes continuous-

readjustment scheme. (Since we are only human, we can’t in fact make

continuous adjustments to our portfolio. Moreover, since readjustment

of the portfolio involves transaction costs to the investor, only ﬁ nite

adjustment is possible.)

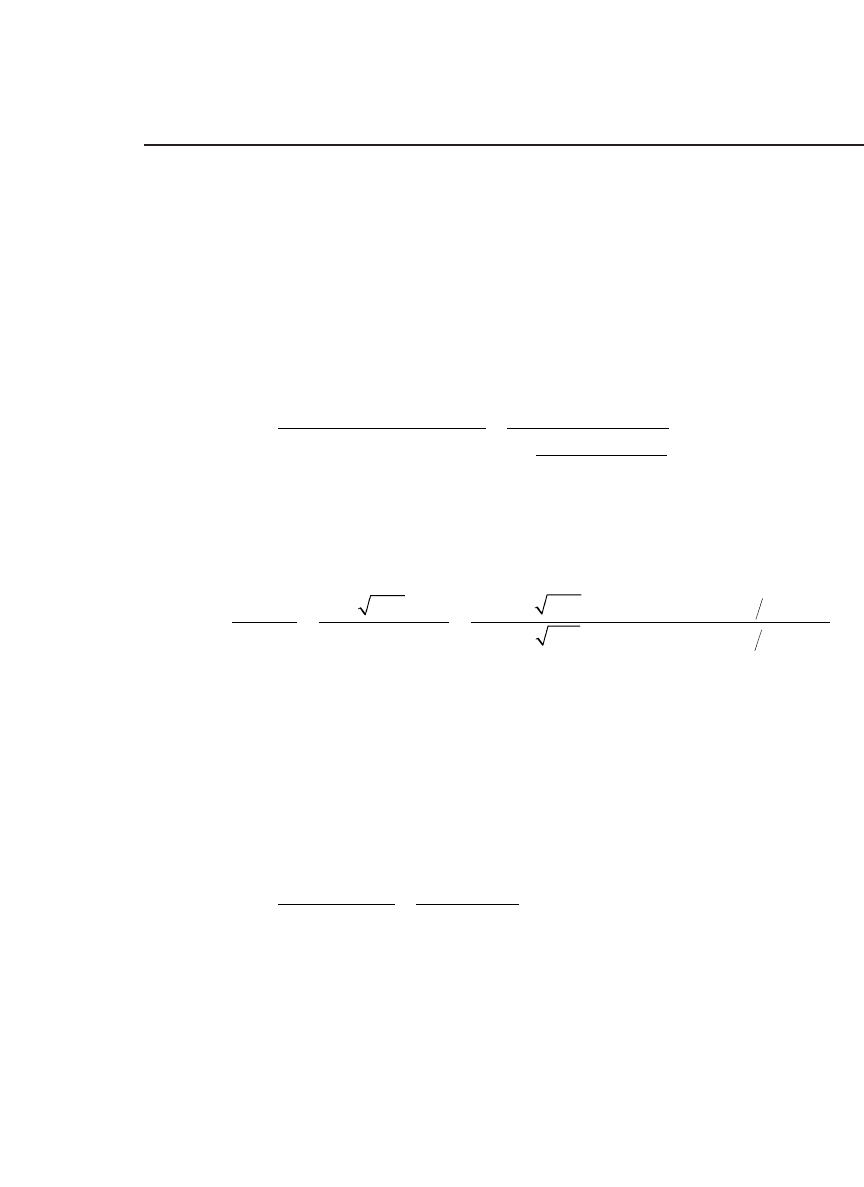
584 Chapter 21

21.4 Some Properties of Portfolio Insurance

The preceding example illustrates some of the typical properties of port-

folio insurance. Three important properties are the following:

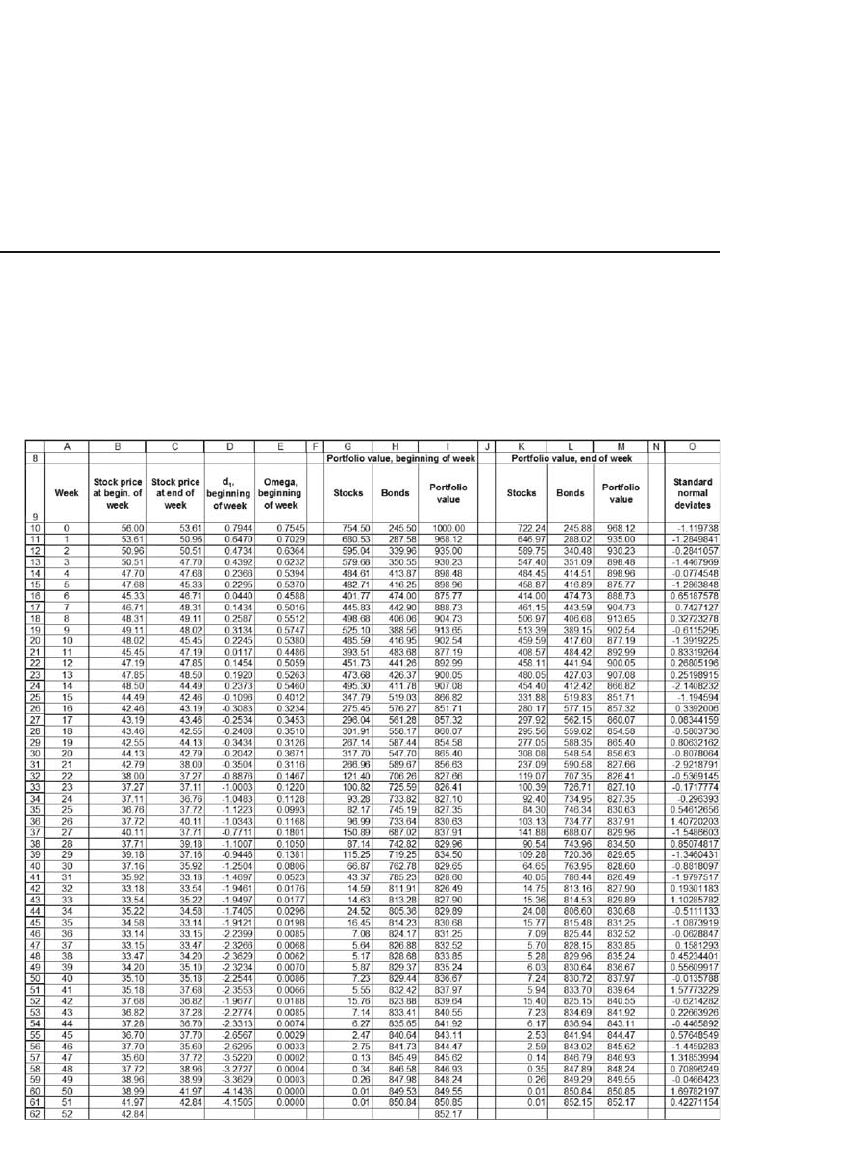
property

1 When the stock price is above the exercise price X, then the

proportion ω invested in the risky asset is greater than 50 percent.

Proof The proof of this property requires a little manipulation of our

formula for ω. Rewrite ω as

ω=

SN d

SN d Xe N d

Xe N d

SN d

()

() ( )

()

+−

−

−−

We will show that when S ≥ X, the denominator of ω is < 2, which will

prove the proposition: First note that when S ≥ X, X/S ≤ 1. Next note

that e

−r(1−t)

< 1 for all 0 ≤ t ≤ 1. Finally, examine the expression

Ntd

NtSXrt

()

(. ( ) ( )

−

−−

−− + −

[]

05 1 1

σσ(1−ln /

NtSXrtt

))

(. ( ) ( ) ))05 1

σ1− σ(1−++−

[]

ln /

This proves the property.

property 2 When the stock’s price increases, the proportion ω invested

in the stock increases and vice versa.

Proof To see this property, it is enough to see that when S increases,

the value of the put decreases and N(−d

) decreases. Rewrite the original

deﬁ nition of ω as

ω=

−−

()

[]

−−

[]

SNd

()

Thus, when S increases, the denominator of ω decreases and the numera-

tor increases, which proves Property 2.

property 3 As t → 1, one of two things happens: If S

> X, then ω

→ 1.

If S

< X, then ω

→ 0.

Proof To see this property, note that when S

> X and t → 1, N(d

) →

1 and N(−d

) → 0; thus for this case ω

→ 1. Conversely, when S

< X and

585 Portfolio Insurance

t → 1, N(d

) → 0 and N(−d

) → 1 and thus ω

→ 0. (Strictly speaking

these statements are only true as “probability limits”—see Billingsley,

1968. What about the case when, as t → 1, S

/X → 1? In this case ω

→

. However, the probability of this occurring is zero.)

21.5 What Do Portfolio Insurance Strategies Look Like? A Simulation

What do portfolio insurance strategies look like? In this section we con-

sider this question by simulating such a strategy. Throughout we assume

that the interest rate is constant and that the stock price is lognormally

distributed. Here is a sample from the output of a simulation:

586 Chapter 21

All the columns of the simulation have already been explained except

column O: This column contains a series of random numbers drawn from

a standard normal distribution. The price of the stock at the end of each

week is determined by these random numbers. In this example the stock

price of 56.87 at the end of week 0 is—as explained in Chapter 18—deter-

mined by the lognormal assumption

SS e

tZt

=∗

−

μσ

ΔΔ

which for this

particular case becomes

56 59 50

015

0 30 0 183745

...

=∗

∗+ ∗

. As explained in

Chapter 18, these standard normal deviates were created with the Excel

command Tools|Data Analysis|Random Number Generation.

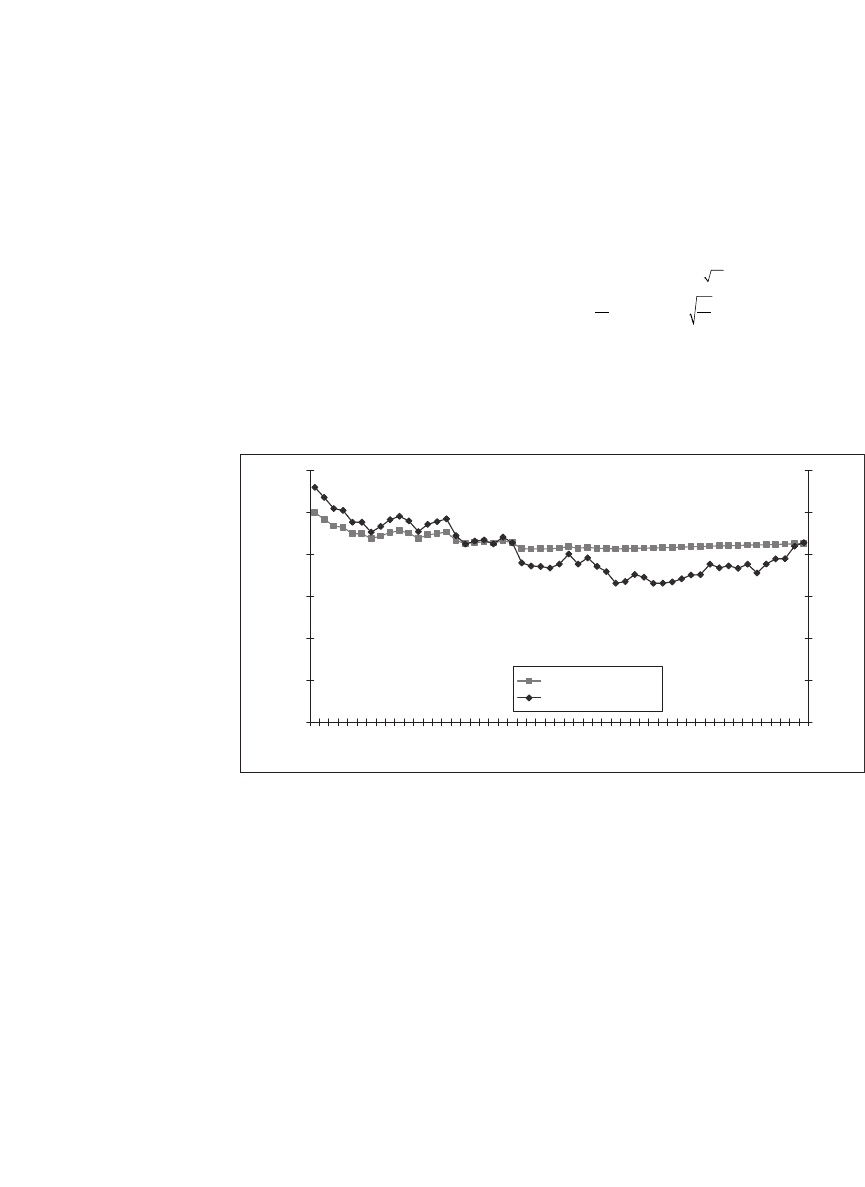
When graphed, the results look like this:

Portfolio Insurance Simulation

200

400

600

800

1,000

1,200

0 2 4 6 8 10121416182022242628303234363840424446485052

Week

Insured portfolio value

Stock price

Insured portfolio

Stock price

In this particular graph the stock price (graphed on the right axis)

declined over the year, so that the portfolio insurance strategy pays off

more than a straight stock strategy would have. In effect, we have used

the puts that are implicit in this strategy.

In this example, the stock price declines below $50 per share. As we

pointed out in section 21.3, at date 0 the portfolio insurance strategy

involved the equivalent of purchasing 17.13 shares of the stock and a put

on each of these shares. If our simulation were continuously updated, the

portfolio value would never dip below $856.50 (= 17.13 * $50). In this

case, because the updating of the portfolio positions is weekly and not

continuous, the terminal value of the portfolio is close to $856. As sug-

gested by Property 3 of section 21.4, by the end of the year, the portfolio

587 Portfolio Insurance

insurance strategy is wholly invested in bonds. By week 47 there is no

investment in stocks whatsoever.

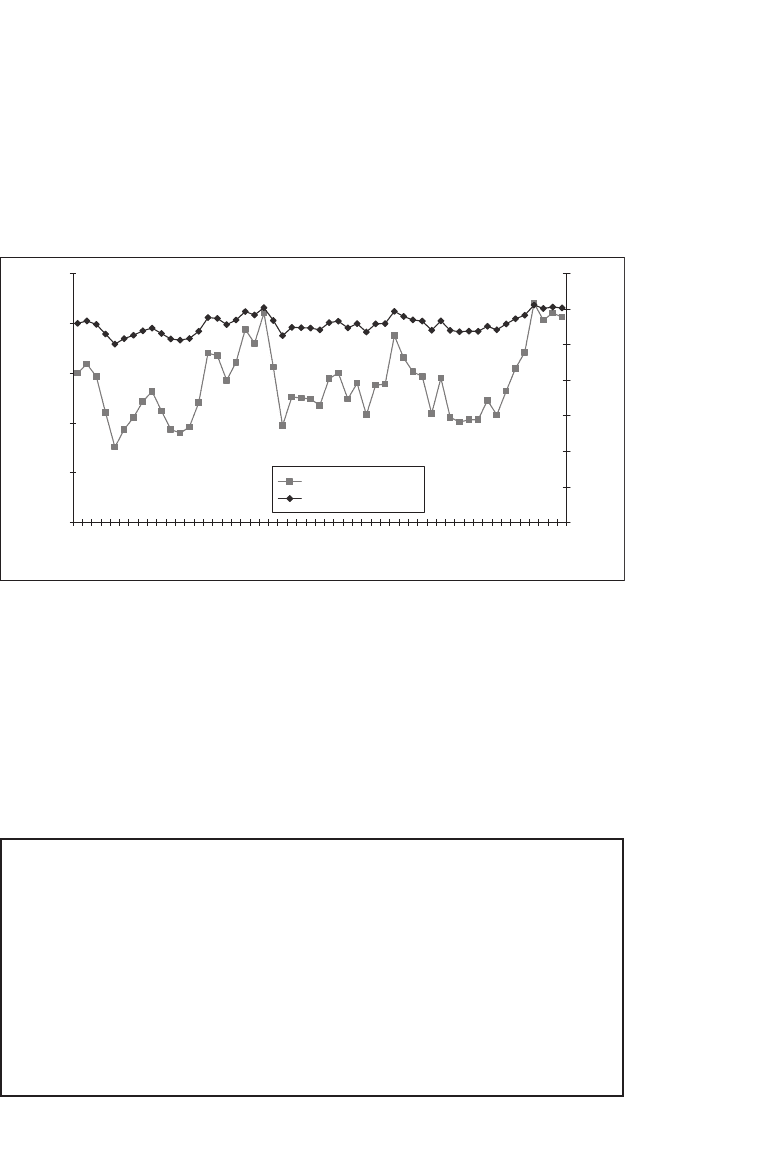
We can rerun the simulation and graph the output, tracking both the

stock price and the total portfolio value over the course of the year:

Portfolio Insurance Simulation

850

900

950

1,000

1,050

1,100

0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52

Week

Insured portfolio value

Stock price

Insured portfolio

Stock price

In this example, by the end of the year the portfolio insurance strategy

will be wholly invested in stocks (again this result follows from Property

3 of section 21.4). In this example the portfolio insurance proves more

expensive than an uninsured investment—ex post, we would have been

better off not following an insurance policy.

We can use the Tools|Record Macro feature of Excel to produce a

macro that automates the simulation procedure.

Sub Simulation()

‘ Simulation Macro

‘ key assigned: [Ctrl]+a

‘

Application.SendKeys (“{Enter}”)

Application.Run “ATPVBAEN.XLA!Random”, _

ActiveSheet.Range(“$O$11:$O$61”), , _

, 2, , 0, 1

End Sub