Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

Option Greeks

20.1 Overview

In this chapter we discuss the sensitivities of the Black-Scholes formula

to its various parameters. The “Greeks,” as they are called (because of

the Greek letters used to denote most of them), are the partial deriva-

tives of the Black-Scholes formula with respect to its arguments. They

can be thought of as giving a measure of the riskiness of an option:

•

Delta, denoted by Δ, is the partial derivative of the option price with

respect to the price of the underlying stock:

ΔΔ

Call Put

∂

∂SS

Delta can be thought of as a measure of the variability of the option’s

price when the price of the underlying stock changes.

•

Gamma, Γ, is the second derivative of the option’s price with respect

to the underlying stock. Gamma gives the convexity of the option price

with respect to the stock price. For options priced by the Black-Scholes

formula, the call and put have the same gamma:

ΓΓ

Call Put

∂

•

Vega is the sensitivity of the option price to the standard deviation of

the underlying stock’s return σ. For no obvious reason, the Greek letter

kappa, κ, is sometimes used to denote vega. Given the Black-Scholes

formula, calls and puts have the same vega:

σσ

∂

Call Put

•

Theta, θ, is change in the option’s value as the time to maturity decreases.

We generally expect that options will become less valuable with

the passage of time (though this assumption turns out not to be always

true). Writing T as the option’s remaining time to maturity, we set theta

equal to the negative of the derivative of the option price with respect

to T:

1. Table 20.1, page 551, gives the formulas for all the Greeks.

550 Chapter 20

θθ

Call Put

=−

∂

=−

∂

∂TT

•

Rho, ρ, measures the interest rate sensitivity of an option:

ρρ

Call Put

=−

∂

=−

∂

∂rr

In this chapter we show you how to measure an option’s Greeks and

how to use them in hedging. For generality we illustrate using the Merton

model (section 19.6.2), an extended version of the Black-Scholes formula

that applies either to stocks paying a continuous dividend or to

currencies.

20.2 Deﬁ ning and Computing the Greeks

The “Greeks” are the sensitivities of an option price with respect to

certain of its variables. In Table 20.1 we set out the Greeks for options

deﬁ ned on an underlying stock that pays a continuous dividend. As dis-

cussed in section 19.6.2, such options are priced using the Merton model.

Of course, the standard Black-Scholes model is obtained from the Merton

model by setting the dividend yield k = 0. Currency options can be priced

by the Merton formula by setting S equal to the current exchange rate,

X equal to the option exercise exchange rate, r equal to the domestic

interest rate, and k equal to the foreign interest rate.

The Merton version of the Black-Scholes formula is given by

CSe Nd XeNd

kT rT

=−

−−

() ()

PSeNdXeNd

kT rT

=− − + −

−−

() ()

where

rk T

⎛

⎝

⎜

⎞

⎠

⎟

+−+ln ( )σ

dd T

=−σ

Table 20.1 gives the Greeks for this formula.

551 Option Greeks

Table 20.1

Black-Scholes Greeks

Measures Call Put

Delta, written as

either Δ or δ

Price sensitivity of

option

∂

Call

= e

−kT

N(d

) Δ

Put

= e

−kT

[N(d

) − 1] =

−e

−kT

N(−d

)

Gamma, written as Γ

Second-order price

sensitivity

∂

. The

option’s convexity

with respect to

underlying price.

eNd

kT d kT−−

′

()

2σσ

Vega, no Greek

letter, though

sometimes the

Greek kappa κ is

used

Sensitivity to

volatility

∂

Se N d T

STe

dkT

−

′

()

Theta, written as θ

Time sensitivity

−

∂

−

′

−

Se N d

kSe N d

rXe N d

()

−

′

−−

+−

−

Se N d

kSe N d

rXe N d

()

Rho, ρ

Interest rate

sensitivity

XTe

−rT

N(d

) −XTe

−rT

N(−d

)

Reminders:

dd T

−+

()

=−

ln( )

′

−

()

Nx e

()

VBA Implementation of Black-Scholes Greeks

Function dOne(stock, exercise, time, interest, _

divyield, sigma)

dOne = (Log (stock / exercise) + _

(interest - divyield) _

* time) / (sigma * Sqr(time)) + 0.5 * _

sigma * Sqr(time)

End Function

Function dTwo(stock, exercise, time, interest, _

divyield, sigma)

552 Chapter 20

dTwo = dOne(stock, exercise, time, _

interest, divyield, sigma) - sigma _

* Sqr(time)

End Function

‘The standard normal probability density, this is

‘N′ (x)

Function normaldf(x)

normaldf = Exp(-x ^ 2 / 2) / _

(Sqr(2 * Application.Pi()))

End Function

Function BSMertonCall(stock, exercise, time, _

interest, divyield, sigma)

BSMertonCall = stock * Exp(-divyield * time) * _

Application.NormSDist(dOne(stock, exercise, _

time, interest, divyield, sigma)) - exercise * _

Exp(-time * interest) * Application.NormSDist _

(dTwo (stock, exercise, time, interest, _

divyield, sigma))

End Function

'Put pricing function uses put-call parity theorem

Function BSMertonPut(stock, exercise, time, _

interest, divyield, sigma)

BSMertonPut = BSMertonCall(stock, exercise, _

time, interest, divyield, sigma) + exercise * _

Exp(-interest * time) - stock * Exp(-divyield _

* time)

End Function

Function DeltaCall(stock, exercise, time, interest, _

divyield, sigma)

DeltaCall = Exp(-divyield * time) * _

Application.NormSDist(dOne(stock, exercise, _

time, interest, divyield, sigma))

End Function

553 Option Greeks

Function DeltaPut(stock, exercise, time, interest, _

divyield, sigma)

DeltaPut = -Exp(-divyield * time) * _

Application.NormSDist (-dOne(stock, exercise, _

time, interest, divyield, sigma))

End Function

Function Gamma(stock, exercise, time, interest, _

divyield, sigma)

Gamma = (Exp(dOne(stock, exercise, time, _

interest, divyield, sigma) ^ 2 / 2 - _

divyield * time)) / (stock * sigma * _

Sqr(2 * time * Application.Pi()))

End Function

Function Vega(stock, exercise, time, interest, _

divyield, sigma)

Vega = stock * Sqr(time) * normaldf(dOne(stock, _

* Exp(-divyield * time)

End Function

Function ThetaCall(stock, exercise, time, interest, _

divyield, sigma)

ThetaCall = -stock * normaldf(dOne(stock, _

exercise, time, interest, divyield, sigma)) * _

sigma * Exp(-divyield * time) / _

(2 * Sqr(time)) + divyield * stock * _

Application.NormSDist(dOne(stock, exercise, _

time, interest, divyield, sigma)) * _

Exp(-divyield * time) _

- interest * exercise * Exp(-interest * time) _

* Application.NormSDist(dTwo(stock, exercise, _

time, interest, divyield, sigma))

End Function

554 Chapter 20

Function ThetaPut(stock, exercise, time, interest, _

divyield, sigma)

ThetaPut = -stock * normaldf(dOne(stock, _

exercise, time, interest, divyield, sigma)) _

* sigma * Exp(-divyield * time) / _

(2 * Sqr(time)) - divyield * _

stock * Application.NormSDist(-dOne(stock,

exercise, time, interest, divyield, _

sigma)) * Exp(-divyield * time) + interest _

* exercise * Exp(-interest * time) * _

Application.NormSDist (-dTwo(stock, exercise, _

time, interest, divyield, sigma))

End Function

Function RhoCall(stock, exercise, time, interest, _

divyield, sigma)

RhoCall = exercise * time * Exp(-interest * _

time) * Application.NormSDist(dTwo(stock, _

exercise, time, interest, divyield, sigma))

End Function

Function RhoPut(stock, exercise, time, interest, _

divyield, sigma)

RhoPut = -exercise * time * Exp(-interest * _

time) * Application.NormSDist(-dTwo(stock, _

exercise, time, interest, divyield, sigma))

End Function

The Greeks are implemented in the following spreadsheet, which

shows both the brute-force calculation of each Greek and a VBA func-

tion implementation.

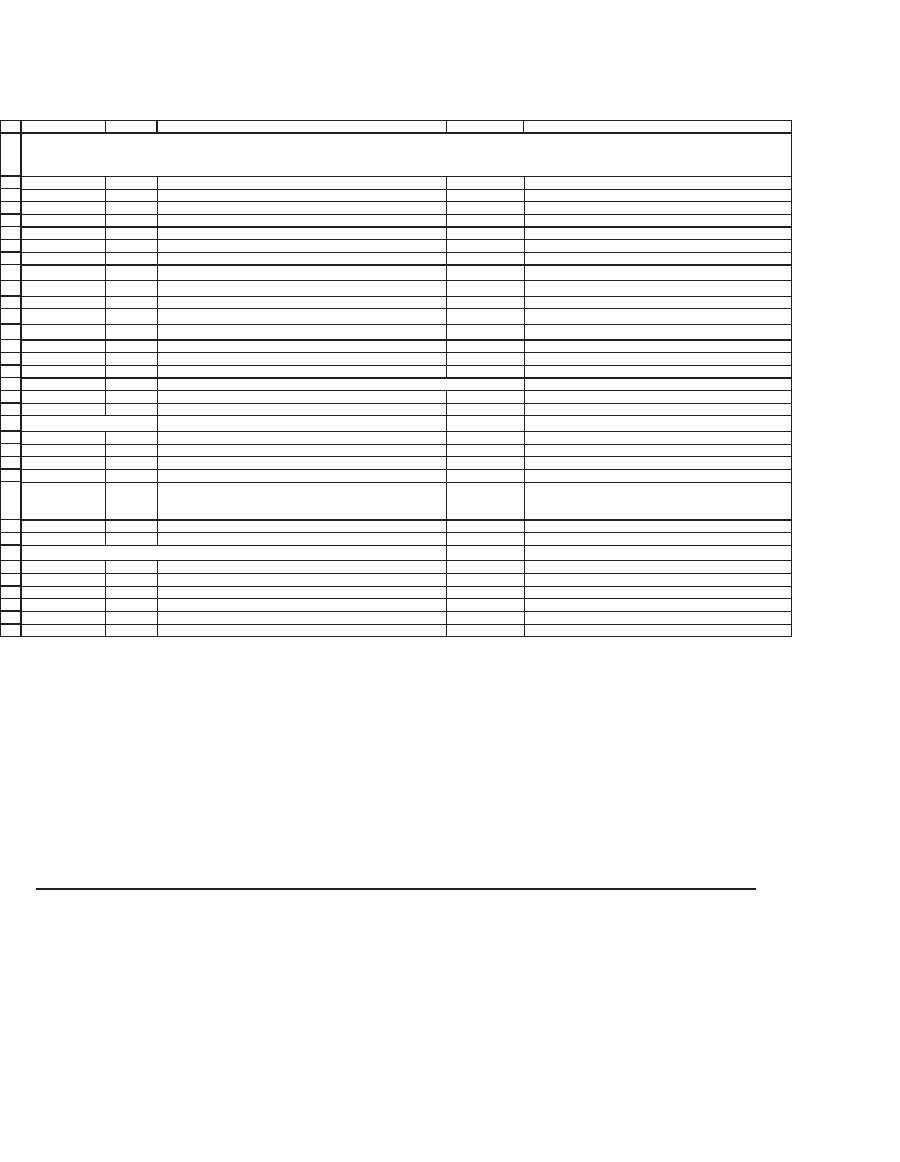
555 Option Greeks

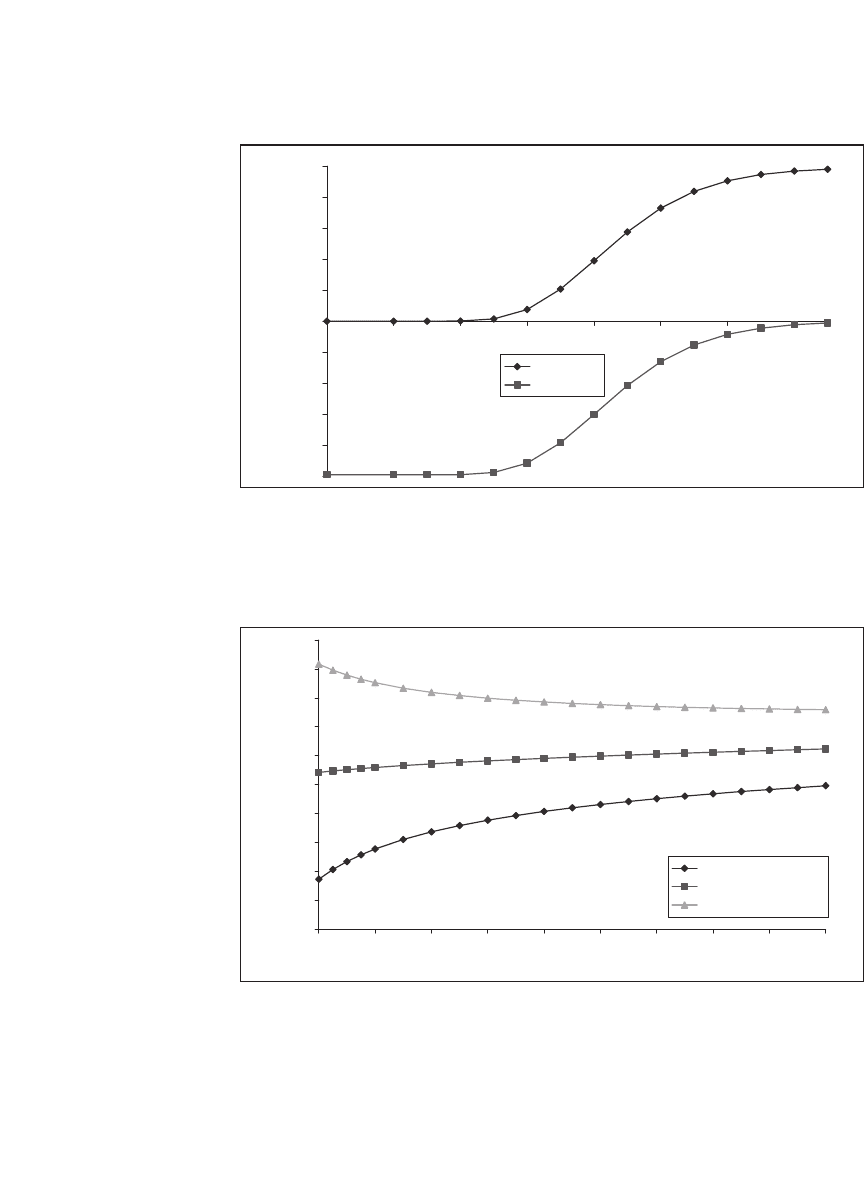
Excel can be used to examine the sensitivities of the Greeks to various

parameters. For example, Figure 20.1 shows the deltas as functions of the

stock price, and Figure 20.2 shows them as functions of the moneyness

of the call option.

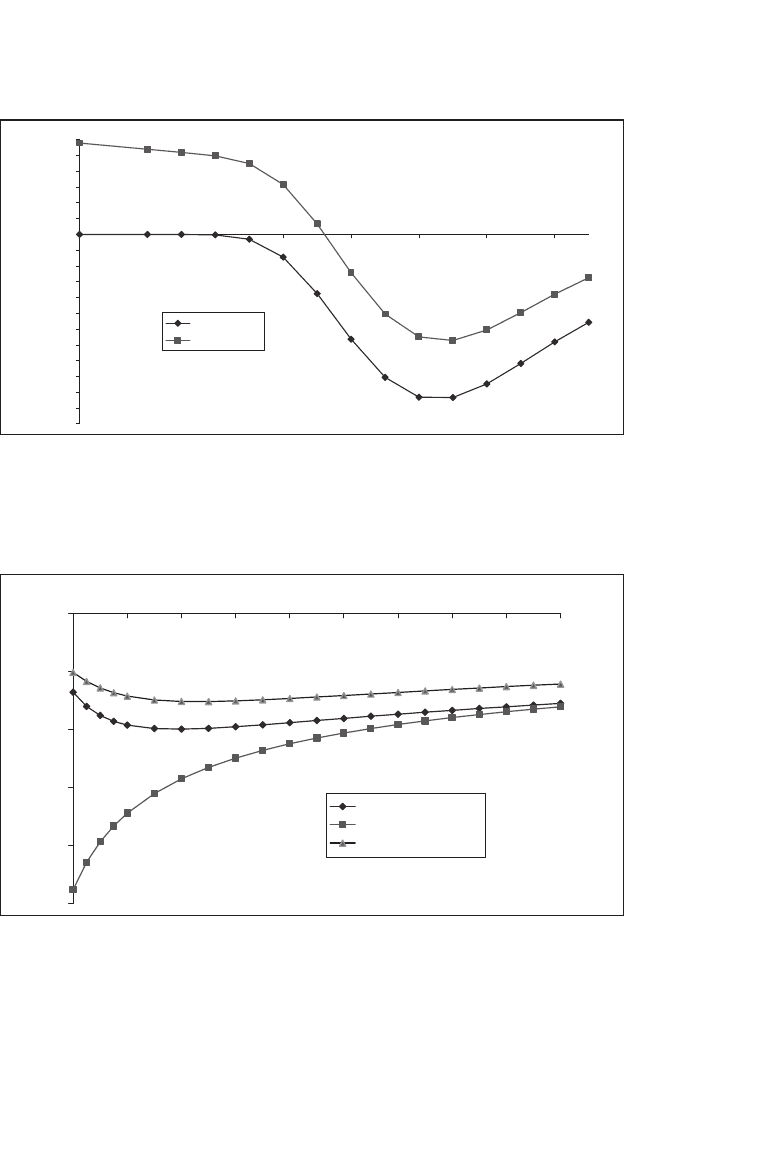
Figure 20.3 shows the theta of a call as a function of the stock price,

and Figure 20.4 shows it as a function of the time to option expiration.

20.3 Delta Hedging a Call

Delta hedging is a fundamental technique in option pricing. The idea is

to replicate an option by a portfolio of stocks and bonds, with the port-

folio proportions determined by the Black-Scholes formula.

Suppose we decide to replicate an at-the-money European call option

that has 12 weeks to run until expiration. The stock on which the option

is written has S

= $40 and exercise price X = $45, the interest rate is

AB C D E

S 100 Current stock price

X 90 Exercise price

T 0.5 Time to maturity of option (in years)

r 6.00% Risk-free rate of interest

k 2.00% Dividend yield

Sigma 35% Stock volatility

0.6303 <-- =(LN(B2/B3)+(B5-B6+0.5*B7^2)*B4)/(B7*SQRT(B4))

0.3828

<-- d

-sigma*SQRT(T)

N(d

)

0.7357

<-- Uses formula NormSDist(d

)

N(d

)

0.6491

<-- Uses formula NormSDist(d

)

Call price 16.1531 <-- =B2*EXP(-B6*B4)*B12-B3*EXP(-B5*B4)*B13

16.1531 <-- =bsmertoncall(B2,B3,B4,B5,B6,B7)

Put price 4.4882 <-- =B3*EXP(-B5*B4)*NORMSDIST(-B10)-B2*EXP(-B6*B4)*NORMSDIST(-B9)

4.4882 <-- =bsmertonput(B2,B3,B4,B5,B6,B7)

Greeks: Brute force

Call Put

Delta 0.7284 <-- =EXP(-B6*B4)*NORMSDIST(B9) -0.2616 <-- =-EXP(-B6*B4)*NORMSDIST(-B9)

Gamma 0.0195 <-- =EXP(B9^2/2-B6*B4)/(B2*B7*SQRT(2*B4*PI())) 0.0195 <-- =EXP((B9^2)/2-B6*B4)/(B2*B7*SQRT(2*B4*PI()))

Vega 22.8976 <-- =B2*SQRT(B4)*EXP(-(B9^2)/2)*EXP(-B6*B4)/SQRT(2*PI()) 22.8976 <-- =B2*EXP(-(B9^2)/2-B6*B4)*SQRT(B4)/SQRT(2*PI())

Theta -9.9587

<-- =-B2*EXP(-(B9^2)/2-

B6*B4)*B7/SQRT(8*B4*PI())+B6*B2*EXP(-B6*B4)*B12-

B5*B3*EXP

(-B5*B4)*B13

-6.6984

<-- =-B2*EXP(-(B9^2)/2-B6*B4)*B7/SQRT(8*B4*PI())-

B6*B2*EXP(-B6*B4)*(1-B12)+B5*B3*EXP(-B5*B4)*(1-

B13)

Rho 28.3446 <-- =B3*B4*EXP(-B5*B4)*NORMSDIST(B10) -15.3255 <-- =-B3*B4*EXP(-B5*B4)*NORMSDIST(-B10)

Greeks: VBA functions

Call Put

Delta 0.7284 <-- =deltacall(B2,B3,B4,B5,B6,B7) -0.2616 <-- =deltaput(B2,B3,B4,B5,B6,B7)

Gamma 0.0195 <-- =gamma(B2,B3,B4,B5,B6,B7) 0.0195 <-- =gamma(B2,B3,B4,B5,B6,B7)

Vega 22.8976 <-- =vega(B2,B3,B4,B5,B6,B7) 22.8976 <-- =vega(B2,B3,B4,B5,B6,B7)

Theta -9.9587

<-- =Thetacall(B2,B3,B4,B5,B6,B7)

-6.6984

<-- =Thetaput(B2,B3,B4,B5,B6,B7)

Rho 28.3446 <-- =rhocall(B2,B3,B4,B5,B6,B7) -15.3255 <-- =rhoput(B2,B3,B4,B5,B6,B7)

Black-Scholes Greeks

This spreadsheet uses the Merton model for a continuously dividend-paying stock

556 Chapter 20

Call and Put Deltas as Functions of Stock Price

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

0 20 40 60 80 100 120 140

Stock price

Delta

Call delta

Put delta

Call Delta, Time to Maturity, and Moneyness

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

Time to option expiration, T

Call delta

Out of the money

At the money

In the money

Figure 20.1

As a call or a put becomes more in-the-money, the delta tends toward +1 for a call and −1

for a put. Essentially the call or put price moves in tandem with the underlying stock price.

An extremely out-of-the-money put or call has a delta equal to 0.

Figure 20.2

As the option’s maturity T increases, the delta of an at-the-money or an out-of-the-money

call increases, whereas the delta of an in-the-money call decreases.

557 Option Greeks

Call and Put Thetas as Functions of Stock Price

Option Exercise Price = 100

-12

-11

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

0 20 40 60 80 100 120 140

Stock price

Theta

Call theta

Put theta

Call Theta, Time to Maturity, and Moneyness

-25

-20

-15

-10

-5

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

Time to option maturity

Theta

Out of the money

At the money

In the money

Figure 20.3

Very in-the-money puts can have a positive theta, meaning that as the time to maturity

gets shorter, the put gains in value. Other than this case, options generally have a negative

theta, meaning that they lose value as the time to maturity decreases.

Figure 20.4

Calls always have negative theta (meaning that they lose value as the time to maturity

decreases). However, the rate at which they lose value varies with the moneyness of the

call.