Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

538 Chapter 19

Payoff Goals puts

$1,000

Payment on Goal

−∗−

↑

25 641

25 641 39

.( )S

embedded puts

Payment on puts

purcha



+∗−

↑

25 641 39.( )S

ssed

$1,000



⎧

⎨

⎪

⎩

⎪

≥

$,1 000

In the following spreadsheet, we assume that the bought puts are

priced using Black-Scholes and compare the rate of return on this “engi-

neered” security to the risk-free rate:

AB C

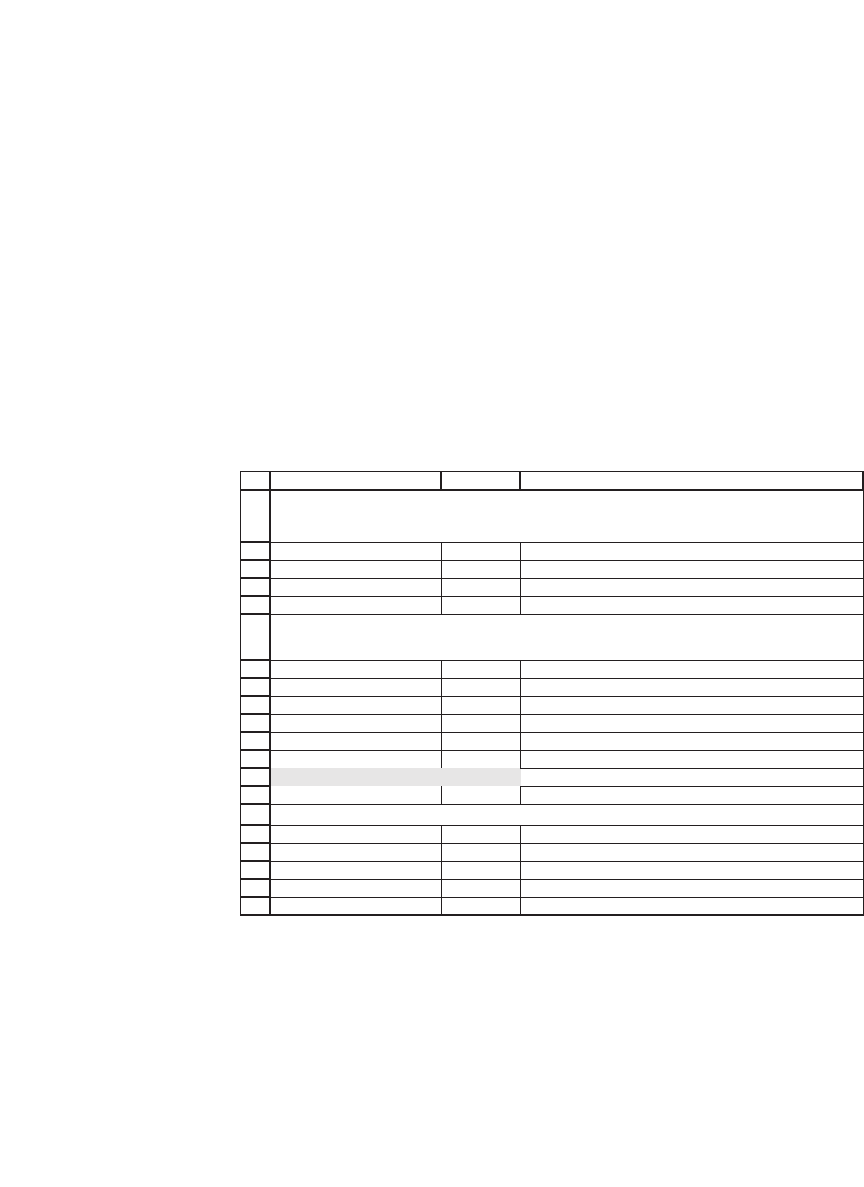
Initial cash flows

Buy UBS security -1,000.00

Buy 25.641 puts -300.21 <-- =-25.641*BSPut(B16,B17,B19,B18,B20)

Date Cash flow

23-Jan-01 (1,300.21) <-- =SUM(B3:B4)

23-Jul-01 97.50

23-Jan-02 97.50

23-Jul-02 1,097.50

IRR of above -0.43% <-- =XIRR(B8:B11,A8:A11)

Inputs for Black-Scholes formula in cell B4

S 42.625 Current stock price

X 39 Exercise price

r 5.20% Risk-free rate of interest

T 1.5 Time to maturity of option (in years)

Sigma 80% Stock volatility

CREATING A RISKLESS SECURITY WITH THE

UBS GOALS AND 25.641 PUTS

Cash flow of "engineered" security:

GOALS + 25.641 bought puts

Cell B13 uses the Excel function XIRR (see Chapter 34) to compute

the annualized internal rate of return on the engineered security. Clearly

this return is less than the alternative risk-free rate of return (5.2 percent)

that can be earned in the market. This is an alternative conﬁ rmation of

the fact that the Goals are a bad buy.

539 The Black-Scholes Model

19.8 Bang for the Buck with Options

This section presents another application of the Black-Scholes formula.

Suppose that you are convinced that a given stock will go up in a very

short period of time. You want to buy calls on the stock that have a

maximum “bang for the buck”—that is, you want the percentage proﬁ t

on your option investment to be maximal. Using the Black-Scholes

formula, it is easy to show that you should

•

Buy calls with the shortest possible maturity.

•

Buy calls that are most highly out of the money (i.e., with the highest

exercise price possible).

Here’s a spreadsheet illustration:

AB C

S 25 Current stock price

X 25 Exercise prie

r 6.00% Risk-free rate of interest

T 0.5 Time to maturity of option (in years)

Sigma 30% Stock volatility

0.2475 <-- (LN(S/X)+(r+0.5*sigma^2)*T)/(sigma*SQRT(T))

0.0354

<-- d

-sigma*SQRT(T)

N(d

)

0.5977

<-- Uses formula NormSDist(d

)

N(d

)

0.5141

<-- Uses formula NormSDist(d

)

Call price 2.47

<-- S*N(d

)-X*exp(-r*T)*N(d

)

Put price 1.73 <-- call price - S + X*Exp(-r*T): by put-call parity

Call bang 6.0483 <-- =B11*B2/B14

Put bang 5.8070 <-- =NORMSDIST(-B8)*B2/B15

"BANG FOR THE BUCK" WITH OPTIONS

The “call bang” deﬁ ned in cell B17 is simply the percentage change in

the call price dividend by the percentage change in the stock price (in

economics this is known as the price elasticity):

540 Chapter 19

Call bang

∂

()

Similarly, for a put, the “bang for the buck” is deﬁ ned by the following

formula (of course, the story behind the put “bang for the buck” is that

you are convinced that the stock price will go down):

Put bang

∂

=− −

()

This is deﬁ ned in cell B18. To make the numbers easier to understand,

we have dropped the minus sign, making the “put bang” =

()−

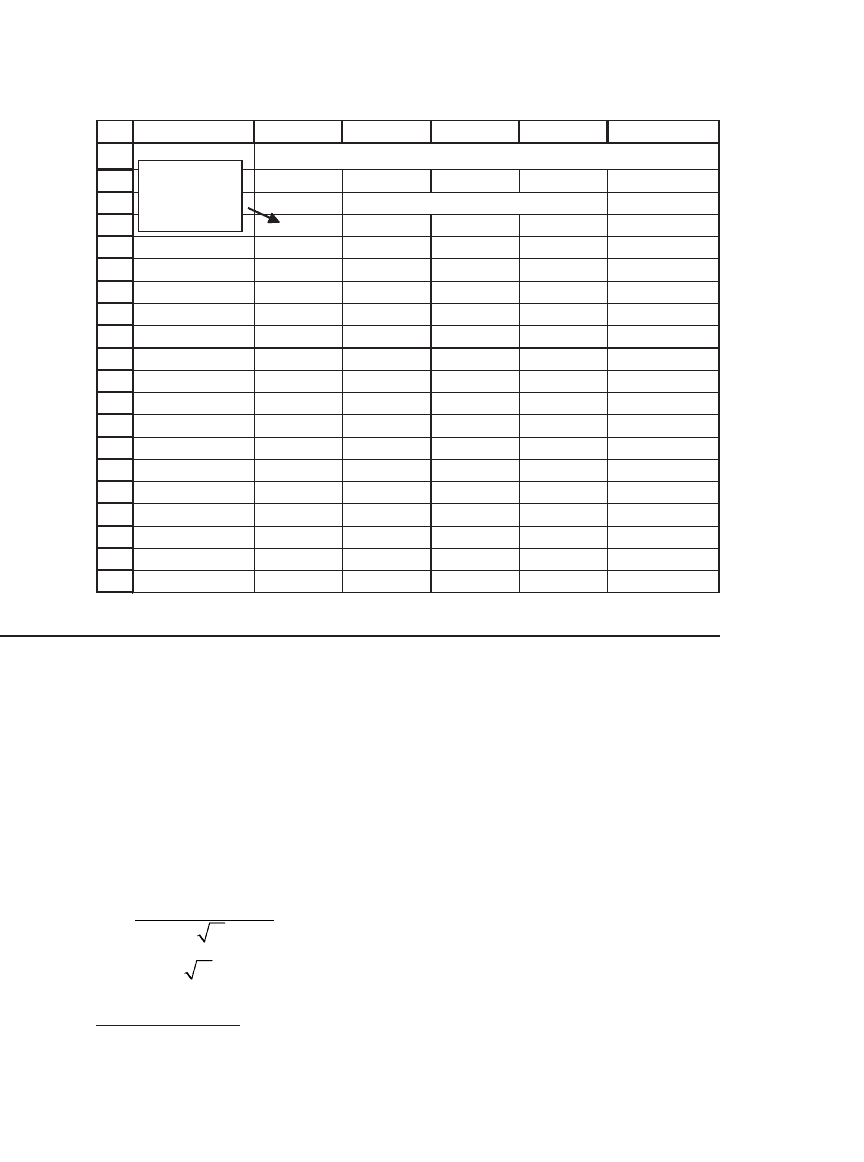
The following graph shows the “bang for the buck” for both calls and

puts:

"Bang for the Buck"

The Price Elasticity of Calls and Puts

as a Function of the Exercise Price X

15 17 19 21 23 25 27 29 31

Option exercise price, X ($)

Pofit elasticity--"bang"

Calls

Puts

If you play with the spreadsheet, you will see that the longer the time to

maturity, the less the bang for the buck. (Another way of saying all this

is that the most risky options are the most out-of-the-money and the

shortest-term options.)

541 The Black-Scholes Model

19.9 The Black (1976) Model for Bond Option Valuation

Black (1976) suggested an adaptation of the Black-Scholes model, which

is often used for simple valuation of options on bonds or forwards.

Letting F stand for the forward price of an asset, the Black-Scholes equa-

tion given in section 19.2 is replaced by

Ce FNd XNd

=−

−

[() ()]

where

FX T

+ln / /2()

dd T

=−

DEFGHI

Data table: Effect of S and T on "call bang"

T--option time to exercise

6.0483

0.25 0.5 0.75 1

25.8856 14.1771 10.1696 8.1112

23.3305 12.9884 9.4123 7.5625

20.9954 11.9033 8.7218 7.0623

18.8590 10.9121 8.0914 6.6057

16.9052 10.0067 7.5154 6.1882

15.1222 9.1805 6.9891 5.8062

13.5007 8.4274 6.5082 5.4565

12.0334 7.7424 6.0691 5.1362

10.7137 7.1205 5.6682 4.8426

9.5347 6.5572 5.3025 4.5737

8.4893 6.0483 4.9691 4.3272

7.5694 5.5896 4.6655 4.1012

6.7664 5.1773 4.3892 3.8941

6.0706 4.8074 4.1379 3.7043

5.4720 4.4764 3.9094 3.5303

4.9598 4.1807 3.7019 3.3708

Data table

header:

=B17

6. This section is advanced and can be skipped on ﬁ rst reading. A full discussion of the

pricing of bond options is beyond the scope of the current edition of this book.

However, this very useful and often-used adaptation of the Black model is simple

enough to attach to this chapter.

542 Chapter 19

The corresponding put price is given by

Pe XNd FNd

=−−−

−

[() ()]

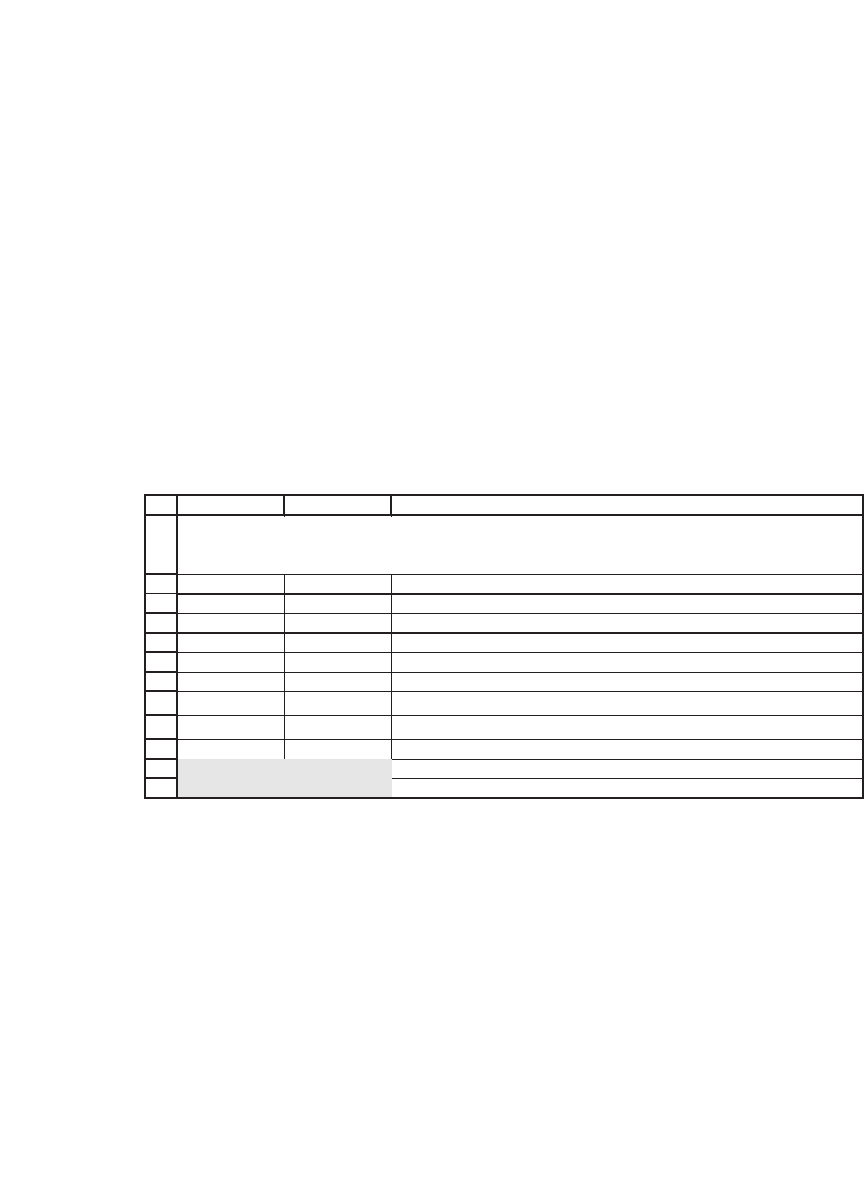
To use the Black (1976) model, consider the case of an option on a

zero coupon bond, where the option maturity is T = 0.5. The option gives

the holder the opportunity to buy the bond at time T for exercise price

X = 130. Suppose that the risk-free interest rate is r = 4 percent. If the

forward price of the bond to the exercise date is F = 133 and the volatility

of the forward price is σ = 6 percent, then the pricing of the bond option

using the Black (1976) model is as follows:

AB C

F 133.011 <-- Bond forward price

X 130.000 <-- Exercise price

r 4.00% <--Risk-free rate of interest

0T.5

Sigma 6%

<-- Bond forward price volatility,

0.5609 <-- =(LN(B2/B3)+B6^2*B5/2)/(B6*SQRT(B5))

0.5185 <-- =B8-SQRT(B5)*B6

Call price 4.13 <-- =EXP(--B4*B5)*(B2*NORMSDIST(B8)-B3*NORMSDIST(B9))

Put price 1.02 <-- =EXP(-B4*B5)*(B3*NORMSDIST(-B9)-B2*NORMSDIST(-B8))

USING THE BLACK (1976) MODEL

TO PRICE A BOND OPTION

Thus a call on the bond is worth 4.13 and a put is worth 1.02.

19.9.1 Determining the Bond’s Forward Price

The forward interest rate is the interest rate that can be locked in

today for a loan in the future. In the next example, the current 7-year

rate is 6 percent and the 4-year rate is 5 percent. By simultaneously

creating a deposit in one maturity and a loan in the other maturity, we

create a security that has zero cash ﬂ ows everywhere except at years

4 and 7:

543 The Black-Scholes Model

The preceding spreadsheet shows two forward rate computations. If

the interest rates are discretely compounded, then the forward rate from

year 4 to year 7 is given by

Discretely compounded

forward rate, year 4 to 7

⎡

⎣

⎢

()

⎤⎤

⎦

⎥

−

⎡

⎣

⎢

⎤

⎦

⎥

−=

⎛

⎝

⎜

⎞

⎠

⎟

(/)

(%)

1 5036

1 2155

((

1/3)

−=1735

If the rates are continuously compounded (as in the Black model

and most option calculations) then the forward rate from year 4 to 7 is

given by

Continously compounded

forward rate, year 4 to 7

Ln=

⎛

⎝

⎜

⎞

⎠

⎟

∗

1 5220

1 221

∗

⎡

⎣

⎢

⎤

⎦

⎥

⎛

⎝

⎜

⎞

⎠

⎟

⎡

⎣

⎢

⎤

⎦

⎥

⎛

⎝

⎜

⎞

⎠

⎟

733

⎛

⎝

⎜

⎞

⎠

⎟

= .%

To apply the forward interest rate to the example in the previous

subsection, assume that the bond in question has a maturity of two years

and a face value at maturity of 147. Then if the 2-year interest rate is r

= 6 percent and the interest rate to the option’s maturity is r

0.5

= 4 percent,

the forward price of the bond is F = 133.011, as shown here:

BACDEFGHI

Bond maturity, W 7

Option maturity, T 4

Year W pure discount rate 6%

Year T pure discount rate 5%

Discretely-compounded interest rates

012345678

7-year deposit at 6.00% 100.00 -150.36

4-year loan at 5.00% -100.00 121.55

Sum of above: A 3-year deposit at year 4 0.00 121.55 -150.36

Discretely-compounded forward interest rate

from

year 4 to year 7

7.35% <-- =(-I11/F11)^(1/(B2-B3))-1

Continuously-compounded interest rates

012345678

7-year deposit at 6.00% 100.00 -152.20

4-year loan at 5.00% -100.00 122.14

Sum of above: A 3-year deposit at year 4 0.00 122.14 -152.20

Continuously-compounded forward interest

rate from year 4 to year 7

7.33% <-- =LN(-I19/F19)/(B2-B3)

THE FORWARD INTEREST RATE

544 Chapter 19

19.10 Summary

The Black-Scholes formula for pricing options is one of the most power-

ful innovations in ﬁ nance. The formula is widely used both to price

options and as a conceptual framework for analyzing complex securities.

In this chapter we have explored the implementation of the Black-

Scholes formula. Using “plain vanilla” Excel allows us to price Black-

Scholes options; using VBA we are able to deﬁ ne both the Black-Scholes

price and the implied volatility for options. Finally, we showed how to

use Black-Scholes to price structured products—combinations of options,

stocks, and bonds.

Exercises

1. Use the Black-Scholes model to price the following:

a. A call option on a stock whose current price is 50, with exercise price X = 50,

T = 0.5, r = 10 percent, σ = 25 percent.

b. A put option with the same parameters.

2. Use the data from exercise 1 and Data|Table to produce graphs that show

a. The sensitivity of the Black-Scholes call price to changes in the initial stock price

b. The sensitivity of the Black-Scholes put price to changes in σ.

c. The sensitivity of the Black-Scholes call price to changes in the time to maturity

d. The sensitivity of the Black-Scholes call price to changes in the interest rate r.

e. The sensitivity of the put price to changes in the exercise price X.

CBA

Bond's maturity, N 2

Option maturity, T 0.5

Bond maturity value 147

Interest rate to N 6%

Interest rate to T 4%

Bond forward price to T 133.011 <-- =B4*EXP(-B6*B2)*EXP(B7*B3)

DETERMINING THE FORWARD PRICE

OF THE BOND

545 The Black-Scholes Model

3. Produce a graph comparing a call’s intrinsic value [deﬁ ned as max(S − X, 0)] and

its Black-Scholes price. From this graph you should be able to deduce that it is never

optimal to exercise a call priced by the Black-Scholes early.

4. Produce a graph comparing a put’s intrinsic value [max(X − S, 0)] and its Black-

Scholes price. From this graph you should be able to deduce that it may be optimal

to exercise a put priced by the Black-Scholes formula early.

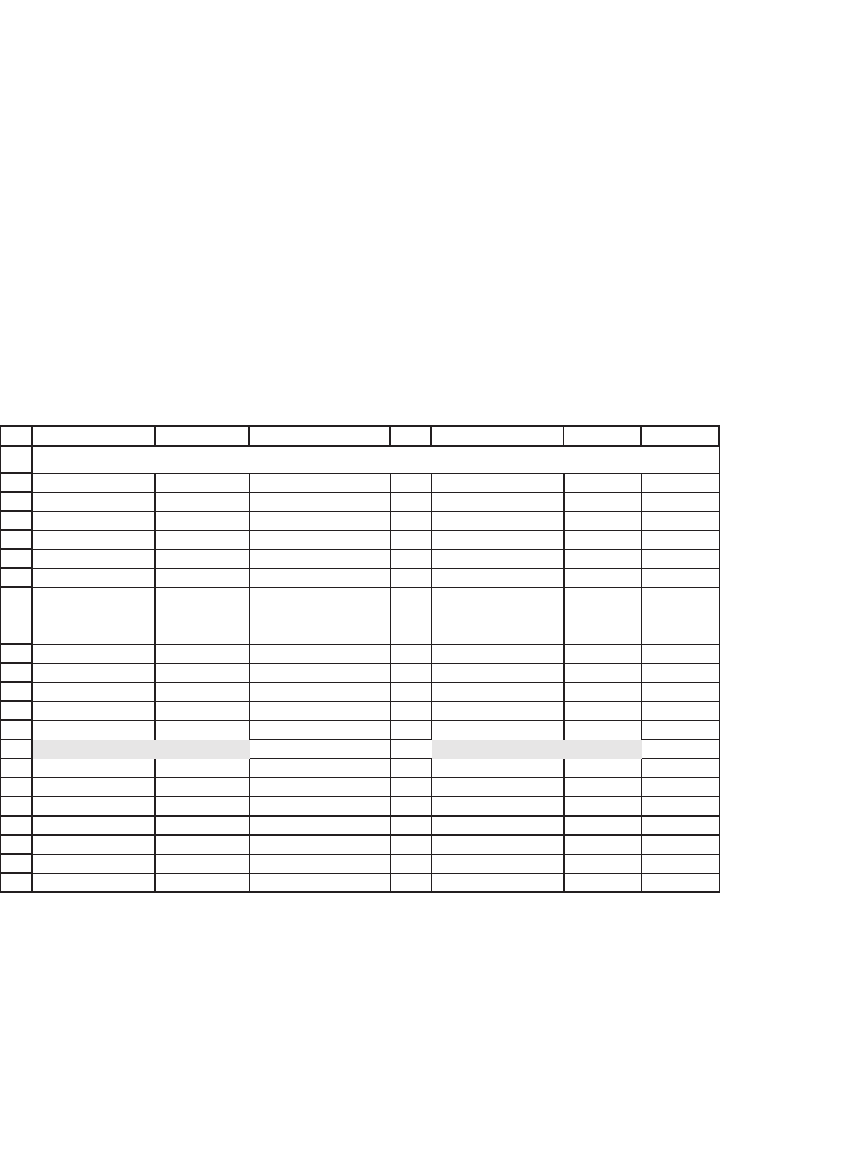
5. The following table gives prices for American Airlines (AMR) options on 12 July

2007. The option with exercise price X = $27.50 is assumed to be the at-the-money

option.

a. Compute the implied volatility of each option (use the functions CallVolatility

and PutVolatility deﬁ ned in the chapter).

b. Graph these volatilities. Is there a volatility “smile”?

AB CDEFG

Stock price 27.82

Current date 12-Jul-07

Expiration date 16-Nov-07

Time to maturity, 0.35 <-- =(B4-B3)/365

Interest 5%

Strike

Call option

price

Implied volatility Strike

Put

option

price

Implied

volatility

51.00.5105.310.51

52.05.7104.015.71

55.00.0204.80.02

60.15.2202.75.22

09.10.5209.40.52

59.25.7203.35.72

03.40.0303.20.03

01.65.2356.15.23

04.70.5300.10.53

06.95.7307.05.73

07.210.0454.00.04

45.0 0.25

50.0 0.05

AMR OPTIONS

6. Re-examine the X = 17.50 call for AMR in the previous exercise.

a. Is the call correctly priced?

b. What price would be necessary for this call in order for the implied volatility to

be 60%?

7. Use the Excel Solver to ﬁ nd the stock price for which there is the maximum differ-

ence between the Black-Scholes call option price and the option’s intrinsic value.

Use the following values: S = 45, X = 45, T = 1, σ = 40 percent, r = 8 percent.

546 Chapter 19

8. As shown in this chapter, Merton (1973) shows that for the case of an asset with

price S paying a continuously compounded dividend yield k, leads to the following

call option pricing formula:

CSe Nd XeNd

kT rT

=−

−−

() (),

where

SX r k T

+−+ln / /2)()(

dd T

=−

a. Modify the BSCall and BSPut functions deﬁ ned in this chapter to ﬁ t the Merton

model.

b. Use the function to price an at-the-money option on an index whose current

price is S = 1,500, when the option’s maturity T = 1, the dividend yield is k = 2.2

percent, its standard deviation σ = 20 percent, and the interest rate r = 7

percent.

9. On 12 July 2007, call and put options to purchase and sell 10,000 euros at $1.37 per

euro are traded on the Philadelphia options exchange. The options’ expiration date

is 20 December 2007. If the dollar interest rate is 5 percent, the euro interest rate

is 4.5 percent and the volatility of the euro is 6 percent, what should be the price of

a call and a put?

10. Note that you can use the Black-Scholes formula to calculate the call option

premium as a percentage of the exercise price in terms of S/X:

C SNd Xe Nd

Nd e Nd

rT rT

=− ⇒= −

−−

() () () ()

12 12

where

SX r T

++ln / /2)()(

dd T

=−

Implement this formula in a spreadsheet.

11. Note that you can also calculate the Black-Scholes put option premium as a percent-

age of the exercise price in terms of S/X:

P SNd Xe Nd

eNd

rT rT

=− − + − ⇒ = − − −

−−

() () () ()

12 21

where

SX r T

++ln / /2()( )

dd T

=−

Implement this formula in a spreadsheet. Find the ratio of S/X for which C/X and

P/X cross when T = 0.5, σ = 25 percent, r = 10 percent. (You can use a graph or you

547 The Black-Scholes Model

can use Excel’s Solver.) Note that this crossing point is affected by the interest rate

and the option maturity, but not by σ.

12. Consider a structured security of the following type: The purchaser invests $1,000

and in three years gets back the initial investment, plus 95 percent of the increase

in a market index whose current price is 100. The interest rate is 6 percent per year,

continuously compounded. Assuming the security is fairly priced, what is the implied

volatility of the market index?