Simon Benninga. Financial Modelling 3-rd edition
Подождите немного. Документ загружается.


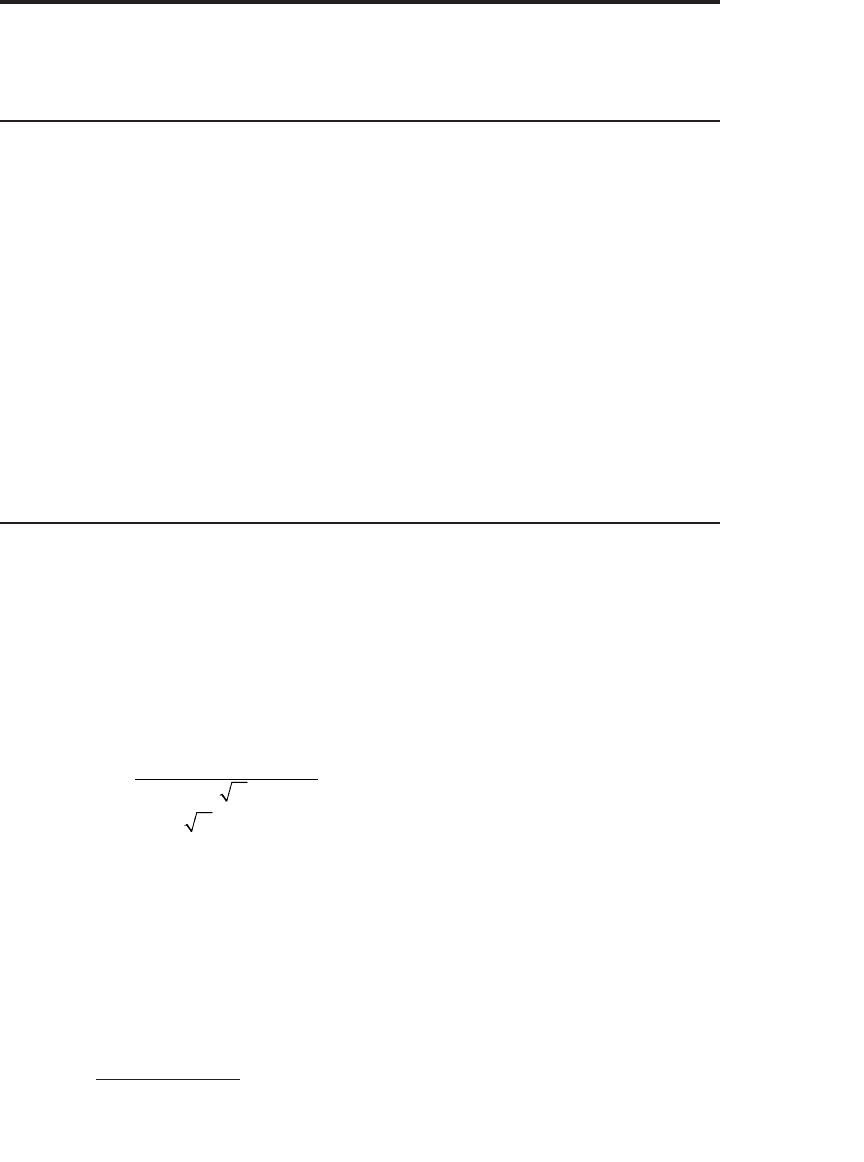
19
The Black-Scholes Model
19.1 Overview
In a pathbreaking paper published in 1973, Fisher Black and Myron
Scholes proved a formula for pricing European call and put options on
non-dividend-paying stocks. Their model is probably the most famous
model of modern fi nance. The Black-Scholes formula is relatively easy
to use, and it is often an adequate approximation to the price of more
complicated options.
In this chapter we make no pretense at a full-blown development of
the model; this requires a knowledge of stochastic processes and a not-
inconsiderable mathematical investment. Instead, we shall describe the
mechanics of the model and show how to implement it in Excel. We also
illustrate several uses of the Black-Scholes formula in the valuation of
structured assets.
19.2 The Black-Scholes Model
Consider a stock whose price is lognormally distributed.
1
The Black-
Scholes model uses the following formula to price European calls on a
stock:
C SNd Xe Nd
rT
=−
−
() ()
12
where
d
SX r T
T
dd T
1
2
21
=
++
=−
ln / /2)()(
σ
σ
σ
Here C denotes the price of a call, S is the price of the underlying
stock, X is the exercise price of the call, T is the call’s time to exercise, r
is the interest rate, and σ is the standard deviation of the logarithm of
the stock’s return. N( ) denotes a value of the standard normal distribu-
tion. It is assumed that the stock will pay no dividends before date T.
By the put-call parity theorem (see Chapter 16), a put with the same
exercise date T and exercise price X written on the same stock will have
1. The lognormal distribution is discussed in Chapter 18.
510 Chapter 19
price P = C − S + Xe
−rT
. Substituting for C in this equation and doing
some algebra gives the Black-Scholes European-put-pricing formula:
PXeNd SNd
rT
=−−−
−
() ()
21
We note that in Chapter 17 we hinted at one form of the proof of the
Black-Scholes formula. There it was shown numerically that the Black-
Scholes formula coincides with the binomial option-pricing model
formula when (1) the length of a typical period approaches 0, (2) the
“up” and “down” moves in the binomial model converge to a lognormal
price process, and (3) the term structure of interest rates is fl at.
19.2.1 Implementing the Black-Scholes Formulas in a Spreadsheet
The Black-Scholes formulas for call and put pricing are easily imple-
mented in a spreadsheet. The following example shows how to calculate
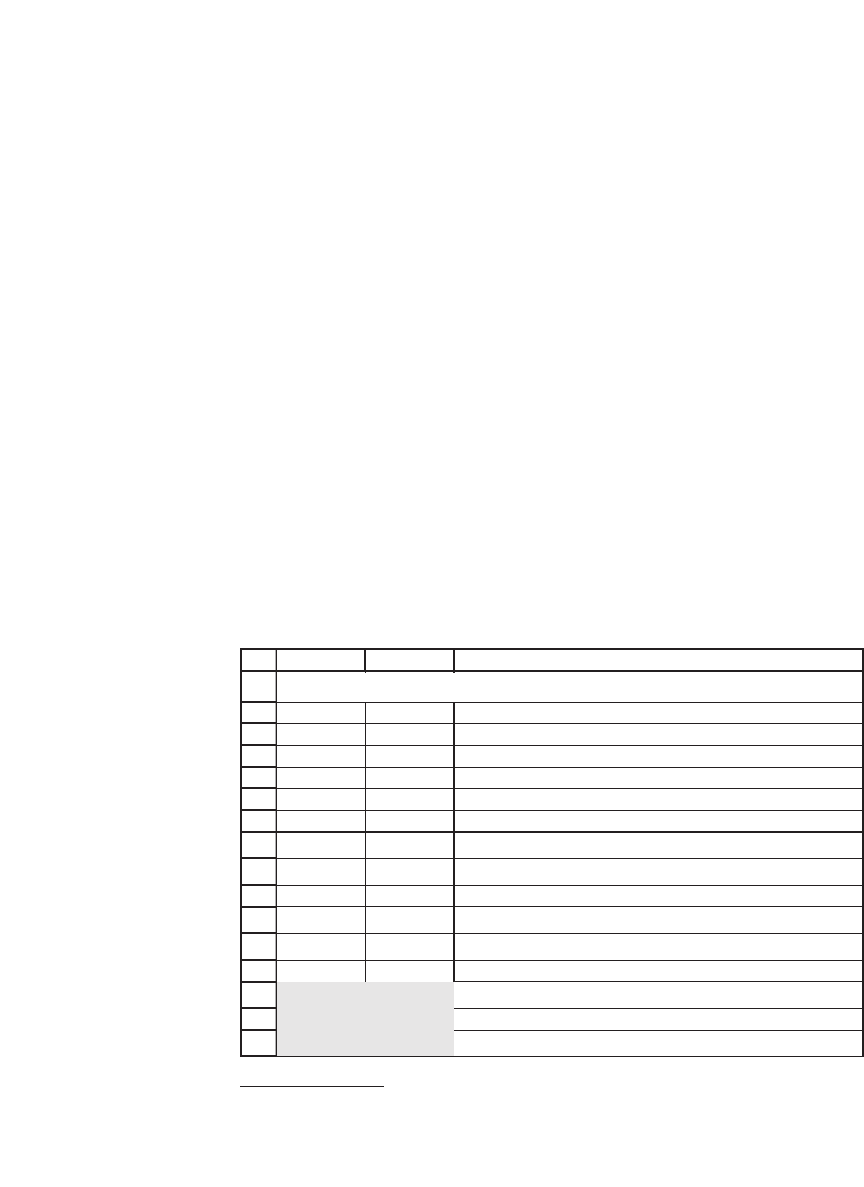
the price of a call option written on a stock whose current price S = 50,
when the exercise price X = 45, the annualized interest rate r = 4 percent,
and σ = 30 percent. The option has T = 0.75 years to exercise. All three
of the parameters T, r, and σ are assumed to be in annual terms.
2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
AB C
S 50 Current stock price
X 45 Exercise price
r 4.00% Risk-free rate of interest
T 0.75 Time to maturity of option (in years)
Sigma 30%
Stock volatility,
σ
d
1
0.6509 <-- (LN(S/X)+(r+0.5*sigma^2)*T)/(sigma*SQRT(T))
d
2
0.3911
<-- d
1
-sigma*SQRT(T)
N(d
1
)
0.7424
<-- Uses formula NormSDist(d
1
)
N(d
2
)
0.6521
<-- Uses formula NormSDist(d
2
)
Call price 8.64
<-- S*N(d
1
)-X*exp(-r*T)*N(d
2
)
Put price 2.31 <-- call price - S + X*Exp(-r*T): by Put-Call parity
2.31
<-- X*exp(-r*T)*N(-d
2
) - S*N(-d
1
): direct formula
Black-Scholes Option-Pricing Formula
2. Section 18.7 discusses how to calculate the annualized σ of the lognormal process given
nonannual data.
511 The Black-Scholes Model
The spreadsheet calculates the put price twice: In cell B15 the put price
is computed by using put-call parity, and in cell B16 it is calculated by
using the direct Black-Scholes formula.
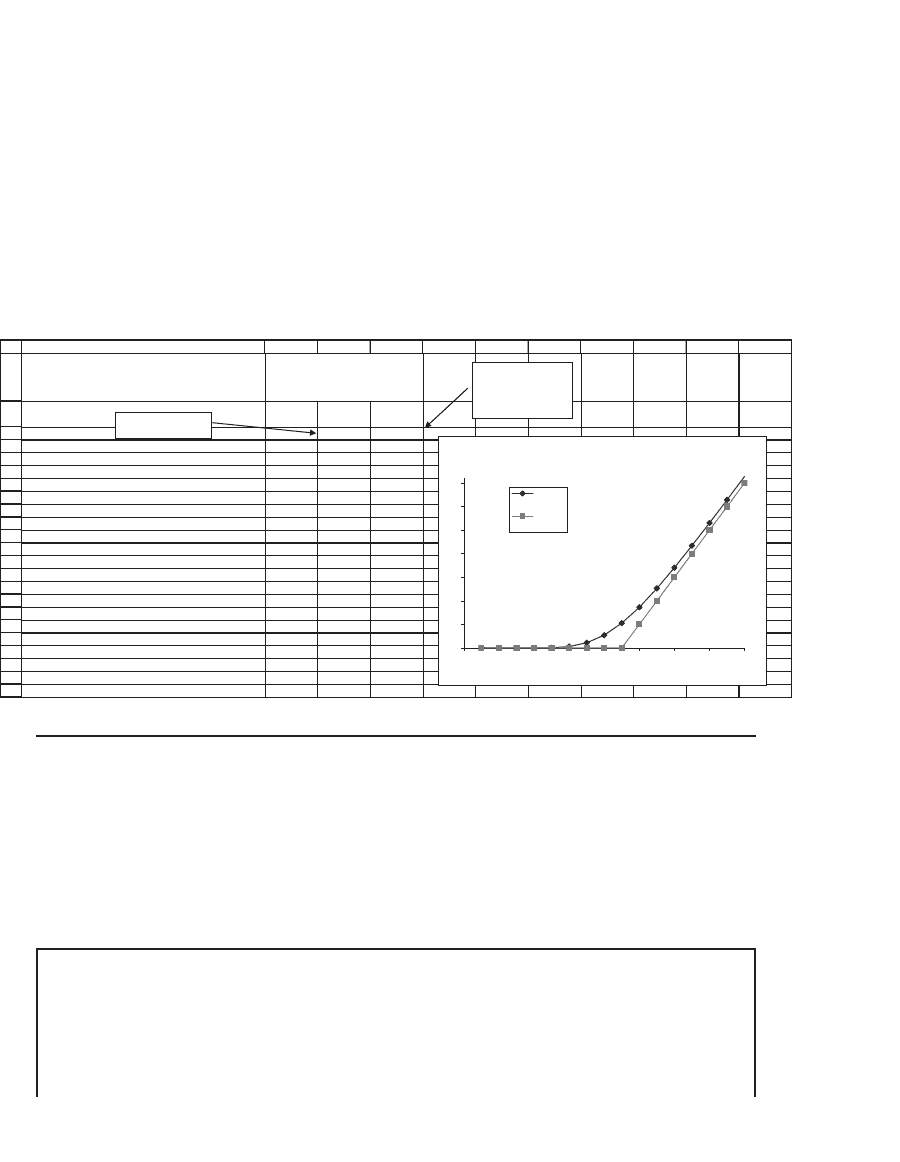
We can use this spreadsheet to do the usual sensitivity analysis. For
example, the following Data|Table (see Chapter 31) gives—as the stock
price S varies—the Black-Scholes value of the call compared to its intrin-
sic value [i.e., max(S − X, 0)].
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
DCEFGHIJKL
Stock
price
Call
price
Intrinsic
value
8.6434 5
5 0.0000 0
10 0.0000 0
15 0.0000 0
20 0.0029 0
25 0.0484 0
30 0.3101 0
35 1.1077 0
40 2.7319 0
45 5.2777 0
50 8.6434 5
55 12.6307 10
60 17.0378 15
65 21.7056 20
70 26.5256 25
75 31.4304 30
80 36.3811 35
Data table: Comparing
the Black-Scholes
to the intrinsic value
M
Black-Scholes Price versus Instrinsic Value
0
5
10
15
20
25
30
35
0 1020304050607080
Stock price, S
Call
price
Intrinsic
value
Data table header:
= B14
Data table header:
=Max(B2-B3,0).
This is the option's
intrinsic value
.
19.3 Using VBA to Defi ne a Black-Scholes Pricing Function
Although the spreadsheet implementation of the Black-Scholes formu-
las illustrated in the previous section is suffi cient for some purposes, we
are sometimes interested in having a closed-form function that we can
use directly in Excel. We can do so with Visual Basic for Applications. In
the following program we defi ne functions dOne, dTwo, and BSCall:
Function dOne(Stock, Exercise, Time, Interest, sigma)
dOne = (Log(Stock / Exercise) + Interest * _
Time) / (sigma * Sqr(Time)) _
+ 0.5 * sigma * Sqr(Time)
End Function

512 Chapter 19
Note the use of the Excel function NormSDist, which gives the standard
normal distribution; in order to use this function in VBA, we must write
Application.NormSDist.
19.3.1 Pricing Puts
By the put-call parity theorem we know that a put is priced by the
formula P = C − S + Xe
−rT
. We can implement this in another VBA
function, BSPut:
Function dTwo(Stock, Exercise, Time, Interest, sigma)
dTwo = dOne(Stock, Exercise, Time, Interest, _
sigma) - sigma * Sqr(Time)
End Function
Function BSCall(Stock, Exercise, Time, Interest, sigma)
BSCall = Stock * Application.NormSDist(dOne(Stock, _
Exercise, Time, Interest, sigma)) - _
Exercise * Exp(-Time * Interest) * _
Application.NormSDist(dTwo(Stock, Exercise, _
Time, Interest, sigma))
End Function
Function BSPut(Stock, Exercise, Time, Interest, sigma)
BSPut = BSCall(Stock, Exercise, Time, Interest, _
sigma) + Exercise * Exp(-Interest * Time) - Stock
End Function
19.3.2 Using These Functions in an Excel Spreadsheet
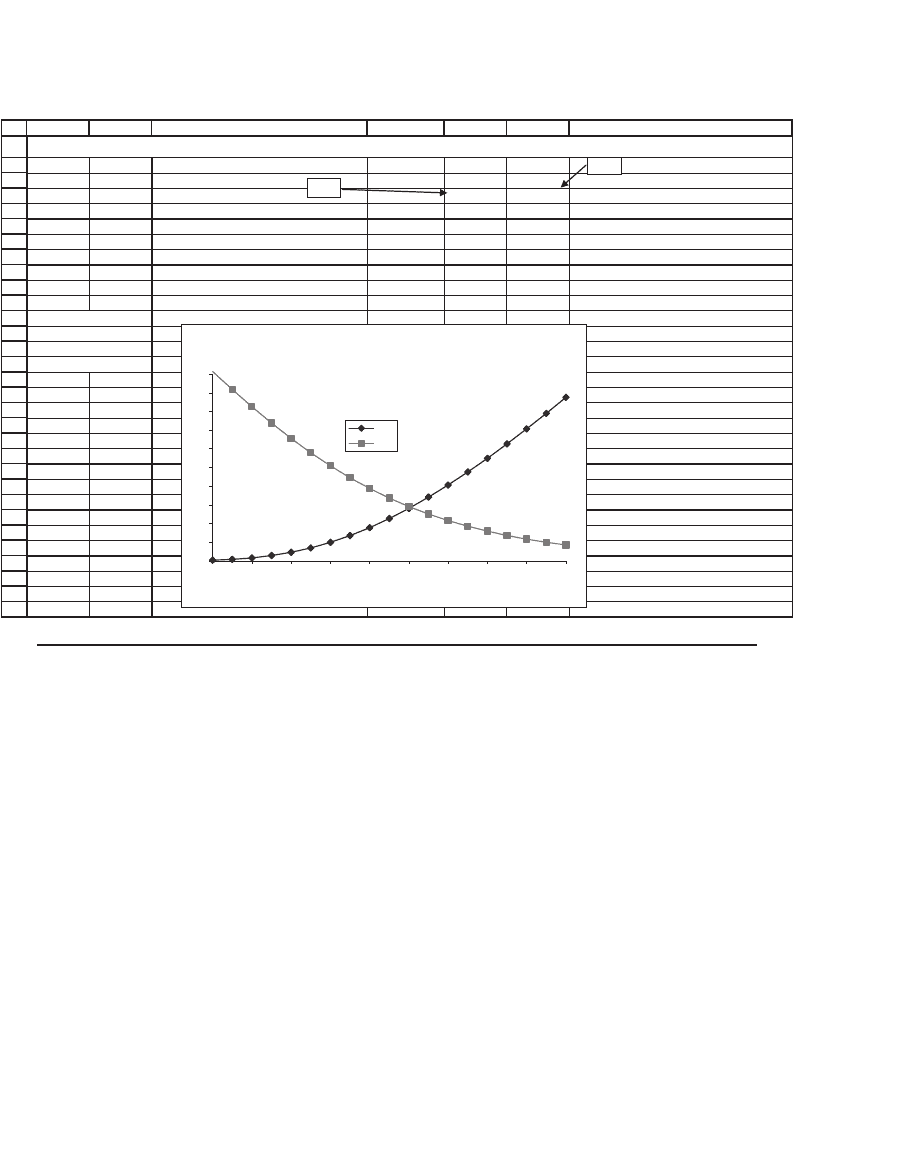
Here’s an example of these functions used in Excel. The graph was
created by a data table. (In presentations we usually hide the fi rst row
of such a table; here we have shown it.)
513 The Black-Scholes Model
19.4 Calculating the Implied Volatility
The Black-Scholes formula depends on fi ve parameters: The stock price
S, the option exercise price X, the option’s time to maturity T, the interest
rate r, and the standard deviation of the returns of the stock underlying
the option σ (sigma). Four of these fi ve parameters are straightforward,
but the fi fth parameter, σ, is problematic. There are two common ways
of computing σ:
•
σ can be computed based on the historical returns of the stock.
•
σ can be computed based on the implied volatility of the stock.
In the two subsections that follow, we illustrate both methods of comput-
ing σ.
19.4.1 The Sigma of Historical Returns
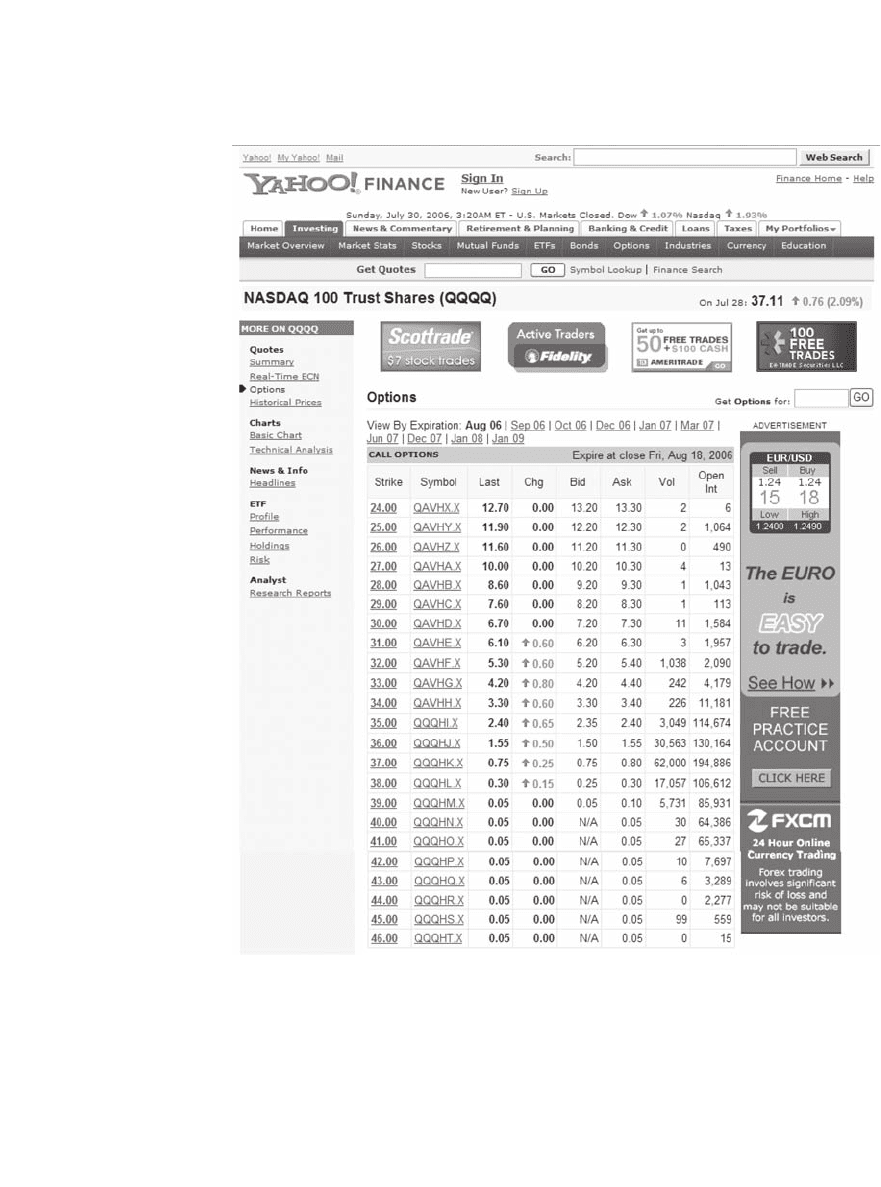
We examine the option prices on the Nasdaq index QQQQ on 28 July 2006.
A complete listing of these prices (from Yahoo) is given in Figure 19.1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
AB C D EF G
S100
X100
Stock price Call Put
T 1.00 20.3185 10.8022 <--This is the header of the Data Table
Interest 10.00% 40 0.1802 50.6639
Sigma 40.00% 45 0.4104 45.8941
50 0.8081 41.2918
Call price 20.3185 <-- =BSCall(B2,B3,B4,B5,B6) 55 1.4241 36.9079
Put price 10.8022 <-- =BSPut(B2,B3,B4,B5,B6) 60 2.3019 32.7857
65 3.4739 28.9576
70 4.9600 25.4437
To the right is a data 75 6.7683 22.2520
table that gives the 80 8.8965 19.3803
call and put values for 85 11.3341 16.8179
various stock 90 14.0645 14.5482
6055.219660.7159 .secirp
100 20.3185 10.8022
105 23.7954 9.2791
110 27.4740 7.9578
115 31.3316 6.8154
120 35.3469 5.8306
125 39.5002 4.9839
130 43.7736 4.2574
BLACK-SCHOLES MODEL IN VBA
=B8
=B9
Call and Put Prices Using Black-Scholes
0
5
10
15
20
25
30
35
40
45
50
40 50 60 70 80 90 100 110 120 130
Stock price, S
Call
Put
514 Chapter 19
Figure 19.1
QQQQ index call prices, 28 July 2006. The highlighted prices are for in-the-money
options.
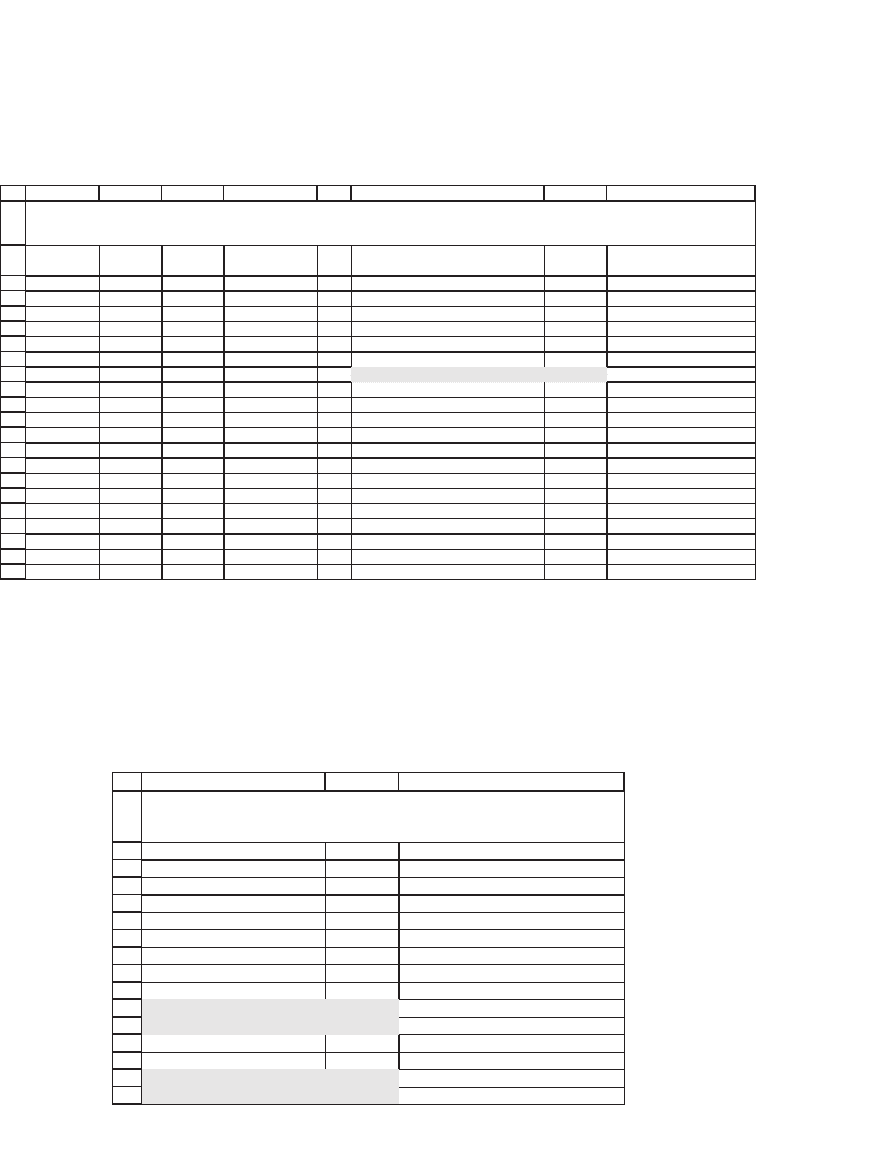
515 The Black-Scholes Model
The historical prices of the QQQQ and the resulting historical volatil-
ity are computed in the next spreadsheet:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
38
39
40
41
42
43
44
45
ABC DE F G H
Date
Closing
price
Return
30-May-06 38.61
31-May-06 38.79 0.47% <-- =LN(B4/B3)
Return statistics
1-Jun-06 39.71 2.34% <-- =LN(B5/B4) Average daily return -0.09% <-- =AVERAGE(C4:C45)
2-Jun-06 39.61 -0.25% <-- =LN(B6/B5) Standard deviation of daily return 1.31% <-- =STDEVP(C4:C45)
5-Jun-06 38.75 -2.20% <-- =LN(B7/B6)
6-Jun-06 38.72 -0.08% Annualized mean return -23.59% <-- =250*G5
7-Jun-06 38.43 -0.75% Annualized sigma 20.66% <-- =G6*SQRT(250)
8-Jun-06 38.37 -0.16%
9-Jun-06 38.12 -0.65%
12-Jun-06 37.37 -1.99%
13-Jun-06 37.22 -0.40%
14-Jun-06 37.6 1.02%
19-Jul-06 36.62 1.29%
20-Jul-06 36.08 -1.49%
21-Jul-06 35.7 -1.06%
24-Jul-06 36.41 1.97%
25-Jul-06 36.62 0.58%
26-Jul-06 36.59 -0.08%
27-Jul-06 36.35 -0.66%
28-Jul-06 37.11 2.07%
QQQQ HISTORICAL PRICES, DAILY DATA
and resulting statistics
Based on two months of daily data, the annualized QQQQ sigma is
20.66 percent. Note that this result is based on the assumption of 250
trading days per year; many traders use 365 days, which would of course
give a higher σ. Based on this volatility, the at-the-money QQQQ August
2006 call would be priced at 0.85 and the QQQQ August 2006 put would
be priced at 0.63 (cell B12):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
AB C
Current date 28-Jul-06
Option expiration date 18-Aug-06
3S 7.11
3X7
T 0.06 <-- =(B3-B2)/365
Interest 5.00%
Sigma 20.66%
Call price 0.8447 <-- =BSCall(B5,B6,B7,B8,B9)
Put price 0.6284 <-- =BSPut(B5,B6,B7,B8,B9)
Actual prices
Call 0.75
Put 0.55
PRICING THE AUGUST 2006 QQQQ OPTIONS
σ
Using the Historical Volatility
σ
516 Chapter 19
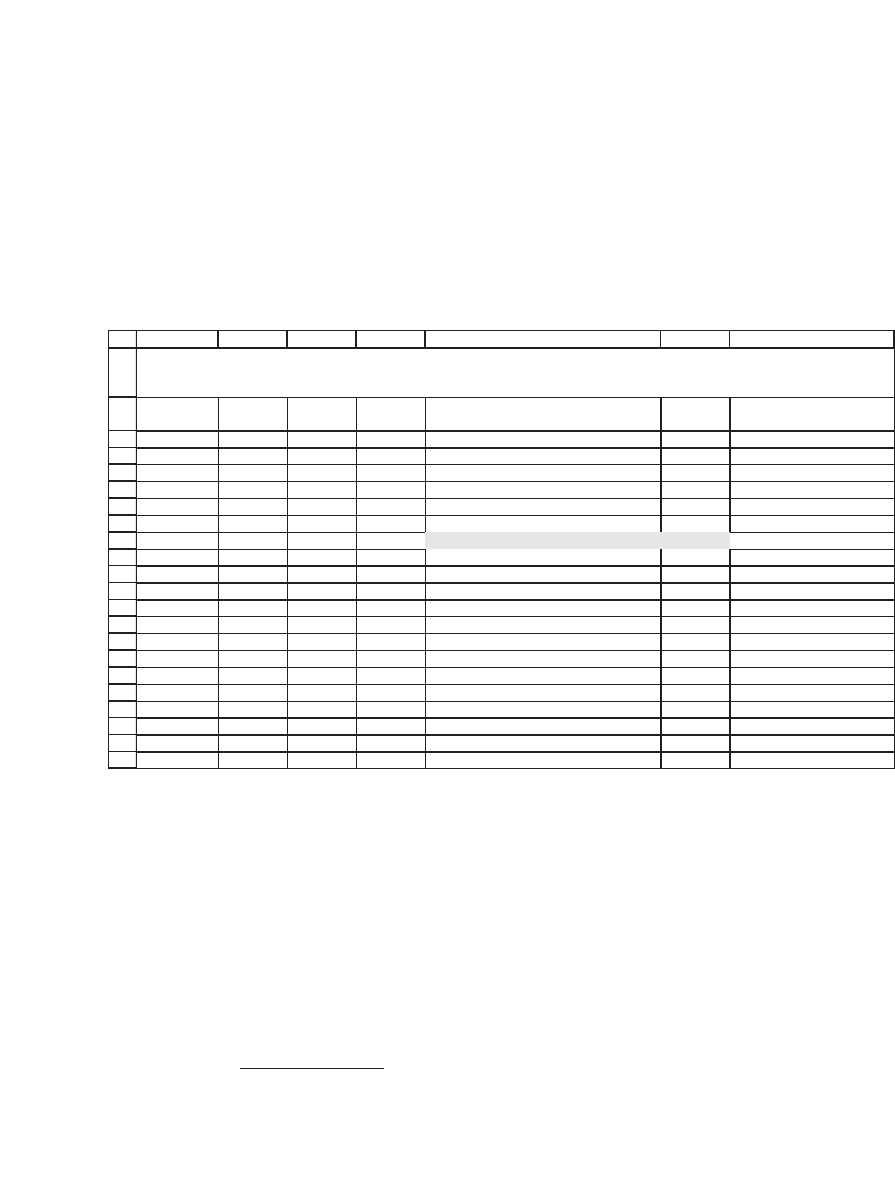
Compared to the actual prices, this picture seems to indicate that the
historical volatility somewhat overstates the volatility at which the
options are actually priced. Note, however, that it is not clear which data
are the correct historical data. If, for example, we were to use two years
of monthly data to determine the historical volatility for the QQQQ, we
would arrive at a much lower number:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
38
39
40
41
42
43
44
45
ABCD E F G
Date
Closing
p
rice
Return
30-Jul-04 34.40
2-Aug-04 33.54 -2.53%
Return statistics
1-Sep-04 34.64 3.23% Average monthly return 0.18% <-- =AVERAGE(C4:C45)
1-Oct-04 36.38 4.90% Standard deviation of monthly return 3.31% <-- =STDEVP(C4:C45)
1-Nov-04 38.57 5.85%
1-Dec-04 39.73 2.96% Annualized mean return 2.17% <-- =12*F5
3-Jan-05 37.22 -6.53% Annualized sigma 11.48% <-- =F6*SQRT(12)
1-Feb-05 37.05 -0.46%
1-Mar-05 36.40 -1.77%
1-Apr-05 34.82 -4.44%
2-May-05 37.90 8.48%
1-Jun-05 36.64 -3.38%
19-Jul-06 36.62 1.29%
20-Jul-06 36.08 -1.49%
21-Jul-06 35.70 -1.06%
24-Jul-06 36.41 1.97%
25-Jul-06 36.62 0.58%
26-Jul-06 36.59 -0.08%
27-Jul-06 36.35 -0.66%
28-Jul-06 37.11 2.07%
QQQQ HISTORICAL PRICES, MONTHLY DATA
and resulting statistics
19.4.2 The Implied Volatility
The implied volatility ignores history; instead it determines the option
σ based on actual option prices. Whereas the historical volatility is a
backward-looking volatility, the implied volatility is a forward-looking
estimate.
3
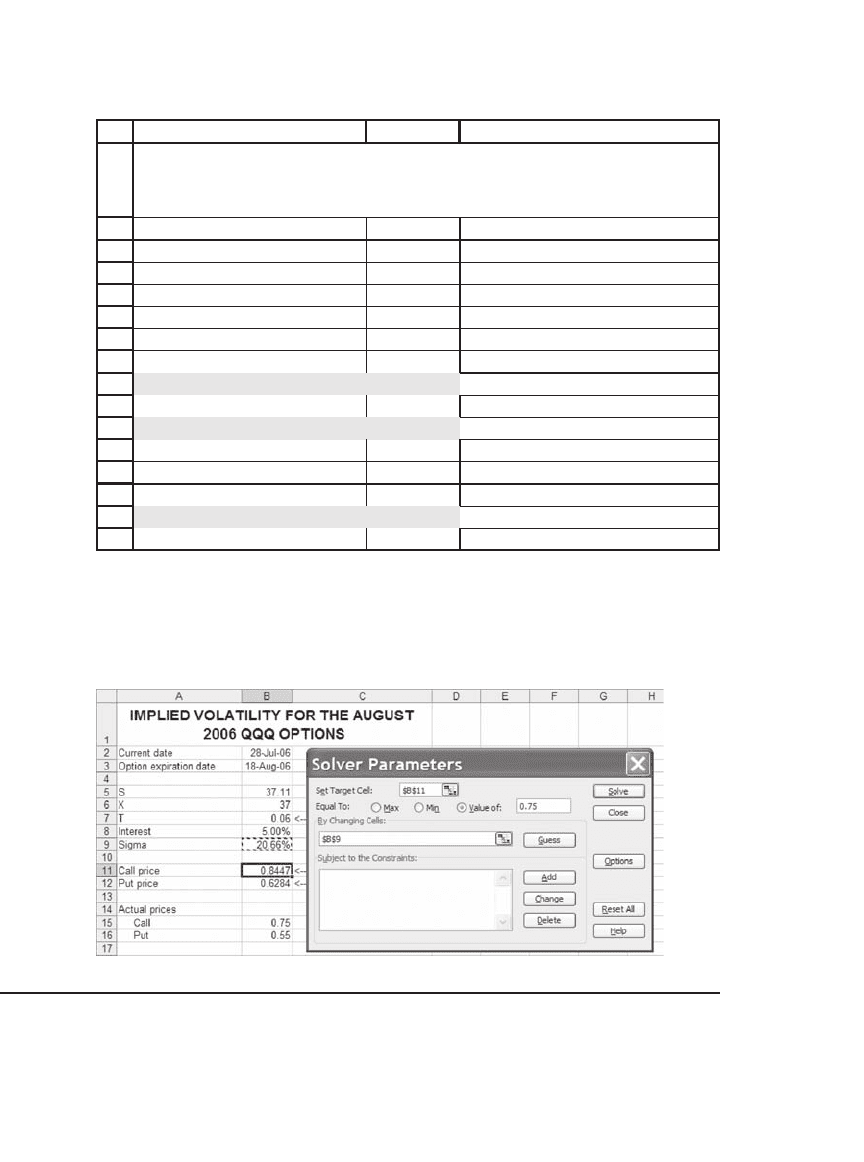
To estimate the implied volatility for the August 2006 QQQQ calls, we
solve the Black-Scholes formula for the sigma that gives the current
market price:
3. The nomenclature “forward-looking” versus “backward-looking” makes it sound as if
the implied volatility is always better than the historical. This is, of course, not the
intention.
517 The Black-Scholes Model
The implied volatility is 17.96 percent. This exactly gives the market
call price of $0.75 (cell B15) and almost gives the market put price of
$0.55 (cell B16). We solved the problem by using Solver:
1
2
3
4
5
6
7
8
9
10
11
13
12
14
15
16
AB C
Current date 28-Jul-06
Option expiration date 18-Aug-06
S 37.11
3X7
T 0.06 <-- =(B3-B2)/365
Int
Im
Put price 0.5337 <-- =BSPut(B5,B6,B7,B8,B9)
Actual prices
Put
IMPLIED VOLATILITY FOR THE
AUGUST 2006 QQQQ OPTIONS
erest 5.00%
plied volatility,
σ
17.96%
Call price 0.7500 <-- =BSCall(B5,B6,B7,B8,B9)
Call 0.75
0.55
19.5 A VBA Function to Find the Implied Variance
We want to design a Visual Basic for Applications function that com-
putes the implied volatility. To do so, we fi rst note that the option price
