Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

478 Chapter 17

As is usual for an American option, at each node of the tree we consider

whether the option is worth more whether exercised or whether held.

But note that in this picture, the exercise price varies with the date, so

that the exercise price at date 3 is E5, that of date 2 is E4, and that of

date 1 is E3. As you can see in cell B28, the value of the American call

option is 8.368.

17.10 Summary

The binomial model is intuitive and easy to implement. As a widespread

alternative to Black-Scholes pricing, the model can easily be put into a

spreadsheet and programmed in VBA. This chapter has explored both

the basic uses of the binomial model and its implementation to price

American and other nonstandard options. A section on employee stock

options has shown how to implement the Hull and White (2004) model

for valuing these options. Throughout, we have laid special stress on the

role of state prices in implementing the model.

Exercises

1. A stock selling for $25 today will, in one year, be worth either $35 or $20. If the

interest rate is 8 percent, what is the value today of a one-year call option on the

stock with exercise price $30? Use the simultaneous equation approach of section

17.2 to price the option.

2. In exercise 1, compute the state prices q

and q

, and use these prices to calculate

the value today of a one-year put option on the stock with exercise price $30. Show

that put-call parity holds: That is, using your answer from this problem and the previ-

ous problem, show that

Call price Stock price today Put price.+

3. In a binomial model, a call option and a put option are both written on the same

stock. The exercise price of the call option is 30, and the exercise price of the put

option is 40. The call option’s payoffs are 0 and 5, and the put option’s payoffs are

20 and 5. The price of the call is 2.25 and the price of the put is 12.25.

a. What is the riskless interest rate? Assume that the basic period is one year.

b. What is the price of the stock today?

4. All reliable analysts agree that a share of ABC Corporation, selling today for $50,

will be priced at either $65 or $45 one year from now. They further agree that the

probabilities of these events are 0.6 and 0.4, respectively. The market risk-free rate

is 6 percent. What is the value of a call option on ABC whose exercise price is $50

and that matures in one year?

479 The Binomial Option-Pricing Model

5. A stock is currently selling for $60. The price of the stock at the end of the year is

expected either to increase by 25 percent or to decrease by 20 percent. The riskless

interest rate is 5 percent. Calculate the price of a European put on the stock with

exercise price $55. Use the binomial option-pricing model.

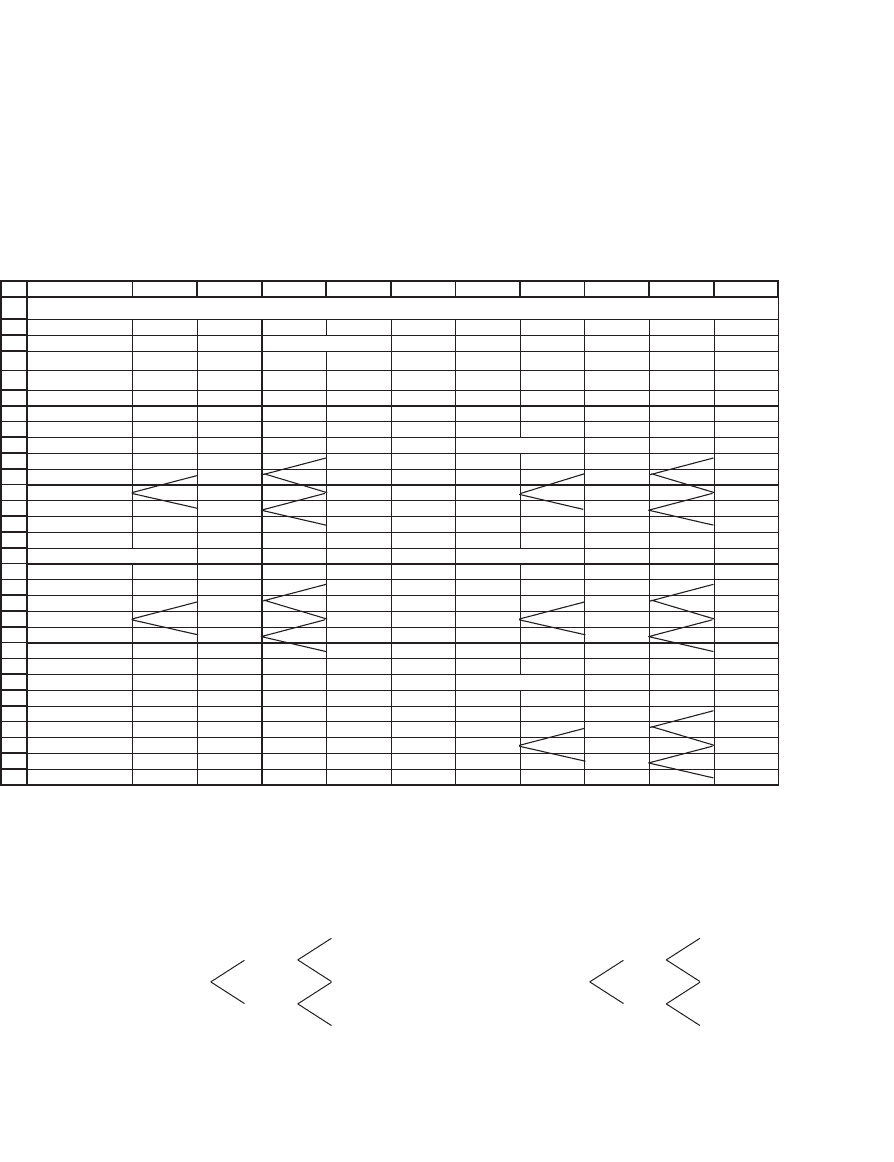
6. Fill in all the cells labeled ??? in the following spreadsheet. Why is there no addi-

tional pricing tree for an American call option?

ABCDEFGHIJK

Up, U 1.35

Down, D 0.95 state prices

Initial stock price 40

Interest rate, R 1.25

Exercise price 40

ecirp dnoBecirp kcotS

???

??????

???104

??????

???

noitpo tup naeporuEnoitpo llac naeporuE

??????

????????????

??????

American put option

???

THREE-DATE BINOMIAL OPTION PRICING

7. Consider the following two-period binomial model, in which the annual interest rate

is 9 percent and in which the stock price goes up by 15 percent per period or down

by 10 percent:

Stock price Bond price

66.1250

1.1881

57.50

1.09

51.7500

1.1881

45.00

1.09

40.5000

1.1881

a. Price a European call on the stock with exercise price 60.

b. Price a European put on the stock with exercise price 60.

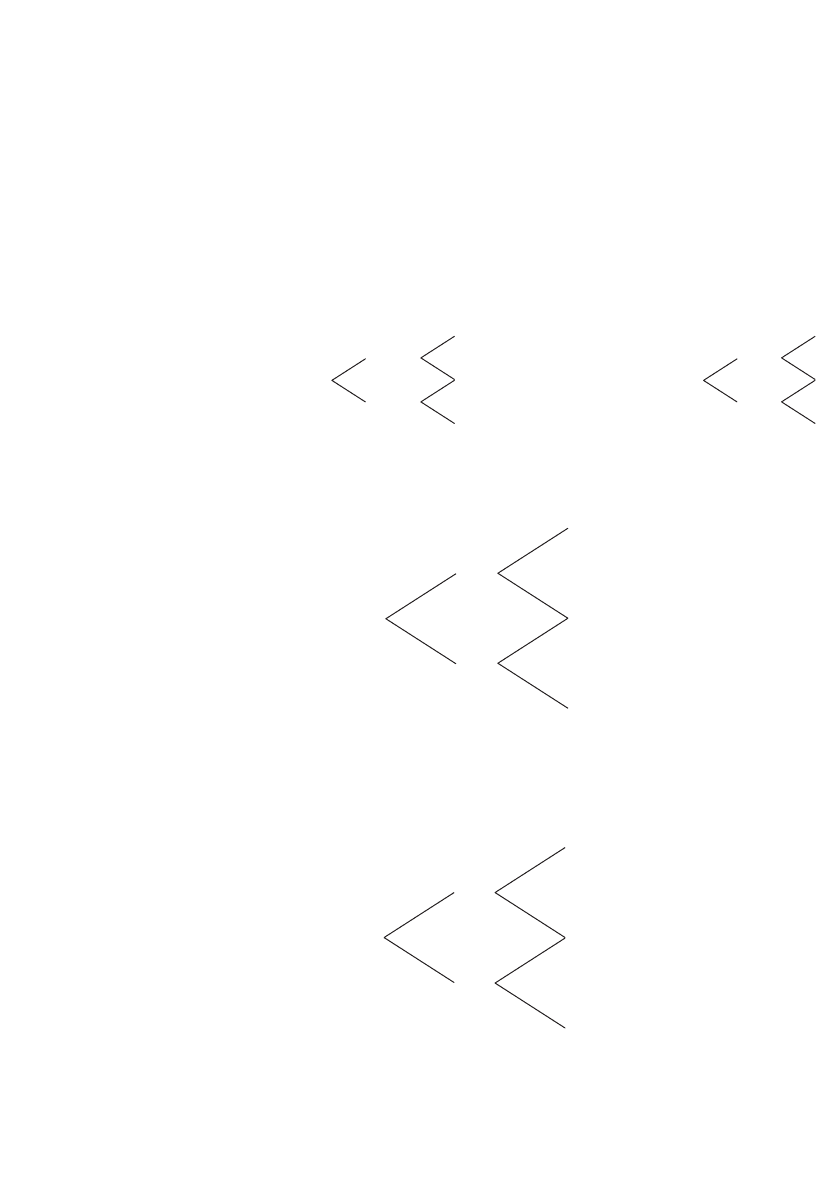
480 Chapter 17

c. Price an American call on the stock with exercise price 60.

d. Price an American put on the stock with exercise price 60.

8. Consider the following three-date binomial model:

•

In each period the stock price either goes up by 30 percent or decreases by

10 percent.

•

The one-period interest rate is 25 percent.

Stock price Bond price

50.70

1.5625

39.00 1.25

35.10

1 1.5625

27.00

1.25

24.30 1.5625

a. Consider a European call with X = 30 and T = 2. Fill in the blanks in the tree:

Call option price

???

b. Price a European put with X = 30 and T = 2.

c. Now consider an American put with X = 30 and T = 2. Fill in the blanks in the

tree:

American put option price

???

9. A prominent securities ﬁ rm recently introduced a new ﬁ nancial product. This

product, called the Best of Both Worlds (BOBOW for short), costs $10. It matures

in ﬁ ve years, at which point it repays the investor the $10 cost plus 120 percent of

any positive return in the S&P 500 index. There are no payments before maturity.

481 The Binomial Option-Pricing Model

For example, if the S&P 500 is currently at 1500, and if it is at 1800 in ﬁ ve years,

a BOBOW owner will receive back $12.40 = $10

[1 + 1.2

(1800/1500 − 1)]. If the

S&P is at or below 1500 in ﬁ ve years, the BOBOW owner will receive back $10.

Suppose that the annual interest rate on a ﬁ ve-year, continuously compounded,

pure-discount bond is 6 percent. Suppose further that the S&P 500 is currently at

1500 and that you believe that in ﬁ ve years it will be at either 2500 or 1200. Use the

binomial option-pricing model to show that BOBOWs are underpriced.

10. This problem is a continuation of the discussion of section 17.6.1. Show that as

n → ∞, the binomial European put price converges to the Black-Scholes put price.

(Note that, as part of the spreadsheet fm3_chapter17.xls, we have included a func-

tion called BSPut that computes the Black-Scholes put price.)

11. Here’s an advanced version of exercise 10. Consider an alternative parameterization

of the binomial:

ΔΔ

tTn Re

rtt

−

∗−

−+

(

Down

Up Down)

Down

/2)

σσ

−−−

=−

σσ

/2)ΔΔtt

Construct binomial European call and put option-pricing functions in VBA for this

parameterization, and show that they also converge to the Black-Scholes formula.

(The message here is that the parameterization of the binomial σ is not unique.)

12. A call option is written on a stock whose current price is $50. The option has matu-

rity of three years, and during this time the annual stock price is expected to increase

by 25 percent or to decrease by 10 percent. The annual interest rate is constant at

6 percent. The option is exercisable at date 1 at a price of $55, at date 2 for a price

of $60, and at date 3 for a price of $65. What is its value today? Will you ever exercise

the option early?

13. Reconsider exercise 12. Show that if the date-1 exercise price is X, the date-2 exer-

cise price is X

(1 + r), and the date-3 exercise price is X

(1 + r)

, you will not

exercise the option early.

14. An investment bank is offering a security linked to the price two years from today

of Bisco stock, which is currently at $3 per share. Denote Bisco’s stock price in two

periods by S

. The security being offered pays off Max(S

− 40,0). You estimate that

in each of the next two periods, Bisco stock will increase by either 50 percent or

decrease by 20 percent. The annual interest rate is 8 percent. Price the security.

11. It can also be shown that this property holds if the exercise prices grow more slowly

than the interest rate. Thus for the problem considered in section 17.7, there will be

early exercise of the American call only when the exercise prices grow at a rate faster

than the interest rate.

The Lognormal Distribution

18.1 Overview

In the previous chapter we discussed the pricing of options using the

binomial option-pricing model. The binomial model—besides being an

attractive and intuitive way to price options and other derivative securi-

ties—also has a deeper message for derivative asset pricing: It shows us

that, given some assumptions about the uncertainty governing the stock

price and given a risk-free interest rate, we can price options and other

assets whose prices are dependent on the price of an underlying stock.

A problem with the binomial option-pricing approach is that we were

not able to give simple formulas for the pricing of options. The pricing

approach developed in the previous chapter is computational, not

analytic. In order to develop a formula for the pricing of options (such

as the Black-Scholes formula, discussed in Chapter 19), we need to make

some assumptions about the statistical properties of the underlying stock

price.

A central assumption of the Black-Scholes (BS) pricing model is

that stock prices are distributed lognormally. An alternative statement

of this assumption is that stock returns are distributed normally. In

this chapter we attempt to give this assumption enough content so

that you will be happy using it. Our method is as follows: We shall

not, in this book, prove the Black-Scholes option-pricing formula. Instead,

we shall try to convince you in this chapter that the basic assumption

made by the BS model with regard to stock prices—the lognormality of

stock prices—is reasonable. If we can convince you that it is, then we will

leave the technical details of the BS proof to other, more advanced,

texts.

The structure of this chapter is as follows:

•

We start with a discussion of what constitutes “reasonable” assump-

tions about stock prices.

•

We then discuss why the lognormal distribution is a reasonable distri-

bution for stock prices.

•

Next, we show how to simulate lognormal price paths.

•

Finally, we show you how to derive the parameters of the lognormal

distribution—the mean and standard deviation of the stock returns—

from historical stock price data.

484 Chapter 18

18.2 What Do Stock Prices Look Like?

What are reasonable assumptions about the way stock prices behave

over time? Clearly the price of a stock (or any other risky ﬁ nancial asset)

is uncertain. What is its distribution? This is a perplexing question. One

way to answer this question is to ask what are reasonable statistical

properties of a stock price. Here are ﬁ ve reasonable properties:

1. The stock price is uncertain. Given the price today, we do not know

the price tomorrow.

2. Changes in the stock’s price are continuous. Over short periods of

time, changes in a stock’s price are very small, and the change goes to

zero as the time span goes to zero.

3. The stock price is never zero. This property means that we exclude the

stocks of “dead” companies.

4. The average return from holding a stock tends to increase over time.

Notice the word “tends”: We do not know that holding a stock for a

longer time will lead to a higher return; however, we expect that holding

a risky asset over a longer term will lead to a higher average return.

5. The uncertainty associated with the return from holding a stock also

tends to increase the longer the stock is held. Thus, given the stock’s price

today, the variance of the stock price tomorrow is small; however, the

price variance in one month is larger, and the variance in one year is

larger still.

18.2.1 Reasonable Stock Properties and Stock Price Paths

One way of viewing these ﬁ ve “reasonable properties” of stock prices is

to think about price paths. A stock price path is a graph of a stock price

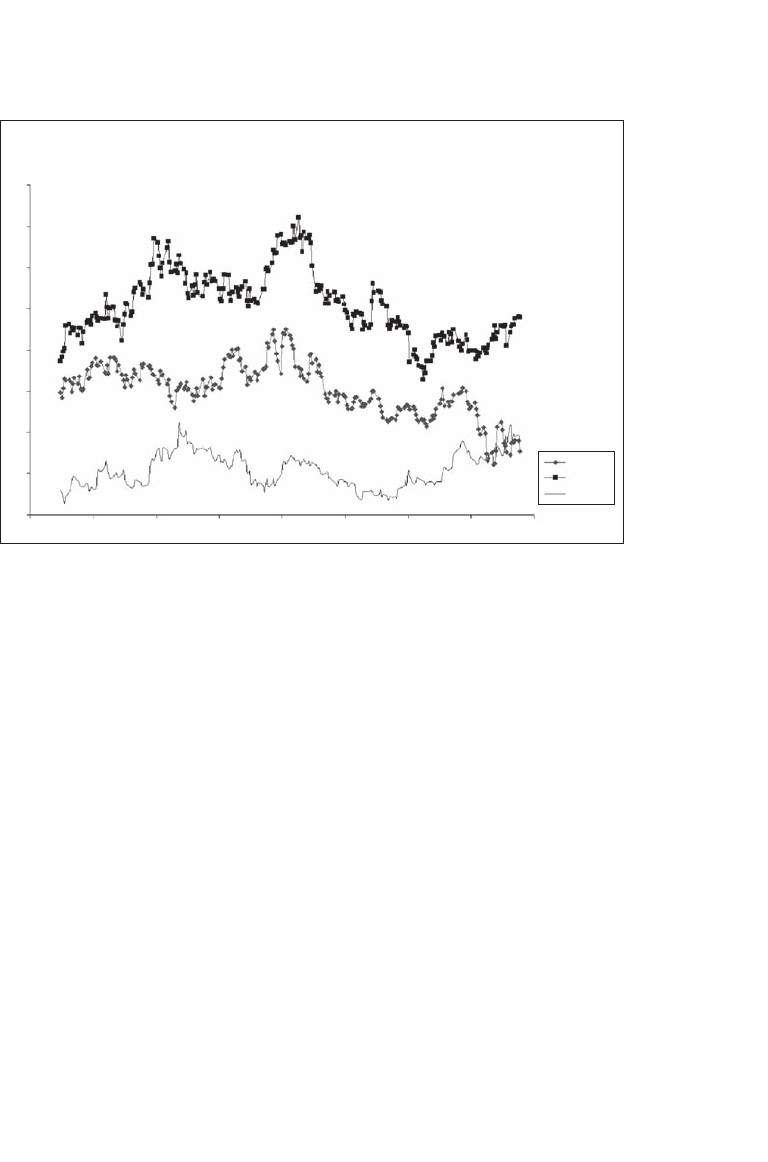
over a period of time. Here, for example, is the price path of several

actual stocks:

1. If you have watched stock prices, you know that continuity is usually not a bad assump-

tion. Sometimes, however, it can be disastrous (look at the way stock market prices

behaved in October 1987, for a dramatic example of price discontinuities). It is possible

to build a stock-price model that assumes that prices are usually continuous but have

occasional (and random) jumps. See Cox and Ross (1976), Merton (1976), and Jarrow

and Rudd (1983).

485 The Lognormal Distribution

If we simulated stock price paths (something we will do using the log-

normal model later on in this chapter), how would we expect them to

look? Our ﬁ ve properties imply that we would expect

1. Wiggly lines.

2. Lines that are continuous (solid), with no jumps.

3. Lines that are always positive and never cross zero, no matter how

low they get.

4. That at a given point in time, the average over all plausible lines is

greater than the initial price of the stock. The farther out we go, the

higher this average becomes.

5. That the standard deviation over all plausible lines is greater the

farther out we go.

Here’s another way of thinking about stock prices. Suppose we take

the daily returns on the Standard & Poor’s 500 index (we only show the

start of the data):

2-Oct-98

21-Nov-98 10-Jan-99 1-Mar-99 20-Apr-99 9-Jun-99 29-Jul-99 17-Sep-99 6-Nov-99

Abbott

Daily Prices for Three Stocks

Ford

Kellogg

486 Chapter 18

If we graph these returns over any given period, we get a mess of dots

that is difﬁ cult to interpret:

ABC D

Date Price Return

3-Jan-50 16.66

4-Jan-50 16.85 1.13% <-- =LN(B4/B3)

5-Jan-50 16.93 0.47%

6-Jan-50 16.98 0.29%

9-Jan-50 17.08 0.59%

10-Jan-50 17.03 -0.29%

11-Jan-50 17.09 0.35%

12-Jan-50 16.76 -1.95%

13-Jan-50 16.67 -0.54%

16-Jan-50 16.72 0.30%

17-Jan-50 16.86 0.83%

18-Jan-50 16.85 -0.06%

19-Jan-50 16.87 0.12%

20-Jan-50 16.9 0.18%

23-Jan-50 16.92 0.12%

24-Jan-50 16.86 -0.36%

25-Jan-50 16.74 -0.71%

26-Jan-50 16.73 -0.06%

27-Jan-50 16.82 0.54%

30-Jan-50 17.02 1.18%

31-Jan-50 17.05 0.18%

1-Feb-50 17.05 0.00%

2-Feb-50 17.23 1.05%

3-Feb-50 17.29 0.35%

S&P 500 DAILY PRICES

1950-2006

487 The Lognormal Distribution

Three extreme returns for the S&P 500 occurred on the day of the

1987 stock market crash (19 October 1987, a decline of 22.9 percent in

the S&P) and in the two days following (increases of 5.20 percent and

8.71 percent on 20 and 21 October 1987, respectively). The decline of 19

October and the increase on 21 October are marked on the chart with

large diamonds.

This smear of dots on a graph is difﬁ cult to interpret. Excel can help

us make some sense of the data:

S&P 500 Daily Returns, 1950–2005

-23

Daily return (%)

-21

-19

-17

-15

-13

-11

-9

-7

-5

-3

-1

Jan-

29-

Sep-

26-

Jun-

22-

Mar-

16-

Dec-

12-

Sep-

Jun-

Mar-

29-

Nov-

25-

Aug-

21-

May-

15-

Feb-

11-

Nov-

Aug-

May-

28-

Jan-

24-

Oct-

20-

Jul-

16-

Apr-

10-

Jan-

Oct-

ABC D E F G H

Date Price Return

3-Jan-50 16.66

4-Jan-50 16.85 1.13% <-- =LN(B4/B3) Count 14,094 <-- =COUNT(C4:C14097)

5-Jan-50 16.93 0.47%

6-Jan-50 16.98 0.29% Maximum daily return 8.71% <-- =MAX(C4:C14097)

9-Jan-50 17.08 0.59% Minimum daily return -22.90% <-- =MIN(C4:C14097)

10-Jan-50 17.03 -0.29%

11-Jan-50 17.09 0.35%

Number of returns between

-1% and +1%

11,436

<-- =SUMPRODUCT((C4:C14097>-

1%)*(C4:C14097<1%),(C4:C14097>-

1%)*(C4:C14097<1%))

12-Jan-50 16.76 -1.95%

13-Jan-50 16.67 -0.54% Daily mean return 0.0309% <-- =AVERAGE(C4:C14097)

16-Jan-50 16.72 0.30% Daily standard deviation 0.899% <-- =STDEV(C4:C14097)

17-Jan-50 16.86 0.83%

18-Jan-50 16.85 -0.06% Annual return 7.78% <-- =G11*252

19-Jan-50 16.87 0.12% Annual standard deviation 14.27% <-- =G12*SQRT(252)

20-Jan-50 16.9 0.18%

S&P 500 DAILY PRICES AND RETURNS, 1950-2005

Some distributional details