Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

468 Chapter 17

In this example, the employee stock option is given when the stock

price is $50. The ESO has exercise price X = $50. The option has a 10-

year maturity and a three-year vesting period. The interest rate is 5

percent annually, and the stock pays an annual dividend of 2.5 percent

of its stock value. The rate at which employees leave the company is 10

percent per year. The model assumes that after the vesting period, the

employee will choose to exercise his option if the stock price is three or

more times the option’s exercise price.

The binomial model with which

the computations in cell B13 were done divides each year into 50

subdivisions.

Given these assumptions, the employee stock option is valued at $13.56

(cell B13). A comparable Black-Scholes option on a dividend-paying

stock would be valued at $19.18.

17.8.1 The ESO Valuation and FASB 123

The American Financial Accounting Standards Board (FASB) and the

International Accounting Standards Board (IASB) agree that executive

stock options should be priced using a model of the type explored here

and that the value of options awarded should be accounted for in a ﬁ rm’s

net income. If, for example, a ﬁ rm had issued 1 million options of the

8. Research cited by Hull and White (2004) shows that the average stock-price-to-

exercise-price ratio at which ESO owners exercise their options is between 2.2 and

2.8.

9. We’re getting way ahead of ourselves here! The adaptation of Black-Scholes for

dividend-paying stock is given in section 19.6.

469 The Binomial Option-Pricing Model

type that appears in the previous spreadsheet, we would value these

options at $13,564,600.

17.8.2 The VBA Code for the ESO Model

In this subsection we give the VBA code for this model. A short discus-

sion follows the code.

Function ESO(Stock As Double, X As Double, T

As Double, Vest As Double, _

Interest As Double, Sigma As Double, _

Divrate As Double, _

Exitrate As Double, Multiple As Double, _

n As Single)

Dim Up As Double, Down As Double, R As _

Double, Div As Double, _

piUp As Double, piDown As Double, Delta _

As Double, _

i As Integer, j As Integer

ReDim Opt(T * n, T * n)

ReDim S(T * n, T * n)

Up = Exp(Sigma * Sqr(1 / n))

Down = Exp(-Sigma * Sqr(1 / n))

R = Exp(Interest / n)

Div = Exp(-Divrate / n)

piUp = (R * Div - Down) / (Up - Down)

‘Risk-neutral up probability

piDown = (Up - R * Div) / (Up - Down)

‘Risk-neutral down probability

‘Deﬁ ning the stock price

For i = 0 To T * n

For j = 0 To i ‘ j is the number of

‘Up steps

S(i, j) = Stock * Up ^ j * Down ^ _

(i - j)

Next j

Next i

470 Chapter 17

17.8.3 Explaining the VBA Code

The VBA code has several parts. The ﬁ rst part deﬁ nes the variables,

adjusting the Up, Down, and 1 + interest R for the n divisions of each

year. Having made this adjustment, the code deﬁ nes the risk-neutral

probabilities π

and π

Down

‘Deﬁ ning the option value on the last

‘nodes of tree

For i = 0 To T * n

Opt(T * n, i) = Application.Max(S(T _

* n, i) - X, 0)

Next i

‘Early exercise when stock price >

‘multiple * exercise after vesting

For i = T * n - 1 To 0 Step -1

For j = 0 To i

If i > Vest * n And S(i, j) >= Multiple _

* X Then _

Opt(i, j) = Application.Max _

(S(i, j) - X, 0)

If i > Vest * n And S(i, j) < Multiple * _

X Then _

Opt(i, j) = ((1 - Exitrate / n) * _

(piUp * Opt(i + 1, j + 1) + _

piDown * Opt(i + 1, j)) / R + _

Exitrate / n * _

Application.Max(S(i, j) - X, 0))

If i <= Vest * n Then Opt(i, j) = _

(1 - Exitrate / n) * _

(piUp * Opt(i + 1, j + 1) + piDown * _

Opt(i + 1, j)) / R

Next j

Next i

ESO = Opt(0, 0)

End Function

10. This subsection is tedious and can be skipped. But take a look at the next subsection,

where we use Data|Table to do sensitivity analysis.

471 The Binomial Option-Pricing Model

The stock price is deﬁ ned as an array S(i, j), where i deﬁ nes the periods,

i = 0, 1, . . . , T

n, and j deﬁ nes the number of Up steps at each period,

j = 0, 1, . . . , i. The next part of the code deﬁ nes the stock price

Up = Exp(Sigma * Sqr(1 / n))

Down = Exp(-Sigma * Sqr(1 / n))

R = Exp(Interest / n)

Div = Exp(-Divrate / n)

piUp = (R * Div - Down) / (Up - Down)

‘Risk-neutral up probability

piDown = (Up - R * Div) / (Up - Down)

‘Risk-neutral down probability

‘Deﬁ ning the stock price

For i = 0 To T * n

For j = 0 To i ‘ j is the number of

Up steps

S(i, j) = Stock * Up ^ j * Down ^ _

(i - j)

Next j

Next i

The option values are deﬁ ned in the next piece of code, which is the

heart of our employee-stock-option function. Option value is deﬁ ned as

an array opt(i, j):

‘Deﬁ ning the option value on the last nodes of

‘tree

For i = 0 To T * n

Opt(T * n, i) = Application.Max(S(T * n, i) _

- X, 0)

Next i

‘Early exercise when stock price > multiple *

‘exercise after vesting

For i = T * n - 1 To 0 Step -1

For j = 0 To i

472 Chapter 17

Here’s what this piece of code says:

opt ,

max , , 0] terminal nodes

max , , 0] afte

()

[( )

ST n j X

Sij X

∗−

− rr vesting, ,

Exitrate/

opt , op

Up Down

Sij m X

()

≥∗

−∗

+++

ππ

tt,

after vesting, ,

Exitrate/ Max

()

[(,) ,

Sij m X

nSijX

<∗

+∗ −

11 1

]

()

() )

−∗

+++ +

Exitrate/

opt , opt( ,

before ve

Up Down

ij ij

ππ

ssting

⎧

⎨

⎪

⎩

⎪

At the terminal nodes, we simply exercise the option. Before the ter-

minal nodes and after vesting, we check to see whether the stock price

is greater than the desired multiple m of the exercise price. If it is, we

exercise the option. If S(i, j) < m

X the ESO’s payoff depends on

whether the employee exits the ﬁ rm or not. With a probability (1 − Exit-

rate/n) the employee does not exit the ﬁ rm, in which case the option

payoff is the discounted expected next-period payoff:

()

)()

11 1

−∗

+++ +

Exitrate/

opt( , opt ,

Up Down

ij ij

ππ

If i > Vest * n And S(i, j) >= Multiple * X

Then _

Opt(i, j) = Application.Max(S(i, j) - X, 0)

If i > Vest * n And S(i, j) < Multiple * X

Then _

Opt(i, j) = ((1 - Exitrate / n) * (piUp * _

Opt(i + 1, j + 1) + _

piDown * Opt(i + 1, j)) / R + Exitrate / n _

* _

Application.Max(S(i, j) - X, 0))

If i <= Vest * n Then Opt(i, j) = (1 - _

Exitrate / n) * _

(piUp * Opt(i + 1, j + 1) + piDown * Opt(i _

+ 1, j)) / R

Next j

Next i

473 The Binomial Option-Pricing Model

However, if the employee exits the ﬁ rm and the vesting period has

passed, he will try to see if he can exercise the option, giving the expected

payoff

Exitrate/ max[ , , 0]nSijX∗−()

Finally, before vesting, the ESO is simply worth the expected payoff,

discounted (by the risk-neutral probabilities), of the next-period

values:

()

() )

11 1

−∗

+++ +

Exitrate/

opt , opt( ,

Up Down

ij tj

ππ

The ﬁ nal step in the code is to deﬁ ne the value of the function ESO:

ESO = opt(0, 0).

17.8.4 Some Sensitivity Analysis

We can use data tables to perform sensitivity analysis on our ESO

function.

AB DCEF

X 50 Option exercise price

T 10.0000 Time to option exercise (in years)

Vesting period (years) 3.00

Interest 5.00% Annual interest rate

Sigma 35% Riskiness of stock

Stock dividend rate 2.50% Annual dividend rate on stock

Exit rate, e 10.00%

Option exercise multiple, m 3.00

n 25 Number of subdivisions of one year

Employee stock option value 13.5275 <-- =ESO(B2,B3,B4,B5,B6,B7,B8,B9,B10,B11)

Black-Scholes call 19.1842 <-- =BSCall(B2*EXP(-B8*B4),B3,B4,B6,B7)

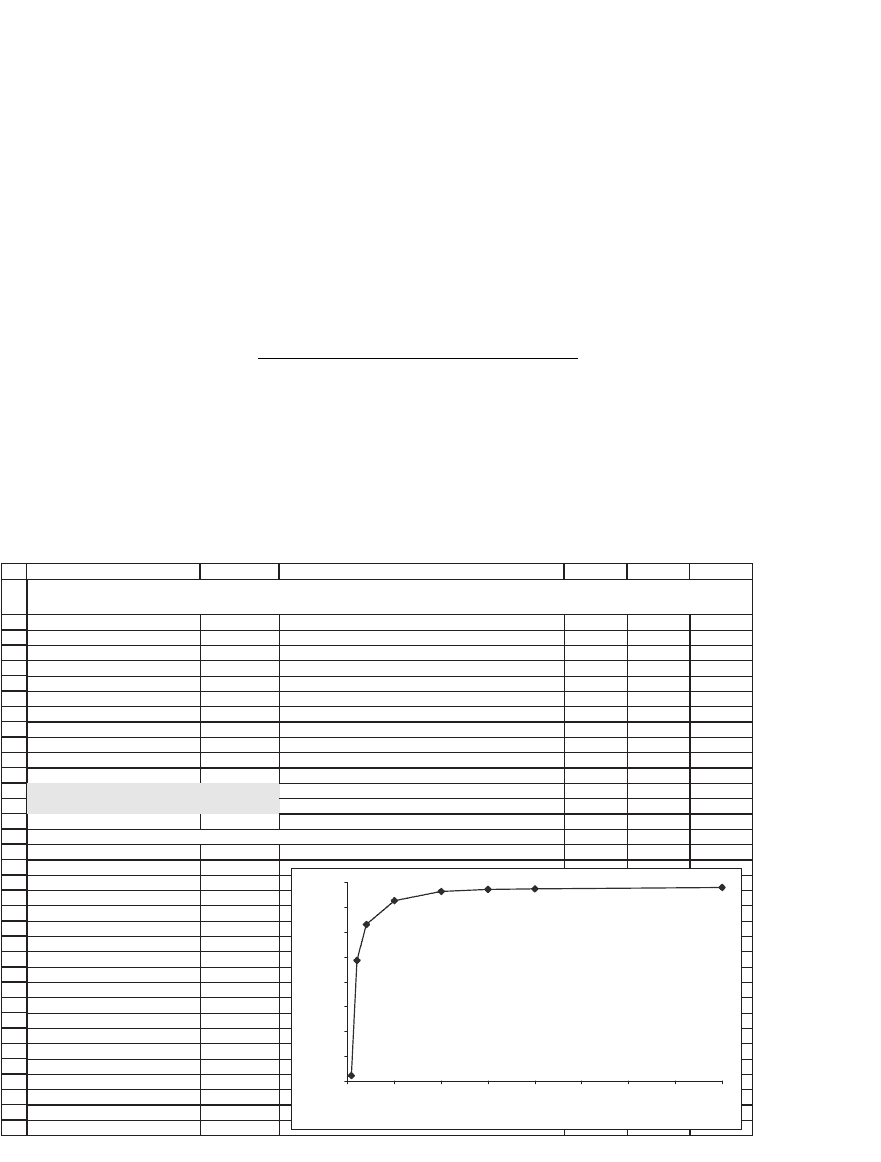
Sensitivity of ESO value to number of subdivisions n

n 13.5275 <-- =B13, data table header

2 12.8213

5 13.2870

10 13.4312

25 13.5275

50 13.5646

75 13.5733

100 13.5753

200 13.5810

ESO FUNCTION SENSITIVITY TO NUMBER OF SUBDIVISIONS n OF ONE YEAR

50 Current stock price

12.80

12.90

13.00

13.10

13.20

13.30

13.40

13.50

13.60

0 25 50 75 100 125 150 175 200

Subdivisions, n

ESO

474 Chapter 17

The graph gives ample evidence that n = 25 or 50 does well enough

for valuing ESOs. Since larger values of n become time-consuming, we

recommend lower numbers.

In the next graph we show the sensitivity of the ESO value to the

employee exit rate e, the rate at which employees leave the ﬁ rm each

year:

DCBA E

S 50 Current stock price

X 50 Option exercise price

T 10.0000 Time to option exercise (in years)

Vesting period (years) 3.00

Interest 5.00% Annual interest rate

Sigma 35% Riskiness of stock

Stock dividend rate 2.50% Annual dividend rate on stock

Exit rate, e 10.00%

Option exercise multiple, m 3.00

n 50 Number of subdivisions of one year

Employee stock option value 13.5646 <-- =ESO(B2,B3,B4,B5,B6,B7,B8,B9,B10,B11)

Black-Scholes call 19.1842 <-- =BSCall(B2*EXP(-B8*B4),B3,B4,B6,B7)

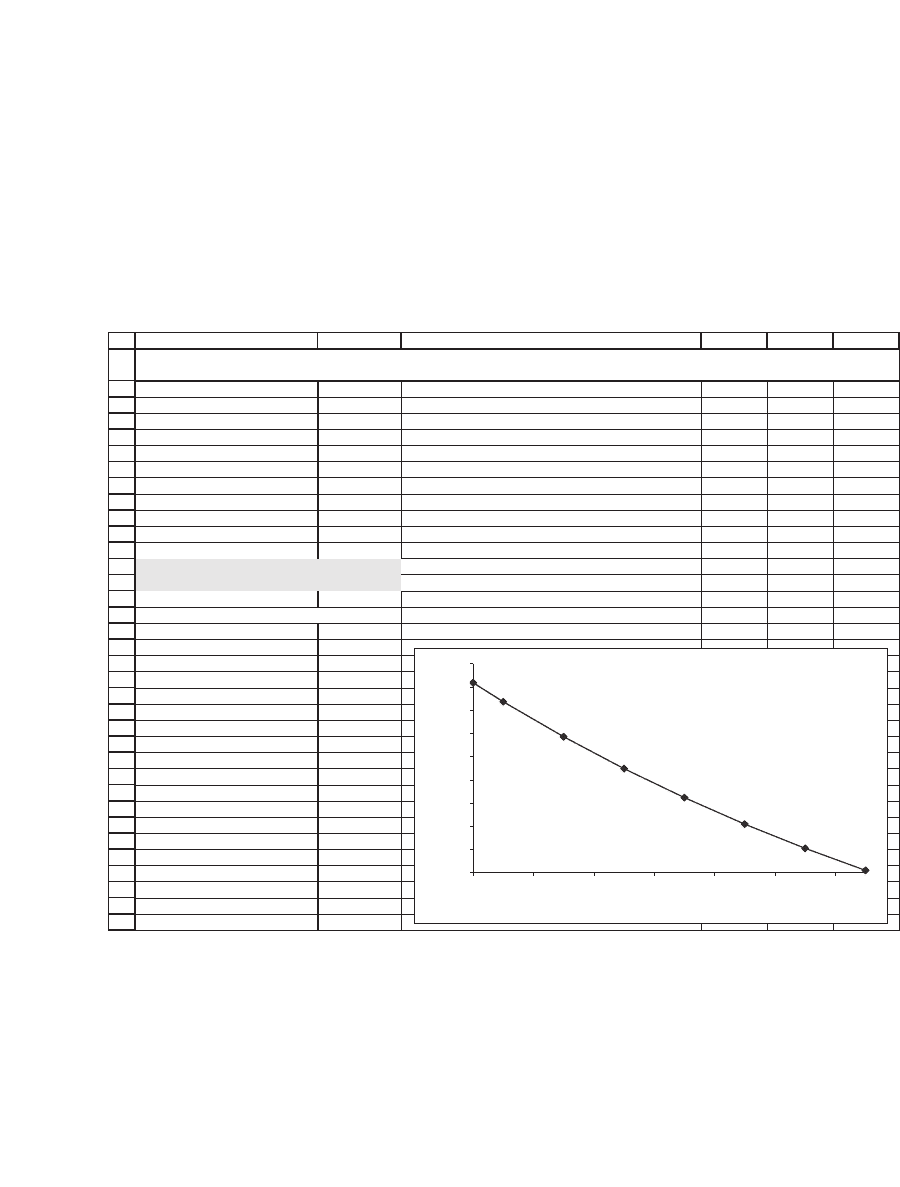
Sensitivity of ESO value to exit rate e

Exit rate, e 13.5646 <-- =B13, data table header

0% 20.1732

1% 19.3621

3% 17.8536

5% 16.4828

7% 15.2347

9% 14.0963

11% 13.0561

13% 12.1039

ESO FUNCTION SENSITIVITY TO EMPLOYEE EXIT RATE e

12.00

13.00

14.00

15.00

16.00

17.00

18.00

19.00

20.00

21.00

024681012

Exit rate, e (%)

ESO

The exit rate has a major effect on the value of the ESO: The higher

the turnover of employees, the lower the value of the employee stock

options. In terms of FASB 123 valuation, the exit rate e is an important

valuation factor.

Finally we do a sensitivity analysis of the ESO value on the exit mul-

tiple m. Recall that the Hull-White model assumes that an employee

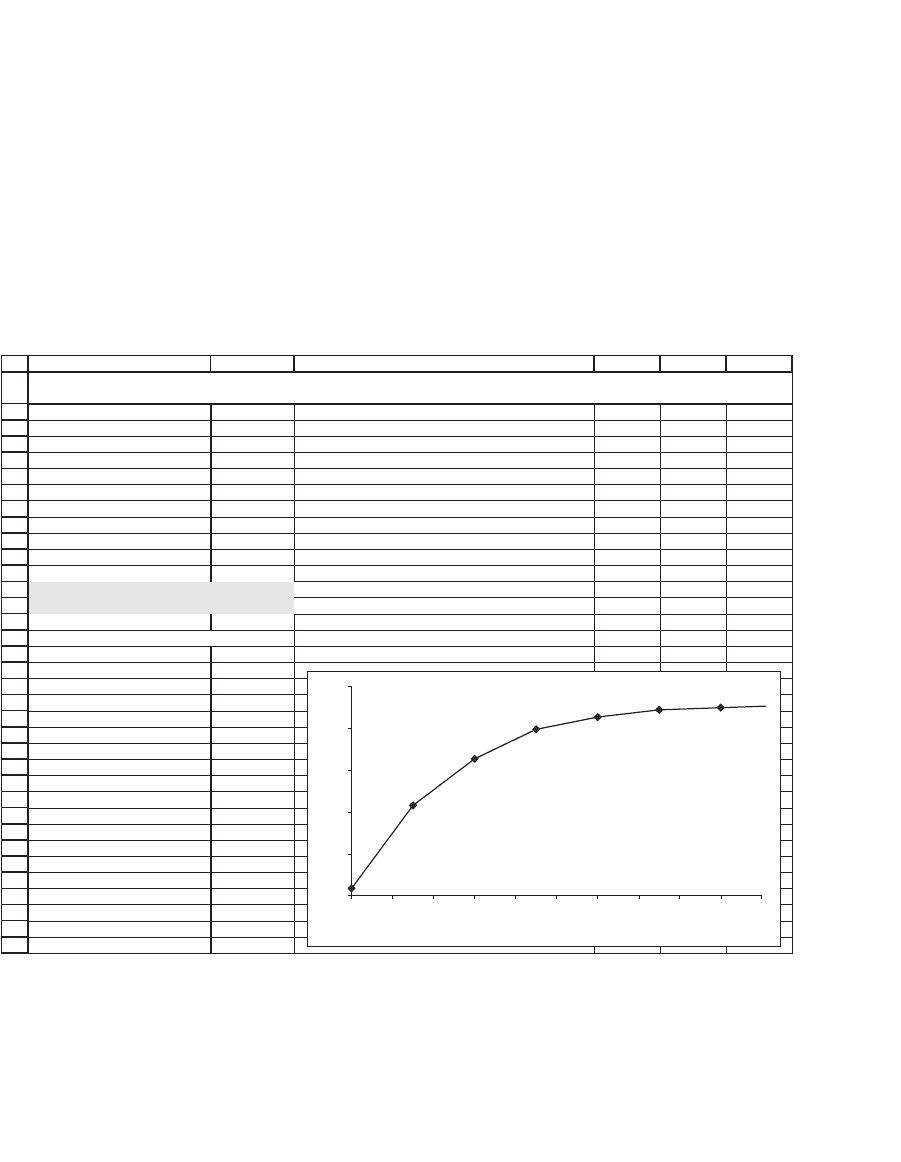
475 The Binomial Option-Pricing Model

holding an ESO exercises her option when the stock price is a multiple

m of the option exercise price X. Basically this assumption locks the

employee into a suboptimal strategy, since in general call options should

be held to maturity (though note that in this case the option is written

on a stock that pays a dividend, which may in some cases make early

exercise optimal). In the next example we clearly see the suboptimality

of early ESO exercise: The higher the multiple m, the higher the value

of the ESO.

DCBA E

S 50 Current stock price

X 50 Option exercise price

T 10.0000 Time to option exercise (in years)

Vesting period (years) 3.00

Interest 5.00% Annual interest rate

Sigma 35% Riskiness of stock

Stock dividend rate 2.50% Annual dividend rate on stock

Exit rate, e 10.00%

Option exercise multiple, m 3.00

n 25 Number of subdivisions of one year

Employee stock option value 13.5275 <-- =ESO(B2,B3,B4,B5,B6,B7,B8,B9,B10,B11)

Black-Scholes call 19.1842 <-- =BSCall(B2*EXP(-B8*B4),B3,B4,B6,B7)

Sensitivity of ESO value to multiple m

m 13.5275 <-- =B13, data table header

1.0 9.1758

1.3 11.1610

1.6 12.2760

1.9 12.9793

2.2 13.2735

2.5 13.4467

2.8 13.4985

3.1 13.5423

ESO FUNCTION SENSITIVITY TO EMPLOYEE EXIT RATE m

1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8 3.0

Multiple m

ESO

476 Chapter 17

17.8.5 Last but Not Least

The Hull-White model is a numerical approximation of the ESO option

valuation, but it is not a closed-form formula. A recent paper by Cvitanic´,

Wiener, and Zapatero (2006) gives an analytical derivation of the value

of employee stock options. The formula stretches over 16 pages of type-

script and will not be given here. However, an Excel implementation of

the formula exists and can be downloaded at http://pluto.mscc.huji.ac.il/

~mswiener/research/ESO.htm.

17.9 Using the Binomial Model to Price Nonstandard Options: An Example

The binomial model can also be used to price nonstandard options. Con-

sider the following example: You hold an option to buy a share of a

company. The option allows for early exercise, but the exercise price

varies with the time at which you choose to exercise. For the case we

consider, the option has the following conditions:

•

There are n possible exercise dates only (i.e., the option is only exercis-

able on these dates).

•

Exercise at date t precludes exercise at all dates s > t. However, if you

don’t exercise at date s, you may still exercise at date t > s.

•

The exercise price at date t is X

. In other words, the exercise price can

vary with time.

We want to value this option using a binomial framework. To do so,

we recognize that basically this is just an American option with three

separate exercise prices.

Here’s how we set this problem up in a spreadsheet, using the logic of

the American option valuation described in section 17.5:

477 The Binomial Option-Pricing Model

Most of this spreadsheet follows section 17.5. Cells B15:H21 describe

the stock price over time, which follows a binomial process with the

Up = 1.10 and Down = 0.95 (cells B3 and B4). Where things get interest-

ing is in the valuation:

IHGFEDCBA

Initial stock price 100

Exercise prices

Up 10% Date 1 100

Down -5% Date 2 105

Interest rate 6% Date 3 112

State prices

0.6918 <-- =(B5-B4)/((1+B5)*(B3-B4))

0.2516 <-- =(B3-B5)/((1+B5)*(B3-B4))

Check

1/(q

)

1.06 <-- =1/(B8+B9)

*(1+up)+q

*(1+down)

1 <-- =B8*(1+B3)+B9*(1+B4)

Stock price

133.100

121.000

110.000 114.950

100.000 104.500

95.000 99.275

90.250

85.738

Date 0 Date 1 Date 2 Date 3

Value at each node

21.100 <-- =MAX(H16-E6,0)

16.000

11.583 2.950 <-- =MAX(H18-E6,0)

8.368 2.041

1.412 0.000

0.000

Early exercise?

yes

TIME-DEPENDENT EXERCISE PRICES

=MAX(q

*H25+q

*H27,MAX(F16-E4,0))

=IF(q

*H25+q

*H27>=

MAX(F16-E4,0),"no","yes")

=MAX(q

*F28+q

*F30,MAX(D19-E3,0))

IHGFEDCBA

Date 0 Date 1 Date 2 Date 3

Value at each node

21.100 <-- =MAX(H16-E6,0)

16.000

11.583 2.950 <-- =MAX(H18-E6,0)

8.368 2.041

1.412 0.000

0.000

=MAX(q

*H25+q

*H27,MAX(F16-E4,0))

=MAX(q

*F28+q

*F30,MAX(D19-E3,0))