Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

448 Chapter 17

To drive home the equivalence between state prices and risk-neutral

prices, we close this subsection with a numerical example:

Pricing by state prices

+ q

* X

Pricing by risk-neutral prices

(

* X

)/R

Equivalence of Pricing by State

Prices and Risk-Neutral Prices

Relation of risk-neutral to state prices:

= q

* R,

= q

* R

CBA

Up, U 1.10

Down, D 0.97

Interest rate, R 1.06

Initial stock price, S 50.00

Option exercise price, X 50.00

State prices

0.6531 <-- =(B4-B3)/(B4*(B2-B3))

0.2903 <-- =(B2-B4)/(B4*(B2-B3))

Risk-neutral prices

= q

0.6923 <-- =B9*$B$4

= q

0.3077 <-- =B10*$B$4

Pricing the call and the put using state prices

Call price 3.2656 <-- =B9*MAX(B5*B2-B6,0)+B10*MAX(B5*B3-B6,0)

Put price 0.4354 <-- =B9*MAX(B6-B5*B2,0)+B10*MAX(B6-B5*B3,0)

Pricing the call and the put using risk-neutral prices

Call price 3.2656 <-- =(B13*MAX(B5*B2-B6,0)+B14*MAX(B5*B3-B6,0))/B4

Put price 0.4354 <-- =(B13*MAX(B6-B5*B2,0)+B14*MAX(B6-B5*B3,0))/B4

RISK-NEUTRAL PRICES OR STATE PRICES?

449 The Binomial Option-Pricing Model

17.4 The Multiperiod Binomial Model

The binomial model can easily be extended to more than one period.

Consider, for example, a two-period (three-date) binomial model that

has the following characteristics:

•

In each period the stock price goes up by 10 percent or down by 3

percent from what it was in the previous period. Therefore, U = 1.10, D

= 0.97.

•

In each period the interest rate is 6 percent, so that R = 1.06.

Because U, D, and R are the same in each period,

RU D

−

()

.0 6531 0 2903,

We can now use these state prices to price a call option written on the

stock after two periods. As before, we assume that the stock price is $50

initially and that the call exercise price is X = 50 after two periods. These

assumptions give the following picture:

Stock price Bond price

60.5000 1.1236

55.0000 1.0600

50.0000

53.3500

1.00

1.1236

48.5000 1.0600

47.0450 1.1236

Date 0 Date 1 Date 2

Call option price

10.5000

7.8302

5.7492

3.3500

2.1880

0.0000

How was the call option price of 5.7492 determined? To make this deter-

mination, we go backward, starting at period 2:

At date 2: At the end of two periods the stock price is either $60.50 (cor-

responding to two “up” movements in the price), $53.35 (one “up” and

one “down” movement), or $47.05 (two “down” movements in the price).

450 Chapter 17

Given the exercise price of X = 50, therefore, the terminal option payoff

in period 2 is either $10.50, $3.35, or $0.

At date 1: At date 1, there are two possibilities: Either we have reached

an “up” state, in which case the current stock price is $55 and the option

will pay off $10.50 or $3.35 in the next period:

10.5000

????

3.3500

We use the state prices of q

= 0.6531, q

= 0.2903 to price the option at

this state:

Option price at up state, date“ ” 1 0 6531 10 50 0 2903 3 35 7 83=∗+∗=.....002

The alternative possibility is that we’re in the “down” state of period 1:

3.3500

????

0.0000

Using the same state prices (which, after all, depend only on the “up”

and “down” movements of the stock price and the interest rate), we

get

Option price at down state, date“ ” 1 0 6531 3 35 0 2903 0 2 1880=∗+∗=... .

At date 0: Going backward in this way, we’ve now ﬁ lled in the following

picture:

10.5000

7.8302

????

3.3500

2.1880

0.0000

451 The Binomial Option-Pricing Model

17.4.1 Extending the Binomial Pricing Model to Many Periods

It is clear that the logic of the example can be extended to many periods.

Here’s another Excel graphic showing a ﬁ ve-date model using the same

“up” and “down” parameters as before:

ABCDEFGHIJ

Up, U 1.10

Down, D 0.97 State prices

Interest rate, R 1.06

0.6531 <-- =(B4-B3)/(B4*(B2-B3))

Initial stock price, S 50.00

0.2903 <-- =(B2-B4)/(B4*(B2-B3))

Option exercise price, X 50.00

Stock price Bond price

60.5000 1.1236

55.0000 1.0600

50.0000 53.3500 1.00 1.1236

48.5000 1.0600

47.0450 1.1236

Call option price

*E18+q

*E20

10.5000 <-- =MAX(E9-$B$5,0)

7.8302

5.7492 3.3500 <-- =MAX(E11-$B$5,0)

2.1880

*C19+q

*C21

0.0000 <-- =MAX(E13-$B$5,0)

*E20+q

*E22

BINOMIAL OPTION PRICING WITH STATE PRICES IN

A TWO-PERIOD (THREE-DATE) MODEL

Thus at period 0 the buyer of an option owns a security that will be worth

$7.83 if the underlying stock has an “up” movement in its return and

$2.19 if the stock has a “down” movement in its return. We can again use

the state prices to value this option:

Option price at date 0 0 6531 7 830 0 2903 2 188 5 749=∗+∗=.....

452 Chapter 17

73.2050

Stock price

66.5500

60.5000

64.5535

55.0000

58.6850

50.0000

53.3500 56.9245

48.5000

51.7495

47.0450

50.1970

45.6337

44.2646

1.2625

Bond price

1.1910

1.1236

1.2625

1.0600 1.1910

1.0000

1.1236

1.2625

1.0600

1.1910

1.1236

1.2625

1.1910

1.2625

453 The Binomial Option-Pricing Model

17.4.2 Do You Really Have to Price Everything Backward?

The answer is no. There’s no necessity to price the call price payoffs

“backward” at each node back from the terminal date, as long as the call

is European.

It is enough to price each of the terminal payoffs by the

state prices, providing you count properly the number of paths to each

terminal node. Here’s an illustration, using the same example:

2. When we discuss American options in section 17.5, we will see that backward pricing

is critical.

23.2050

Call price

19.3802

16.0002

14.5535

13.0190

11.5152

10.4360

8.8502

6.9245

6.6593 4.5797

3.0284

0.1970

0.1287

0.0000

Date 0 Date 1 Date 2 Date 3 Date 4

454 Chapter 17

An explanation for the preceding spreadsheet follows. For each termi-

nal option payoff, we consider these questions:

How was this terminal

payoff reached? How many

“up” steps did the stock

make, and how many

“down” steps did it make?

Example: The terminal payoff of 14.5535

arises when the stock price is 64.5535.

This result occurs when the stock price

goes up three times and down once.

What is the price per dollar

of the payoff in the

particular state?

State price =

#up

steps

#down steps

Example: The value at time 0 of the

terminal payoff considered in the same

example is 0.6531

0.2903

= 0.0809

How many paths are there

with the same terminal

payoff?

The answer is given by the

binomial coefﬁ cient

Number of periods

Number of up steps“”

⎛

⎝

⎜

⎞

⎠

⎟

Example: There are

⎛

⎝

⎜

⎞

⎠

⎟

paths which

give the terminal stock price of 64.5535.

The Excel function Combin(4,3) gives

this binomial coefﬁ cient.

What is the value at time 0

of a particular terminal

payoff?

The answer is the product

of the payoff times the

price times the number of

paths.

Example: 14.5535

0.0809

4 = 4.7078

What is the value at time 0

of the option?

The sum of the values of

each payoff.

Total value: 10.4360. This is the

multiperiod call option value in the ﬁ ve-

date (four-period) binomial model.

European puts can be priced either by using the preceding logic or—as

in cell G16—by using put-call parity.

ABCDEFGH

Up, U 1.10

Down, D 0.97

State prices

Interest rate, R 1.06

0.6531 <-- =(B4-B3)/(B4*(B2-B3))

Initial stock price, S 50.00

0.2903 <-- =(B2-B4)/(B4*(B2-B3))

Option exercise price, X 50.00

Number of "up" steps

at terminal date

Number of

"down" steps

at terminal date

Terminal stock

price

= S*U^(# up)

*D^(# down)

Option payoff

at terminal

state

State price for

terminal date

= q

^(# up)

^(# down)

Number of

paths to

terminal state

Value

=payoff*state

price*#paths

4 0 73.2050 23.2050 0.1820 1 4.2224

3 1 64.5535 14.5535 0.0809 4 4.7078

2 2 56.9245 6.9245 0.0359 6 1.4933

1 3 50.1970 0.1970 0.0160 4 0.0126

0 4 44.2646 0.0000 0.0071 1 0.0000

Call price 10.4360 <-- =SUM(G10:G14)

Put price 0.0407 <-- =G15+B6/B4^4-B5

Notes

There are 5 dates in this model (0, 1, ... , 5) but only 4 periods and thus only 4 possible "up" or "down" steps.

The put price in cell G16 is computed using put-call parity: put = call + PV(X) - stock

BINOMIAL OPTION PRICING WITH STATE PRICES

IN A FOUR-PERIOD (FIVE-DATE) MODEL

455 The Binomial Option-Pricing Model

To recapitulate: The price of a European call option in a binomial

model with n periods is given by

Call price max ,

Put price

⎛

⎝

⎜

⎞

⎠

⎟

∗−

−−

∑

ni i ni

qq SUD X

0()

−−

∑

⎛

⎝

⎜

⎞

⎠

⎟

−∗

ni i ni

qq X SUDmax , Direct pricing

Call pri

()

cce Using put-call parity+−

⎧

⎨

⎪

⎩

⎪

In section 17.6 of this chapter we implement these formulas in

VBA.

17.5 Pricing American Options Using the Binomial Pricing Model

We can use the binomial pricing model to calculate the prices of Ameri-

can options as well as European options.

We reconsider the same basic

model, in which Up = 1.10, Down = 0.97, R = 1.06, S = 50, X = 50. We

examine the three-date version of the model. The payoff patterns for the

stock and the bond have been given previously, and it remains only to

consider the payoff patterns for a put option with X = 50. We reference

the states of the world by using the following labels:

State labels

UD or D

Put payoffs at date 3

Here are the values of the stock and the date 3 put payoffs:

3. Recall from Chapter 16 that an American call option on a non-dividend-paying stock

has the same value as a European call option. We return to calls at the end of this

section.

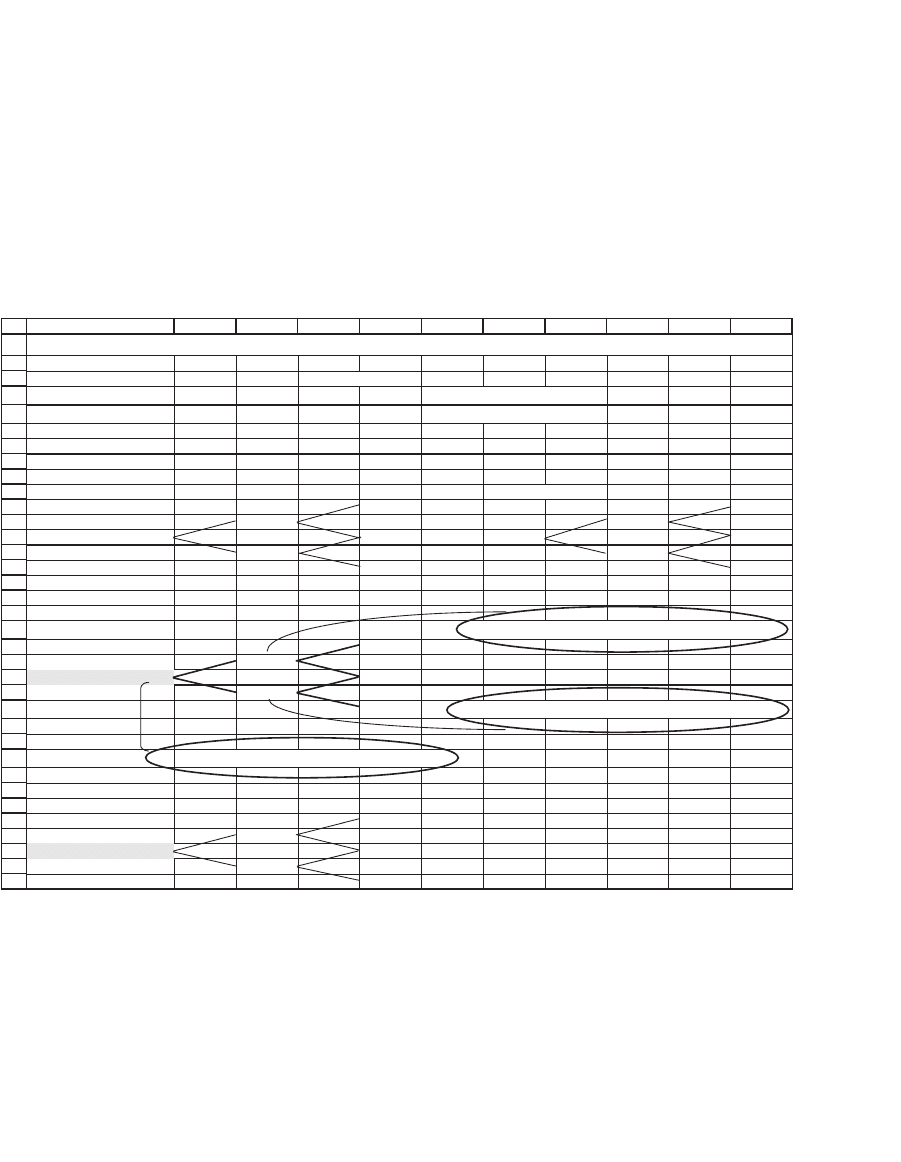
456 Chapter 17

Stock price American put payoffs

60.5000

0.0000

55.0000

????

50.0000

53.3500

???? 0.0000

48.5000

????

47.0450

2.9550

At date 2, the holder of an American put can choose whether to hold

the put or to exercise it. We now have the following value function:

Put value

at date 2

state U

max

Put value if exercised max ,

=−

()

UUD

UU q∗+∗

⎧

⎨

⎩

Put payoff in state Put payoff in state UD

A similar function holds for the put value in state D at date 2. The result-

ing tree now looks like this:

American put payoffs

0.0000

????

0.0000

1.5000

2.9550

Here’s the explanation:

•

In state U, the put is valueless. When the stock price is $55, it is not

worthwhile to early-exercise the put, since max(X − S

, 0) = max(50 − 55,

0) = 0. However, since the future put payoffs from state U are zero, the

state-dependent present value of these future payoffs (the second line

in the previous formula) is also zero.

•

In state D, however, the holder of the put gets max(50 − 48.5, 0) = 1.5

if he exercises the put; however, if he holds the put without exercise, its

market value is the state-dependent value of the future payoffs:

∗+ ∗ = ∗+ ∗ =0 2 96 0 6531 0 0 2903 2 95 0 8578.. . ..

It is clearly preferable to exercise the put in this state rather than hold

onto it.

457 The Binomial Option-Pricing Model

We can use the same logic to price an American call option, though—

following Proposition 2 of Chapter 16—we know that the value of an

American and a European call should coincide. And so they do:

ABCDEFGHIJ

Up, U 1.10

Down, D 0.97

State prices

Interest rate, R 1.06

0.6531 <-- =(B4-B3)/(B4*(B2-B3))

Initial stock price, S 50.00

0.2903 <-- =(B2-B4)/(B4*(B2-B3))

Option exercise price, X 50.00

Stock price Bond price

60.5000 1.1236

55.0000 1.0600

50.0000 53.3500 1.0000 1.1236

48.5000 1.0600

47.0450 1.1236

American put option

=MAX(MAX(X-S*U,0),q

*put_payoff

)

0.0000

0.4354 0.0000

1.5

2.9550

=MAX(MAX(X-S*D,0),q

*put_payoff

)

=MAX(MAX(X-S,0),q

*put_value

)

European put option

0.0000

0.2490 0.0000

0.8578

2.9550

AMERICAN PUT PRICING IN A TWO-PERIOD MODEL

At date 0, a similar value function recurs:

Put value

at date 0

max

Put value if exercised max , 0)

Put pa

=−

∗

(XS

yyoff in state Put payoff in state DUq

+∗

⎧

⎨

⎩

Here is the spreadsheet: