Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

428 Chapter 16

16.4.2.2 Payoff Pattern from a Written Call

In options markets the purchaser of a call buys the call from a counter-

party who issues the call. In the jargon of options, the issuer of the call

is called the call writer. It is worthwhile to spend a few minutes consider-

ing the difference between the security bought by the call purchaser and

the call writer:

•

The call purchaser buys a security that gives the right to buy a share

of stock on or before date T for price X. The cost of this privilege is

the call price C

, which is paid at the time of the call purchase. Thus

the call purchaser has an initial negative cash ﬂ ow (the purchase

price C

); however, his cash ﬂ ow at date T is always nonnegative:

max (S

− X, 0).

•

The call writer gets C

at the date of the call purchase. In return

for this price, the writer of the call agrees to sell a share of the stock

for price X on or before date T. Notice that whereas the call pur-

chser has an option, the call writer has undertaken an obligation.

Furthermore, note that the cash ﬂ ow pattern of the call writer is

opposite to that of the call purchaser: The writer’s initial cash ﬂ ow

is positive (+C

), and her cash ﬂ ow at date T is always nonpositive:

−max (S

− X, 0).

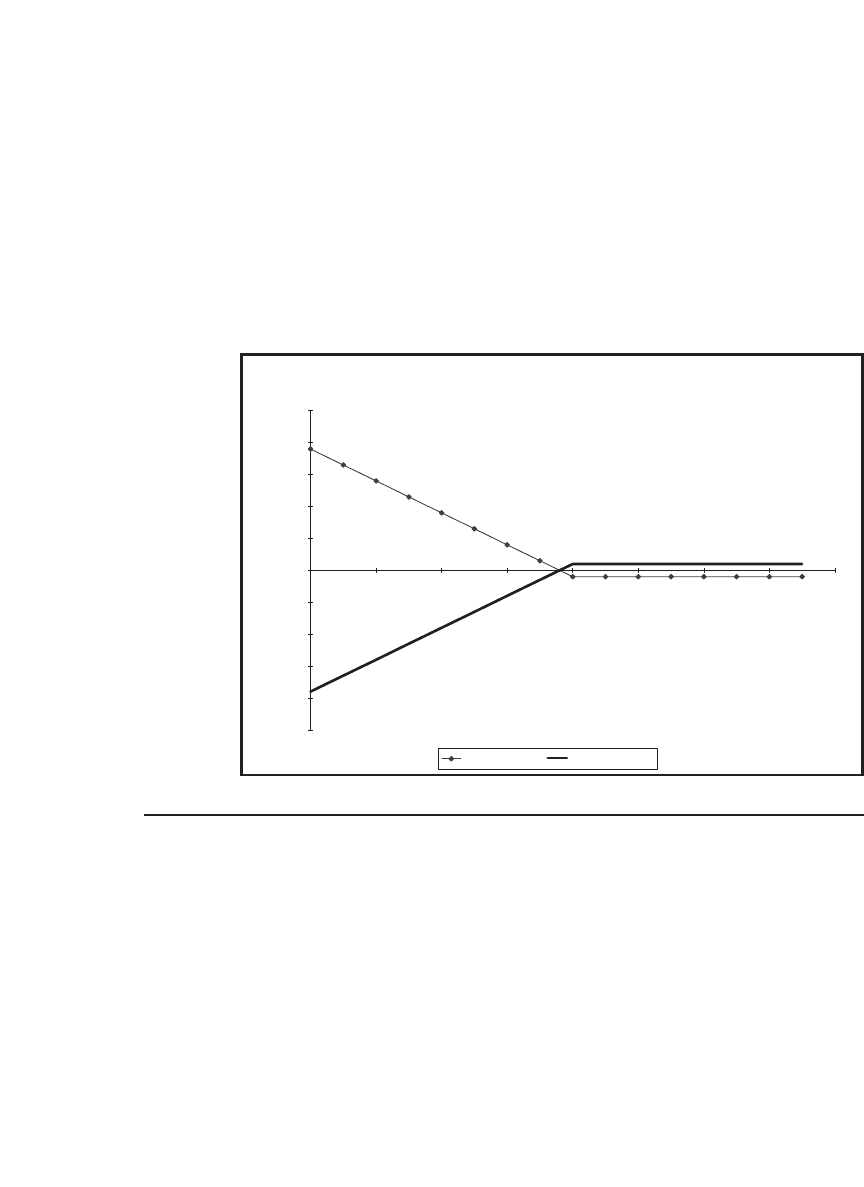
The proﬁ t of a call writer is the opposite of that of the call purchaser.

For the case of the GP options,

Call writer’s proﬁ t in September

=− −

+≤

−>

⎧

⎨

⎩

CSX

4040

440

44 40

max ( )

Graphing the proﬁ t patterns of the bought and the written call gives:

429 An Introduction to Options

16.4.3 Put Option Proﬁ t Patterns

16.4.3.1 Payoff Pattern from a Purchased Put

If in July you bought one GP September 40 put for $2, then in September

you will exercise the put only if the market price of GP is lower than

$40. If we write the initial (July) put price as P

, we can write the proﬁ t

function from the put in September as follows:

Put proﬁ t in September =−−

=−−

−≤

−>

⎧

⎨

⎩

max ( )

040 2

38 40

240

XS P

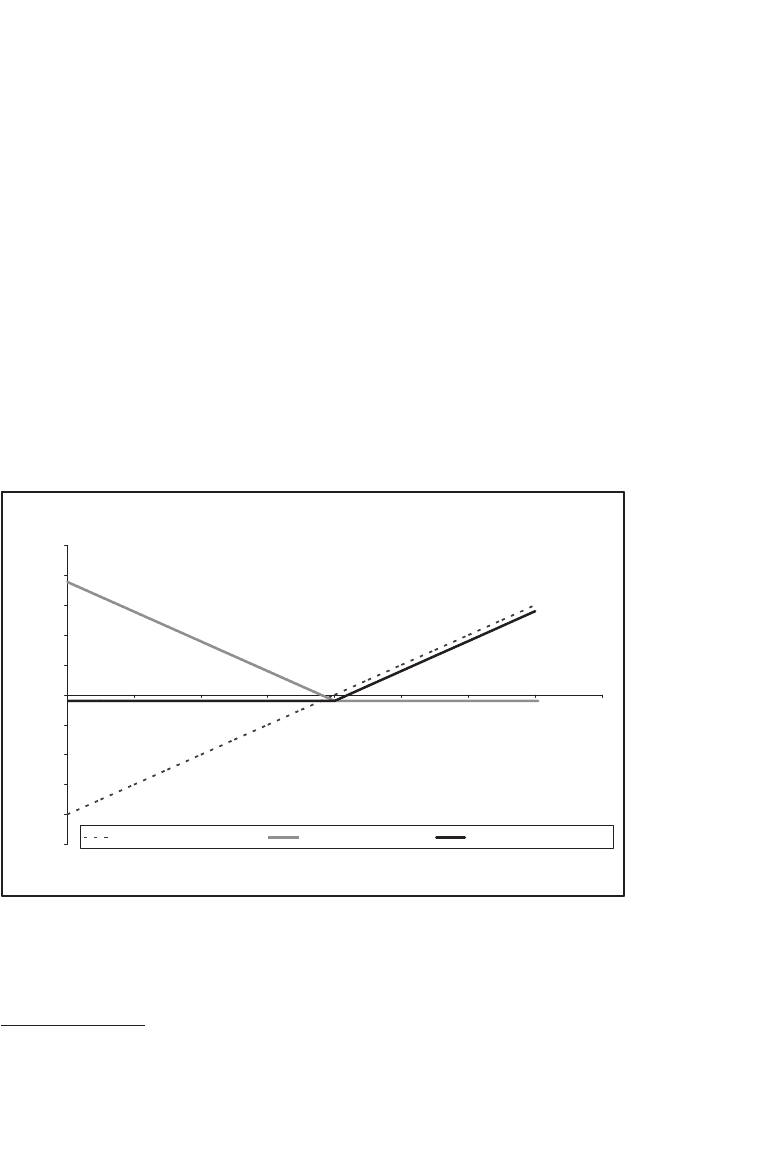
16.4.3.2 Payoff Pattern from a Written Put

The put writer obligates herself to purchase one share of GP stock on or

before date T for the put exercise price of X. For putting herself in this

invidious position, the writer of the put receives, at the time the put

is written, the put price P

. The payoff pattern from writing the GP

September 40 put is therefore

Call Option Profit Patterns

–40

–30

–20

–10

0 1020304050607080

Terminal stock price, S

($)

Profit ($)

Bought call Written call

430 Chapter 16

Put writer’s profit in September ,

=− −

PXS

2040

max ( )

−+ ≤

⎧

⎨

⎩

38 40

240

Graphing the proﬁ t patterns of the bought and the written put gives the

following:

Put Option Profit Patterns

–50

–40

–30

–20

–10

0 1020304050607080

Terminal stock price, S

($)

Profit ($)

Bought put Written put

16.5 Option Strategies: Payoffs from Portfolios of Options and Stocks

There is some interest in graphing the combined proﬁ t pattern from a

portfolio of options and stocks. These patterns give an indication of how

options can be used to change the payoff patterns of “standard” securities

such as stocks and bonds. Here are a few examples.

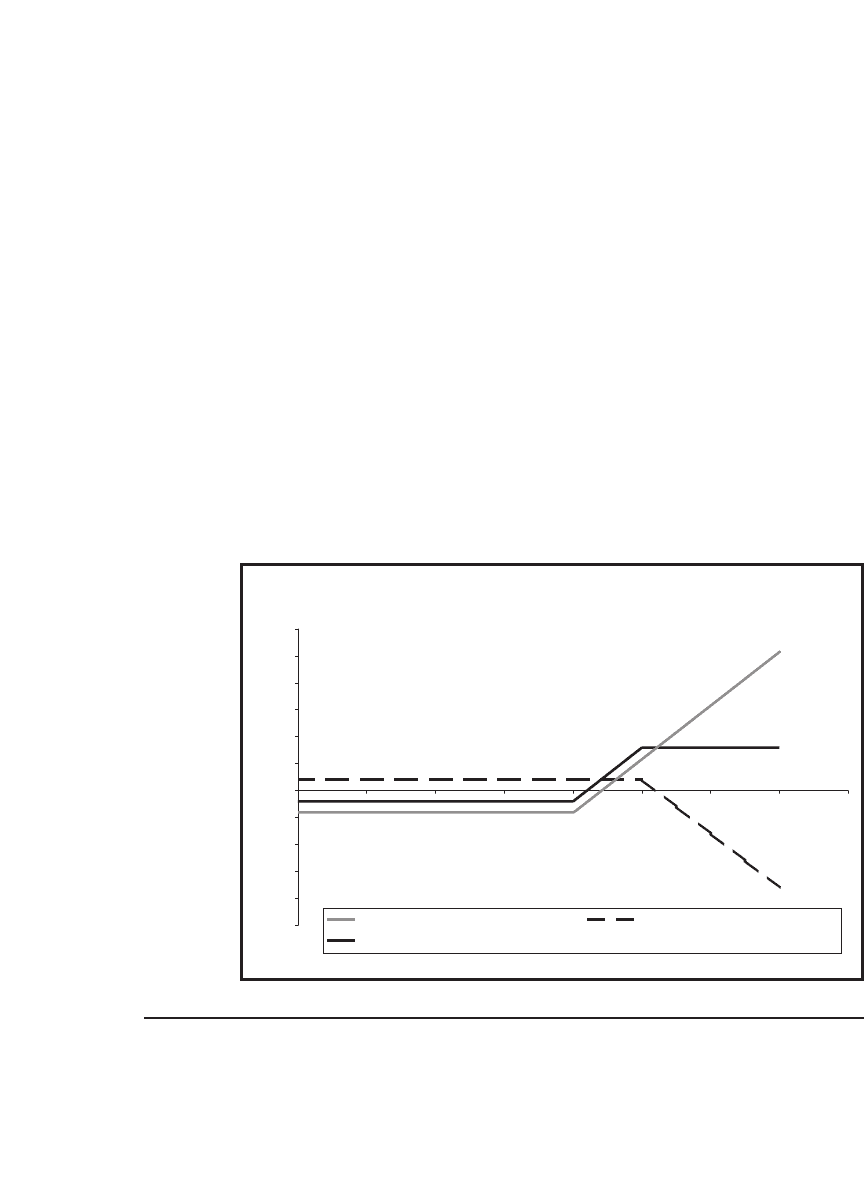
16.5.1 The Protective Put

Consider the following combination:

•

One share of stock, purchased for S

•

One put, purchased for P with exercise price X.

431 An Introduction to Options

This option strategy is often called a “protective put” strategy or “port-

folio insurance”; in Chapter 21 we return to this topic, exploring it

in much further detail. The payoff pattern of the protective put is

given by

Stock proﬁ t + Put proﬁ t

=−+ − −

−+−−

−−

⎧

⎨

⎩

−−

−

SS XS P

SSXSP

SSP

XS P

0max ( ),

000

−

⎧

⎨

⎩

≤

When applied to the GP example (that is, buying a share at $40 and a

put with X = $40 for $2) this strategy gives the following graph:

Protective Put Profit

–50

–40

–30

–20

–10

0 10203040506070

Terminal stock price, S

($)

Profit ($)

Terminal stock profit Terminal put profit Protective put profit

This pattern looks very much like the payoff patterns from a call.

6. In section 16.6 we prove and illustrate the put-call parity theorem. It follows from this

theorem that a call must be priced at a price C such that C = P + S

− Xe

−rT

. Thus, when

calls are correctly priced according to this theorem, the payoff from a put + stock

combination is the same as that from a call + bond combination.

432 Chapter 16

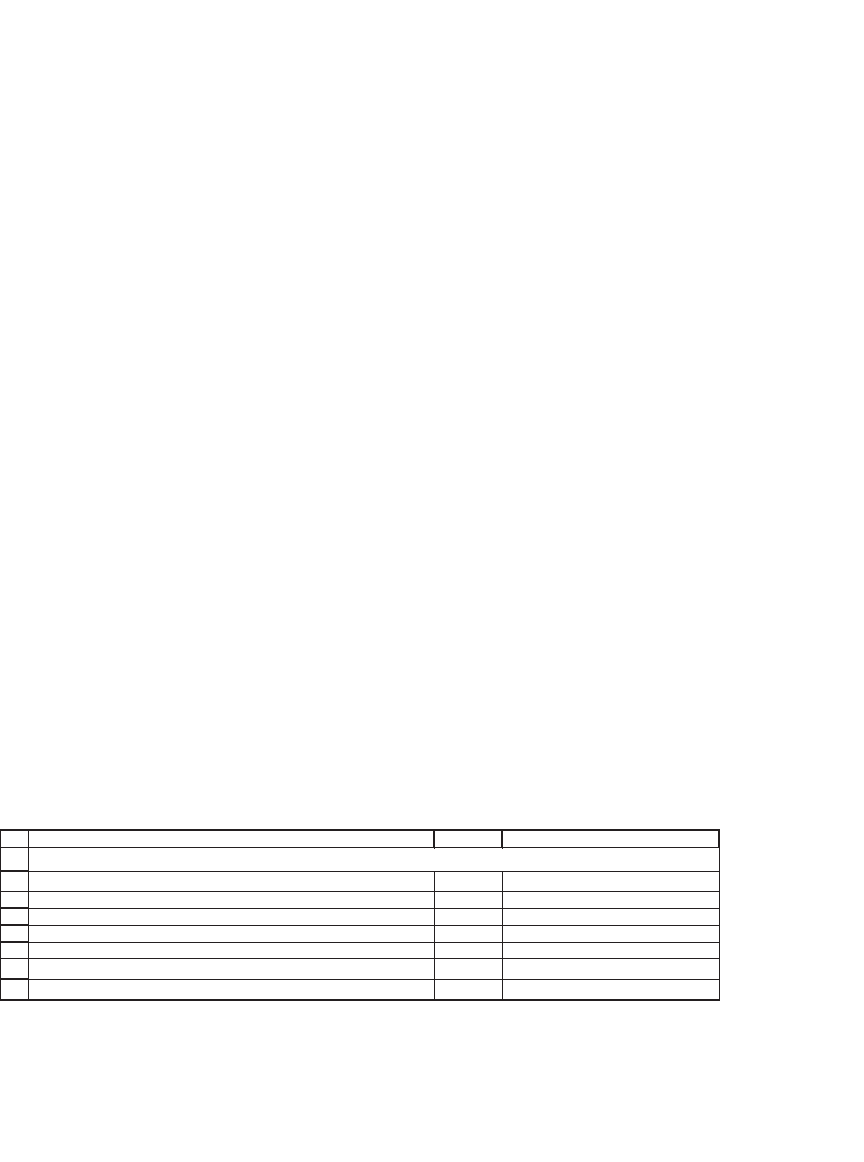
16.5.2 Spreads

Another combination involves buying and writing calls with different

exercise prices. When the bought call has a low exercise price and the

written call has a higher exercise price, the combination is called a bull

spread. As an example, suppose you bought a call (for $4) with an exer-

cise price of $40 and wrote a call (for $2) with an exercise price of $50.

This bull spread gives a proﬁ t of

max ( ) [max ( ) ]SS

−−− −−

−+

−−+=−

−−

40 0 4 50 0 2

40 4 2 42

40 4

−−−−=

⎧

⎨

⎪

⎩

⎪

≤

≤≤

≥()S

50 2 8

40 50

The following Excel graph shows each of the two calls and the resulting

spread proﬁ t:

Bull Spread Profit Chart

–25

–20

–15

–10

–5

0 10203040506070

Terminal stock price, S

($)

Profit ($)

Terminal purchased call, X = 40 Terminal written call, X = 50

Terminal spread profit

16.6 Option Arbitrage Propositions

In succeeding chapters we price options given speciﬁ c assumptions about

the probability distribution of the underlying asset (usually the stock) on

433 An Introduction to Options

which the option is written. However, there is much that can be learned

about the pricing of options without making these speciﬁ c probability

assumptions. In this section we consider a number of these arbitrage

restrictions on option pricing. Our list is by no means exhaustive, and we

have concentrated on those propositions which provide insight into the

pricing of options or that will be used in later sections.

Throughout we assume that there is a single risk-free interest rate that

prices bonds; we also assume that this risk-free rate is continuously com-

pounded, so that the present value of a riskless security that pays off X

at time T is given by e

−rT

proposition 1 Consider a call option written on a stock that pays no

dividends before the option’s expiration date T. Then the lower bound

on a call option price is given by

CSXe

0≥−

−

max ( ),

Comment Before proving this proposition, it will be helpful to consider

its meaning: Suppose that the riskless interest rate is 10 percent, and

suppose we have an American call option with maturity T = 1/2 (i.e., the

expiration date of the option is one-half year from today) with X = 80

written on a stock whose current stock price S

= 83. A naive approach

to determining a lower bound on this option’s price would be to state

that it is worth at least $3, since it could be exercised immediately with

a proﬁ t of $3. Proposition 1 shows that the option’s value is at least 83 −

−0.10

0.5

80 = 6.90. Furthermore, a careful examination of the following

proof will show that this fact does not depend on the option being an

American option—it is also true for a European option.

Current stock price, S

Option time to maturity, T 0.5

Option exercise price, X 80

Interest rate, r 10%

Naive minimum option price, Max(S

-X,0)

=MAX(B2-B4,0)

Proposition 1 lower bound on option price, Max(S

- Exp(-rT)X,0)

6.902 <

=MAX(B2-EXP(-B5*B3)*B4,0)

Proposition 1--Higher Lower Bounds for Call Prices

Proof Standard arbitrage proofs are built on the consideration of the

cash ﬂ ows from a particular strategy. In this case the strategy is the

following:

434 Chapter 16

At time 0 (today):

•

Buy one share of the stock.

•

Borrow the present value (PV) of the option exercise price X.

•

Write a call on the option.

At time T:

•

Exercise the option if it is proﬁ table to do so.

•

Repay the borrowed funds.

This strategy produces the following cash ﬂ ow table:

Today

At Time T

Action Cash Flow

< XS

≥ X

Buy stock

−S

Borrow PV of X +Xe

−rT

−X −X

Write call

−(S

− X)

Total

−S

+ Xe

−rT

+ C

− X ≤ 0

Note that at time T, the cash ﬂ ow resulting from this option is either

negative (if the call is not exercised) or zero (when S

≥ X). Now a ﬁ nan-

cial asset (in this case, the combination of purchasing a stock, borrowing

X, and writing a call) that has only nonpositive payoffs in the future must

have a positive initial cash ﬂ ow; therefore,

CSXe CSXe

rT rT

00 00

0−+ > >−

−−

To ﬁ nish the proof, we note that in no case can the value of a call be less

than zero. Thus we have that C

≥ max (S

− Xe

−rT

, 0), which proves the

proposition.

Proposition 1 has an immediate and very interesting consequence: In

many cases the early-exercise feature of an American call option is

worthless; therefore, an American call option can be valued as if it were

a European call. The precise conditions are the following:

435 An Introduction to Options

proposition 2 Consider an American call option written on a stock that

will not pay any dividends before the option’s expiration date T. Then it

is never optimal to exercise the option before its maturity.

Proof Suppose the holder of the option is considering exercising it

early, at some date t < T. The only reason to consider such early exercise

is that S

− X > 0, where S

is the price of the underlying stock at time t.

However, by Proposition 1 the market value of the option at time t

is at least S

− Xe

−r(T−t)

, where r is the risk-free rate of interest. Since

− Xe

−r(T−t)

> S

− X, it follows that the option’s holder is better off

selling the option in the market than exercising it.

Proposition 2 means that many American call options can be priced

as if they were European calls. Note that this statement is not true for

American puts, even if the underlying stock pays no dividends (we give

an example in Chapter 19).

proposition 3 (put bounds) The lower bound on the value of a put

option is

PXeS

0≥−

−

max ( ),

Proof The proof of this proposition has the same form as the proof of

the previous theorem. We set up a table of strategies:

Today

At Time T

Action Cash Flow

< XS

≥ X

Short stock

−S

Lend PV of X −Xe

−rT

+X +X

Write put

−(X − S

)

Total

+ S

− Xe

X − S

≤ 0

Since the strategy has only negative or zero payoffs in the future, it must

have a positive cash ﬂ ow today, so that we can conclude that

PXe S

0−+≥

−

Combined with the fact that in no case can a put value be negative, this

proves the proposition.

436 Chapter 16

proposition 4 (put-call parity) Let C

be the price of a European call

with exercise price X written on a stock whose current price is S

. Let P

be the price of a European put on the same stock with the same exercise

price X. Suppose both put and call have exercise date T, and suppose

that the continuously compounded interest rate is r. Then,

CXe PS

000

+=+

−

Proof The proof is similar in style to that of the two previous proposi-

tions. We consider a combination of the four assets (the put, the call, the

stock, and a bond), and show that the pricing relation must hold.

Today

At Time T

Action Cash Flow

< XS

≥ X

Buy call

−C

− X

Buy a bond with payoff X

at time T

−Xe

−rT

Write a put

−(X − S

)

Short one share of the stock

−S

Total

−C

− Xe

−rT

+ P

+ S

Since the strategy has future payoffs that are zero no matter what

happens to the price of the stock, it follows that the initial cash ﬂ ow of

the strategy must also be zero.

Therefore,

CXe PS

000

0+−−=

−

which proves the proposition.

Put-call parity states that the stock price S

, the price of a call C

with

exercise price X and the price of a put P

with exercise price X, are

simultaneously determined with the interest rate r. Following is an illus-

tration which uses the call price C

, the option exercise price X, the

current stock price S

, and the interest rate r to compute the price of a

put with exercise price X and time to maturity T:

7. This is a fundamental fact of ﬁ nance: If a ﬁ nancial strategy has future payoffs that are

identically zero, then its current cost must also be zero. Likewise, if a ﬁ nancial strategy

has future payoffs that are nonnegative, then its time-zero payoff must be negative

(that is, it must cost something).

437 An Introduction to Options

proposition 5 (call option price convexity) Consider three European

calls, all written on the same non-dividend-paying stock and with the

same expiration date T. We suppose that the exercise prices on the calls

are X

, X

, and X

, and denote the associated call prices by C

, C

, and

. We further assume that

. Then,

It follows that the call option price is a convex function of the exercise

price.

Proof To prove the proposition, we consider the following strategy:

At Time 0

At Time T

Action Cash Flow

< X

≤ S

< X

≤ S

< X

≤ S

Buy call with

exercise price

−C

− X

Buy call with

exercise price

−C

00 0

− X

Write two calls

with exercise

price X

+2C

−2(S

− X

) −2(S

− X

)

Total

− C

− X

≥ 02X

− X

− S

= X

− S

> 0

Option exercise price, X 60

Interest rate, r 10%

CBA

Current stock price, S

Option time to maturity, T 0.5

Call price, C

Put price, P

5.0738 <

=B6+B4*EXP(-B5*B3)-B2

Put-Call Parity

from the call price

terest rate r, the time to maturityT, and the ex e X.

This spreadsheet uses put-call parity to derive the put price P

, the in ercise pric