Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

458 Chapter 17

17.6 Programming the Binomial Option-Pricing Model in VBA

The pricing procedure used in the preceding examples can easily be

programmed using Excel’s VBA programming language. In the binomial

model the price can move up or down in any time period. If q

is the

state price associated with an up move and if q

is the state price associ-

ated with a down move, then the binomial European option prices are

given by

Binomial European call max ,=

⎛

⎝

⎜

⎞

⎠

⎟

∗−

−−

∑

ni i ni

qq SUD X

0())

Binomial European put

max ,

⎛

⎝

⎜

⎞

⎠

⎟

−∗

−−

∑

ni i ni

qq X SUD

(()

⎧

⎨

⎪

⎩

⎪

or by put-call parity

ABCDEFGHIJ

Up, U 1.10

Down, D 0.97

State prices

Interest rate, R 1.06

0.6531 <-- =(B4-B3)/(B4*(B2-B3))

Initial stock price, S 50.00

0.2903 <-- =(B2-B4)/(B4*(B2-B3))

Option exercise price, X 50.00

Stock price Bond price

60.5000 1.1236

55.0000 1.0600

50.0000 53.3500 1.0000 1.1236

48.5000 1.0600

47.0450 1.1236

American call option

=MAX(MAX(S*U-X,0),q

*call_payoff

)

10.5000

7.8302

5.7492 3.3500

2.1880

0.0000

=MAX(MAX(S*D-X,0),q

*call_payoff

)

=MAX(MAX(S-X,0),q

*call_value

)

European call option

10.5000

7.8302

5.7492 3.3500

2.1880

0.0000

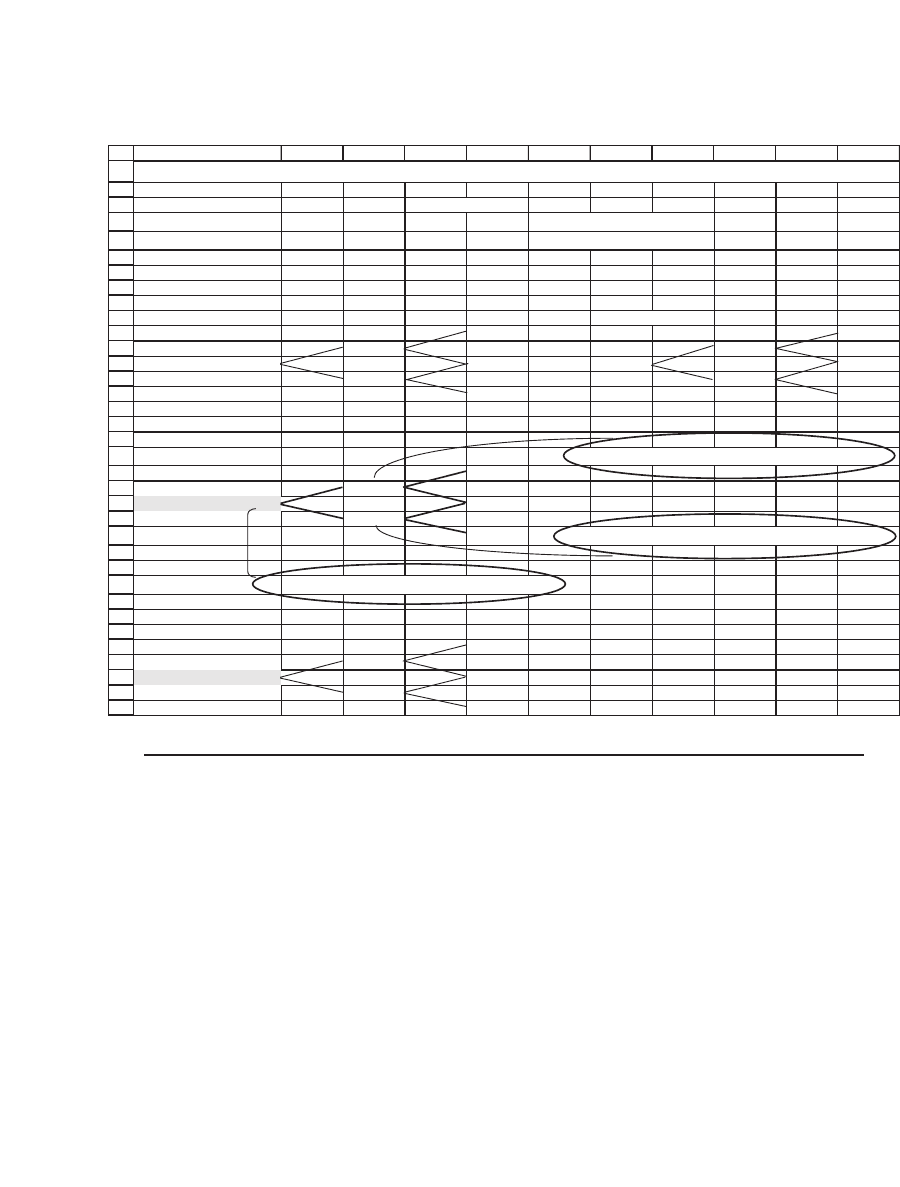
AMERICAN CALL PRICING IN A TWO-PERIOD MODEL

459 The Binomial Option-Pricing Model

where U is an up move, R is a down move in the stock price, and

⎛

⎝

⎜

⎞

⎠

⎟

the binomial coefﬁ cient (the number of up moves in n total moves):

ini

⎛

⎝

⎜

⎞

⎠

⎟

−

!( )!

We use Excel’s Combin(n,i) to give values for the binomial

coefﬁ cients.

Following are two VBA functions that compute the value of binomial

European calls and puts. The function Binomial_eur_put uses put-call

parity to price the put.

Function Binomial_eur_call(Up, Down, Interest, Stock, _

Exercise, Periods)

q_up = (Interest - Down) / (Interest * (Up - Down))

q_down = 1 / Interest - q_up

Binomial_eur_call = 0

For Index = 0 To Periods

Binomial_eur_call = Binomial_eur_call _

+ Application.Combin(Periods, Index) * _

q_up ^ Index * _

q_down ^ (Periods - Index) * _

Application.Max(Stock * Up ^ Index * Down ^ _

(Periods - Index) - Exercise, 0)

Next Index

End Function

Function Binomial_eur_put(Up, Down, Interest, Stock, _

Exercise, Periods)

Binomial_eur_put = Binomial_eur_call(Up, Down, _

Interest, _ Stock, Exercise, Periods) _

+ Exercise / Interest ^ Periods - Stock

End Function

Implementing this procedure in a spreadsheet, we get for the four-

period example of section 17.4:

460 Chapter 17

17.6.1 American Put Pricing

As discussed in Chapter 16, a well-known theorem states that the price

of an American call on a non-dividend-paying stock is the same as that

of a European option. The pricing of American put, however, can be

different. The following VBA function uses a binomial option-pricing

model like the one from section 17.5 to price American puts:

CBA

Up, U 1.10

Down, D 0.97

Interest rate, R 1.06

Initial stock price, S 50.00

Option exercise price, X 50.00

Number of periods, n 4

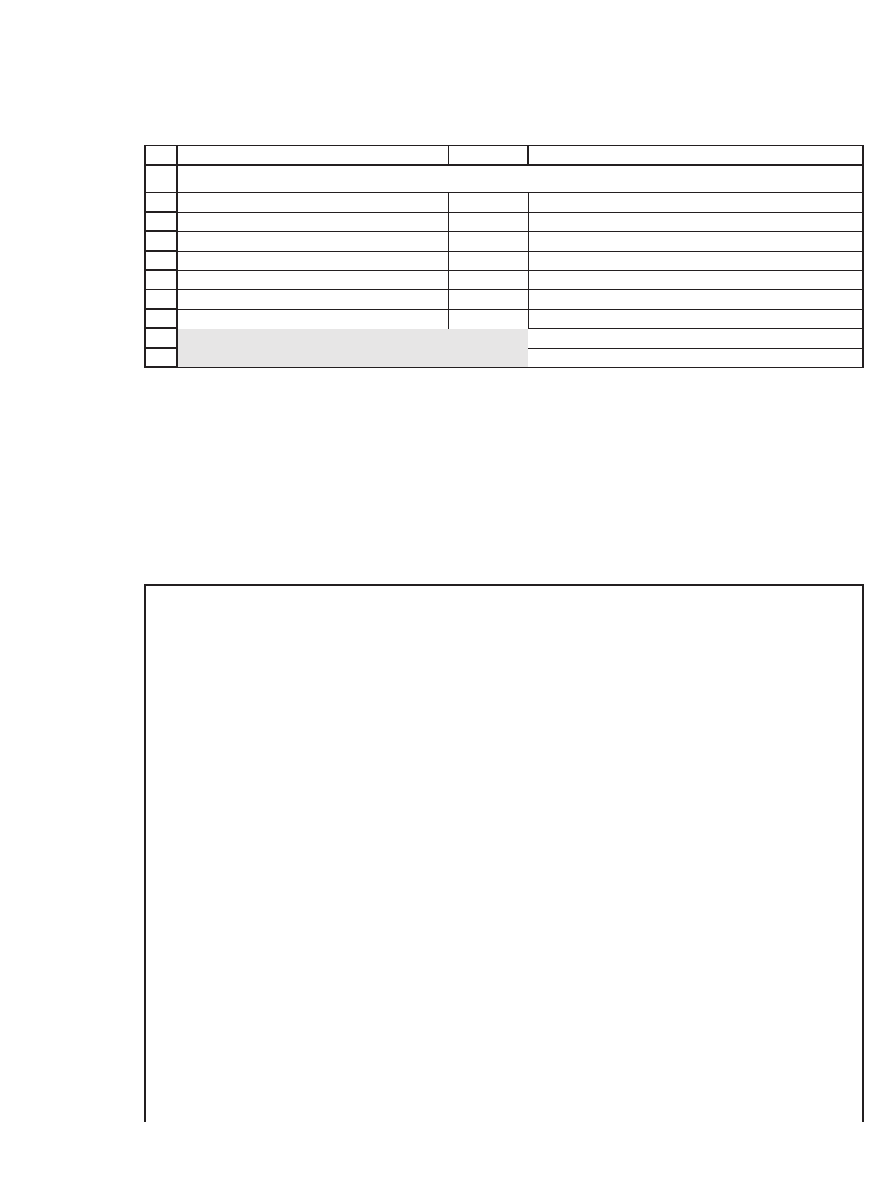
European call 10.4360 <-- =binomial_eur_call(B2,B3,B4,B5,B6,B7)

European put 0.0407 <-- =binomial_eur_put(B2,B3,B4,B5,B6,B7)

VBA FUNCTIONS FOR CALLS AND PUTS

Function Binomial_amer_put(Up, Down, Interest, Stock, _

Exercise, Periods)

q_up = (Interest - Down) / (Interest *

(Up - Down))

q_down = 1 / Interest - q_up

Dim OptionReturnEnd() As Double

Dim OptionReturnMiddle() As Double

ReDim OptionReturnEnd(Periods + 1)

For State = 0 To Periods

OptionReturnEnd(State) = _

Application.Max(Exercise - Stock * Up ^ _

State * Down ^ _

(Periods - State), 0)

Next State

For Index = Periods - 1 To 0 Step -1

ReDim OptionReturnMiddle(Index)

For State = 0 To Index

OptionReturnMiddle(State) = _

Application.Max(Exercise - Stock * Up ^ _

State * Down ^ _

461 The Binomial Option-Pricing Model

In this function we use two arrays, called OptionReturnEnd and

OptionReturnMiddle. At each date t, these arrays store the option values

for the date itself and the next date—t + 1.

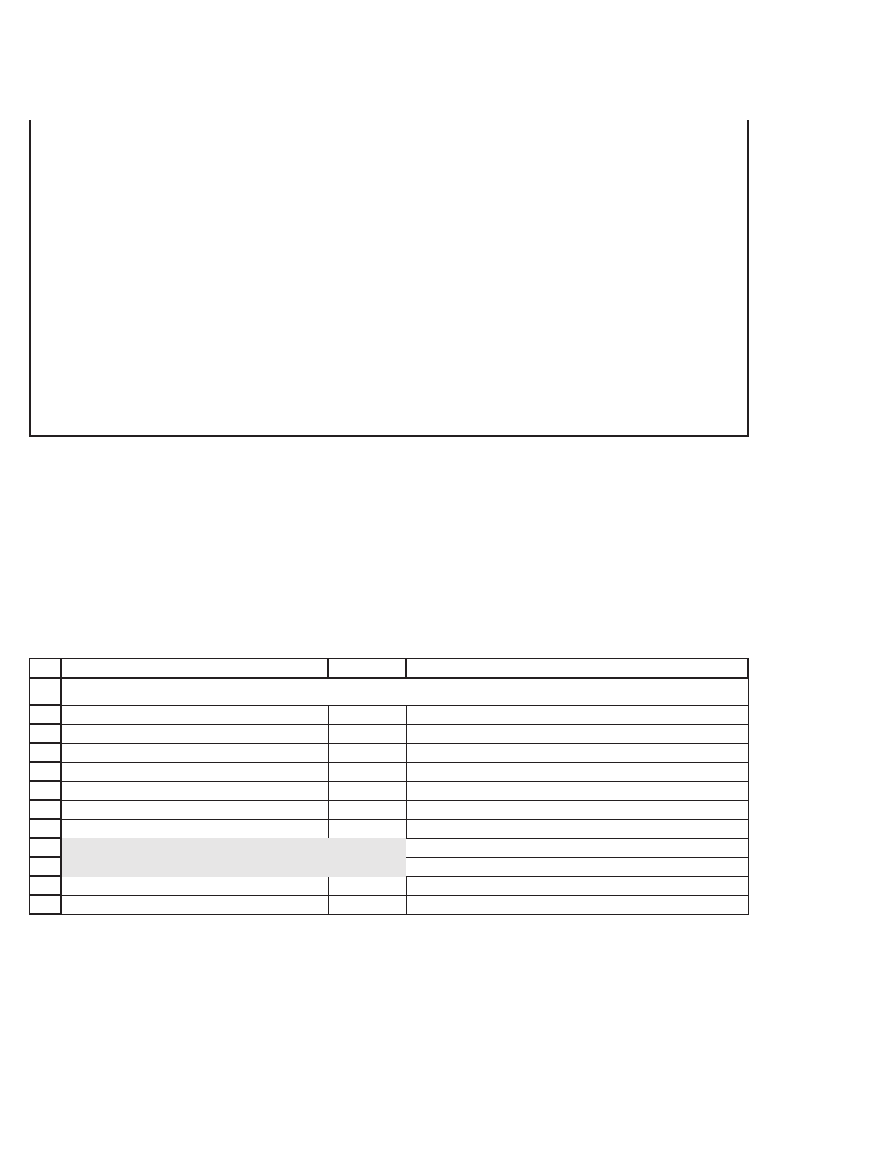
Here’s an implementation in a spreadsheet, using the two-period,

three-date example from section 17.5:

(Index - State), q_down * _

OptionReturnEnd(State) + q_up * _

OptionReturnEnd(State + 1))

Next State

ReDim OptionReturnEnd(Index)

For State = 0 To Index

OptionReturnEnd(State) = _

OptionReturnMiddle(State)

Next State

Next Index

Binomial_amer_put = OptionReturnMiddle(0)

End Function

CBA

Up, U 1.10

Down, D 0.97

Interest rate, R 1.06

Initial stock price, S 50.00

Option exercise price, X 50.00

Number of periods, n 2

American put 0.4354 <-- =binomial_amer_put(B2,B3,B4,B5,B6,B7)

European put 0.2490 <-- =binomial_eur_put(B2,B3,B4,B5,B6,B7)

American call 5.7492 <-- =binomial_amer_call(B2,B3,B4,B5,B6,B7)

European call 5.7492 <-- =binomial_eur_call(B2,B3,B4,B5,B6,B7)

VBA FUNCTIONS FOR CALLS AND PUTS

The values in cells B9 and B10 are for an American and a European

put; these values correspond to those given in section 17.5. In cell B11

we use a function similar to the American put function to price American

calls. Unsurprisingly—given Proposition 2 of Chapter 16—this function

gives the same value as the binomial European call-pricing function.

462 Chapter 17

The VBA function works well for many more periods.

In the example

that follows we calculate the value of an American put and call for

options that expire at T = 0.75 of a year. The stochastic process that

deﬁ nes the stock returns has mean m = 15 percent and standard deviation

σ = 35 percent. The annual continuously compounded interest rate r is 6

percent, and each year is divided into 25 subperiods, so that a single

period has length Δt = 1/25 = 0.04. Given these numbers, Up, Down, and

R are deﬁ ned by

Up Down e===

+−

eeR

tt tt rt

μσ μσ

ΔΔ ΔΔ Δ

,,.

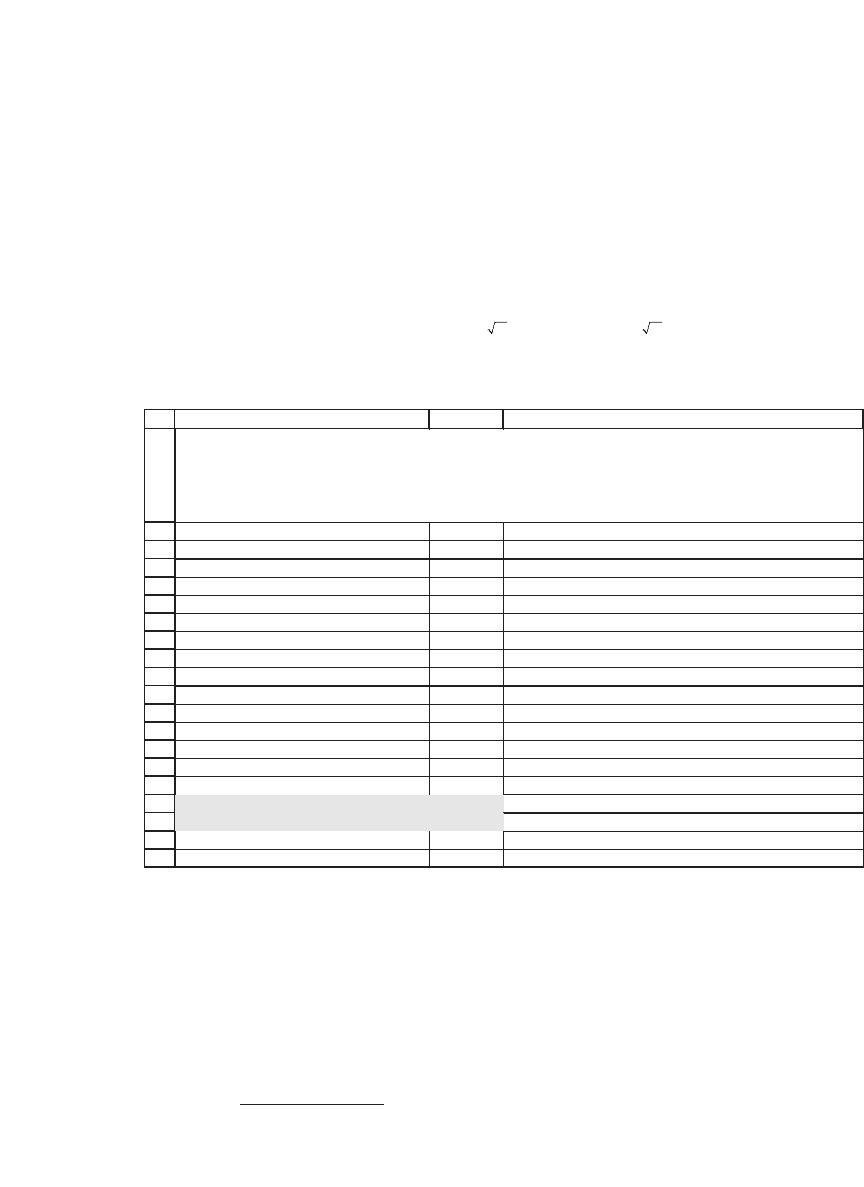
Here is the pricing of an American and European call and put:

4. The discussion that follows is perhaps best read after Chapters 18 and 19.

CBA

Mean return per year,

15%

Standard deviation of annual return,

35%

Annual interest rate, r 6%

Initial stock price, S 50.00

Option exercise price, X 50.00

Option exercise date (years) 0.75

Number of divisions of 1 year 25 <-- each year divided into 25 subperiods

t, the length of one division

0.04 <-- =1/B9

Up move per

1.078963 <-- =EXP(B2*B10+B3*SQRT(B10))

Down move per

0.938005 <-- =EXP(B2*B10-B3*SQRT(B10))

Interest rate per

1.002403 <-- =EXP(B4*B10)

Number of periods until maturity, n 19 <-- =ROUND(B8*B9,0)

American put 5.1311 <-- =binomial_amer_put(B11,B12,B13,B6,B7,B15)

European put 4.9213 <-- =binomial_eur_put(B11,B12,B13,B6,B7,B15)

American call 7.1501 <-- =binomial_amer_call(B11,B12,B13,B6,B7,B15)

European call 7.1501 <-- =binomial_eur_call(B11,B12,B13,B6,B7,B15)

VBA FUNCTIONS FOR CALLS AND PUTS

n divisions per year,

t = 1/n

Up=exp(

t +

*sqrt(

t)), Down = exp(

t -

*sqrt(

t))

Notice that we have compromised on the number of periods, by using

Excel’s Round function—since there are 25 divisions of one year and the

option’s maturity is T = 0.75, the actual number of periods to maturity

is 25

0.75, which is not a round number.

This procedure works well even for a very large number of periods. In

the next example, the option has a maturity T = 0.5, and the basic one-

year period is divided into 400 subperiods. Excel easily computes the

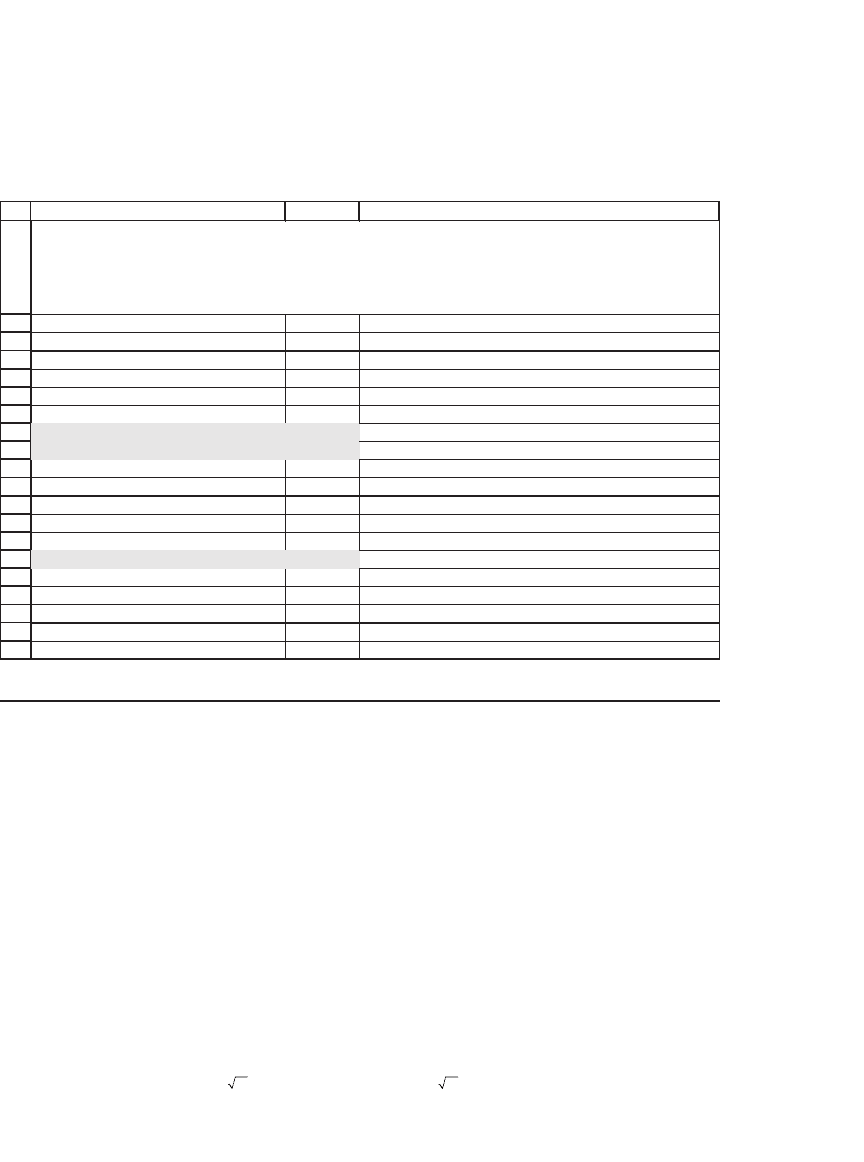
463 The Binomial Option-Pricing Model

value of the American put and call, even though a considerable amount

of computation is involved.

CBA

Mean return per year,

15%

Standard deviation of annual return,

35%

Annual interest rate, r 6%

Initial stock price, S 50.00

Option exercise price, X 50.00

Option exercise date (years) 0.50

Number of divisions of 1 year 400 <-- each year divided into 400 subperiods

t, the length of one division

0.0025 <-- =1/B9

Up move per

1.018036 <-- =EXP(B2*B10+B3*SQRT(B10))

Down move per

0.983021 <-- =EXP(B2*B10-B3*SQRT(B10))

Interest rate per

1.00015 <-- =EXP(B4*B10)

Number of periods until maturity, n 200 <-- =ROUND(B8*B9,0)

American put 4.2882 <-- =binomial_amer_put(B11,B12,B13,B6,B7,B15)

European put 4.1471 <-- =binomial_eur_put(B11,B12,B13,B6,B7,B15)

American call 5.6248 <-- =binomial_amer_call(B11,B12,B13,B6,B7,B15)

European call 5.6248 <-- =binomial_eur_call(B11,B12,B13,B6,B7,B15)

VBA FUNCTIONS FOR CALLS AND PUTS

n divisions per year,

t = 1/n

Up=exp(

t +

*sqrt(

t)), Down = exp(

t -

*sqrt(

t))

17.7 Convergence of Binomial Pricing to the Black-Scholes Price

In this section we discuss the convergence of the binomial model to the

Black-Scholes pricing formula. The discussion assumes some understand-

ing of lognormality (discussed in Chapter 18) and the Black-Scholes

option-pricing formula (discussed in Chapter 19). So you may want to

skip this section and come back to it later.

Whenever we consider a ﬁ nite approximation to the option-pricing

formulas, we have to use an approximation to the up and the down move-

ments. One widespread translation of the interest rate r and the stock’s

volatility σ to an “up” or “down” move necessary for the binomial model

ΔΔ

tTn Re

UeD e

=+ = =+ =

−

Up Down11

σσ

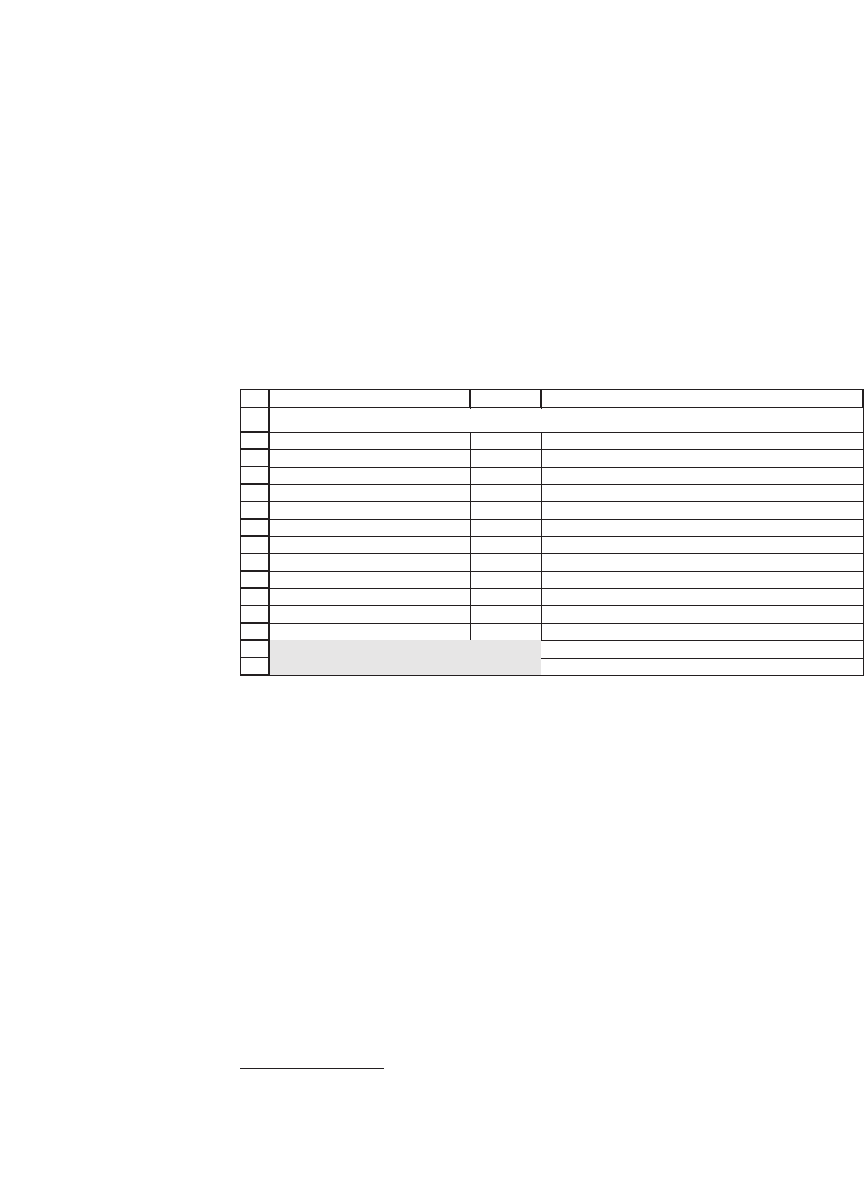
464 Chapter 17

This approximation guarantees that as Δt → 0 (i.e., as n → ∞), the result-

ing distribution of the stock returns approaches the lognormal

distribution.

An implementation of this methodology in a spreadsheet follows. The

function Binomial_Eur_call is the same as that deﬁ ned previously; the

function BSCall is the Black-Scholes formula, deﬁ ned and discussed in

Chapter 19:

CBA

S 60 Current stock price

X 50 Option exercise price

T 0.5000 Time to option exercise (in years)

r 8% Annual interest rate

Sigma 30% Riskiness of stock

n 20 Number of subdivisions of T

t = T/n

0.0250 <-- =B4/B7

Up, U 1.0486 <-- =EXP(B6*SQRT(B9))

Down, D 0.9537 <-- =EXP(-B6*SQRT(B9))

Interest rate, R 1.0020 <-- =EXP(B5*B9)

Binomial European call 12.8055 <-- =binomial_eur_call(B10,B11,B12,B2,B3,B7)

Black-Scholes call 12.8226 <-- =BSCall(B2,B3,B4,B5,B6)

BLACK-SCHOLES AND BINOMIAL PRICING

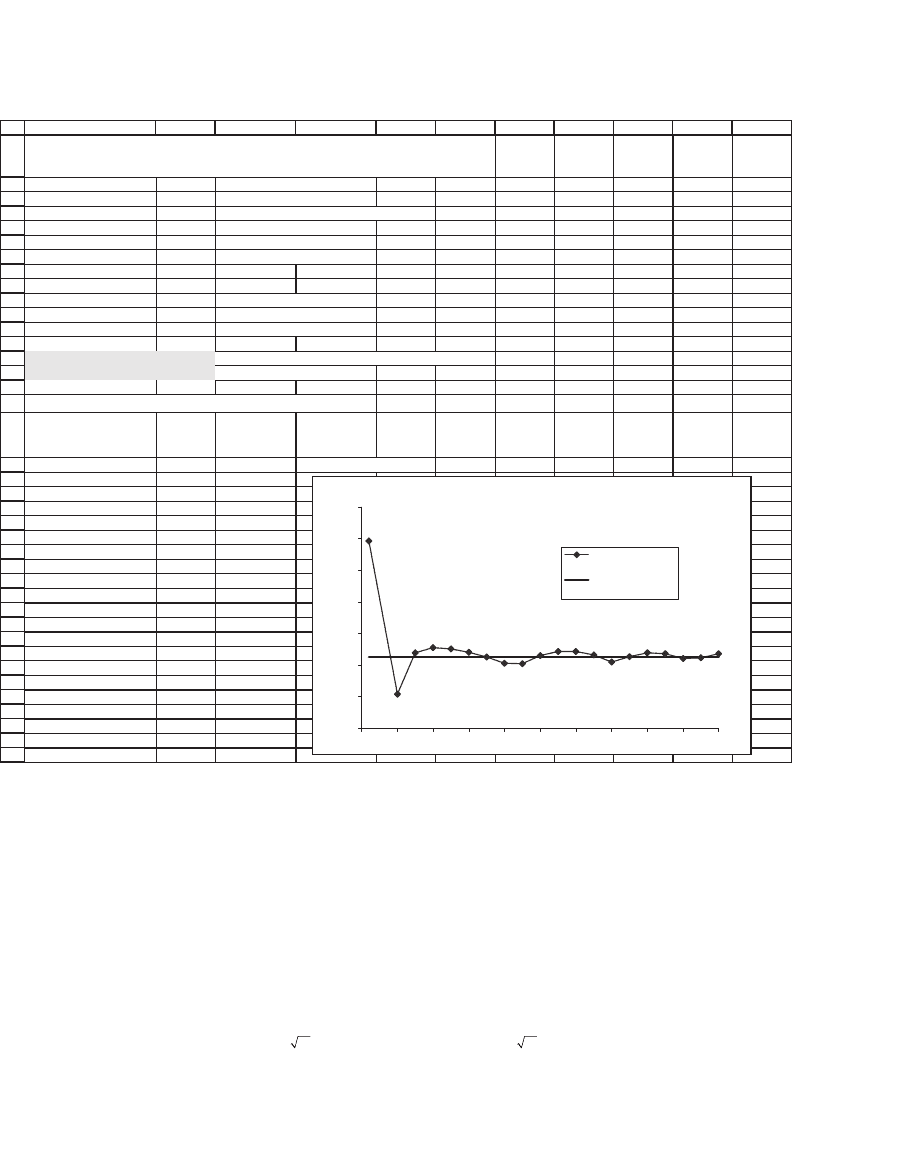
The binomial model gives a good approximation to the Black-Scholes

(cells B14:B15). As the n gets larger, this approximation gets better,

though the convergence to the Black-Scholes price is not smooth:

5. An alternative approximation that converges to a lognormal price process is given in

section 17.7.1. See also Omberg (1987), Hull (2006), and Benninga, Steinmetz, and

Stroughair (1993).

465 The Binomial Option-Pricing Model

17.7.1 An Alternative Approximation to the Lognormal

The approximation of the ﬁ rst part of this section is not the only appro x-

imation that works. If the stock price is lognormally distributed with

mean μ and standard deviation σ, we can also use the following

approximation:

ΔΔ ΔΔ

tTn Re

UeD e

tt tt

=+ = =+ =

+−

Up Down11

μσ μσ

Implementing this in our spreadsheet gives

ABCDEFGHIJ

S 60 Current stock price

X 50 Option exercise price

T 0.5000 Time to option exercise (in years)

r 8% Annual interest rate

Sigma 30% Riskiness of stock

n 20 Number of subdivisions of T

t = T/nΔ

0.0250 <-- =B4/B7

Up, U 1.0486 <-- =EXP(B6*SQRT(B9))

Down, D 0.9537 <-- =EXP(-B6*SQRT(B9))

Interest rate, R 1.0020 <-- =EXP(B5*B9)

Binomial European call 12.8055 <-- =binomial_eur_call(B10,B11,B12,B2,B3,B7)

Black-Scholes call 12.8226 <-- =BSCall(B2,B3,B4,B5,B6)

Data table: Binomial price vs Black-Scholes

n, number of

subdivisions

of T

Binomial

price

Black-

Scholes price

12.8055 12.8226 <-- Data table headers

10 12.8593 12.8226

50 12.8108 12.8226

75 12.8238 12.8226

100 12.8255 12.8226

125 12.8251 12.8226

150 12.8240 12.8226

175 12.8226 12.8226

200 12.8205 12.8226

225 12.8204 12.8226

250 12.8230 12.8226

275 12.8243 12.8226

300 12.8243 12.8226

325 12.8232 12.8226

350 12.8210 12.8226

375 12.8226 12.8226

400 12.8238 12.8226

425 12.8236 12.8226

450 12.8221 12.8226

475 12.8223 12.8226

500 12.8236 12.8226

BLACK-SCHOLES AND BINOMIAL PRICING:

CONVERGENCE

Convergence of Binomial to Black-Scholes

12.80

12.81

12.82

12.83

12.84

12.85

12.86

12.87

0 50 100 150 200 250 300 350 400 450 500

n, number of subdivisions of T

Binomial

price

Black-Scholes price

466 Chapter 17

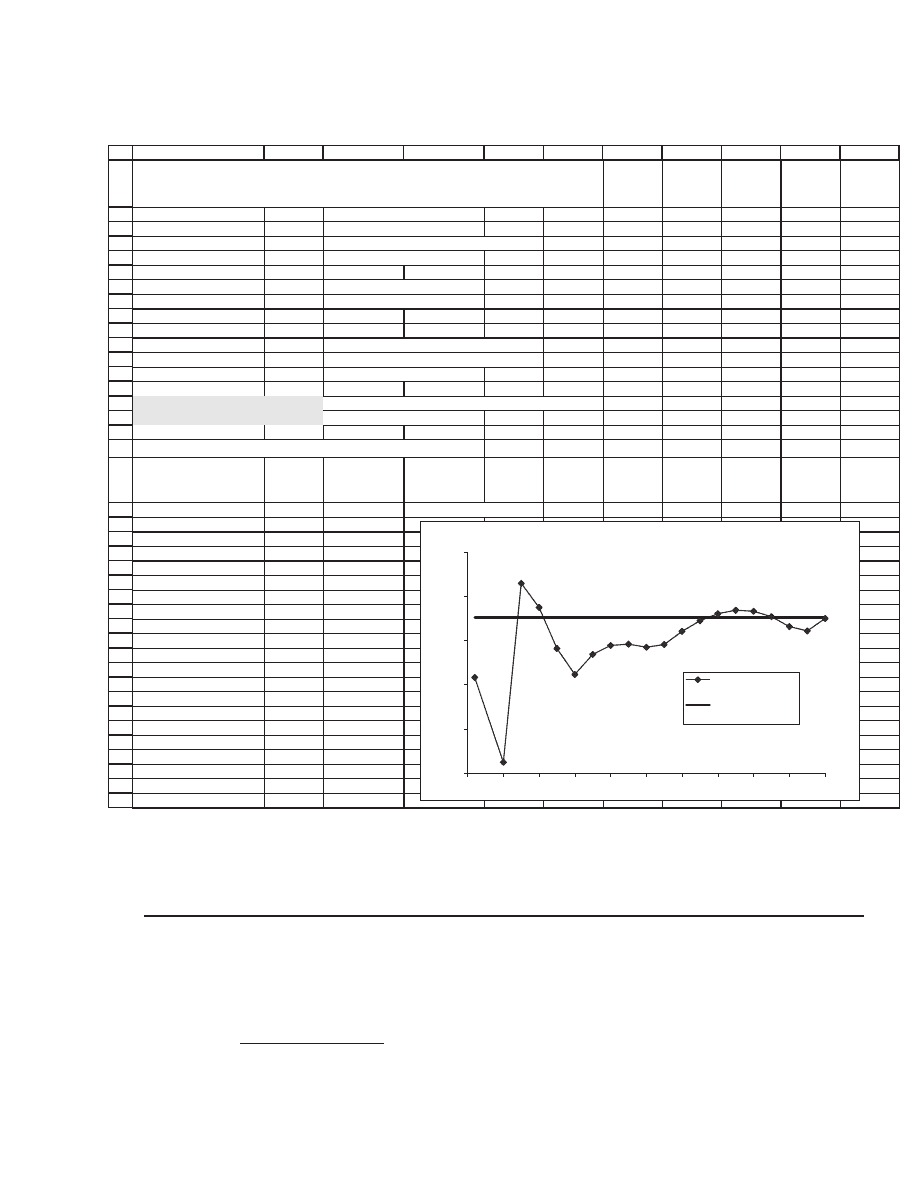
The convergence of this parameterization to Black-Scholes is some-

what less smooth, though the ultimate result is the same.

17.8 Using the Binomial Model to Price Employee Stock Options

An employee stock option (ESO) is a call option given by a company to

its employees as part of their remuneration package. Like all call options,

ABCDEFGHIJ

S 60 Current stock price

X 50 Option exercise price

T 0.5000 Time to option exercise (in years)

r 8% Annual interest rate

Mean return,

12%

Sigma,

30% Riskiness of stock

n 20 Number of subdivisions of T

t = T/n

0.0250 <-- =B4/B8

Up, U 1.0517 <-- =EXP(B6*B10+B7*SQRT(B10))

Down, D 0.9565 <-- =EXP(B6*B10-B7*SQRT(B10))

Interest rate, R 1.0020 <-- =EXP(B5*B10)

Binomial European call 12.8388 <-- =binomial_eur_call(B11,B12,B13,B2,B3,B8)

Black-Scholes call 12.8226 <-- =BSCall(B2,B3,B4,B5,B7)

Data table: Binomial price vs Black-Scholes

n, number of

subdivisions

of T

Binomial

price

Black-

Scholes price

12.8388 12.8226 <-- Data table headers

10 12.8158 12.8226

50 12.8062 12.8226

75 12.8264 12.8226

100 12.8237 12.8226

125 12.8191 12.8226

150 12.8162 12.8226

175 12.8184 12.8226

200 12.8194 12.8226

225 12.8196 12.8226

250 12.8192 12.8226

275 12.8195 12.8226

300 12.8210 12.8226

325 12.8222 12.8226

350 12.8230 12.8226

375 12.8234 12.8226

400 12.8233 12.8226

425 12.8227 12.8226

450 12.8216 12.8226

475 12.8211 12.8226

500 12.8225 12.8226

BLACK-SCHOLES AND BINOMIAL PRICING:

U=exp(

μΔ

*sqrt(

t) ), D=exp(

μΔ

*sqrt(

t) )

Convergence of Binomial to Black-Scholes

12.81

12.82

12.83

0 50 100 150 200 250 300 350 400 450 500

n, number of subdivisions of T

Binomial

price

Black-Scholes price

6. Note that both methods actually converge quite quickly—within several dozen steps

the binomial is within 0.01 of the Black-Scholes price.

7. This section has beneﬁ ted from discussions with Torben Voetmann of Cornerstone

Research and Zvi Wiener of Hebrew University, Jerusalem.

467 The Binomial Option-Pricing Model

the value of an ESO depends on the current price of the stock, the

option’s exercise price, and the time until exercise. However, ESOs

typically have several special conditions:

•

The option has a vesting period. During this period, the employee is

not allowed to exercise the option. An employee leaving the company

before the vesting period forfeits his option. In the model of this section

we assume that a typical employee of the company leaves at exit rate e

per year.

•

An employee leaving the company after the vesting period is forced to

exercise his option immediately.

•

For tax reasons, almost all ESOs have exercise prices equal to the stock

price on the date of issue.

In the model that follows, adapted from a paper by Hull and White

(2004), we assume that an employee will choose to exercise his option

when the price of the stock is greater than some multiple m of the ESOs

exercise price X. We ﬁ rst present the model’s implementation and results

and then discuss the VBA program that gives us these results:

CBA

S 50 Current stock price

X 50 Option exercise price

T 10.00 Time to option exercise (in years)

Vesting period (years) 3.00

Interest 5.00% Annual interest rate

Sigma 35% Riskiness of stock

Stock dividend rate 2.50% Annual dividend rate on stock

Exit rate, e 10.00%

Option exercise multiple, m 3.00

n 50 Number of subdivisions of one year

Employee stock option value 13.56 <-- =ESO(B2,B3,B4,B5,B6,B7,B8,B9,B10,B11)

Black-Scholes call 19.18 <-- =BSCall(B2*EXP(-B8*B4),B3,B4,B6,B7)

A BINOMIAL EMPLOYEE STOCK-OPTION-PRICING MODEL

Based on Hull and White (2004)

The ESO function in cell B13 depends on the 10 variables listed in

cells B2:B11. The screen for this function looks like this: