Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

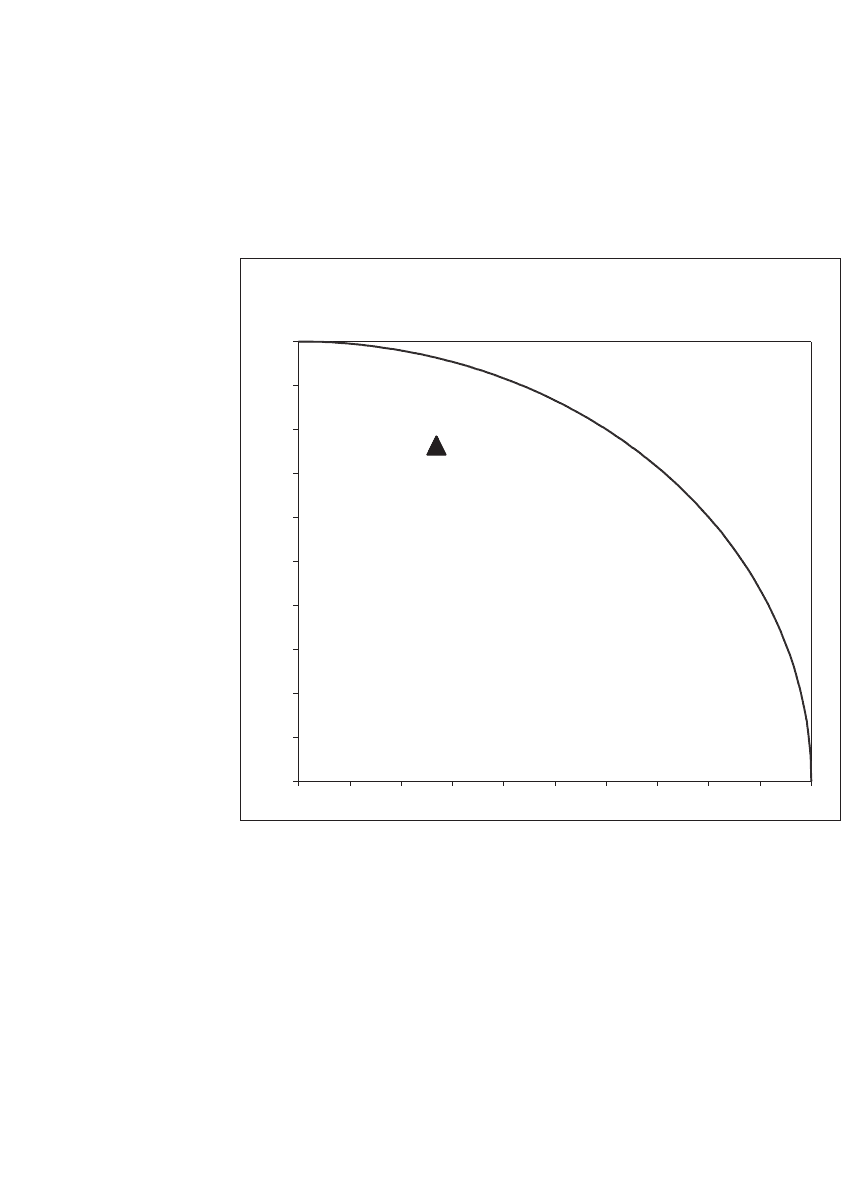
598 Chapter 22

By pressing F9 in the spreadsheet fm3_chapter22.xls, you can generate

different values of the random point. In some cases, the point will be

outside the unit circle:

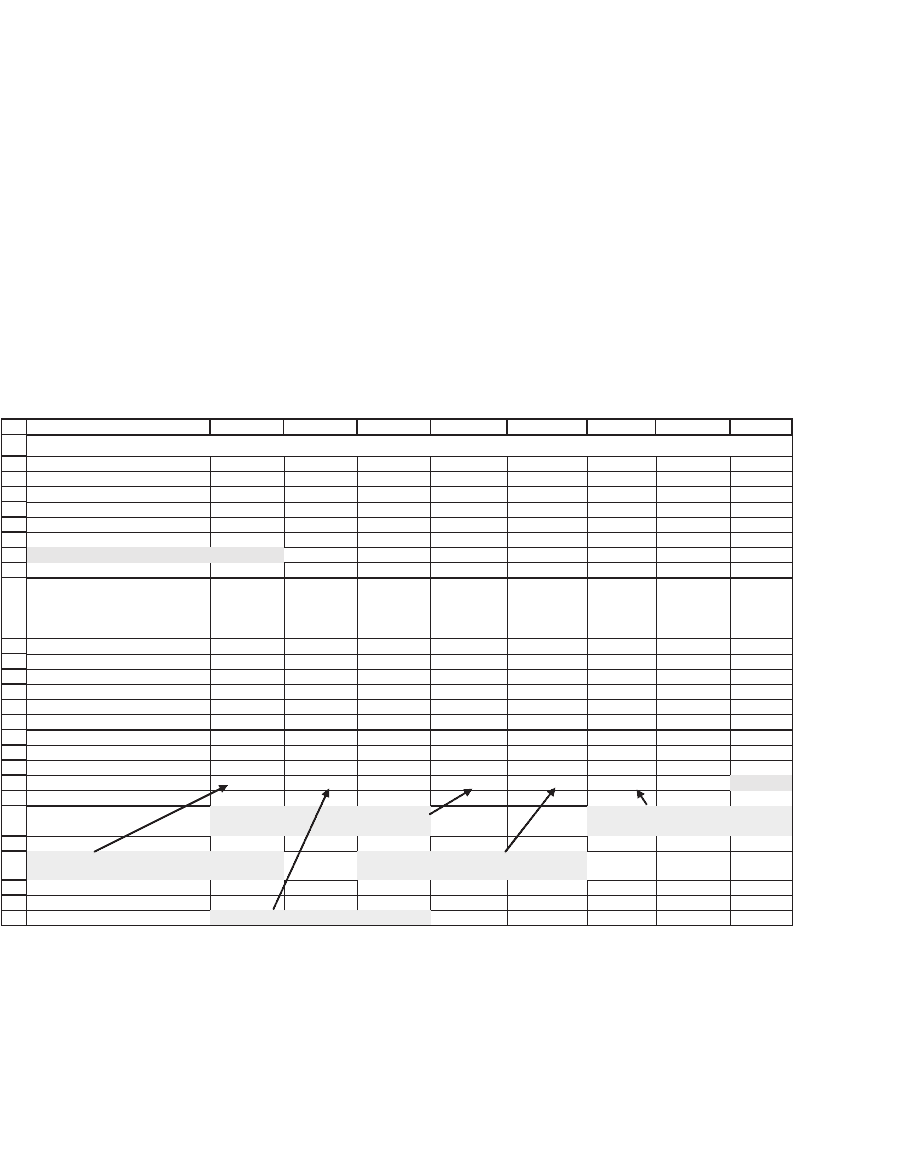
Quarter Unit Circle

Showing single random point {rand(),rand()}

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

The picture shows the quarter circle inscribed in the unit square and

a single random point, which happened to land inside the circle.

599 An Introduction to Monte Carlo Methods

We can easily do a calculation of the probability that the point will be

inside the circle:

•

The area of the whole unit circle is π

= π. Thus the area of the

quarter unit circle is π/4.

•

The random point—generated by {Rand(), Rand()}—is always inside

the unit square, whose area is 1.

•

Thus the probability of the random point being inside the unit circle is

Area unit circle

Area unit square

/4==

22.2.1 Monte Carlo Computation of p

If we count the relative number of points that fall inside the unit circle,

we should approximate π/4. Thus

Monte Carlo approximation Relative number points inside unit ci=∗4 rrcle

Number points inside unit circle

Total number of points

=∗4

Quarter Unit Circle

Showing single random point {rand(),rand()}

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

600 Chapter 22

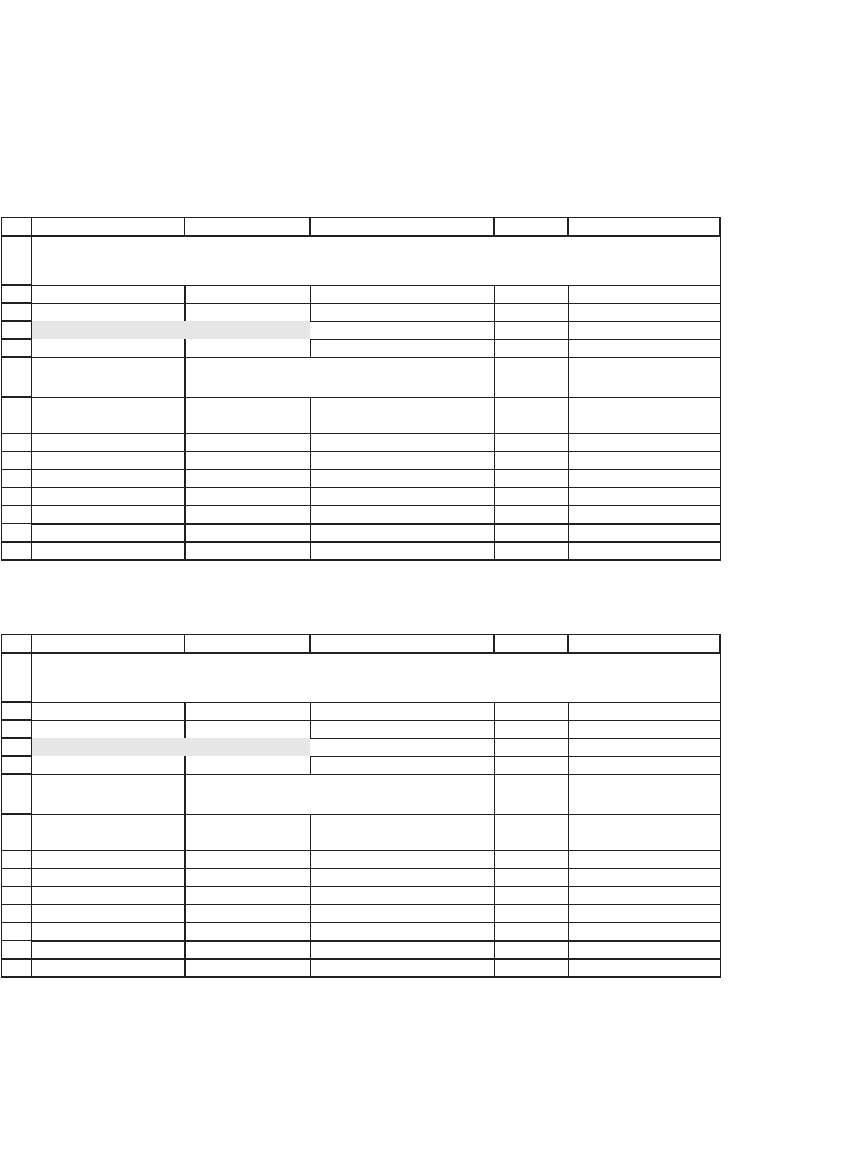
In the following spreadsheet we generate a list of random numbers

(columns B and C) and then use a Boolean function to test whether the

numbers are in or out of the unit circle. In row 8, for example, the

function = (B8^2 + C8^2 <= 1) returns TRUE if the sum of the squares of

B8 and C8 is less than or equal to 1 and 0 otherwise. In cells B2 and B3

we use Count to count the total number of points generated and CountIf

to determine the number of data points that fall inside the unit circle.

AB CDE

Number of data points 30 <-- =COUNT(A:A)

Inside circle 22 <-- =COUNTIF(D:D,TRUE)

Pi? 2.933333333 <-- =B3/B2*4

Experiment Random1 Random2

In unit

circle?

1 0.93377 0.14390 TRUE <-- =(B8^2+C8^2<=1)

2 0.28866 0.68112 TRUE

3 0.53592 0.60165 TRUE

4 0.38665 0.27952 TRUE

5 0.02396 0.62680 TRUE

6 0.98093 0.02753 TRUE

7 0.57770 0.34427 TRUE

8 0.58922 0.26317 TRUE

9 0.34752 0.77355 TRUE

10 0.96858 0.08618 TRUE

11 0.32394 0.66268 TRUE

12 0.04574 0.69957 TRUE

13 0.53216 0.99862 FALSE

14 0.88861 0.60825 FALSE

15 0.65561 0.39199 TRUE

16 0.79978 0.21315 TRUE

17 0.65605 0.99905 FALSE

18 0.23636 0.95164 TRUE

19 0.75541 0.17700 TRUE

20 0.29197 0.01494 TRUE

21 0.56781 0.40796 TRUE

22 0.25891 0.04545 TRUE

23 0.61585 0.88576 FALSE

24 0.32830 0.43645 TRUE

25 0.52969 0.47640 TRUE

26 0.60362 0.85435 FALSE

27 0.97880 0.20737 FALSE

28 0.62883 0.84034 FALSE

29 0.13787 0.66466 TRUE

30 0.98497 0.36433 FALSE

Each cell in these columns contains the Excel

function

=Rand()

COMPUTING PI USING MONTE CARLO METHODS

INITIAL EXPERIMENT

3. All the functions in this paragraph—Boolean functions, Count and CountIF—are dis-

cussed in Chapter 34.

601 An Introduction to Monte Carlo Methods

Each time we press F9 to recalculate the spreadsheet, we get different

values for the = Rand and hence a different Monte Carlo value for π.

Here is an example:

AB CDE

Number of data points 30 <-- =COUNT(A:A)

Inside circle 24 <-- =COUNTIF(D:D,TRUE)

Pi? 3.2 <-- =B3/B2*4

Experiment Random1 Random2

In unit

circle?

1 0.19891 0.21584 TRUE <-- =(B8^2+C8^2<=1)

2 0.60485 0.39918 TRUE

3 0.54090 0.50887 TRUE

4 0.01367 0.82935 TRUE

5 0.29872 0.02460 TRUE

6 0.98014 0.75186 FALSE

7 0.01627 0.34278 TRUE

Each cell in these columns contains the Excel

function =Rand()

COMPUTING PI USING MONTE CARLO METHODS

INITIAL EXPERIMENT

Pressing F9 again:

AB CDE

Number of data points 30 <-- =COUNT(A:A)

Inside circle 25 <-- =COUNTIF(D:D,TRUE)

Pi? 3.333333333 <-- =B3/B2*4

Experiment Random1 Random2

In unit

circle?

1 0.95610 0.35792 FALSE <-- =(B8^2+C8^2<=1)

2 0.65874 0.62250 TRUE

3 0.67164 0.23791 TRUE

4 0.81134 0.46254 TRUE

5 0.06633 0.01178 TRUE

6 0.70038 0.91783 FALSE

7 0.22334 0.19309 TRUE

Each cell in these columns contains the Excel

function =Rand()

COMPUTING PI USING MONTE CARLO METHODS

INITIAL EXPERIMENT

Now it’s clear that the values we get for π are experimental, but if we

applied this method for a lot of points we would get closer to the actual

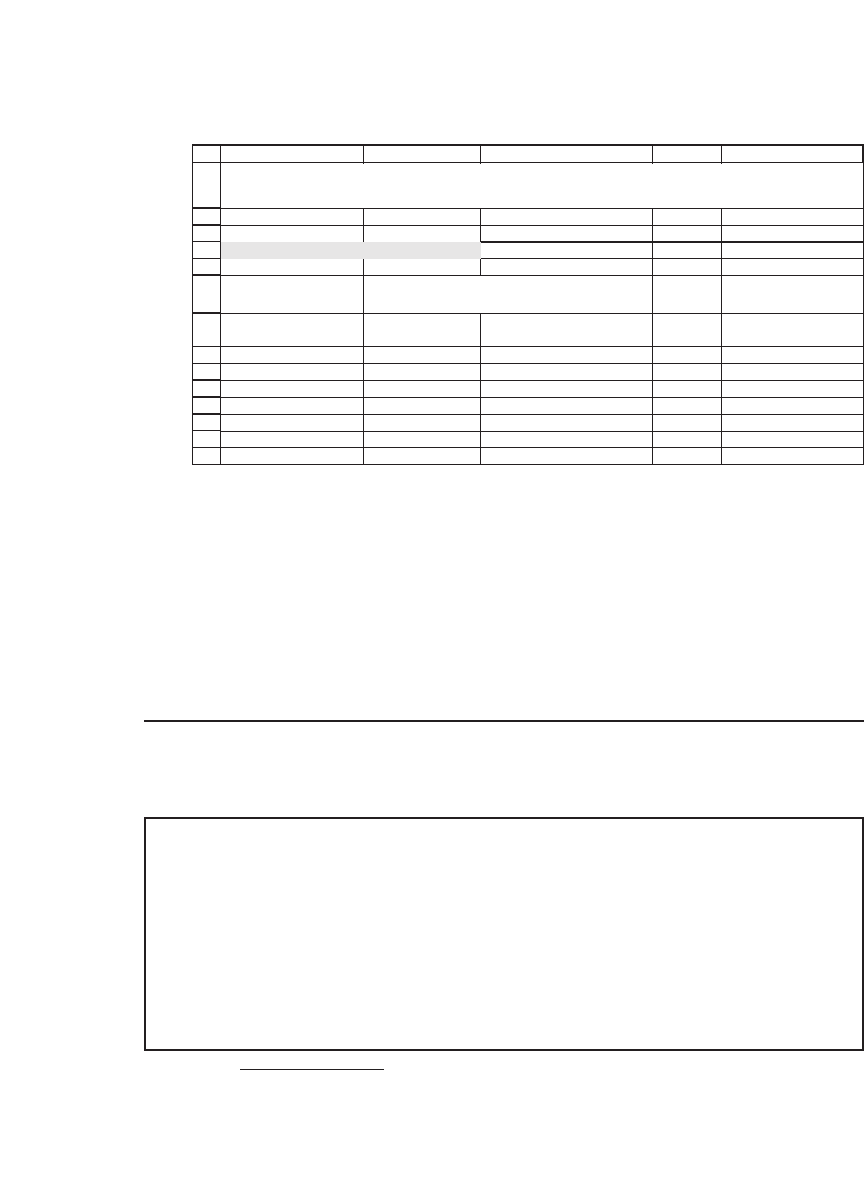
value of π. In the following example we ﬁ ll the whole of columns B and

C with random values:

602 Chapter 22

AB CDE

Number of data points 65,529 <-- =COUNT(A:A)

Inside circle 51,676 <-- =COUNTIF(D:D,TRUE)

Pi? 3.15438966 <-- =B3/B2*4

List Random1 Random2

In unit

circle?

1 0.47482 0.76071 TRUE <-- =(B8^2+C8^2<=1)

2 0.81690 0.85186 FALSE

3 0.21643 0.90968 TRUE

4 0.47165 0.50493 TRUE

5 0.89530 0.12251 TRUE

6 0.72624 0.37979 TRUE

7 0.60837 0.23161 TRUE

Each cell in these columns contains the Excel

function =Rand()

COMPUTING PI USING MONTE CARLO METHODS

All of columns B and C filled with random numbers

When we’ve ﬁ lled columns B and C with random numbers, you can see

that there are 65,529 random pairs. Pressing F9 gives much more accu-

rate values for π. A few more presses of F9 produced the following

Monte Carlo values for π:

3.150544034, 3.144256741, 3.139556532, 3.149872576, 3.138213615, 3.132780906

Using more data points makes our MC value for π more accurate, though

none of these values is very close to the actual value of π.

22.3 Writing a VBA Program

This Monte Carlo business requires some VBA. Here’s a program:

4. The actual value of π, correct to 50 digits, is 3.14159265358979323846264338327950288

41971693993751. One of the end-of-chapter problems shows you a quick way of com-

puting this value using several remarkable functions due to the Indian mathematician

Srinivasa Ramanujan (1887–1920).

Sub MonteCarlo()

n = Worksheets(“MC”).Range(“Number”)

Hits = 0

For Index = 1 To n

If Rnd ^ 2 + Rnd ^ 2 < 1 Then Hits = Hits + 1

Next Index

Range(“Estimate”) = 4 * Hits / n

End Sub

603 An Introduction to Monte Carlo Methods

The next spreadsheet shows this program and two other VBA pro-

grams. The program MonteCarloTimer computes both the StartTime

and the StopTime, so that we can compute the elapsed time for the

computations. You can see that 50 million iterations of the program took

33 seconds on the author’s Lenovo T60 laptop.

The program MonteCarloTimeRecord records each iteration of the

program on the screen. This VBA routine allows you to see how the

values of π in cell B3 develop. You can stop this or any VBA routine in

midstream by pressing [Ctrl] + [Break]. This macro is incredibly time

wasteful. It took us 103 seconds to run 5,000 iterations of the routine

(compare this ﬁ gure to running the 50 million iterations without the

screen updating).

DCBA E

Number of data points 50,000,000 <-- This cell called "Number"

Pi? 3.14158984 <-- This cell called "Estimate" Sub MonteCarlo()

n = Range("Number")

Hits = 0

StartTime 9:35:41 <-- This cell called "StartTime" For Index = 1 To n

StopTime 9:36:14 <-- This cell called "StopTime" If Rnd ^ 2 + Rnd ^ 2 < 1 Then Hits = Hits + 1

Elapsed 0:00:33 <-- =Stoptime-StartTime Next Index

Range("Estimate") = 4 * Hits / n

End Sub

Note

[Ctrl]+a runs the macro "MonteCarlo" Sub MonteCarloTime()

[Ctrl]+q runs the macro "MonteCarloTime" which also records the time 'Includes timer

n = Range("Number")

Range("StartTime") = Time

n = Range("Number")

Hits = 0

For Index = 1 To n

If Rnd ^ 2 + Rnd ^ 2 < 1 Then Hits = Hits + 1

Next Index

Range("Estimate") = 4 * Hits / n

Range("StopTime") = Time

End Sub

Sub MonteCarloTimeRecord()

'Records everything (takes a long time)

n = Range("Number")

Range("StartTime") = Time

n = Range("Number")

Hits = 0

For Index = 1 To n

Range("Number") = Index

If Rnd ^ 2 + Rnd ^ 2 < 1 Then Hits = Hits + 1

Range("Estimate") = 4 * Hits / Index

Range("StopTime") = Time

Next Index

End Sub

COMPUTING PI USING VBA

[Ctrl]+t runs the macro "MonteCarloTimeRecord" which records the

results as they are generated. For large number of points, this takes a

very long

time!

604 Chapter 22

22.4 Another Monte Carlo Problem: Investment and Retirement

The problem: You are 65 years old and you have $1,000,000. You are

trying to decide on a mix of investments: There is a riskless bond with

an annual return of 6 percent and a risky stock portfolio with an expected

log return of 12 percent and a standard deviation of return of 30 percent.

Your limitations: You want to take $150,000 out of the account every

year and have something left over at age 75.

To get a better handle on this situation, you plot out a spreadsheet:

ABCDEFGH

Current wealth 1,000,000

Risk-free rate 6%

Parameters of risky investment

Expected annual return 8%

Standard deviation of return 20%

Proportion invested in risky 70%

Annual drawdown 150,000

Year

Wealth at

beginning

of year

Invested in

risky

Invested in

bonds

Random

number,

normally

distributed

1+return on

risky

investment

Wealth at

end of year

Drawdown

Left at

end of 10

years

1 1,000,000 700,000 300,000 0.5450 1.2080 1,164,185 150,000

2 1,014,185 709,930 304,256 -0.1724 1.0466 1,066,069 150,000

3 916,069 641,248 274,821 -0.3924 1.0015 934,036 150,000

4 784,036 548,825 235,211 -0.3179 1.0166 807,665 150,000

5 657,665 460,366 197,300 -0.0825 1.0656 700,044 150,000

6 550,044 385,030 165,013 0.9566 1.3117 680,264 150,000

7 530,264 371,185 159,079 0.2509 1.1390 591,712 150,000

8 441,712 309,198 132,514 0.8803 1.2918 540,143 150,000

9 390,143 273,100 117,043 0.7485 1.2582 467,904 150,000

10 317,904 222,533 95,371 -1.4671 0.8078 281,032 150,000 131,032

Investment in risky asset =B20*$B$7

PLANNING YOUR RETIREMENT

=C20*F20+D20*EXP($B$3)

Normally-distributed random numbers

generated by =NORMSINV(RAND())

1+return on risky investment

=EXP($B$5+$B$6*E20)

Wealth at beginning of year =G19-H19

In this spreadsheet column B shows the wealth at the beginning of

every year. The wealth is divided between risky and riskless investments

according to the proportions in cell B7. The riskless investment earns a

continuously compounded return of 6 percent (meaning that $100

invested in the riskless investment grows to 100*e

at the end of the

year). The risky part of the investment grows by a factor of e

μ+σ*Z

605 An Introduction to Monte Carlo Methods

8%+20%*Z

, where Z is a random number that is normally distributed with

mean 0 and standard deviation 1. As explained in Chapter 30, one way

of generating these numbers is to use the Excel function NormSInv(Rand()).

With each press of F9, this function recomputes and produces another

normally distributed random number.

In the preceding simulation the investor has money left at the end of

the 10-year period. But it is clear that not every simulation will leave the

investor with spare cash at the end of year 10. A few presses of F9 to

recalculate the spreadsheet will produce something like this:

ABCDEFGH

Current wealth 1,000,000

Risk-free rate 6%

Parameters of risky investment

Expected annual return 8%

Standard deviation of return 20%

Proportion invested in risky 70%

Annual drawdown 150,000

Year

Wealth at

beginning

of year

Invested in

risky

Invested in

bonds

Random

number,

normally

distributed

1+return on

risky

investment

Wealth at

end of year

Drawdown

Left at

end of 10

years

1 1,000,000 700,000 300,000 -1.2459 0.8444 909,604 150,000

2 759,604 531,723 227,881 0.8373 1.2808 922,985 150,000

3 772,985 541,090 231,896 0.2468 1.1381 862,046 150,000

4 712,046 498,432 213,614 -0.1490 1.0515 750,918 150,000

5 600,918 420,643 180,276 -0.4724 0.9856 606,022 150,000

6 456,022 319,215 136,807 -1.1769 0.8561 418,543 150,000

7 268,543 187,980 80,563 1.3347 1.4147 351,485 150,000

8 201,485 141,040 60,446 -0.0254 1.0778 216,195 150,000

9 66,195 46,337 19,859 1.0822 1.3451 83,412 150,000

10 -66,588 -46,611 -19,976 -0.9549 0.8950 -62,927 150,000 -212,927

Investment in risky asset =B20*$B$7

PLANNING YOUR RETIREMENT

=C20*F20+D20*EXP($B$3)

Normally-distributed random numbers

generated by =NORMSINV(RAND())

1+return on risky investment

=EXP($B$5+$B$6*E20)

Wealth at beginning of year =G19-H19

What interests us is what percentage of the investment-consumption

paths will end with a positive remainder? We will use Monte Carlo tech-

niques to answer this question. But before we do, we consider a few

questions.

606 Chapter 22

22.4.1 Should We Apply the 70 Percent Rule Blindly?

In the preceding simulations we have split our investment between the

risky and the riskless investments mechanically. We have also continued

to draw down funds irrespective of whether there are funds in the

account.

In the following spreadsheet we correct this mechanical approach. We

assume that the investor deﬁ nes a “safety cushion.” The cushion in cell

B8 is 3, which is taken to mean that the annual drawdown is $150,000 if

the investor’s portfolio is worth at least 3

$150,000 at the end of the

year. If it is not, then the investor takes one-third of her portfolio value

as a drawdown:

ABCDEFGH

Current wealth 1,000,000

Risk-free rate 6%

Parameters of risky investment

Expected annual return 8%

Standard deviation of return 20%

Proportion invested in risky 70%

Safety cushion 3

Annual drawdown 150,000

Year

Wealth at

beginning

of year

Invested in

risky

Invested in

bonds

Random

number,

normally

distributed

1+return on

risky

investment

Wealth at

end of year

Drawdown

Left at end

of 10 years

1 1,000,000 700,000 300,000 -0.5471 0.9710 998,253 150,000

2 848,253 593,777 254,476 0.4716 1.1904 977,072 150,000

3 827,072 578,950 248,121 -0.8906 0.9065 788,306 150,000

4 638,306 446,814 191,492 0.4212 1.1785 729,907 150,000

5 579,907 405,935 173,972 0.9129 1.3003 712,560 150,000

6 562,560 393,792 168,768 0.0895 1.1029 613,500 150,000

7 463,500 324,450 139,050 -0.3590 1.0082 474,770 150,000

8 324,770 227,339 97,431 -0.9809 0.8903 305,860 101,953

9 203,906 142,734 61,172 -1.1469 0.8612 187,882 62,627

10 125,255 87,678 37,576 -0.2989 1.0204 129,369 43,123 86,246

Investment in risky asset =B21*$B$7

PLANNING YOUR RETIREMENT

Using a safety cushion of 3

Investor takes 150,000 if end-year wealth > 3*150,000, else takes end-year wealth/3

=C21*F21+D21*EXP($B$3)

Normally-distributed random numbers

generated by =NORMSINV(RAND())

1+return on risky investment

=EXP($B$5+$B$6*E21)

Wealth at beginning of year =G20-H20

Drawdown calculated as

=IF(G21>$B$8*$B$9,$B$9,G21/$B$8)

607 An Introduction to Monte Carlo Methods

Many rules like this can be devised. The problem here—phrased as

investment and payouts over retirement—is substantially the same as

that faced by any endowment manager struggling with the problem of

how to determine simultaneously the investment and the drawdown

policy of the endowment. As far as we know there is no analytical solu-

tion to this problem, though, as can be seen, it is not difﬁ cult to simulate

the problem.

22.5 A Monte Carlo Simulation of the Investment Problem

We will write a VBA function Successfulruns that resembles the earlier

problem (the one without the cushion). Given an investment policy, the

function Successfulruns determines the percentage of investment/draw-

down trajectories that will leave the retiree with positive wealth at the

end of his investment horizon.

Here is some output from this function:

DCBA

Current wealth 1,000,000

Risk-free rate 8%

Parameters of risky investment

Expected annual return 10%

Standard deviation of return 40%

Proportion invested in risky 40%

Annual drawdown 100,000

Years of investment 10

Runs 1,000

Successful runs 87.60% <-- =successfulruns(B2,B8,B3,B5,B6,B7,B9,B11)

HOW WELL DO WE DO?

PERCENTAGE OF POSITIVE OUTCOMES

The function result in cell B13 considers a retiree starting with $1

million, making an investment decision between a risk-free asset with

return 8 percent and a risky asset with stochastic returns μ = 10 percent

and σ = 40 percent, and desiring to draw down $100,000 per year. Simu-

lating 1,000 returns, we determine that in 87.6 percent of the cases the

investor will ﬁ nish with positive wealth at the end of 10 years.