Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

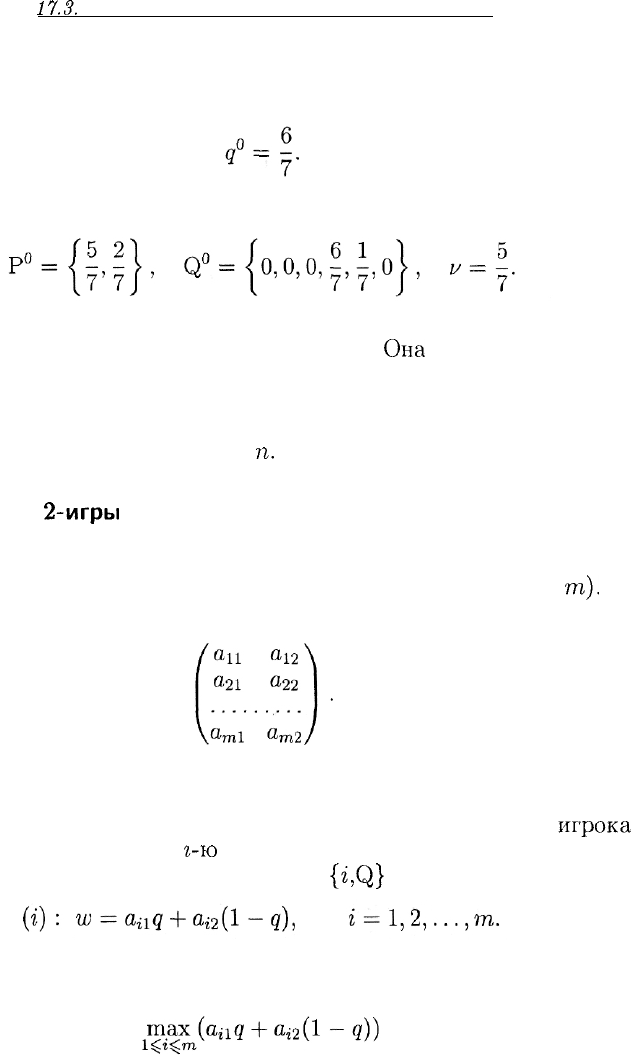
17.3.

МЕТОДЫ РЕШЕНИЯ МЛ ТРИЧНЫХ ИГР

3) получают (в обоих случаях), что

Полное решение игры имеет следующий вид:

Замечание. Ситуацию с наличием лишь двух конкурирующих стра-

тегий игрока А нельзя считать надуманной.

Она

возникает сравни-

тельно часто. Например, в случае, если нужно сравнить два образца

некоторого изделия (скажем, старого и модернизированного) с це-

лью выяснения возможности замены, это весьма удобно сделать при

помощи платежной матрицы 2 х

п.

17.3.2. m х

2-игры

Пусть теперь в матричной игре две чистые стратегии имеет игрок

Б, а число чистых стратегий у игрока А произвольно (равно

га).

Это означает, что платежная матрица такой игры имеет вид

является верхняя огибающая семейства прямых (2), соответствую-

щих чистым стратегиям игрока А (рис. 11).

331

Анализ такой игры во многом напоминает рассуждения, описан-

ные для игры 2 х п.

Пусть Q = {q, 1 — q} — произвольная смешанная стратегия

игрока

В. Если игрок А выбирает

г-ю

чистую стратегию, % = 1, 2,..., т, то

средний выигрыш игрока В в ситуации

{i,Q}

будет равным

Зависимость этого выигрыша от переменной q описывается прямой.

Графиком функции

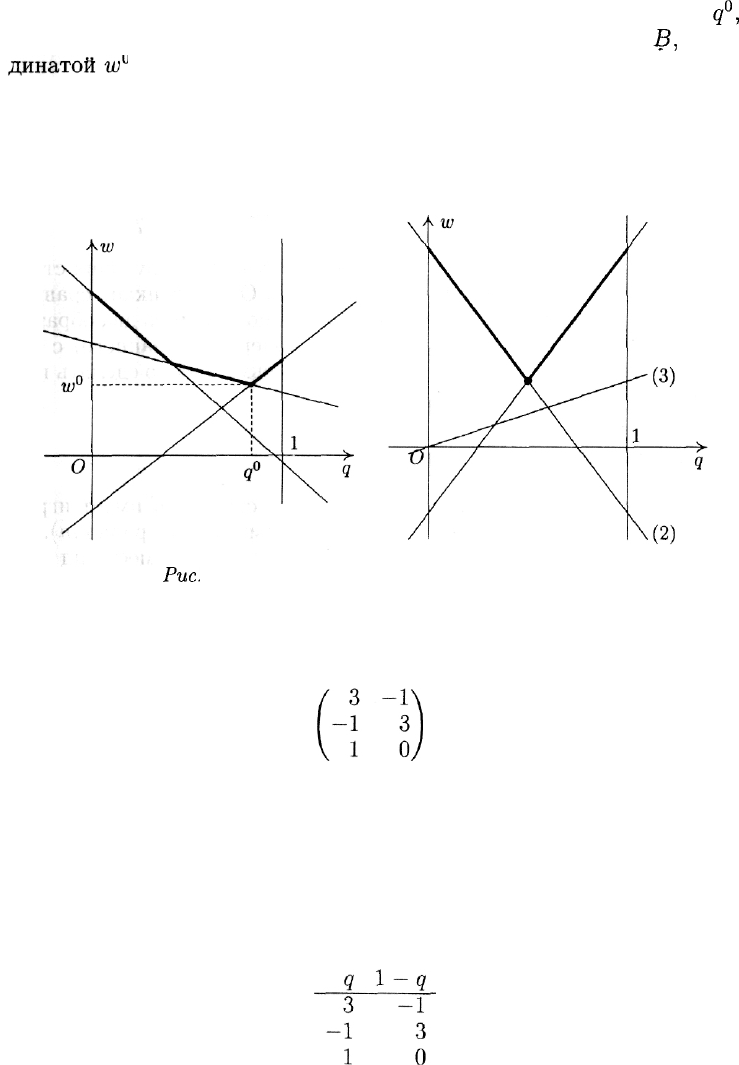
ГЛАВА 17. МАТРИЧНЫЕ ИГРЫ

Абсциссой нижней точки полученной ломаной будет значение

q°,

определяющее оптимальную смешанную стратегию игрока

В,

а ор-

цена игры.

Замечание. Отыскание оптимальной смешанной стратегии игрока А

проводится по той же схеме, которая позволяет находить оптималь-

ную смешанную стратегию игрока В в игре 2 х п.

(1)

Рис.

11 Рис. 12

Рассмотрим конкретный пример.

Пример 5. 3 х 2-игра задана матрицей

Решение.

1-й шаг. Анализ игры на наличие седловой точки.

Нижняя цена игры равна 0, верхняя — равна 3. Седловой точки

нет. Решение игры нужно искать в смешанных стратегиях.

2-й шаг. Вычисление средних выигрышей игрока В (проводится

при условии, что игрок А выбирает только чистые стратегии).

Из таблицы

332

17.3.

МЕТОДЫ РЕШЕНИЯ

MAТРИЧНЫХ

ИГР

получаем:

3-й шаг. Построение верхней огибающей.

Построим на координатной плоскости (q,

все три прямые, а

затем и их верхнюю огибающую (рис. 12).

4-й шаг. Отыскание цены игры и

оптимальной

смешанной стра-

тегии игрока В.

Нижняя точка верхней огибающей является точкой пересечения

прямых (1) и (2). Решая систему уравнений

получаем

5-й шаг. Отыскание оптимальной смешанной стратегии игро-

ка А.

Полагая

приравниваем средние выигрыши игрока А, соответствующие чи-

стым стратегиям игрока

В:

и находим

р°

= 1/2.

Таким образом, цена игры и оптимальные смешанные стратегии

игроков А

В соответственно равны:

17.3.3. т х п-игры

В принципе решение любой матричной игры сводится к решению

стандартной задачи линейного программирования и тем самым мо-

жет быть найдено методами линейного программирования. При этом

требуемый объем вычислений напрямую зависит от числа чистых

333

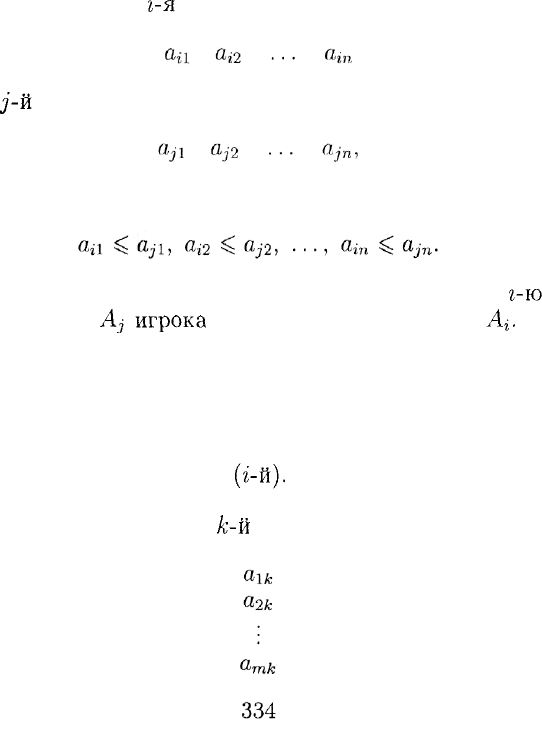
ГЛАВА 17. МАТРИЧНЫЕ ИГРЫ

стратегий игроков (растет с его увеличением и, значит, с увеличени-

ем размеров матрицы игры). Поэтому любые приемы предваритель-

ного анализа игры, позволяющие уменьшать размеры ее платежной

матрицы или еще как-то упрощать эту матрицу, не нанося ущерба

решению, играют на практике весьма важную роль.

Правило доминирования. В целом ряде случаев анализ платежной

матрицы обнаруживает, что некоторые чистые стратегии не могут

внести никакого вклада в искомые оптимальные смешанные страте-

гии. Отбрасывание подобных стратегий позволяет заменить перво-

начальную матрицу на матрицу выигрышей меньших размеров.

Опишем одну из таких возможностей более подробно.

Сравнение строк и столбцов матрицы

Будем говорить, что

г-я

строка матрицы А

не больше

j'-й

строки этой матрицы

если одновременно выполнены следующие п неравенств:

При этом говорят также, что j-я строка доминирует

г-ю

строку

или что стратегия

игрока

А доминирует стратегию

А%.

Замечание. Игрок А поступит разумно, если будет избегать страте-

гий, которым в матрице игры отвечают доминируемые строки.

Если в матрице А одна из строк (j-я) доминирует другую строку

(г-ю), то число строк в матрице А можно уменьшить путем отбра-

сывания доминируемой строки

(г-й).

Далее, будем говорить, что

к-Ш

столбец матрицы А

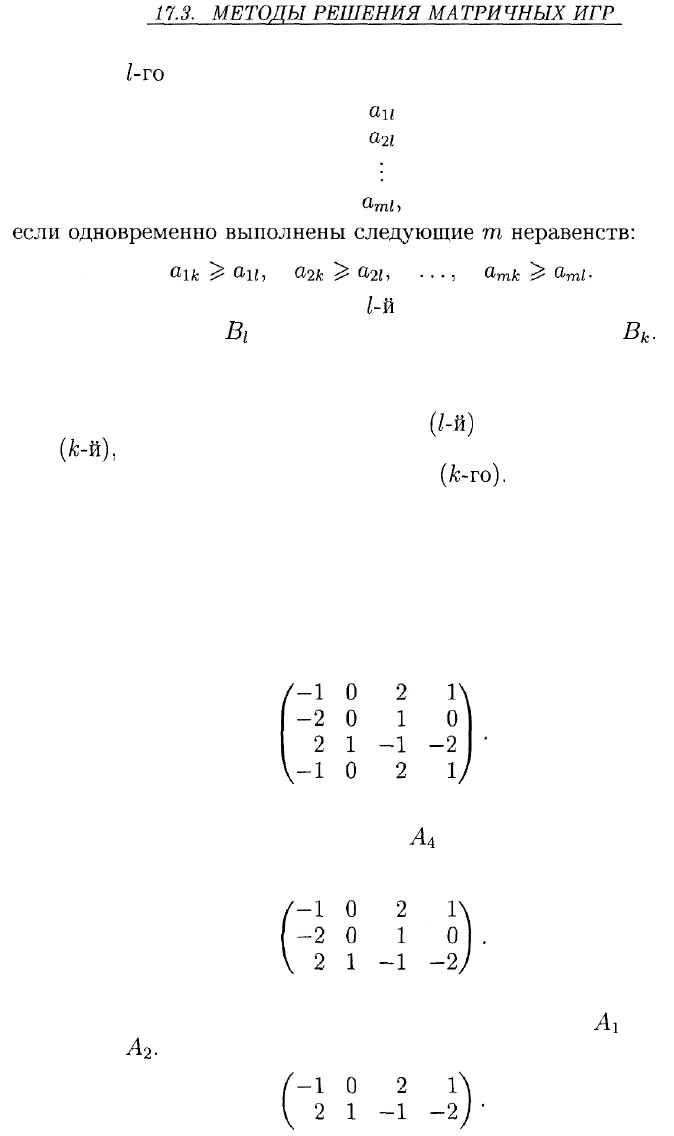
не меньше

1-го

столбца этой матрицы

Сравнивая поэлементно 1-ю и 2-ю строки, замечаем, что 1-я стро-

ка доминирует 2-ю строку, или, что то же, стратегия

А\

доминирует

стратегию

Это вновь позволяет уменьшить число строк матрицы:

Сравнивая строки матрицы, видим, что 1-я строка совпадает с 4-й

строкой, или, что то же, стратегия

А\

дублирует стратегию А\.

Тем самым одну из этих строк можно вычеркнуть, не нанося

ущерба решению:

При этом говорят также, что

1-й

столбец доминирует к-й столбец

или что стратегия

В[

игрока В доминирует стратегию

Замечание. Игрок В поступит разумно, если будет избегать страте-

гий, которым в матрице игры отвечают доминируемые столбцы.

Если в матрице А один из столбцов

(1-й)

доминирует другой стол-

бец

(к-й),

то число столбцов в матрице А можно уменьшить путем

отбрасывания доминируемого столбца

(к-го).

Важное замечание. Оптимальные смешанные стратегии в игре с

матрицей, полученной усечением исходной за счет доминируемых

строк и столбцов, дадут оптимальное решение в исходной игре: до-

минируемые чистые стратегии игроков в смешении не участвуют —

соответствующие им вероятности следует взять равными нулю.

Пример 6. Рассмотрим игру с матрицей

ГЛАВА

П.

МАТРИЧНЫЕ ИГРЫ

(см. пример 6).

336

Поэтому цена игры с матрицей С легко вычисляется:

связаны равенством

Элементы матриц

Замечание. При отбрасывании доминируемых строк и столбцов не-

которые из оптимальных стратегий могут быть потеряны. Однако

цена игры не изменится, и по усеченной матрице может быть найде-

на хотя бы одна пара оптимальных смешанных стратегий.

Аффинное правило. При поиске решения матричных игр часто ока-

зывается полезным следующее свойство.

Оптимальные стратегии у матричных игр, элементы матриц

А и С которых связаны равенствами

Возвращаясь к исходной 4х4-игре, получаем окончательный ответ:

Решая эту

2хЗ-игру

графическим методом, находим ее решение —

цену игры и оптимальные смешанные стратегии игроков А и

В:

Замечая, что 4-й столбец полученной матрицы доминирует ее 3-й

столбец, приходим к игре с 2 х 3-матрицей:

17.3. МЕТОДЫ РЕШЕНИЯ МАТРИЧНЫХ ИГР

Основные этапы поиска решения матричной игры. 1-й

этап

— про-

верка наличия (или отсутствия) равновесия в чистых стратегиях

(при наличии равновесной ситуации указываются соответствующие

оптимальные стратегии игроков и цена игры).

2-й этап — поиск доминирующих стратегий (в случае успеха это-

го поиска — отбрасывание доминируемых строк и столбцов в исход-

ной матрице игры).

3-й

этап—

замена игры на ее смешанное расширение и отыскание

оптимальных смешанных стратегий и цены игры.

17.3.4. Итерационный метод решения матричных игр

Опишем метод отыскания решения матричной игры — цены игры и

оптимальных смешанных стратегий, в известной степени верно от-

ражающий некоторую реальную ситуацию накопления опыта посте-

пенной выработки игроками хороших стратегий в результате многих

повторений конфликтных ситуаций. Основная идея этого метода за-

ключается в том, чтобы мысленно как бы смоделировать реальное

практическое "обучение" игроков в ходе самой игры, когда каждый

из них на опыте прощупывает способ поведения противника и стара-

ется отвечать на него наиболее выгодным для себя образом. Иными

словами, всякий раз при возобновлении игры игрок выбирает наибо-

лее выгодную для себя стратегию, опираясь на предыдущий выбор

противника.

Проиллюстрируем этот метод на примере игры, заданной мат-

рицей

(2 0

-У

(здесь

maxrnin

= 0,

minmax

= 2, следовательно, седловой точки

нет).

Опишем правила выбора ходов игроками, предположив для опре-

деленности, что начинает игрок

А:

ход игрока А — стратегия

А\

- (2 0 3);

игрок В выбирает свою стратегию так, чтобы выигрыш игрока А

был минимален (отмечен выше полужирным шрифтом):

ход игрока В — стратегия

- (0 3);

игрок А выбирает свою стратегию так, чтобы его выигрыш при

стратегии

игрока В был максимален (отмечен выше полужирным

шрифтом):

337

ГЛАВА 17. МАТРИЧНЫЕ ИГРЫ

ход игрока А — стратегия

3 — 3);

игрок В выбирает свою стратегию так, чтобы "накопленный" вы-

игрыш игрока А при стратегиях А\ и

был минимален:

ход игрока В — стратегия

- (3 — 3);

игрок

выбирает свою стратегию так, чтобы его "накопленный"

выигрыш при стратегиях

игрока В,

(О 3) + (3 -3) = (3 0),

был максимален:

ход игрока А — стратегия А\ - (2 0 3);

игрок В выбирает свою стратегию так, чтобы "накопленный" вы-

игрыш игрока А при стратегиях А\,

(3 3 0) + (2 0 3) = (5 3 3),

был минимален:

ход игрока В — стратегия

- (0 3);

и т. д.

Разобьем последовательные ходы игроков А и В на пары

(ход

игрока

А,

ход игрока В)

и запишем результаты в таблице:

требующей

некоторых

пояснений.

338

17.3.

МЕТОДЫ РЕШЕНИЯ

MAТРИЧНЫХ

ИГР

Описание таблицы

1-й столбец — номер n-го шага (пары последовательных ходов

игроков А

В),

2-й столбец — номер

г-й

стратегии, выбранной игроком

А,

3-й столбец — "накопленный" суммарный выигрыш игрока А за

первые п шагов при стратегии

В\

игрока В,

4-й столбец — "накопленный" суммарный выигрыш игрока А за

первые п шагов при стратегии

B<i

игрока В,

5-й столбец — "накопленный" суммарный выигрыш игрока А за

первые п шагов при стратегии

игрока В

(минимальный из этих выигрышей выделяется полужирным

шрифтом),

6-й столбец — минимальный средний выигрыш игрока А, равный

минимальному накопленному им выигрышу за первые п шагов, де-

ленному на число этих шагов,

7-й столбец — номер

стратегии, выбранной игроком В,

8-й столбец — "накопленный" суммарный выигрыш игрока А за

первые п шагов при стратегии А\,

9-й столбец — "накопленный" суммарный выигрыш игрока А за

первые п шагов при стратегии

А2

(максимальный из этих выигрышей выделяется полужирным

шрифтом),

10-й столбец — максимальный средний выигрыш игрока А, рав-

ный максимальному накопленному им выигрышу за первые п шагов,

деленному на число этих шагов,

11-й столбец — среднее арифметическое минимального среднего

выигрыша и максимального среднего выигрыша игрока А.

Цена игры определяется приближенно по окончании любого из

шагов. Например, за приближенную цену игры можно взять среднее

арифметическое

^(п),

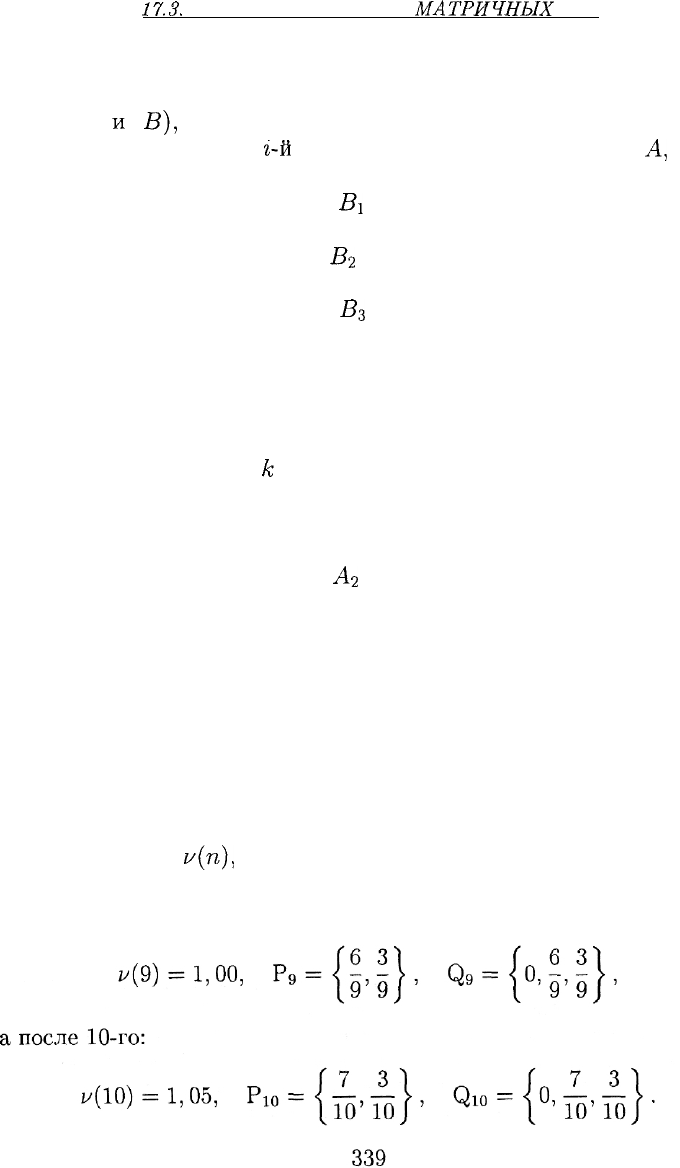
полученное на n-м шаге.

Смешанные стратегии противников определяются частотами по-

явления чистых стратегий. Например, после 9-го шага имеем:

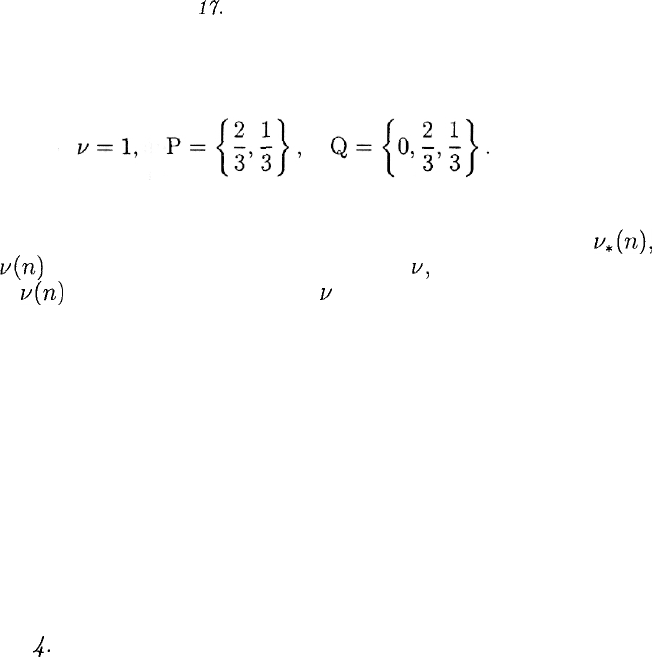
ГЛАВА

П.

МАТРИЧНЫЕ ИГРЫ

Так как эта игра легко решается графически, полезно сравнить

полученные результаты с точными:

Сделаем несколько замечаний.

Замечание 1. При увеличении числа шагов все три величины

f*(n),

v*(n) и

i/(n)

будут приближаться к цене игры

и,

но среднее арифме-

тическое

v{n)

будет приближаться к

сравнительно быстрее.

Замечание 2. Хотя сходимость итераций весьма медленна, тем не

менее даже такой небольшой расчет всегда дает возможность нахо-

дить ориентировочное значение цены игры и доли чистых стратегий.

Замечание 3. Сравнительно медленную скорость сходимости можно

объяснить целым рядом причин. Укажем одну из них, психологи-

чески наиболее интересную. Если, к примеру, игрок А уже нашел

оптимальную смешанную стратегию, то он не склонен останавли-

ваться на ней — он продолжит попытки выиграть у противника В

побольше, особенно если последний еще не достиг оптимальной сме-

шанной стратегии. Тем самым игрок А может невольно ухудшить

свое положение.

Замечание

Отметим два основных преимущества описанного ме-

тода:

1) итерационный метод прост и одновременно универсален (при

его помощи можно легко найти приближенное решение любой ма-

тричной игры),

2) объем и сложность вычислений сравнительно слабо растут по

мере увеличения числа стратегий игроков (размеров матрицы игры).

17.4. Некоторые задачи, сводимые

к матричным играм

В чистом виде антагонистические конфликты встречаются редко

(разве только в боевых действиях и в спортивных состязаниях). Од-

нако довольно часто конфликты, в которых интересы сторон проти-

воположны, при допущении, что множество способов действия сто-

рон конечно, можно моделировать матричными играми.

Рассмотрим несколько конкретных ситуаций.

340