Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

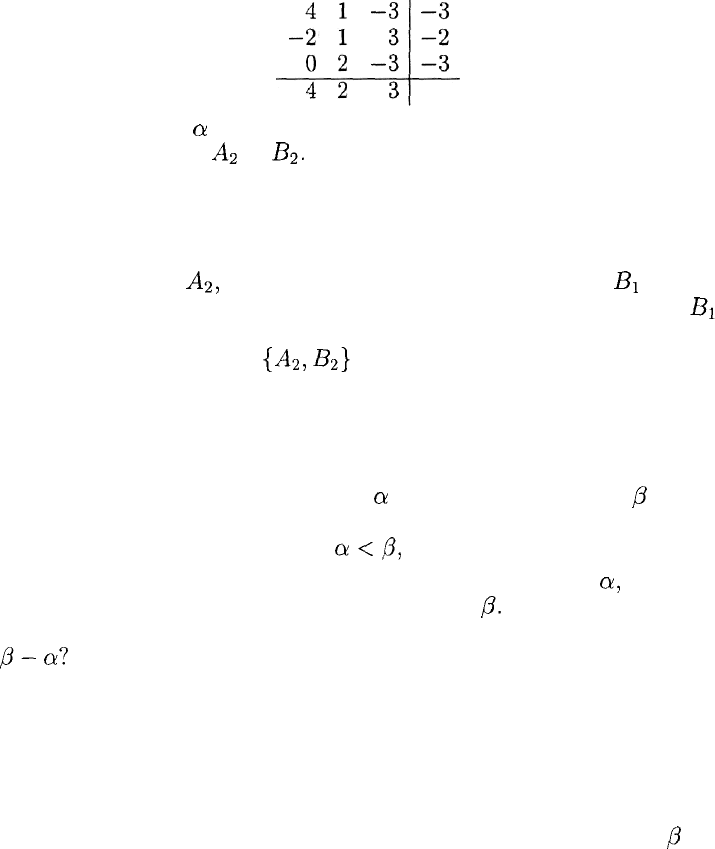
17.2. СМЕШАННЫЕ СТРАТЕГИИ

Применив предложенный алгоритм

находим нижнюю

= — 2 и верхнюю /3 = 2 цену игры и соответству-

ющие им стратегии

Аг

1?2-

Нетрудно убедиться в том, что, пока игроки придерживаются этих

стратегий, средний выигрыш при многократном повторении игры бу-

дет равен 1. Он больше нижней цены игры, но меньше верхней цены.

Однако если игроку В станет известно, что игрок А придержи-

вается стратегии

А%,

он немедленно ответит стратегией

В\

и сведет

его выигрыш к проигрышу —2. В свою очередь, на стратегию

В\

игрока А имеется ответная стратегия А\, дающая ему выигрыш 4.

Тем самым ситуация

{^2,-62}

равновесной не является.

17.2. Смешанные стратегии

В случае когда нижняя цена игры

а.

и верхняя цена игры

не сов-

падают,

а<Р,

игрок А может обеспечить себе выигрыш, не меньший

а,

а игрок В

имеет возможность не дать ему больше, чем

/3.

Возникает вопрос: а как разделить между игроками разность

Р-оР.

Предыдущие построения на этот вопрос ответа не дают — тесны

рамки возможных действий игроков.

Поэтому довольно ясно, что механизм, обеспечивающий получе-

ние каждым из игроков как можно большей доли этой разности,

следует искать в определенном расширении стратегических возмож-

ностей, имеющихся у игроков изначально.

Оказывается, что компромиссного распределения разности

— а,

между игроками и уверенного получения каждым игроком своей до-

ли при многократном повторении игры можно достичь путем слу-

чайного применения ими своих первоначальных, чистых стратегий.

Такие действия,

во-первых, обеспечивают наибольшую скрытность выбора страте-

гии (результат выбора не может стать известным противнику, пос-

кольку он неизвестен самому игроку),

321

ГЛАВА 17. МАТРИЧНЫЕ ИГРЫ

во-вторых, при разумном построении механизма случайного вы-

бора стратегий последние оказываются оптимальными.

Случайная величина, значениями которой являются стратегии

игрока, называется его смешанной стратегией.

Тем самым задание смешанной стратегии игрока состоит в указа-

нии тех вероятностей, с которыми выбираются его первоначальные

стратегии.

Рассмотрим произвольную га х n-игру, заданную т х п-матрицей

А = (a

Так как игрок А имеет т чистых стратегий, то его смешанная

стратегия может быть описана набором m неотрицательных чисел:

Р\ ^ 0,

^ 0, ...,

О,

сумма которых равна 1,

Смешанная стратегия второго игрока В, имеющего п чистых стра-

тегий, описывается набором п неотрицательных чисел:

0, . . . ,

О,

сумма которых равна 1,

Замечание. Каждая чистая стратегия является частным случаем

смешанной стратегии: например, чистая стратегия

Л,

является сме-

шанной стратегией, описываемой набором чисел

рг>

•••>

Рт,

котором

Подчеркнем, что для соблюдения секретности каждый из игроков

применяет свои стратегии независимо от другого игрока.

Таким образом, задав два набора:

мы оказываемся в ситуации в смешанных стратегиях.

322

17.2. СМЕШАННЫЕ СТРАТЕГИИ

В этих условиях каждая обычная ситуация (в чистых стратегиях)

{Ai,

Bk}

по определению является случайным событием и ввиду не-

зависимости Р и Q реализуется с вероятностью

р^.

Поскольку в

этой ситуации игрок А получает выигрыш

а^,

то математическое

ожидание выигрыша в условиях ситуации в смешанных стратегиях

{Р, Q} равно

Это число и принимается за средний выигрыш игрока А в ситуации

в смешанных стратегиях {P,Q}.

Стратегии

называются оптимальными смешанными стратегиями игроков А

и В соответственно, если выполнено следующее соотношение:

определяемая последней формулой, называется ценой игры.

Набор

(P°,Q°,f),

состоящий из оптимальных смешанных страте-

гий игроков А и В и цены игры, называется решением матричной

игры.

Естественно, возникают два ключевых вопроса:

1) какие матричные игры имеют решение в смешанных стратеги-

2) как находить решение матричной игры, если оно существует?

Ответы на эти вопросы дают следующие две теоремы.

323

ях?

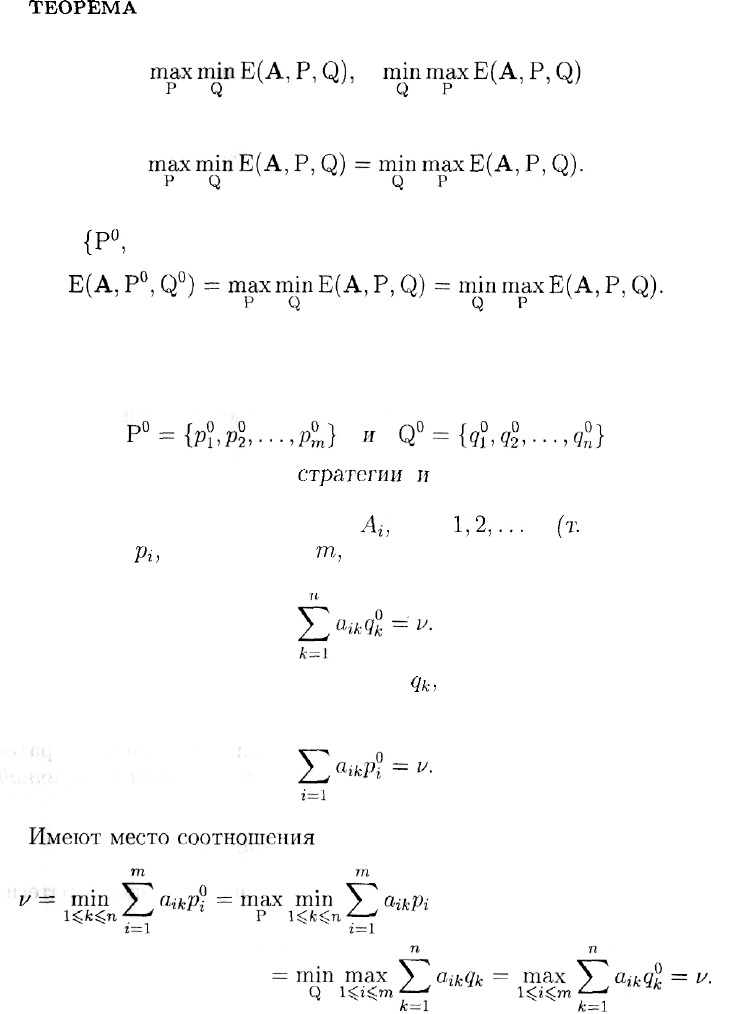
ГЛАВА 17. МАТРИЧНЫЕ ИГРЫ

Основная теорема теории матричных игр

ТЕОРЕМА

1 (Дж. фон Нейман). Для матричной игры с любой

матрицей А величины

существуют и равны между собой:

Более того, существует хотя бы одна ситуация в смешанных стра-

тегиях

{Р°,

}, для которой выполняется соотношение

Основные свойства оптимальных смешанных стратегий

ТЕОРЕМА 2. Пусть

— оптимальные смешанные

стратегии

v -- цена игры.

Оптимальная смешанная стратегия Р° игрока А смешивается

только из тех чистых стратегий

А\,

i =

1,2,...

(т.

е. только те

вероятности

Pi,

i = 1,2,...,

могут быть отличны от нуля), для

которых

Аналогично, только те вероятности

k — 1, 2,. . ., п, могут быть

отличны от нуля, для которых

324

17.3.

МЕТОДЫ РЕШЕНИЯ

MAТРИЧНЫХ

ИГР

В этом последнем скоплении равенств, по существу, и лежат исто-

ки, питающие методы построения решений матричных игр.

Опишем некоторые из них.

Опишем общую схему, приводящую к искомому результату.

Максимум функции

проще всего найти, построив ее график.

Для этого поступают следующим образом.

Предположим, что игрок А выбрал смешанную стратегию

Р = {р, 1 — р}, а игрок В — к-ю чистую стратегию,

— 1, 2, ...,

п. Тогда средний выигрыш игрока А в ситуации {Р, к} оказывается

равным

На плоскости

(р,

го) уравнение (к) описывает прямую. Тем самым

каждой чистой стратегии игрока В на этой плоскости соответствует

своя прямая.

325

17.3. Методы решения матричных игр

Наши рассмотрения мы начнем с матричных игр, в которых число

стратегий хотя бы одного из игроков равно двум.

Для построения решений 2 х п- и

х 2-игр существует эффектив-

ный метод, основанный на простых геометрических соображениях.

Этот метод называют графическим.

17.3.1. 2 х п-игры

Пусть

— платежная матрица 2 х п-игры.

Согласно теореме о двойном описании игры (теорема 2), нахожде-

ние цены игры и оптимального значения

р°

для игрока А равносиль-

но решению уравнения

ГЛАВА 17. МАТРИЧНЫЕ ИГРЫ

Поэтому сначала на плоскости (р,

последовательно и аккурат-

но рисуются все прямые

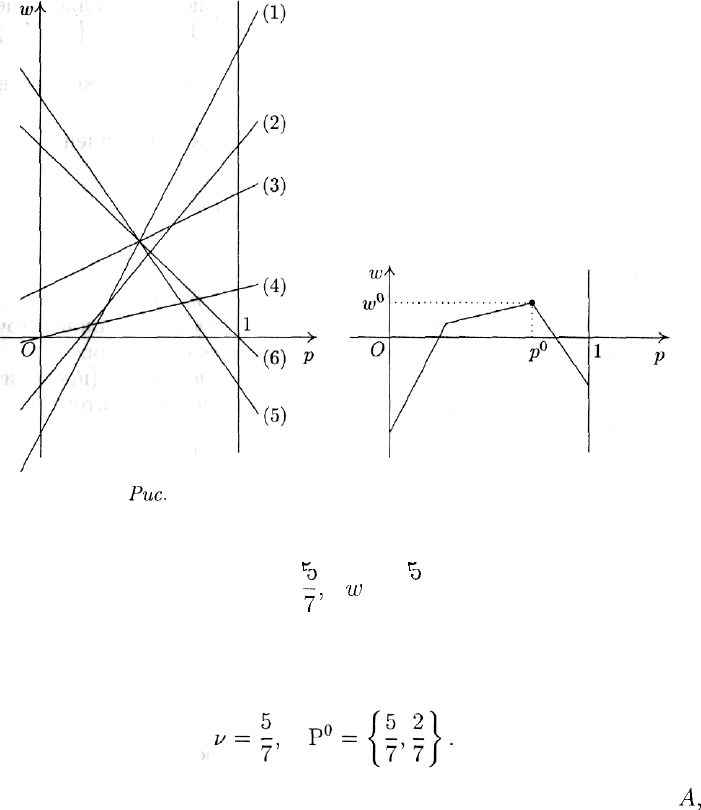
(рис. 1). Затем для каждого значения р, О ^ р ^ 1, путем визуального

сравнения соответствующих ему значений w на каждой из построен-

ных прямых определяется и отмечается наименьшее из них (рис. 2).

В результате описанной поцедуры получается ломаная, которая и

является графиком функции (1) (жирная линия на рис. 3).

Рис.

Рис. 3

Рис. 4

Эта ломаная как бы огибает снизу все семейство построенных

прямых, и по этой причине ее принято называть нижней огибающей

этого семейства.

326

17.3.

МЕТОДЫ РЕШЕНИЯ

MAТРИЧНЫХ

ИГР

3-й шаг. Построение нижней огибающей.

Строим на координатной плоскости (р,

ги)

все шесть прямых, ура-

внения которых получены на 2-м шаге

(рис.

5, масштаб по осям раз-

ный), и находим их нижнюю огибающую.

4-й

шаг. Отыскание цены игры и оптимальной смешанной стра-

тегии игрока А.

При построении нижней огибающей нетрудно определить, на пе-

ресечении каких двух из шести прямых лежит ее наивысшая точка.

В данном случае это прямые (4) и (5), заданные уравнениями w = р

w = — р + 5(1 — р) соответственно. Решая систему уравнений

w=p,

= —р + 5(1 — р),

327

Верхняя точка построенной нижней огибающей определяет и цену

игры —

и,

и оптимальную стратегию игрока А — Р°

{р°,

1 — р

}

(рис. 4).

Опробуем описанную схему решения 2 х n-игры на конкретном

примере.

Пример

Рассмотрим игру, заданную 2 х 6-матрицей

Решение.

1-й шаг. Анализ игры на наличие седловой точки.

Нижняя цена игры равна —1, верхняя — равна 1. Седловой точки

нет. Решение игры нужно искать в смешанных стратегиях.

2-й шаг. Вычисление средних выигрышей игрока А (проводится

при условии, что игрок В выбирает только чистые стратегии).

Из таблицы

легко получаем

ГЛАВА 11. МАТРИЧНЫЕ ИГРЫ

Рис.

Рис. 6

получаем

V = -

= -

(рис. б).

Тем самым, цена игры v и оптимальная стратегия Р° игрока А

соответственно равны:

Собственно, этим и заканчивается решение игры для игрока

Л,

поскольку его в первую очередь интересует отыскание собственной

оптимальной стратегии и ожидаемого наилучшего гарантированного

результата.

Замечание. Решающий матричную игру обычно отождествляет себя

с одним из игроков (как правило, это игрок А), считая другого своим

противником. Это связано еще и с тем, что в некоторых случаях

основное внимание уделяется поиску оптимальных стратегий только

игрока А, а стратегии противника могут вообще не интересовать ис-

следователя.

328

17.3. МЕТОДЫ РЕШЕНИЯ МАТРИЧНЫХ ИГР

Однако в целом ряде случаев оказывается важным знать опти-

мальные смешанные стратегии обоих игроков.

Как находится оптимальная смешанная стратегия игрока А, мы

уже описали. Покажем теперь, как отыскать оптимальную смешан-

ную стратегию игрока В.

Здесь в зависимости от формы нижней огибающей может пред-

ставиться несколько случаев.

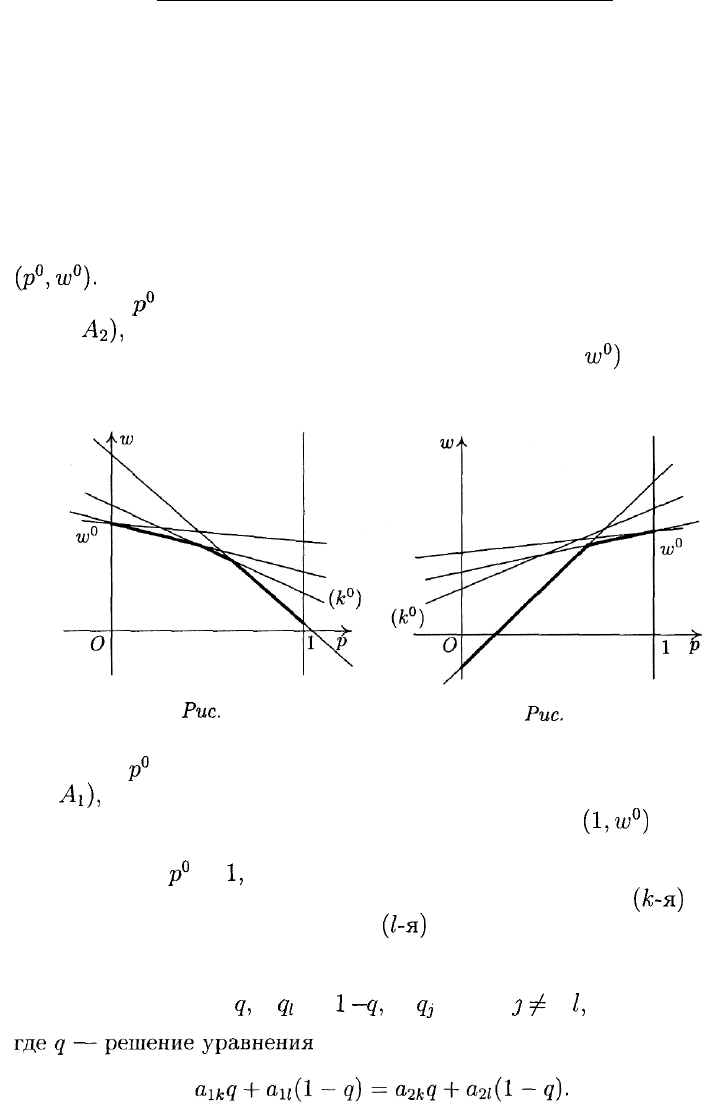
А. Нижняя огибающая имеет ровно одну наивысшую точку

(p°,w°).

1) Если

р°

= О (оптимальная стратегия игрока А — чистая стра-

тегия

Лг),

то игроку В выгодно применить чистую стратегию, со-

ответствующую прямой, проходящей через точку (0,

w°)

и имеющей

наибольший отрицательный наклон (рис. 7).

Рис.

2) Если

р°

= 1 (оптимальная стратегия игрока А — чистая страте-

гия

А\),

то оптимальной для игрока В является чистая стратегия,

соответствующая прямой, проходящей через точку

(1,го°)

и имею-

щей наименьший положительный наклон (рис. 8).

3) Если 0 <

р°

то в наивысшей точке нижней огибающей пере-

секаются по меньшей мере две прямые, одна из которых

(к-я)

имеет

положительный наклон, а другая

(1-я)

— отрицательный (рис. 9), и

оптимальная смешанная стратегия игрока В получается, если поло-

жить

Як =

Я.1

Я,

Чз

= 0,

к,

22 Зак. 7492

329

ГЛАВА 17. МАТРИЧНЫЕ ИГРЫ

Рис. 9

Рис. 10

Б. Нижняя огибающая содержит горизонтальный участок, соот-

ветствующий чистой стратегии

игрока

В,

которая и является оп-

тимальной для него (рис. 10).

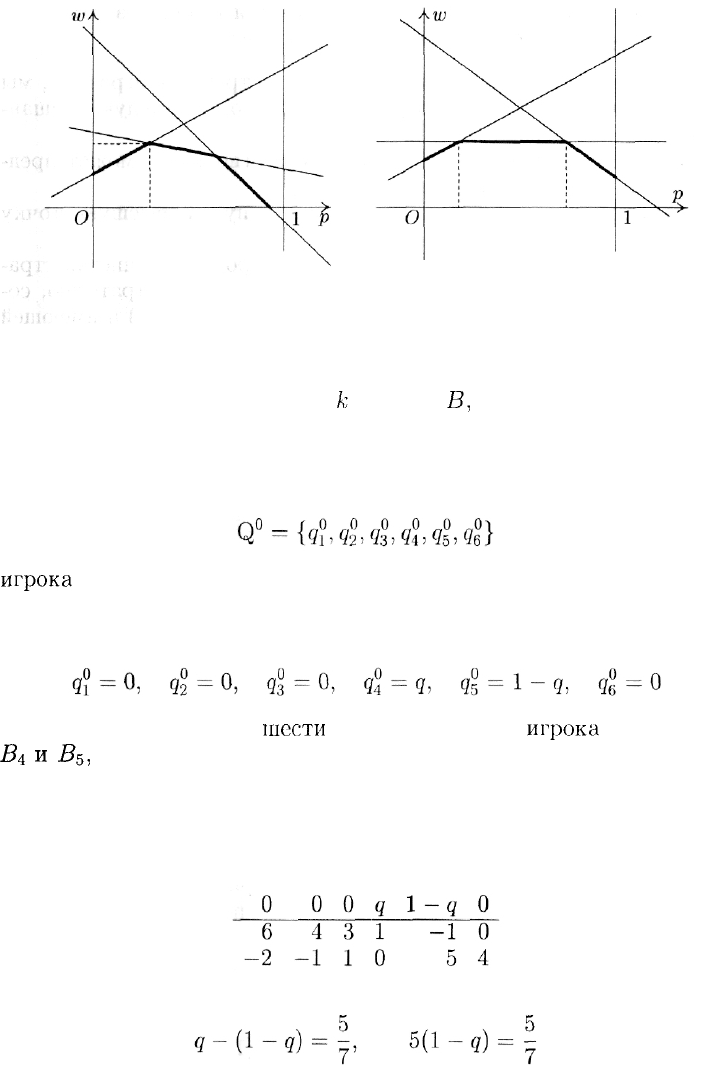
Покажем теперь, как найти полное решение игры из примера 4,

т. е. еще и оптимальную смешанную стратегию

игрока

В.

Для этого поступают так:

1) полагают

(выделяя тем самым из

шести

чистых стратегий

игрока

В стратегии

В$,

которые соответствуют прямым (4) и (5), определяющим

наивысшую точку нижней огибающей);

2) приравнивают любой из двух средних выигрышей игрока В

(игрок А выбирает только чистые стратегии), отвечающий предло-

женной смешанной стратегии

к цене игры:

330