Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

ИГРОВЫЕ МЕТОДЫ

рает свою стратегию, в результате чего складывается набор стра-

тегий, называемый ситуацией. Заинтересованность игроков в ситу-

ации проявляется в том, что каждому игроку в каждой ситуации

приписывается число, выражающее степень удовлетворения его ин-

тересов в этой ситуации и называемое его выигрышем в ней.

В этих условиях протекание конфликта состоит в выборе каждым

игроком своей стратегии и получении им в сложившейся ситуации

выигрыша из некоторого источника.

На этом пути создается теория игр с выигрышами.

Однако оценка игроком ситуации путем предположения о своем

выигрыше, вообще говоря, не всегда возможна практически и даже

не всегда имеет смысл. В подобных случаях иногда удается вместо

прямых численных оценок ситуаций указывать на их сравнительную

предпочтительность для отдельных игроков.

На этом пути создается теория игр с предпочтениями, включа-

ющая в себя и теорию игр с выигрышами.

В дальнейшем мы ограничимся рассмотрением только игр с выи-

грышами.

Изучение игр можно проводить с различных точек зрения.

Мы будем стремиться

к выработке принципов оптимальности, т. е. того критерия, по

которому поведение игроков следует считать оптимальным (разум-

ным, целесообразным);

к выяснению реализуемости этих принципов, т. е. установлению

существования оптимальных в выработанном смысле ситуаций, и

отысканию этих реализаций.

Одной из плодотворных форм реализации представлений об оп-

тимальности можно считать понятие равновесия, при котором скла-

дывается такая (равновесная) ситуация, в нарушении которой не

заинтересован ни один из игроков.

Именно ситуации равновесия могут быть предметом устойчивых

договоров между игроками (ни у одного из игроков не будет мотивов

к нарушению договора).

Кроме того, ситуации равновесия являются выгодными для ка-

ждого игрока: в равновесной ситуации каждый игрок получает наи-

больший выигрыш (разумеется, в той мере, в какой это от него за-

висит).

Если в игре ситуации равновесия (в пределах отпущенных воз-

можностей) нет, то, оставаясь в условиях стратегий, имеющихся у

игроков, мы сталкиваемся с неразрешимой задачей.

311

ИГРОВЫЕ МЕТОДЫ

При возникновении подобных случаев естественно ставить вопрос

о таком расширении первоначального понятия стратегии, чтобы сре-

ди ситуаций, составленных из

новых,

обобщенных стратегий, заве-

домо нашлись равновесные.

Если такие обобщенные стратегии существуют, то обычно они

представляются некоторыми комбинациями исходных стратегий.

Для того чтобы отличать прежние стратегии от новых, первые

называют

чистыми,

а вторые — смешанными стратегиями.

Весьма

плодотворным является представление смешанной стра-

тегии как случайного выбора игроками их чистых стратегий, при

котором случайные выборы различных игроков независимы в сово-

купности, а выигрыш каждого из них определяется как математиче-

ское ожидание случайного выигрыша.

Таким образом, преобразованная игра обычно называется сме-

шанным расширением исходной игры.

Проиллюстрируем сказанное на примере одного из самых про-

стых, но одновременно и наиболее изученных и продвинутых классов

игр, на так называемых матричных играх. Исследование матричных

игр интересно еще и потому, что к ним могут быть приближенно све-

дены многие игры более общего вида.

Затем мы рассмотрим позиционные и биматричные игры, а также

пример игры со многими участниками.

Глава 17

МАТРИЧНЫЕ ИГРЫ

Рассмотрим игру, в которой участвуют два игрока, причем каждый

из них имеет конечное число стратегий.

Обозначим для удобства одного из игроков через

А,

в другого —

через В.

Предположим, что игрок А имеет т стратегий:

А\,

...,

игрок В — п стратегий: В\,

. •.,

Пусть игрок А выбрал стратегию

Ai,

а игрок В — стратегию

Bk-

Будем считать, что выбор игроками стратегий

однознач-

но определяет исход игры — выигрыш

а^

игрока А и выигрыш

Ь^

игрока

В,

причем эти выигрыши связаны равенством

Последнее условие показывает, что в рассматриваемых обстоя-

тельствах выигрыш одного из игроков равен выигрышу другого, взя-

тому с противоположным знаком. Поэтому при анализе такой игры

можно рассматривать выигрыши только одного из игроков. Пусть

это будут, например, выигрыши игрока А.

Если нам известны значения

а^

выигрыша при каждой паре стра-

тегий (в каждой ситуации)

{Aj,

В^\,

i —

1,2,...,

то,

1,2,...,

п, то

их удобно записывать

или в виде прямоугольной таблицы, строки которой соответству-

ют стратегиям игрока А, а столбцы — стратегиям игрока В,

213ак.

7492

313

ГЛА

17.

МА ТРИЧНЫЕ ИГРЫ

или в виде матрицы

Полученная матрица имеет размер

гпхп

и называется матрицей

игры или платежной матрицей (отсюда и название игры — мат-

ричная) .

Рассматриваемую игру часто называют игрой т х п или т х п-

игрой.

Замечание. Матричные игры относятся к разряду так называемых

антагонистических игр, т. е. игр, в которых интересы игроков прямо

противоположны.

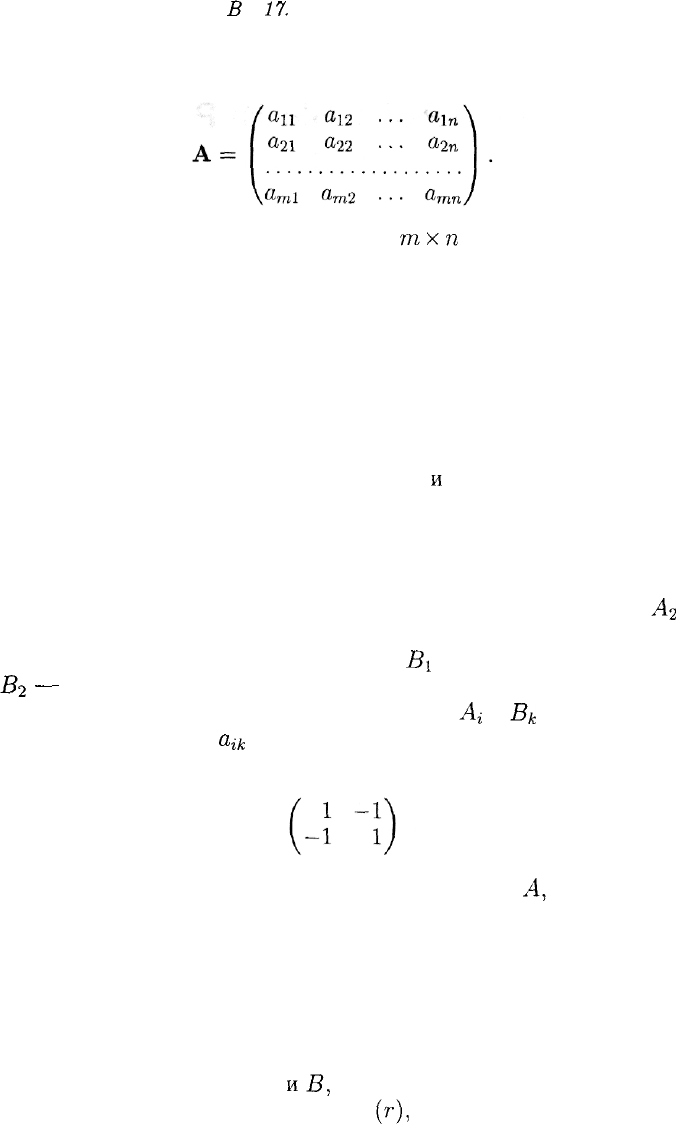
Пример 1. Каждый из двух игроков А

В одновременно и неза-

висимо друг от друга записывает на листе бумаги любое целое число.

Если выписанные числа имеют одинаковую четность, то игрок А

получает от игрока В 1 рубль, а если разную, то, наоборот, игрок А

платит 1 рубль игроку В.

У игрока А две стратегии: А\ — записать четное число и

А2

—

записать нечетное число.

У игрока В такие же две стратегии:

— записать четное число

— записать нечетное число.

Выбор игроками соответственно стратегий

В)-

однозначно оп-

ределяет исход игры:

— выигрыш игрока А.

Матрица этой 2 х 2-игры имеет следующий вид:

(здесь строки соответствуют стратегиям игрока

А,

а столбцы

стратегиям игрока В).

17.1. Равновесная ситуация

Рассмотрим следующий пример.

Пример 2. Два игрока А

В,

не глядя друг на друга, кладут на

стол по картонному кружку красного

(г),

зеленого (д) ИЛИ синего (6)

314

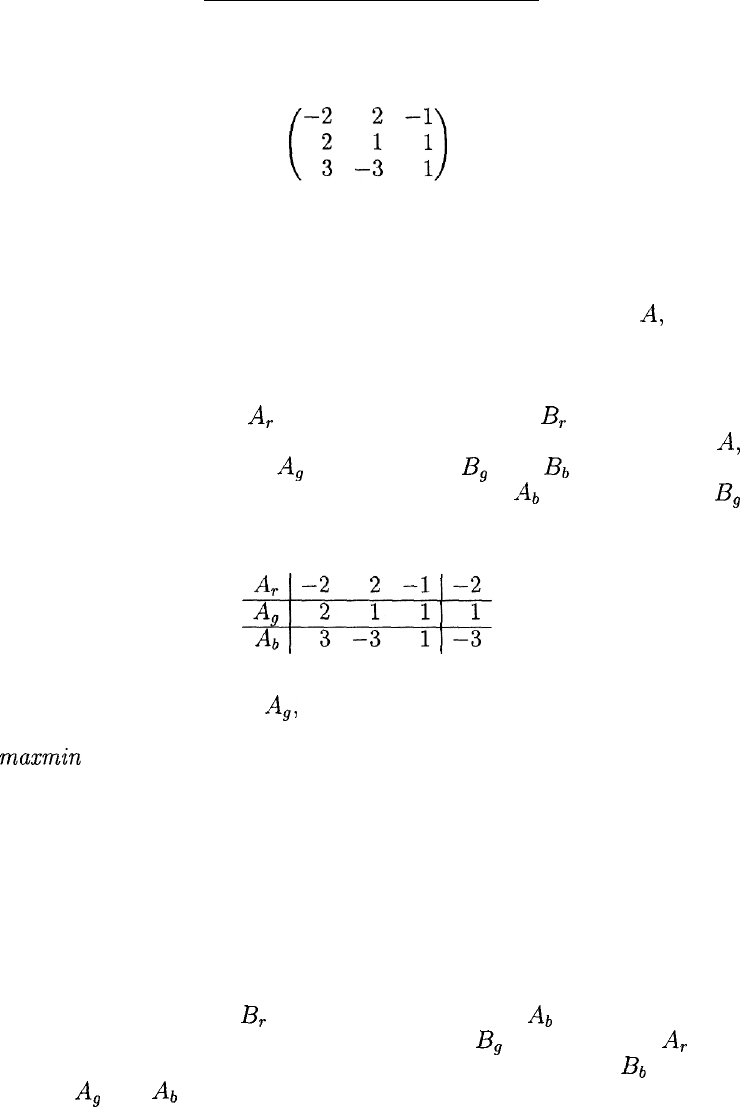
17.1. РАВНОВЕСНАЯ СИТУАЦИЯ

цвета, сравнивают цвета кружков и расплачиваются друг с другом

так, как показано в матрице игры:

(напомним, что у этой 3 х 3-матрицы строки соответствуют страте-

гиям игрока А, а столбцы — стратегиям игрока В).

Считая, что эта 3 х 3-игра повторяется многократно, попробуем

определить оптимальные стратегии каждого из игроков.

Начнем с последовательного анализа стратегий игрока

А,

не за-

бывая о том, что, выбирая стратегию игрока А, должно принимать

в расчет, что его противник В может ответить на нее той из своих

стратегий, при которой выигрыш игрока А будет минимальным.

Так, на стратегию

он ответит стратегией

(минимальный

выигрыш равен —2, что на самом деле означает проигрыш игрока

А,

равный 2), на стратегию

— стратегией

или

(минимальный

выигрыш игрока А равен 1), а на стратегию

Аь

— стратегией

(минимальный выигрыш игрока А равен —3).

Запишем эти минимальные выигрыши в правом столбце таблицы:

Максимин (rnaxmin). Неудивительно, что игрок А останавливает

свой выбор на стратегии

при которой его минимальный выигрыш

максимален (из трех чисел —2, 1 и —3 максимальным является 1),

maxmin = 1.

Если игрок А будет придерживаться этой стратегии, то ему гаран-

тирован выигрыш, не меньший 1, при любом поведении противника.

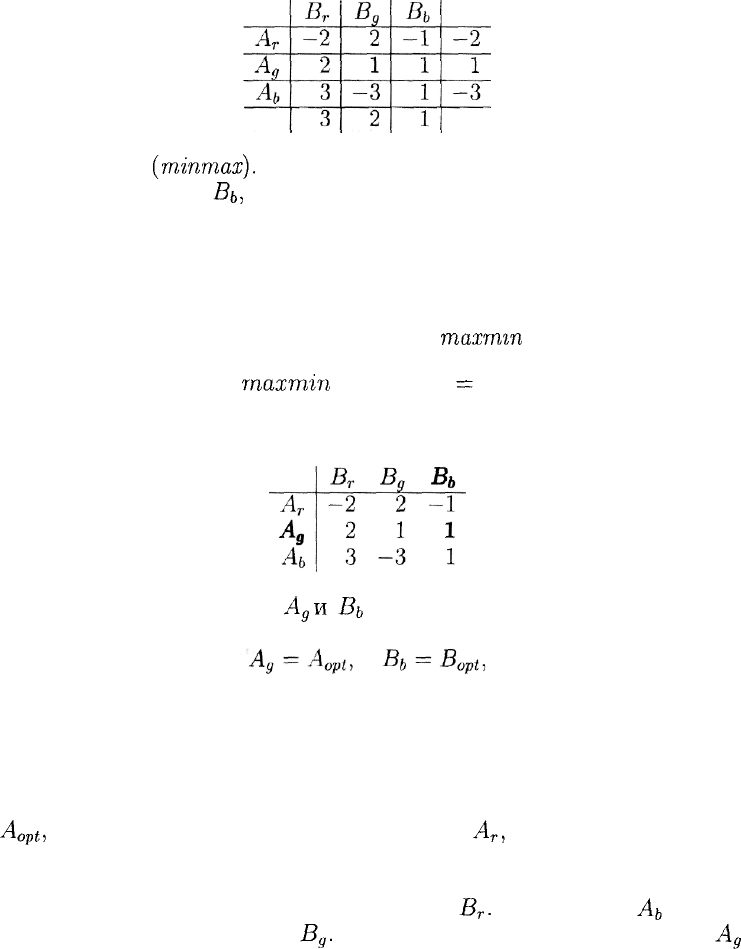
Аналогичные рассуждения можно провести и за игрока В. Так

как игрок В заинтересован в том, чтобы обратить выигрыш игрока А

в минимум, то ему нужно проанализировать каждую свою стратегию

с точки зрения максимального выигрыша игрока А.

Выбирая свою стратегию, игрок В должен учитывать, что при

этом стратегией его противника А может оказаться та, при которой

выигрыш игрока А будет максимальным.

Так, на стратегию

он ответит стратегией

Аь

(максимальный

выигрыш игрока А равен 3), на стратегию

— стратегией

(ма-

ксимальный выигрыш игрока А равен 2), а на стратегию

Вь

— стра-

тегией

или

Аь

(максимальный выигрыш игрока А равен 1).

315

ГЛАВА 11. МАТРИЧНЫЕ ИГРЫ

Эти максимальные выигрыши записаны в нижней строке таблицы

Минимакс

(minmax).

Неудивительно, если игрок В остановит свой

выбор на стратегии

Вь,

при которой максимальный выигрыш игрока

А минимален (из трех чисел 3, 2 и 1 минимальным является 1),

minmax = 1.

Если игрок В будет придерживаться этой стратегии, то при лю-

бом поведении противника он проиграет не больше 1.

Итак, в рассматриваемой игре числа

тахтгп

и minmax совпали:

rnaxmin

= minmax

(соответствующие элементы в таблице выделены жирным шриф-

том):

Выделенные стратегии

Вь

являются оптимальными для иг-

роков А и В,

в следующем смысле:

при многократном повторении игры отказ от выбранной стратегии

любого из игроков уменьшает его шансы на выигрыш (увеличивает

шансы на проигрыш).

В самом деле, если игрок А не будет придерживаться стратегии

Agpt,

а выберет иную стратегию, например

то вряд ли стоит рас-

считывать на то, что игрок В этого не заметит. Конечно, заметит и

не преминет воспользоваться своим наблюдением. Ясно, что в этом

случае он отдаст предпочтение стратегии

Д..

А на выбор

Аь

игрок

В ответит, например, так:

В результате отказа от стратегии

выигрыш игрока А уменьшится.

Если же от оптимальной стратегии отказывается игрок В, вы-

бирая, например, стратегию Д., то игрок А может ответить на это

316

17.1. РАВНОВЕСНАЯ СИТУАЦИЯ

стратегией

Аь

и тем самым увеличить свой выигрыш. В случае стра-

тегии

ответ игрока А —

Тем самым ситуация

{А

,Вь}

оказывается равновесной.

Еще раз подчеркнем, что элементами матрицы игры являются

числа, описывающие выигрыш игрока А. Более точно, выигрыш со-

ответствует положительному элементу платежной матрицы, а отри-

цательный указывает на проигрыш игрока А.

Матрица выплат игроку В получается из матрицы игры заменой

каждого ее элемента на противоположный.

Рассмотрим теперь произвольную матричную игру:

(строки заданной т х n-матрицы соответствуют стратегиям игрока

А, а столбцы — стратегиям игрока В) и опишем общий алгоритм, по-

средством которого можно определить, есть ли в этой игре ситуация

равновесия или ее нет.

В теории игр предполагается, что оба игрока действуют разумно,

т. е. стремятся к получению максимального выигрыша, считая, что

соперник действует наилучшим (для себя) образом.

А. Действия игрока А.

1-й шаг. В каждой строке матрицы А находится минимальный

элемент

Полученные числа

приписываются к заданной таблице в виде правого добавочного

столбца:

оц

Пояснение. Выбирая стратегию

А{,

игрок А должен рассчитывать

на то, что в результате разумных действий противника (игрока В)

он выиграет не меньше чем

с^.

317

ГЛАВА 17. МАТРИЧНЫЕ ИГРЫ

Специально отметим, что выбранное число

является одним из

элементов заданной матрицы А.

Пояснение. Действуя наиболее осторожно и рассчитывая на наи-

более разумное поведение противника, игрок А должен остановиться

на той стратегии

АГ,

ДЛЯ которой число

а.{

является максимальным.

Если игрок А будет придерживаться стратегии, выбранной опи-

санным выше способом, то при любом поведении игрока В игроку А

гарантирован выигрыш, не меньший

а.

Число

называется нижней ценой игры.

Принцип построения стратегии игрока А, основанный на макси-

мизации минимальных выигрышей, называется принципом макси-

мина, а выбираемая в соответствии с этим принципом стратегия

AJO

максиминной стратегией игрока А.

В. Действия игрока В.

1-й шаг. В каждом столбце матрицы А ищется максимальный

элемент

Полученные числа

приписываются к заданной таблице в виде нижней добавочной стро-

ки:

Пояснение. Выбирая стратегию

к,

игрок В должен рассчитывать

на то, что в результате разумных действий противника (игрока А)

он проиграет не больше, чем

/З/.-

318

17.1. РАВНОВЕСНАЯ СИТУАЦИЯ

2-й шаг. Среди чисел

выбирается минимальное число

/3 =

min0

или подробнее:

(3 =

min

max

a^.

Выбранное число (3 также является одним из элементов заданной

матрицы А.

Пояснение. Действуя наиболее осторожно и рассчитывая на наи-

более разумное поведение противника, игрок В должен остановиться

на той стратегии

В^,

для которой число

(3^

является минимальным.

Если игрок В будет придерживаться стратегии, выбранной опи-

санным выше способом, то при любом поведении игрока А игроку В

гарантирован проигрыш, не больший (3.

Число (3 называется верхней ценой игры.

Принцип построения стратегии игрока В, основанный на мини-

мизации максимальных потерь, называется принципом

минимакса,

а выбираемая в соответствии с этим принципом

стратегия-

В^р

—

минимаксной стратегией игрока В.

Нижняя цена игры

и верхняя цена игры

всегда связаны не-

равенством

Замечание. Реализация описанного алгоритма требует 2тп — 1 срав-

нений элементов матрицы А:

(п —

1)га

+ т — 1 = ran — 1

сравнений для определения

а,

(т — 1)п + п — 1 = тп — 1

сравнений для определения (3 и одно сравнение полученных чисел

(3.

Если

319

ГЛАВА 17. МАТРИЧНЫЕ ИГРЫ

или подробнее:

то ситуация

{AiO,Bko}

оказывается равновесной и ни один из игро-

ков не заинтересован в том, чтобы се нарушить (в этом нетрудно

убедиться путем рассуждений, подобных проведенным при анализе

игры в примере 2).

В том случае, когда нижняя цена игры равна верхней цене игры,

их общее значение называется просто ценой игры и обозначается

через v.

Цена игры совпадает с элементом

матрицы игры А, располо-

женным на пересечении г -й строки (стратегия

А,о

игрока А) и

к°-го

столбца (стратегия

игрока

В),

— минимальным в своей строке

и максимальным в своем

столбце.

Этот элемент называют седловой точкой матрицы А или точкой

равновесия, а про игру говорят, что она имеет седловую точку.

Стратегии

Л^о

о,

соответствующие седловой точке, называ-

ются оптимальными, а совокупность оптимальных ситуаций и цена

игры — решением, матричной игры с седловой точкой.

Замечание. Седловых точек в матричной игре может быть несколь-

ко, но все они имеют одно и то же значение.

Матричные игры с седловой точкой важны и интересны, однако

более типичным является случай, когда применение описанного ал-

горитма приводит к неравенству

а<0.

Как показывает следующий пример, в этом случае предложен-

ный выбор стратегий уже, вообще говоря, к равновесной ситуации

не приводит и при многократном се повторении у игроков вполне

могут возникнуть мотивы к нарушению рекомендаций, основанных

на описанной последовательности действий игроков А и В.

Пример 3. Рассмотрим 3 х 3-игру, заданную матрицей

320