Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

Ц.1

ОЦЕНКИ ВЕРОЯТНОСТИ СОБЫТИЯ

Теперь осталось воспользоваться формулами (2) и (3), подставив

туда данные в условии

а,

п и найденные X,

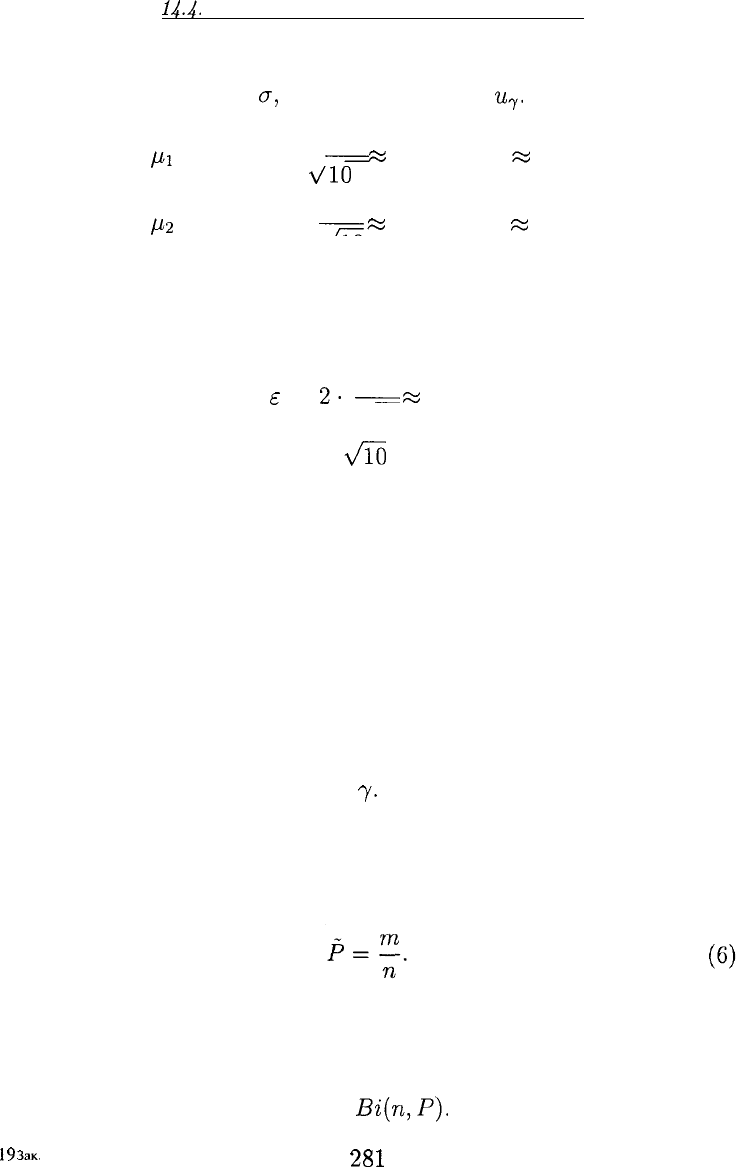
Имеем:

/ii

= 10,8 - 2

•

—=

яз

10,8 - 3,16

7,64,

vlO

= 10,8 + 2 •

-7=

яз

10,8 + 3,16

13,96.

V10

Таким образом, искомым доверительным интервалом является ин-

тервал (7,64; 13,96).

Для погрешности е получаем следующее значение:

—=

3,16.

vTo

14.4. Оценки вероятности события

Пусть некоторое событие происходит в результате единичного испы-

тания с вероятностью Р, которая нам неизвестна. Однако ситуация

позволяет многократно повторить испытание и подсчитать, сколько

раз произошло указанное событие. Более точно: пусть произведено п

испытаний, в которых событие произошло т раз. Здесь в отличие от

предыдущих рассмотрений исходными данными для анализа будут

всего два числа — п и т.

Задача, которую мы будем рассматривать, заключается в отыс-

кании оценки неизвестной вероятности Р по имеющимся данным п,

т и доверительной вероятности

у.

Точечная оценка

Не вызывает сомнений, что точечная оценка Р вероятности Р опре-

деляется следующим соотношением:

Докажем несмещенность и состоятельность этой оценки.

При любом фиксированном п величина т является случайной

величиной с биномиальным законом распределения:

т =

Вг(п,Р).

3ак.

7492

281

282

Пользуясь этим обстоятельством, можно найти границы довери-

тельного интервала

(Pi,

P2)

методом, сходным с методом вычисле-

ния доверительного интервала для математического ожидания нор-

мального распределения. Выпишем сразу результат:

Ц.5.

ЗАДАНИЯ И ОТВЕТЫ

где

— решение уравнения

Ф(щ)

(9)

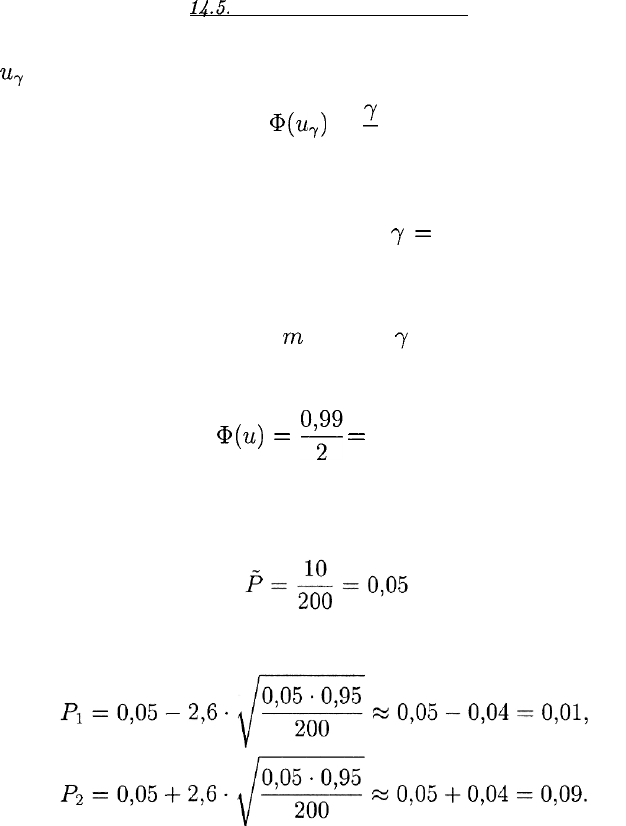
Пример 3. Из 200 случайным образом отобранных изделий не-

которой фирмы 10 оказались бракованными. Найти доверительный

интервал, содержащий с надежностью

0,99 долю бракованных

изделий среди всей продукции фирмы.

Решение. Здесь

п = 200,

= 10,

= 0,99.

Применяя формулы (9), (6), (7), (8), получаем, что

ф(„)

°|?

0,495,

и = 2,6

(напомним, что это значение находится по таблице),

(это точечная оценка),

Таким образом, доверительный интервал оказался следующим:

(0,01; 0,09). Иными словами, с доверительной вероятностью 0,99 до-

ля бракованных изделий лежит в промежутке между 1% и 9%.

14.5. Задания и ответы

1. Выборка из большой партии электроламп содержит 100 ламп.

Средняя продолжительность работы лампы из выборки оказалась

равной 1000 ч. Найти 95%-й доверительный интервал для средней

283

ГЛАВА

Ц.

ТОЧЕЧНЫЕ И

ИНТЕРБАЛЬНЫЕ

ОЦЕНКИ

продолжительности работы лампы, случайно выбранной из всей

партии, если время работы является нормально распределенной слу-

чайной величиной со стандартным отклонением 40 ч.

Ответ: (992, 1008).

2. У нормально распределенной случайной величины стандарт-

ное отклонение равно 2. Найти минимальный объем выборки, при

котором с надежностью, не меньшей 0,8, погрешность оценки мате-

матического ожидания будет меньше 0,3.

Ответ: 76.

3. Из 400 случайным образом отобранных изделий некоторой

фирмы 20 оказались бракованными. Найти доверительный интер-

вал, содержащий с надежностью

0>99

долю бракованных изде-

лий среди всей продукции фирмы.

Сравните полученный результат с тем, который был получен при

разборе примера 3.

Ответ: (0,02; 0,08).

Глава 15

КОРРЕЛЯЦИЯ И РЕГРЕССИЯ

Одним из важных приложений методов математической статисти-

ки является установление зависимости между двумя или более на-

блюдаемыми величинами. При этом наряду с раздельным анализом

выборок, составленных из значений этих величин, возможен и сов-

местный анализ. Ниже рассматриваются некоторые методы такого

анализа.

15.1. Корреляция

Рассмотрим ситуацию, когда в результате эксперимента измеряется

не одна, а сразу две случайные величины, скажем X и

Примера-

ми здесь могут служить врачебный осмотр, где у каждого пациента

измеряют рост и вес; измерение средней температуры воздуха в двух

городах в течение определенного дня; проверка квалификации ра-

бочих, когда фиксируются производительность и стаж работы.

Итак, исходными данными являются пары чисел (точки)

(Xl,Vl),

(

2,У2),

•••А

п,Уп),

(1)

где п — число испытаний. Наряду с анализом величин X и Y по

отдельности представляет интерес исследование возможной зависи-

мости между ними. Являются ли величины X и Y независимыми?

Если же между ними имеется некоторая зависимость, то какова она?

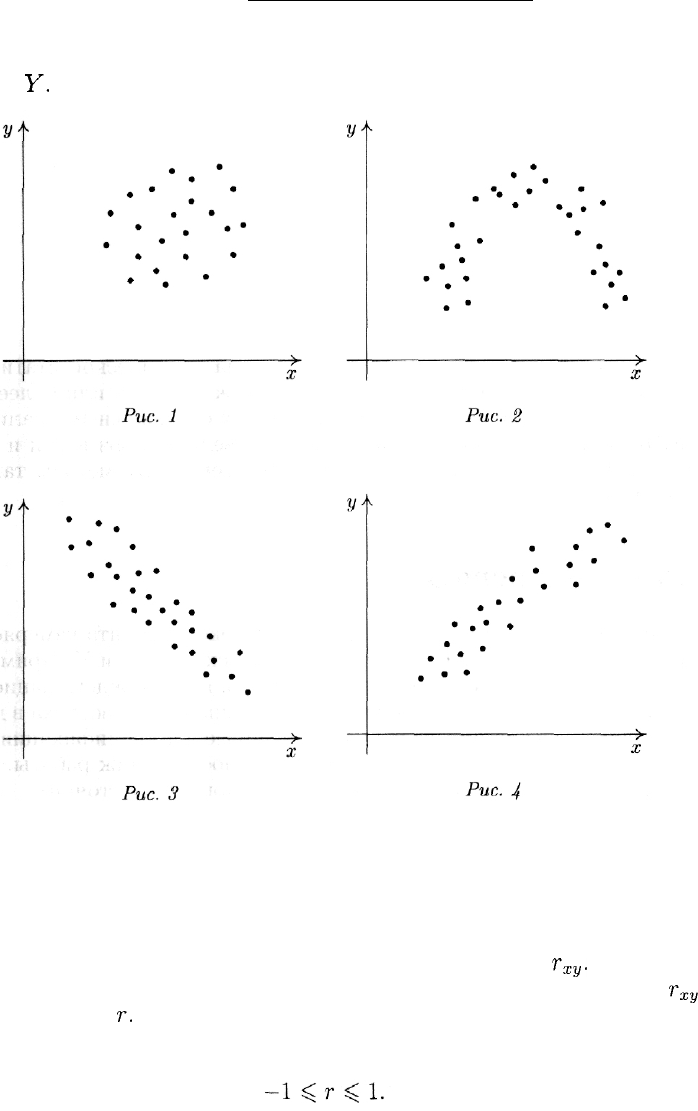
Обратимся к рис. 1-4. На них изображены различные виды графи-

ков (или диаграмм) рассеяния, т. е. нанесены точки (1). Величины X

и Y на рис. 1, по-видимому, независимы: зная, какое значение при-

няла величина X, ничего нельзя сказать о значении Y. На рис. 2-4

зависимость налицо: зная значение, которое приняла величина X в

285

ГЛАВА 15. КОРРЕЛЯЦИЯ И РЕГРЕССИЯ

результате испытания, можно довольно точно сказать, каково зна-

чение

Зависимость на рис. 3 и 4 близка к линейной, т. е. точки заметным

образом группируются вокруг некоторой прямой. В таких случаях

говорят, что величины X и Y коррелированы. Существует простой

способ определения степени коррелированности случайных величин.

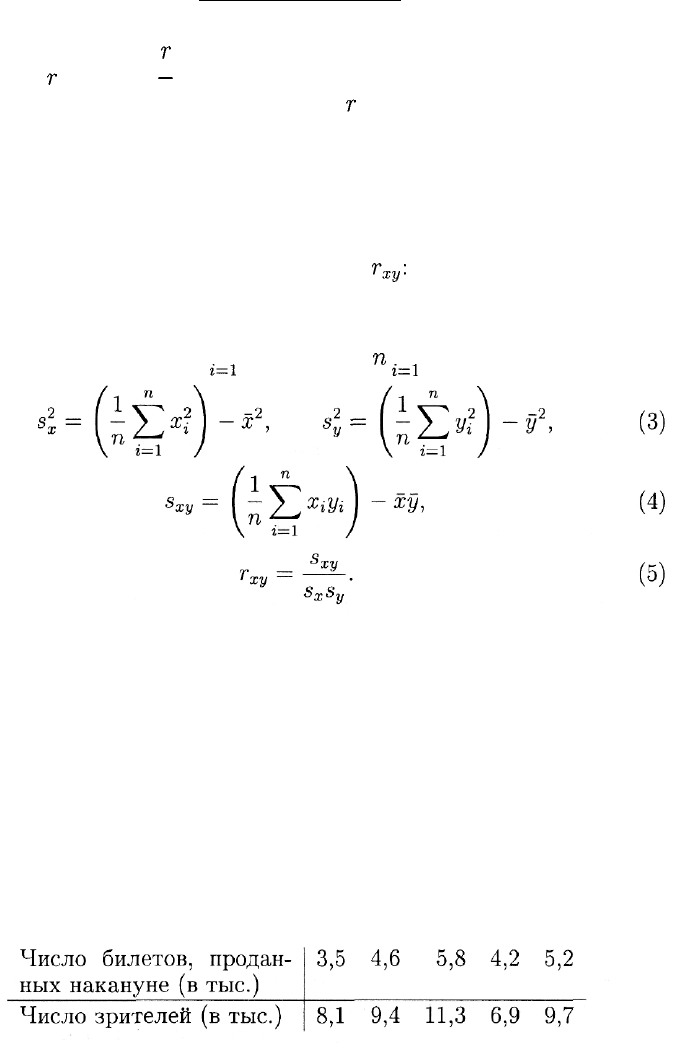
Он основан на вычислении коэффициента корреляции

ху

Если по-

нятно, о каких случайных величинах идет речь, будем вместо

ху

писать просто

г.

Коэффициент корреляции обладает следующим свойством:

286

15.1. КОРРЕЛЯЦИЯ

При этом чем ближе

к нулю, тем слабее корреляция. И наоборот,

чем ближе

к 1 или — 1, тем сильнее корреляция, т. е. зависимость

между X и Y близка к линейной. Если

в точности равно 1 или —1,

то точки (1) лежат на одной прямой.

Подчеркнем, что коэффициент корреляции отражает степень ли-

нейной зависимости между величинами. При наличии ярко выра-

женной зависимости другого вида (например, квадратичной) он мо-

жет быть близок к нулю.

Приведем формулы для вычисления

ху

п п

i=\

г=1

Пример. Рассмотрим проблему, которая стоит перед администра-

цией некоторого крытого стадиона, где проходят матчи, концерты и

другие развлекательные мероприятия. Перед каждым таким меро-

приятием требуется оценить, какое количество зрителей придет, это

необходимо для оптимальной организации работы различных вспо-

могательных служб. Один из подходов к решению этой проблемы —

учет предыдущего опыта. В частности, можно предположить, что

окончательное число зрителей сильно зависит от того, сколько биле-

тов продано за день до мероприятия (как раз за сутки определяется

план работы вспомогательных служб).

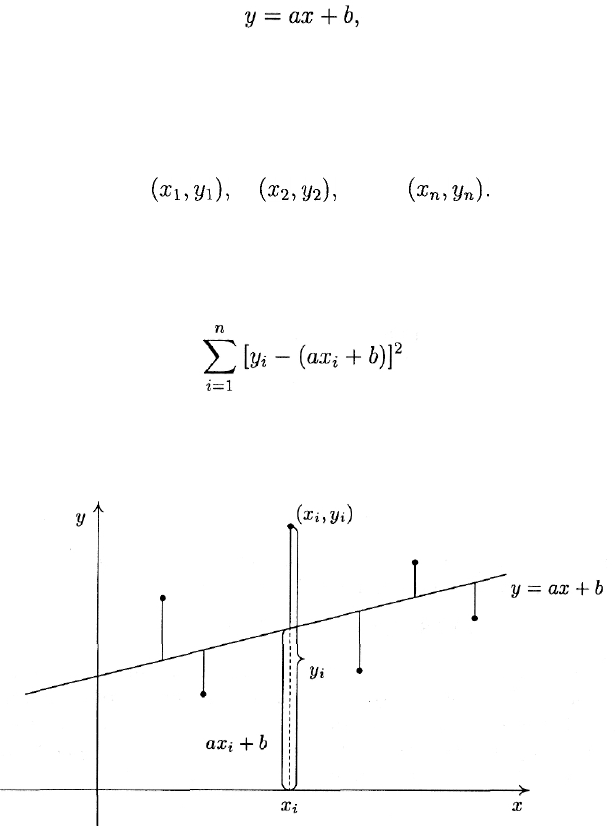
Пусть опыт первых пяти мероприятий этого года таков:

Каков коэффициент корреляции между числом проданных накануне

билетов и числом зрителей?

287

ГЛАВА 15. КОРРЕЛЯЦИЯ И РЕГРЕССИЯ

Таким образом, коэффициент корреляции

оказался довольно

близким к единице. Этим обстоятельством можно воспользоваться

для прогнозирования числа зрителей по имеющейся накануне ин-

формации. О том, каким образом это делается, см. в продолжении

этого примера на с. 290.

288

Эти суммы подставим затем в формулы (2)-(5). Имеем:

Решение. Примем число билетов за X, а число зрителей за Y. В

таблице даны пять реализаций пары случайных величин — пары

чисел

(xi,yi),

г — 1,...,5. Для расчета коэффициента корреляции

удобно найти

сначала

суммы

15.2. РЕГРЕССИЯ

15.2. Регрессия

Предположим, что зависимость между случайными величинами X

и Y близка к линейной (в этом случае коффициент корреляции г

близок к 1 или —1). Тогда естественно ставить вопрос об отыскании

функции

(6)

которая наилучшим образом выражает зависимость Y от X. Для

нахождения такой функции пользуются методом наименьших ква-

дратов.

Итак, пусть даны п пар чисел (иначе говоря, п точек):

(Zl,yi),

(Х

,У2),

•••,

(х

,Уп)-

Требуется найти такую прямую, чтобы сумма квадратов "отклоне-

ний" этих точек от прямой (6) была как можно меньше. Это означает,

что выражение

(7)

должно быть минимальным (на рис. 5 отклонения изображены в ви-

де вертикальных отрезков).

Рис. 5

289

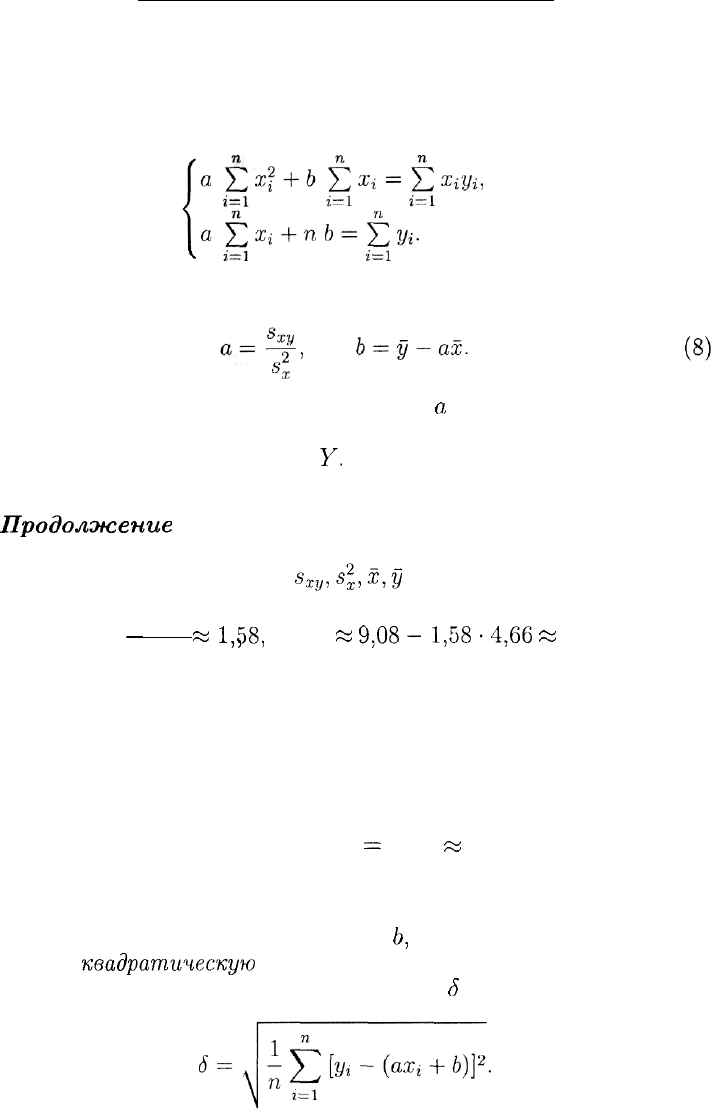
ГЛАВА 15. КОРРЕЛЯЦИЯ И РЕГРЕССИЯ

Выражение (7) является функцией двух переменных а и b

(поскольку результаты наблюдений заданы). Можно показать, что

выражение (7) принимает минимальное значение, если величины а

и b связаны соотношениями

Эта система имеет единственное решение:

Найдя значения неизвестных параметров

и 6, мы найдем тем са-

мым прямую (6), наилучшим образом выражающую статистическую

связь между величинами X и

Полученная прямая называется

прямой регрессии Y на X.

Продолоюение

примера (начало см. на с. 287). Для прогнози-

рования числа зрителей надо найти прямую регрессии Y на X. Под-

ставим найденные значения

,s^.,x,y

в формулы (8). Получаем

О 9972

а =

«1,58, b

9,08-

1,58

-4,66

яз

1,72.

0,6304

' '

Таким образом, прямая регрессии имеет уравнение

у = 1,58 • х + 1,72.

Если, например, за день до мероприятия продано 4300 билетов,

то предполагаемое число зрителей составляет

у = 1,58 • 4,3 + 1,72

8,514

8,5 тыс.

Если прямая регрессии найдена, можно оценить, насколько хо-

рошо она приближает результаты наблюдений. Подставляя в вы-

ражение (7) найденные значения а и

Ь,

вычислим так называемую

среднюю

квадратическую

погрешность или ошибку уравнения ре-

грессии, которую будем обозначать буквой

(дельта):

290