Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

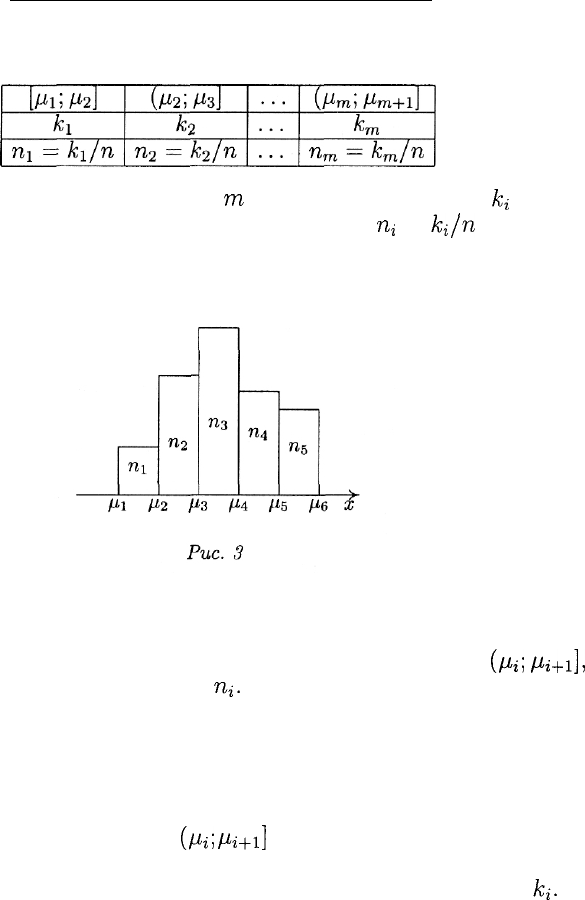
13.2. ПЕРВИЧНАЯ ОБРАБОТКА ДАННЫХ

блицу частот:

Здесь п — число всех измерений,

— число интервалов,

/с,

— ко-

личество чисел, приходящихся на г-й интервал,

ki/n

— относи-

тельная частота попадания в г-й интервал. Интервалы обычно берут

одинаковой длины, хотя это и не обязательно.

Графической иллюстрацией интервальной таблицы частот явля-

ется гистограмма (рис. 3). Гистограмма представляет собой ступен-

чатую линию; основанием г-й ступеньки является интервал

(/^;

//i+i],

а площадь этой ступеньки равна

щ.

Замечание 2. Число интервалов т выбирают из соображений на-

глядности получающейся гистограммы. Обычно т лежит в пределах

от 5 до 15.

Замечание 3. Если интервалы

(^;

/Xj+i]

выбраны одинаковой длины,

то площади ступенек гистограммы пропорциональны их высотам, и

в этом случае можно отмечать на оси ординат просто частоты

к{.

Пример 2. Предположим, что студенты некоторой группы, со-

стоящей из 25 человек, написали контрольную работу. Каждый сту-

дент получил определенное количество баллов. Приведем эти баллы

(в порядке алфавитного списка группы):

75, 145, 150, 180, 125, 150, 150, 165, 95, 135, 130, 70, 130,

105, 135, 135, 100, 160, 60, 85, 120, 60, 145, 150, 135.

271

ГЛАВА 13. О МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ

Требуется построить интервальную таблицу частот и гистограмму.

Нетрудно найти среди приведенных чисел минимальное и макси-

мальное — это числа 60 и 180. Таким образом, все значения лежат на

отрезке [60;180]. Разобьем этот отрезок, например, на т — 6 равных

частей. После этого подсчитаем число значений, попавших в каждый

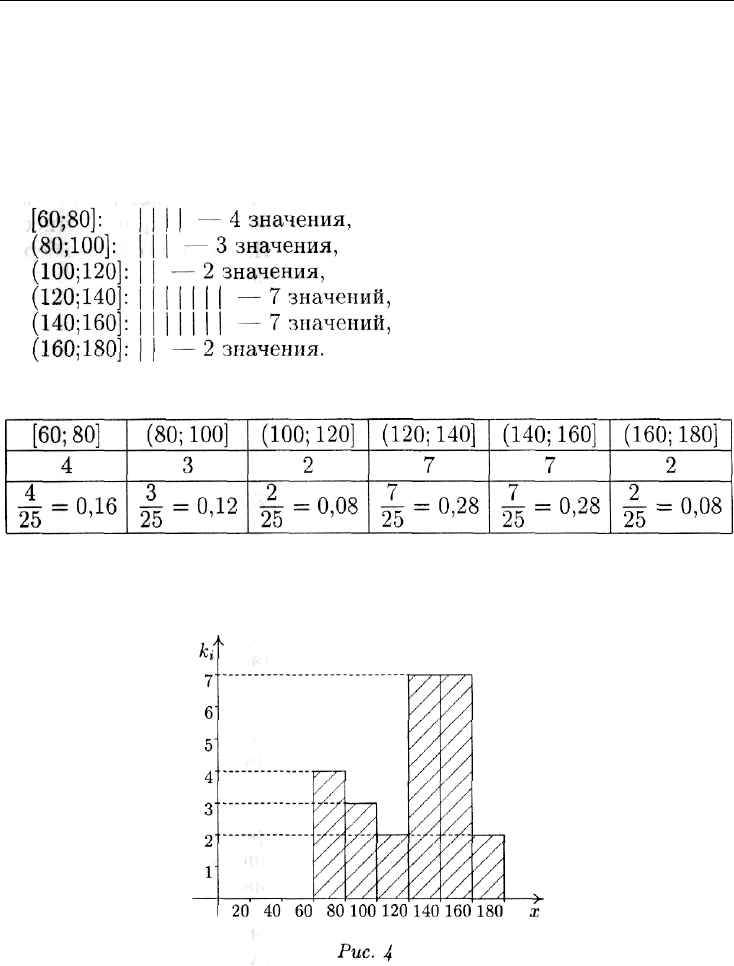
интервал (воспользуемся методом, описанным в примере 1):

Построим теперь интервальную таблицу частот:

Соответствующая гистограмма изображена на рис. 4. На вертикаль-

ной оси проставлены частоты — см. замечание 3.

Глава

ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ

ОЦЕНКИ

Выше были рассмотрены некоторые методы первичной обработки

данных, в ходе которой имеющиеся "сырые" результаты наблюде-

ний преобразуются для достижения большей наглядности. Теперь

мы рассмотрим методы, позволяющие, исходя из тех же данных, де-

лать предположения относительно числовых характеристик наблю-

даемой случайной величины — математического ожидания и диспе-

рсии.

14.1. Точечные оценки

При помощи таблицы частот либо гистограммы можно судить (хотя

бы примерно) о характере распределения наблюдаемой случайной

величины. Однако часто интерес представляют численные харак-

теристики распределения — математическое ожидание, дисперсия

и др. Это обусловлено тем, что в процессе принятия решения удоб-

нее опираться на небольшое число значимых параметров.

В связи с этим возникает задача: исходя из набора значений (вы-

борки)

Х\,

Х2,

. . . ,

величины X, полученного в результате п независимых наблюдений,

оценить значение математического ожидания

ЕХ,

дисперсии DX

либо еще какого-нибудь параметра. Пока наши рассуждения носят

общий характер, мы будем обозначать оцениваемый параметр бу-

квой в (тэта).

Повторим сказанное иными словами. Имеется случайная величи-

на X, значения (реализации) которой

х\,

х?,...,

каким-либо обра-

273

ГЛАВА

Ц.

ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ

зом становятся нам известными. (Этой случайной величиной может

быть число посетителей данного магазина в течение дня, рост в сан-

тиметрах студента данного вуза, годовой доход гражданина данной

страны и

пр.)

У величины X имеется, скажем, математическое ожи-

дание, которое нам неизвестно. Требуется найти способ, при помощи

которого по известным реализациям величины X можно разумным

образом оценить неизвестное математическое ожидание.

Сейчас мы рассмотрим, каким образом неизвестный параметр

оценивается одним числом. Такая оценка называется точечной.

Любая оценка для 9 - обозначим ее

•-- будет представлять

собой некоторое выражение, составленное из символов

х\,

,...,

в =

9(х

,...,х

Тем самым 9 будет случайной величиной (принимающей свои зна-

чения в результате п опытов над X). Ее закон распределения будет

зависеть от закона распределения случайной величины X (послед-

нему подчинена каждая из величин

х\,

,...,

)

и от числа наблю-

дений п.

Замечание. Подчеркнем, что на момент принятия решения о значе-

нии параметра в (т. е. после проведения испытаний (наблюдений))

величины

Xi,X'

,...

,х

являются конкретными числами. Однако на

момент, когда выбирается сам метод (алгоритм, формула) вычисле-

ния

величины

Х\,х

,...

,х

являются случайными, ведь еще неиз-

вестно, какие именно значения они примут.

Пример 1. Студент размышляет, ехать ли ему домой или ид-

ти в библиотеку. Не находя решающих аргументов в пользу того

или другого, он решает провести испытание — подбросить монету,

и если выпадет герб, то ехать домой (в противном случае — идти

в библиотеку). В сущности, решение тем самым принято (определен

алгоритм действий). Однако до подбрасывания монеты неизвестно,

что же выпадет, герб или цифра (соответственно неизвестно и на-

правление дальнейших передвижений студента).

Естественно предъявить к оценке 9 некоторые требования. Упо-

мянем два важнейших.

1) Желательно, чтобы при использовании величины

вместо не-

известного параметра в мы не делали систематических ошибок ни в

274

Ц.1.

ТОЧЕЧНЫЕ

ОЦЕНКИ

сторону завышения, ни в сторону занижения, т. е. чтобы выполня-

лось равенство

Ев

= 9.

Оценка, удовлетворяющая такому условию, называется несмещен-

ной.

2) Желательно, чтобы с увеличением числа п опытов значения

случайной величины

концентрировались около в все более тесно,

т. е. чтобы с ростом п точность оценки возрастала. Поскольку мерой

рассеяния случайной величины вокруг ее математического ожида-

ния является дисперсия, это требование можно сформулировать так:

—>

0 при п

—>

оо

(дисперсия оценки стремится к нулю при неограниченном возраста-

нии числа наблюдений). Оценка, удовлетворяющая такому условию,

называется состоятельной.

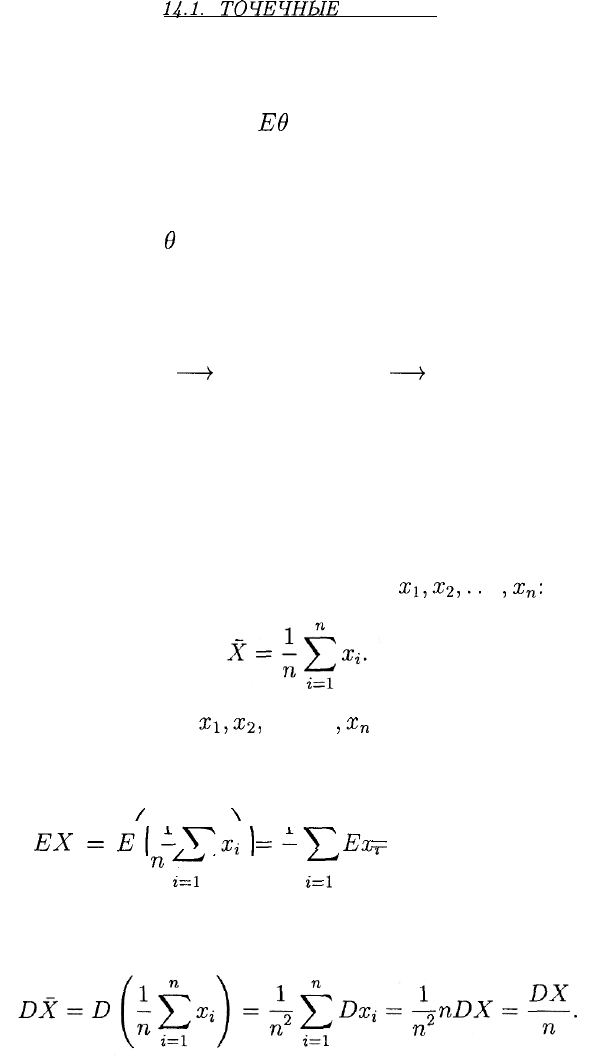
Рассмотрим важный пример — точечную оценку для математи-

ческого ожидания EX. Таким образом, в данном случае в = EX. В

качестве такой оценки примем так называемое эмпирическое сред-

нее, т. е. среднее арифметическое величин

х\,Х2,..

•

,х

;

Случайные величины

Х\,Х2,

• • •

,х

имеют один и тот же закон

распределения, совпадающий с законом распределения величины X.

Поэтому

/ п \ п

ЕХ

Е\-У^Хг\

=-У"Ех

-пЕХ = EX.

} п ^-^ п

г-1

г=1

Таким образом, оценка X является несмещенной. Дисперсия этой

оценки вычисляется следующим образом:

Выражение DX/n, очевидно, стремится к нулю при неограниченном

возрастании п. Отсюда вытекает состоятельность оценки X.

275

ГЛАВА

ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ

Соотношения

EX, DX =

-DX

(1)

понадобятся нам в дальнейших рассмотрениях.

14.2. Интервальные оценки

Рассмотренная в предыдущем пункте точечная оценка часто быва-

ет достаточной для практических выводов. Однако если есть необ-

ходимость в более детальном анализе, то надо оценить, насколько

истинное значение параметра расходится с точечной оценкой этого

значения.

В этом случае можно поступить следующим образом. Выберем

интервал

(#i,#2)

таким образом, чтобы вероятность включения в

этот интервал параметра в была достаточно велика (близка к едини-

це). Говоря более строго, это означает, что вероятность выполнения

двойного неравенства

9i(Xi,X2

..,Х

)<в<

(х

,Х

,...,Х

)

не меньше заданного числа у.

Вероятность у называется доверительной вероятностью или на-

дежностью, а интервал

(01,0г)

—

доверительным интервалом, (со-

ответствующим доверительной вероятности

7)-

Обычно значение у

выбирают равным 0,95 либо 0,99.

Рассмотренная оценка называется интервальной. Еще раз под-

черкнем, что интервальная оценка зависит не только от имеющихся

данных, но и от требуемой надежности

у.

Методы построения интервальных оценок будут обсуждаться в

последующих разделах. Сейчас же приведем неформальный пример,

поясняющий различие точечной и интервальной оценок.

Когда о каком-либо человеке говорят: "Ему примерно 38 лет", это

ни что иное, как точечная оценка возраста. Когда же говорят: "Ему

лет 35-40", это интервальная оценка, доверительный интервал —

(35;40). Надежность оценки при этом в явном виде не указывается,

но предполагается довольно близкой к единице.

Иногда можно слышать и высказывания такого рода: "Ему лет

35-40, по крайней мере не больше 45". Очевидно, что доверитель-

ный интервал (35;45) имеет большую доверительную вероятность,

чем интервал (35;40). Однако интервальная оценка (35;40) более ин-

формативна, чем оценка (35;45).

276

Ц.З.

ОЦЕНКИ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ

14.3. Оценки математического ожидания

нормального распределения

В этом разделе мы рассмотрим конкретный пример построения то-

чечной и интервальной оценок. И здесь, как и ранее, исходными

данными являются результаты наблюдений

Х\,

X2,

. . . ,

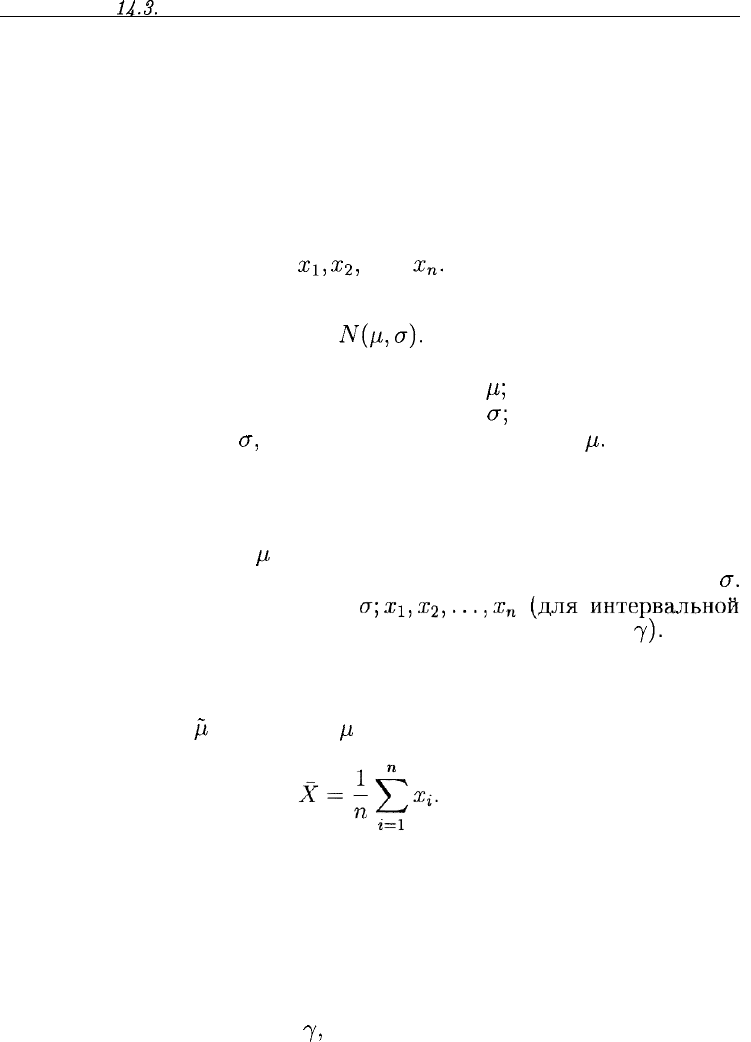
Кроме того, известно, что эти числа являются реализациями нор-

мальной случайной величины

М(/л,а).

Далее вопрос может быть поставлен различным образом:

требуется оценить неизвестный параметр //;

требуется оценить неизвестный параметр

а;

известен параметр

а,

требуется оценить параметр

ц.

Из перечисленных трех задач мы рассмотрим лишь одну — послед-

нюю.

Итак, требуется найти точечную и интервальную оценки мате-

матического ожидания

fj,

случайной величины X, распределенной

по нормальному закону с известным стандартным отклонением

а.

Исходными данными являются

оценки требуется еще задать доверительную вероятность

7)-

Точечная оценка

Точечную оценку

параметра

определим как эмпирическое сред-

нее:

Как уже отмечалось, такая оценка является несмещенной и состоя-

тельной для любой случайной величины, в том числе, разумеется,

и в данном случае.

Интервальная оценка

Для построения интервальной оценки необходимо сначала выбрать

доверительную вероятность

которая после этого считается задан-

ной.

Справедливо следующее утверждение: сумма независимых слу-

чайных величин, каждая из которых распределена по нормальному

277

ГЛАВА

Ц.

ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ

закону, также распределена по нормальному закону. Отсюда выте-

кает, что величина X распределена по нормальному закону.

Выше было показано (см. (1)), что

Ее распределение является нормальным с математическим ожида-

нием 0 и дисперсией 1. Пользуясь этим обстоятельством, можно по

данному

найти такое число

щ,

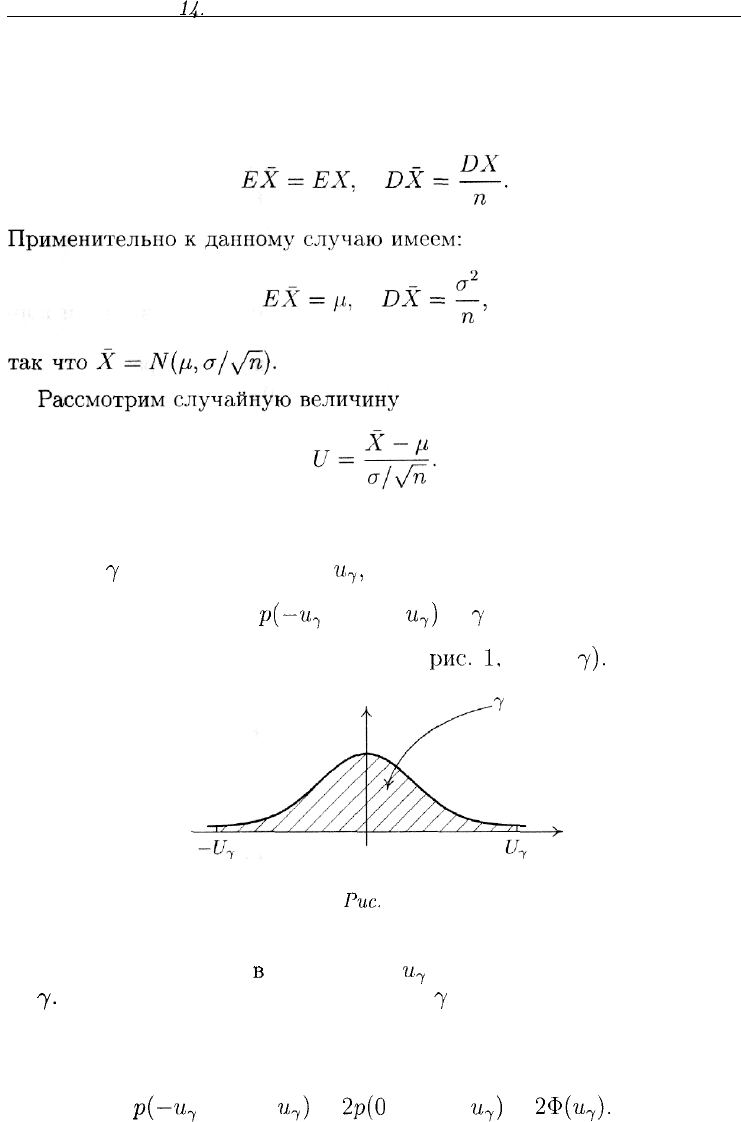
чтобы выполнялось соотношение

р(-щ

< U <

щ)

(площадь области, заштрихованной на

рис.

равна

7)-

Рис.

Замечание. Индекс 7

выражении

подчеркивает зависимость и

от

Если по контексту понятно, какое

имеется в виду, то, опуская

индекс, мы будем писать просто и.

Справедливо равенство

р{-щ

< U <

щ)

2р(0

< U <

щ)

= 2Ф(п

278

Ц.З.

ОЦЕНКИ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ

Напомним, что функция

Ф(х)

служит для вычисления вероятнос-

тей, связанных с нормальным распределением. Таблица ее значений

имеется в приложении (в конце книги).

Для нахождения числа

достаточно решить уравнение

Число

ищется по заданному числу

при помощи таблицы значе-

ний функции

Ф(ж).

Получив

мы можем утверждать, что вероятность события

—и

< U <

щ,

или, более подробно,

равна

Последнее неравенство равносильно следующему:

Таким образом, с доверительной вероятностью

математическое

ожидание

лежит в интервале

(pi,/i2),

где

fj,\

—

щ—1=,

(2)

Число

£ =

Щ-^=

(4)

называется погрешностью оценки математического ожидания. С до-

верительной вероятностью

можно считать, что оценка X отклоня-

ется от истинного значения

не более чем на е (рис. 2).

Из формулы (4) видно, что с ростом числа данных п погрешность

становится все меньше, т. е. доверительный интервал сужается. В

279

свою очередь, чем меньше погрешность, тем больше данных необ-

ходимо собрать для ее достижения. Если требуемая погрешность е

задана, то можно найти соответствующий объем данных:

(5)

При этом, разумеется, п должно быть целым числом. Так как сбор

данных часто связан с некоторыми затратами, обычно берут мини-

мальное целое п, удовлетворяющее неравенству (5).

Пример 2. При измерении нормальной случайной величины со

стандартным отклонением, равным 5, и неизвестным математиче-

ским ожиданием

(л

получена следующая выборка:

3, 12, 8, 14, 15, 6, 19, 10, 15, 6.

Требуется найти: 1) интервал, содержащий параметр /i с довери-

тельной вероятностью

0,95; 2) погрешность оценки X, соответ-

ствующую этой доверительной вероятности.

В данном случае

5, п = 10,

= 0,95.

Для точечной оценки получаем

- 3 + 12 + 8 + 14 + 15 + 6 + 19 + 10 + 15 + 6

= 10,8.

Решим уравнение

2Ф(м)

= 0,95,

ф(и)

= 0,475.

Для этого следует найти число 0,475 или ближайшее к нему в табли-

це среди значений функции

Ф(х)

(таблица дана в приложении). Бли-

жайшее число — 0,477. Соответствующее ему значение аргумента

= 2,0.

280