Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

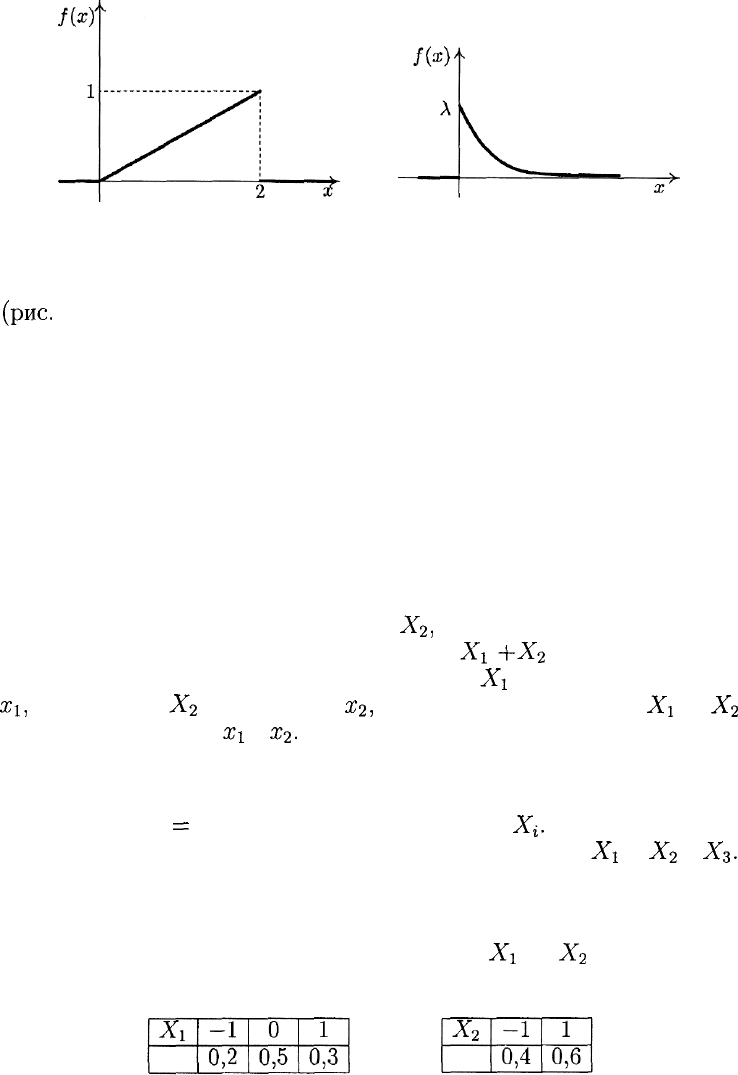
12.6. СУММА СЛУЧАЙНЫХ ВЕЛИЧИН

Рис. 6

Рис. 7

(рис.

7). Здесь Л — некоторое положительное число. Показательное

распределение применяется в теории массового обслуживания.

Для непрерывных распределений, как и для дискретных, мож-

но рассматривать числовые характеристики: математическое ожи-

дание, дисперсию и др. Они вычисляются при помощи плотности

распределения.

12.6. Сумма случайных величин

Если в результате испытания принимают определенные значения

сразу две случайные величины, Х\ и

то их можно рассматривать

вместе. В частности, определим их сумму

Х\

следующим обра-

зом: если в результате испытания величина

Х\

принимает значение

х\,

а величина

— значение

то случайная величина

Х\

принимает значение

х\

Х2-

Аналогично определяется сумма п случайных величин.

Пример 11. Студент сдает в сессию три экзамена. Оценка по г-

му экзамену (Г

1,2,3) — случайная величина

Тогда общая сум-

ма оценок за все три экзамена — случайная величина

Х\

Хз-

Приведем пример построения закона распределения суммы двух

случайных величин.

Пример 12. Пусть случайные величины

Х\

задаются та-

блицами распределения следующего вида:

251

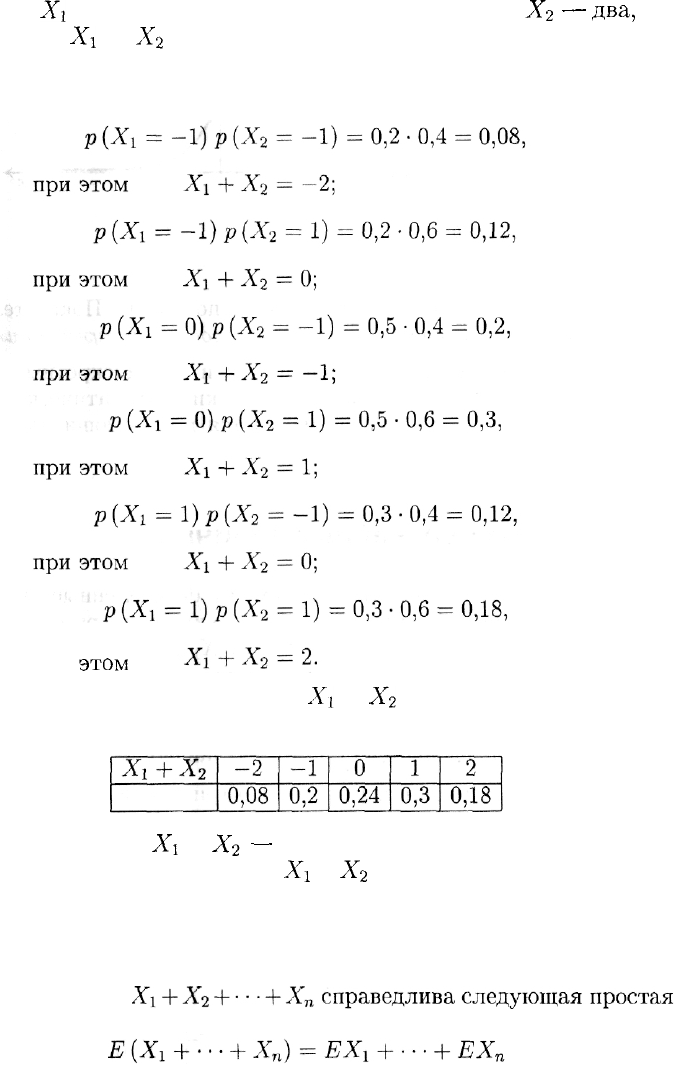
ГЛАВА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Так как

Х\

принимает три различных значения, a

—

два,

то

для суммы

Х\

получаем шесть возможностей. Выпишем их,

вычислив попутно вероятности.

Итак, определим:

при

этом

Таким образом, для величины

Х\

Хг

получаем следующую та-

блицу распределения:

Замечание 1. Если

— непрерывные случайные величины,

то закон распределения суммы

строится гораздо сложнее.

В случае суммирования п дискретных случайных величин, где

п > 2, таблица распределения строится аналогичным образом. Как

в дискретном, так и в непрерывном случаях для математического

ожидания суммы

формула:

252

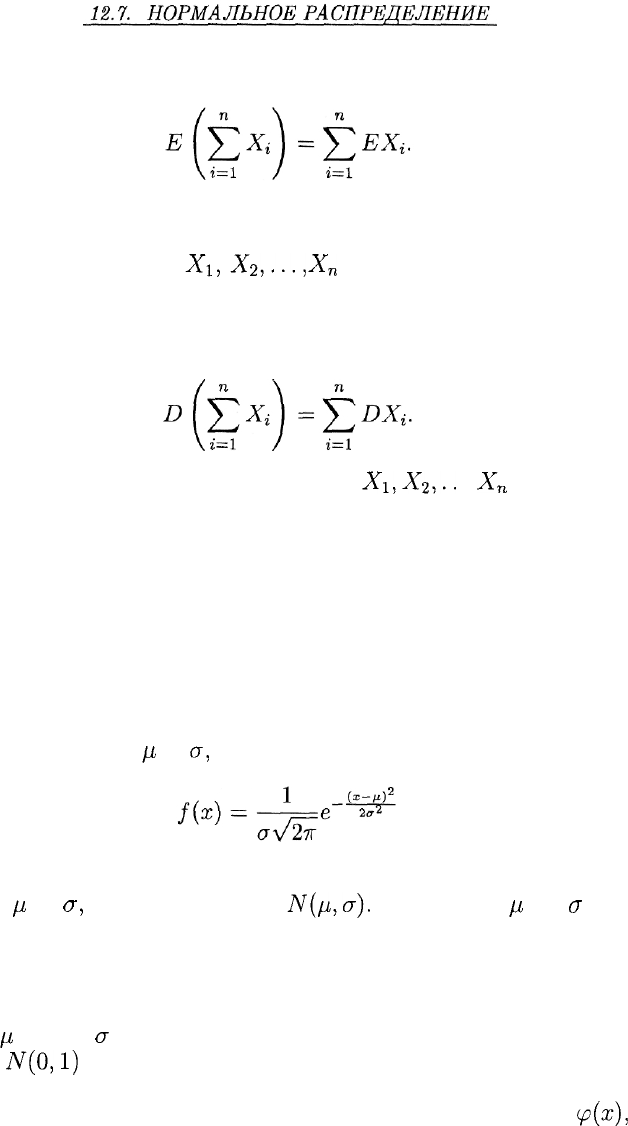
или, применяя знак сокращенного суммирования:

Аналогичная формула для дисперсии справедлива не всегда, а

только в случае независимых случайных величин.

Случайные величины

Х\,

Хг,...,

называются независимыми,

если закон распределения каждой из них не зависит от того, какие

значения приняли другие величины.

Для дисперсии суммы независимых случайных величин справед-

ливо соотношение

Замечание 2. Отметим, что величины

Xi,X

,..

•,

могут иметь

один и тот же закон распределения. В этом случае вместо термина

"независимые случайные величины" употребляют термин "незави-

симые наблюдения (испытания)".

12.7. Нормальное распределение

Наиболее часто применяется для анализа реальных ситуаций так

называемое нормальное (или гауссово) распределение. Оно зависит

от двух параметров,

а,

и задается плотностью вида

(рис. 8). Случайную величину, распределенную нормально с пара-

метрами

а,

будем обозначать

N((j,,cr).

Параметры

fj,

имеют

вполне ясный смысл: это соответственно математическое ожидание

и стандартное отклонение. Зависимость нормального распределения

от параметров мы обсудим несколько позже, сначала же рассмотрим

важный частный случай.

При

= 0 и

= 1 получается стандартное нормальное распре-

деление

N(0,1)

(напомним, что стандартной называется случайная

величина с нулевым математическим ожиданием и единичной дис-

персией). Его плотность будем обозначать особым образом,

<р(х),

253

ГЛАВА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Рис.

Рис,

исследования функции

<р(х)

достаточно рассмотреть ее для значений

0. В точке х = 0 функция

(р(ж)

имеет максимум

а с увеличением аргумента х убывает, причем это убывание проис-

ходит довольно быстро:

Перейдем к рассмотрению основной задачи — вычислению веро-

ятностей типа

р(а ^.U^b).

254

12.7.

НОРМАЛЬНОЕ

РА

ОПРЕДЕЛЕНИЕ

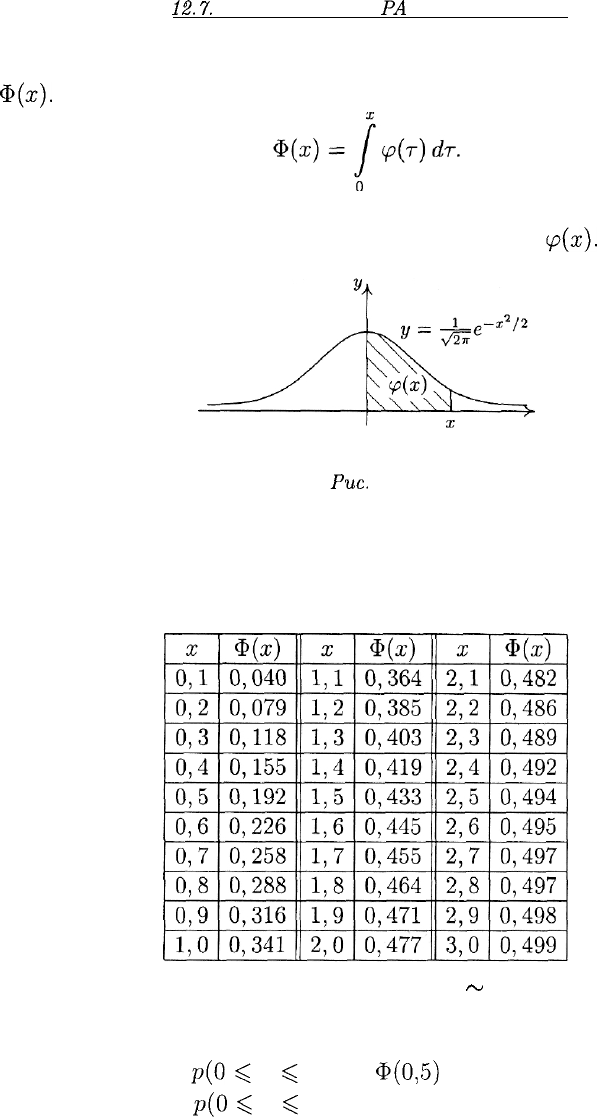
С этой целью определим для неотрицательных чисел х функцию

Ф(х).

Имеем:

Площадь фигуры, заштрихованной на рис. 10, равна Ф(х). Иначе

говоря, функция Ф(х) — первообразная функции

(р(х).

Рис.

Для вычислений, связанных с функцией Ф(х), обычно пользуются

таблицами различной степени подробности. Мы будем пользоваться

следующей таблицей (для удобства она повторена в приложении в

конце книги):

Можно считать, что при х > 3 имеем Ф(х) ~ 0,5.

При помощи этой таблицы можно сразу найти, например, следу-

ющие вероятности:

р(0

0,5) =

Ф(0,5)

= 0,192,

р(0

0,3) = Ф(0,3) = 0,118.

255

ГЛАВА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

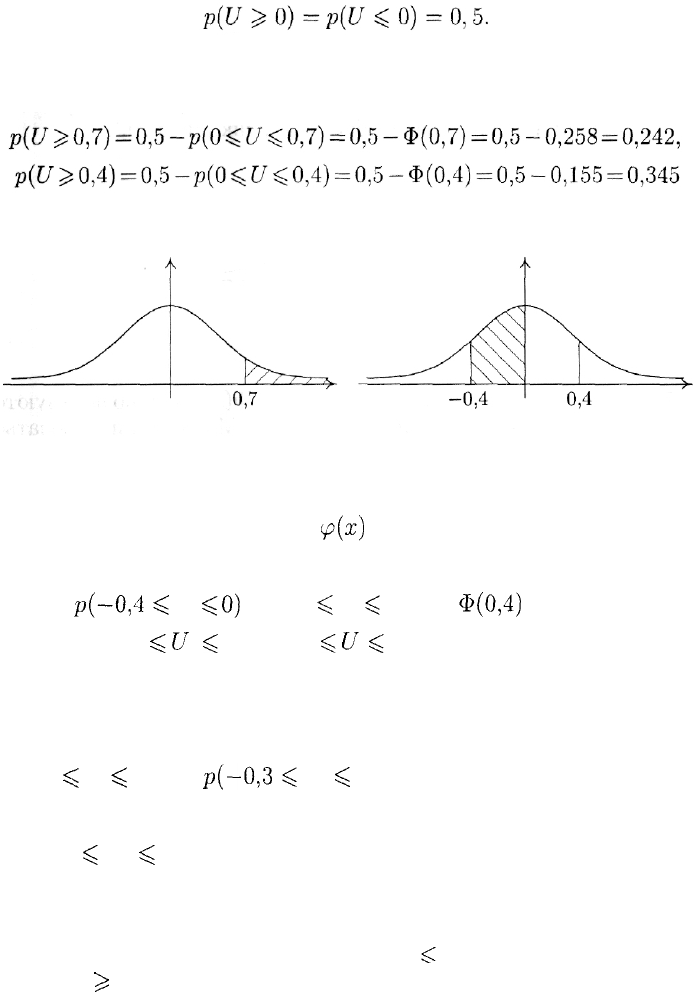
Из симметричности графика плотности распределения (рис. 9),

легко видеть, что

Поэтому

(рис. 11).

Рис. 11 Рис. 12

Поскольку график функции

ip(x)

симметричен, справедливы сле-

дующие соотношения:

р(-0,4

^ U ^

Ь)

= р(0 ^ U ^ 0,4) =

Ф(0,4)

= 0,155,

р(-0,8 ^

С/

^ 0) = р(0 ^

^ 0,8) = Ф(0,8) = 0,288

(рис. 12).

Наконец, вот еще три случая:

р(0,1 ^ U ^ 0,3) =

р(-0,3

U ^ -0,1) =

= Ф(0,3) - Ф(0,1) = 0,118 - 0,040 = 0,078,

р(-0,1 ^ U

0,3) = Ф(0,3) + Ф(0,1) = 0,118 + 0,040 = 0,158.

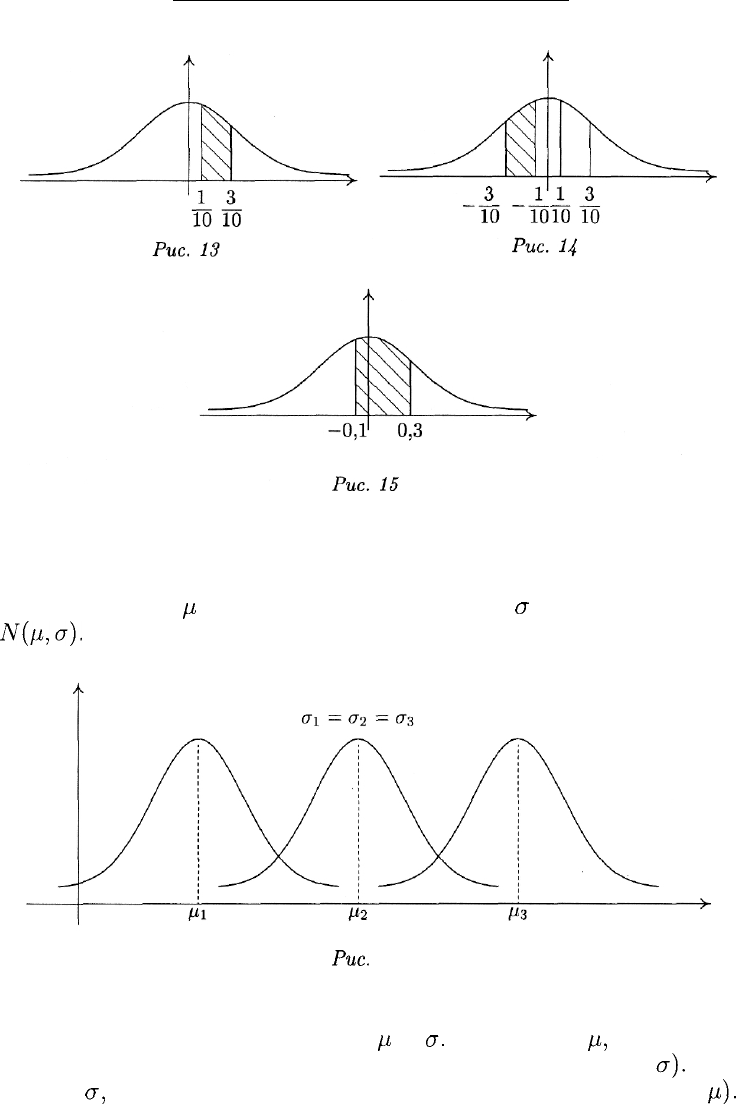
(рис. 13, 14, 15).

Замечание. Во всех этих формулах знак

§;

можно заменить на знак

<, а знак ^ — на знак >.

256

12.7. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Перейдем теперь к рассмотрению нормального распределения об-

щего вида. Напомним, что нормальное распределение с математиче-

ским ожиданием

и стандартным отклонением

обозначается через

N{fi,a).

Рис.

На рис. 16, 17 показано, как график плотности нормального рас-

пределения зависит от параметров

а.

Чем больше

/л,

тем правее

расположена наивысшая точка графика (при одинаковых

а).

Чем

больше

а,

тем более пологим является график (при одинаковых

/л).

257

ГЛАВА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Рис.

Пусть имеется случайная величина X —

iV(/x,

ст). Вычисление ве-

роятностей типа р(а ^ X ^

Ь)

сводится к вычислению аналогичных

вероятностей для стандартной величины U =

N(0,1).

Именно: ока-

зывается, что линейные операции над нормальной случайной вели-

чиной приводят опять к нормальной случайной величине (с другими

числовыми характеристиками). Для нас сейчас важно то, что, отни-

мая от

нормальной

случайной величины ее математическое ожи-

дание и деля на стандартное отклонение, получаем в результате

стандартную нормальную величину

Поэтому

Аналогично

258

12.7. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

В частности, для некоторых конкретных значений получаем:

Приведем еще один пример.

Пример 13. Вес пачек с рисом, расфасованных фирмой "Новый

рис", является нормально распределенной случайной величиной с

математическим ожиданием 1 кг и стандартным отклонением 10 г.

Какой процент пачек имеет вес:

а) от 990 г до 1020 г;

б) менее 990 г ;

в) более 1020 г?

Решение. Вес пачки риса является нормально распределенной вели-

чиной X - N(1000,10). Поэтому

Ответ: а) 81,8%; б) 15,9%; в) 2,3%.

259

ГЛАВА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Наряду с вычисленем вероятностей, связанных с нормальным

распределением, можно решать задачи и другого типа.

Пример

14-

Найти такое число С, что

р(0 < U < С) = 0,2.

Решение. Имеем:

По условию

Ф(С) - 0,2.

Обратимся к таблице значений функции Ф. Среди ее значений

нет числа 0,2. Поэтому ищем ближайшее к нему. Это число 0,192,

соответствующее значению С = 0,5.

Ответ: С = 0,5.

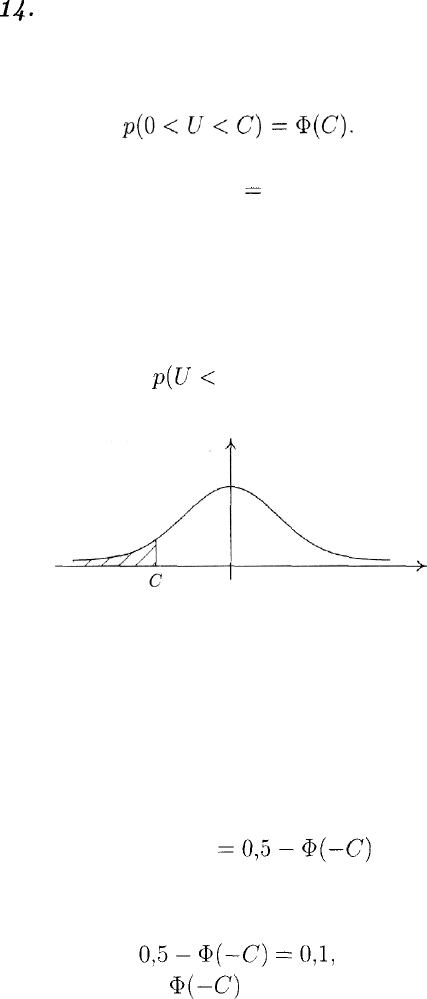
Пример 15. Найти такое число С, что

p(U<

С) = 0,1.

Рис. 18

Решение. Для любого положительного числа С выполняется нера-

венство

p(U <С)> 0,5.

Поэтому искомое значение С — число отрицательное (рис. 18). С

учетом этого получаем, что

p{U <С)

=0,5-Ф(-С)

(в качестве аргумента функции Ф указано положительное число

—С). Далее,

0,5-Ф(-С)

0,1,

Ф(-С)

=0,4.

260