Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

11.4. ПРИМЕРЫ ВЫЧИСЛЕНИЯ ВЕРОЯТНОСТЕЙ

Поэтому

(8)

Теперь осталось подставить вероятности "простых" событий

Бг.

По условию 5% изделий бракованные. Поэтому

Подставляя в формулу (8), получаем

р(А) = 0,05 • 0,95 +

0,95

• 0,05 = 0,095.

Выбираем

первое<

изделие

Выбираем

второе

изделие

Выбираем

второе

изделие

Оба изделия

бракованные

0,05 • 0,05

Бракованное только

первое изделие

= 0,05 • 0,95

Бракованное только

второе изделие

рз

= 0,95 • 0,05

Среди двух изделий

нет бракованных

= 0,95 • 0,95

Рис. 10

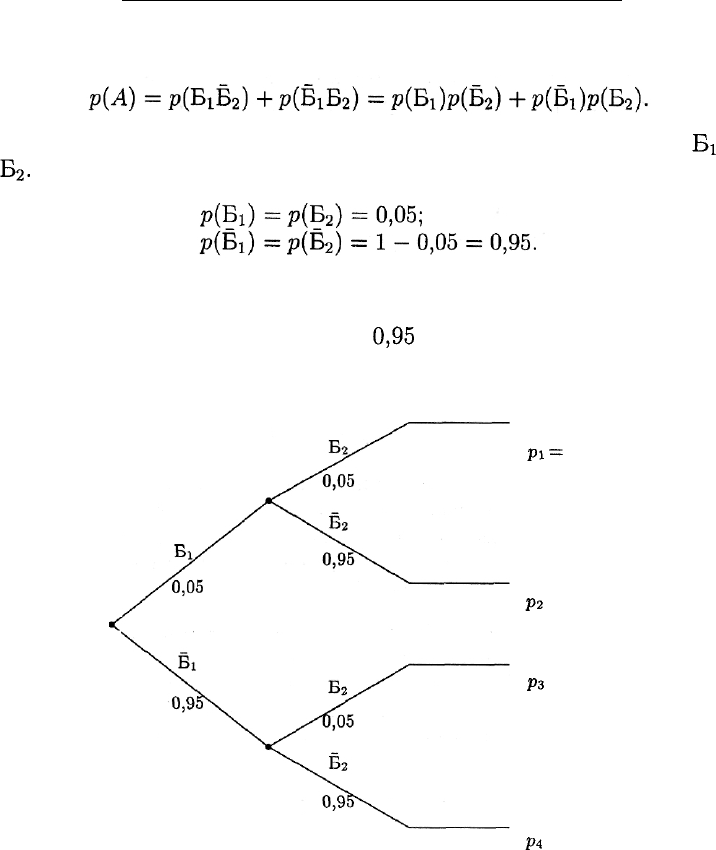
Решение 2. Построим так называемое дерево вероятностей, учиты-

вающее все возможные исходы (рис. 10). Здесь вершинам дерева

(кроме концевых) соответствуют испытания, а ребрам — события.

Сначала рассмотрим первое изделие. При этом возможны два исхо-

да — изделие может оказаться бракованным (с вероятностью 0,05)

либо качественным (с вероятностью 0,95). В каждом из этих случаев

221

ГЛАВА 11. СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТИ

рассмотрим второе изделие, которое тоже может быть либо брако-

ванным, либо качественным (с теми же вероятностями).

В результате получаем четыре возможности, обозначаемые кон-

цевыми вершинами дерева. К каждой из этих возможностей ведет

путь из начальной точки, состоящий из двух ребер дерева. Для нахо-

ждения вероятностей

Рг,Р2,Рз,Р4

перемножаются вероятности ребер

соответствующего пути.

Искомая вероятность вычисляется как сумма

рг

рз:

+Рз

0,095.

Замечание. Поскольку все возможные исходы в сумме составляют

достоверное событие, то суммарная вероятность всегда равна едини-

це. В данном случае

Пример

17.

Через остановку пролегают троллейбусный и авто-

бусный маршруты. Троллейбус подъезжает через каждые 15 минут,

автобус — через каждые 25 минут. К остановке подходит пассажир.

Какова вероятность того, что в ближайшие 10 минут на остановке

появится троллейбус либо автобус?

Решение 1. Пассажир подошел к остановке в некоторый случайный

момент между двумя последовательными приездами троллейбуса.

По условию троллейбус подъезжает через каждые 15 минут. По фор-

муле геометрической вероятности найдем вероятность р(Т) того, что

троллейбус появится на остановке в ближайшие 10 минут:

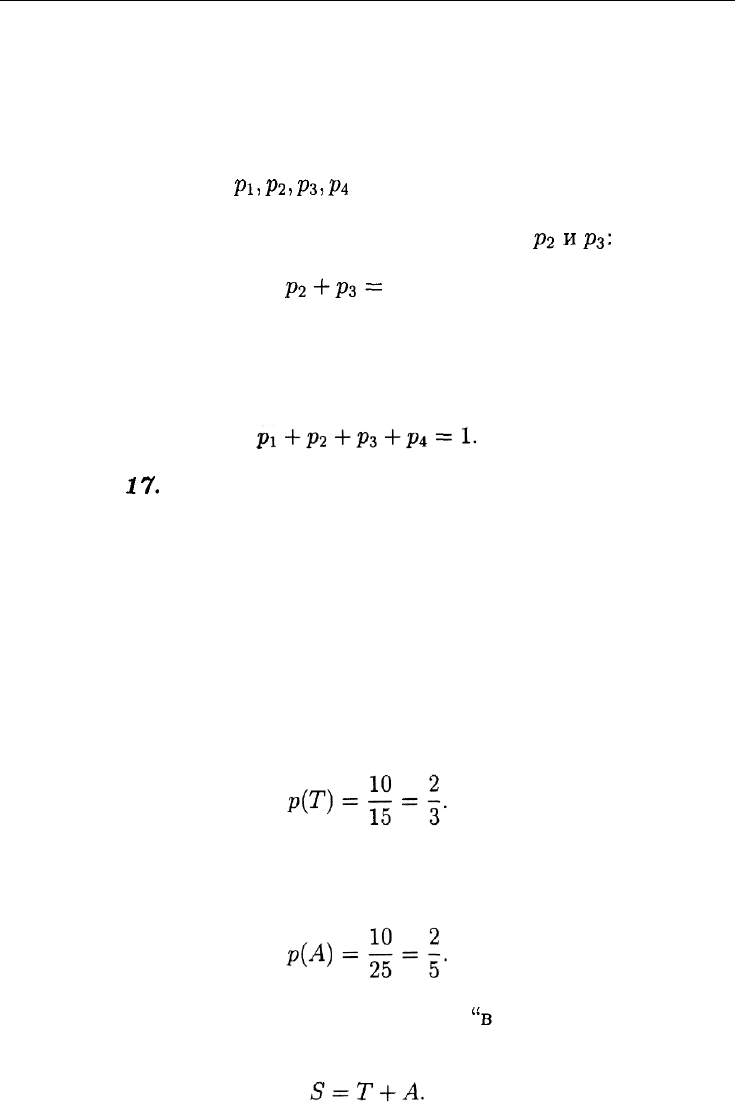
Вероятность р(А) того, что в ближайшие 10 минут на остановку

подъедет автобус, такова:

Нас интересует вероятность события S =

"в

ближайшие 10 минут

на остановку подъедет троллейбус либо автобус". Ясно, что

222

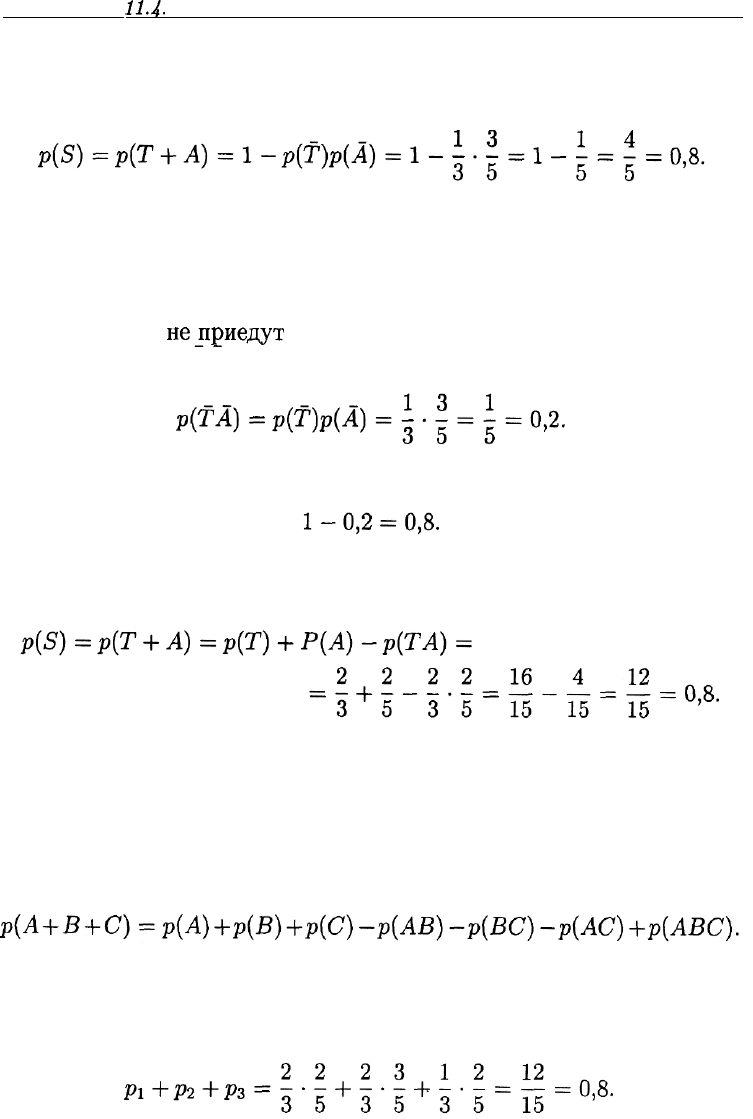
11.4-

ПРИМЕРЫ ВЫЧИСЛЕНИЯ ВЕРОЯТНОСТЕЙ

Поскольку события Т и А являются независимыми, можно вос-

пользоваться формулой (7). Имеем:

Таким образом, с вероятностью 0,8 пассажир уедет с остановки в

ближайшие 10 минут.

Замечание 1. Вместо обращения к формуле (7) можно было рассу-

ждать несколько иначе. Пассажир не уедет с остановки в ближайшие

10 минут, если

не_приедут

ни троллейбус, ни автобус, т. е. если про-

изойдет событие ТА. События Г и Л независимы, поэтому

Вероятность же того, что пассажир уедет, составляет

Замечание 2. Еще один способ рассуждений состоит в применении

формулы (1):

(Разумеется, события Т и А совместимы — могут подъехать и трол-

лейбус, и автобус.) Заметим, однако, что в случае суммы более чем

двух событий применима лишь формула (7). Хотя формула (1) и до-

пускает обобщение на случай большего числа событий, но получаю-

щиеся выражения довольно громоздки. Например, для трех событий

имеем:

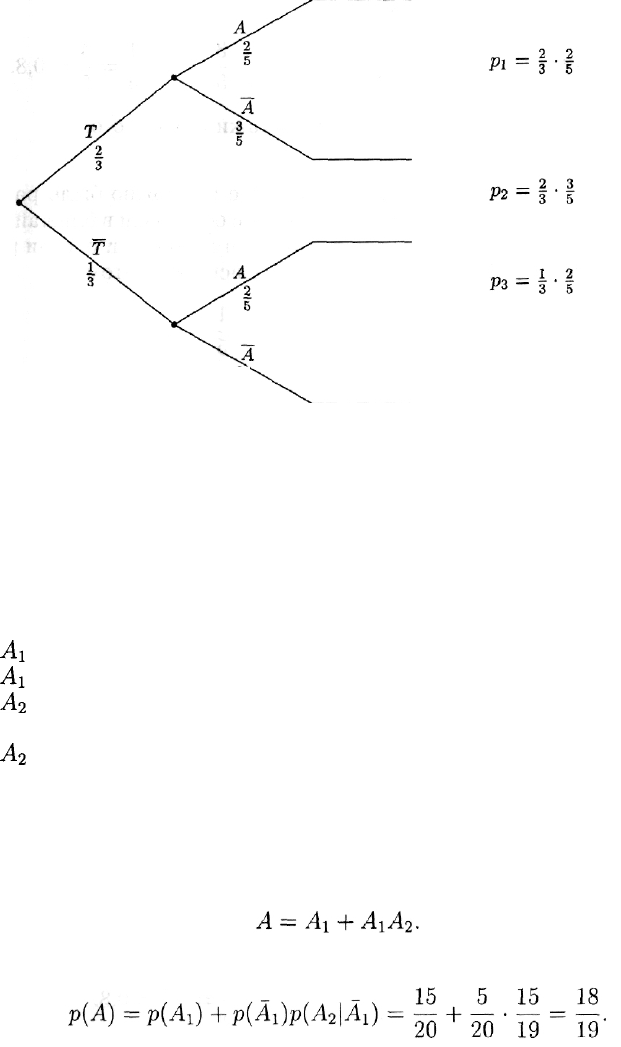
Решение 2. Построим дерево вероятностей (рис. 11). Интересующая

нас вероятность вычисляется как сумма вероятностей попарно не-

совместимых событий:

223

ГЛАВА 11. СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТИ

Подъехали и троллейбус

и автобус

(пассажир уехал)

Подъехал только троллейбус

(пассажир уехал)

Подъехал только автобус

(пассажир уехал)

Т — троллейбус подъехал

Т — троллейбус не подъехал

А — автобус подъехал

А — автобус не подъехал

Ни троллейбус, ни автобус

не подъехали

(пассажир остался)

Рис. 11

Пример 18. Студент пришел на зачет, зная 15 вопросов из 20.

Если студент не может ответить, ему предоставляется еще одна (но

не более!) попытка. Какова вероятность сдать зачет?

Решение 1. Введем следующие обозначения:

А\

- студент сразу вытянул знакомый билет (и сдал зачет);

А\

- студент вытянул незнакомый билет (еще одна попытка);

A-i

- студент со второго раза наконец-то вытянул знакомый билет

(и сдал зачет);

А^

- студент и во второй раз вытянул незнакомый билет (и ему

предстоит пересдача);

А - студент сдал зачет.

Студент сдает зачет, если он либо сразу вытянул знакомый билет,

либо сначала незнакомый, а во второй раз знакомый билет. Фор-

мально это можно записать следующим образом:

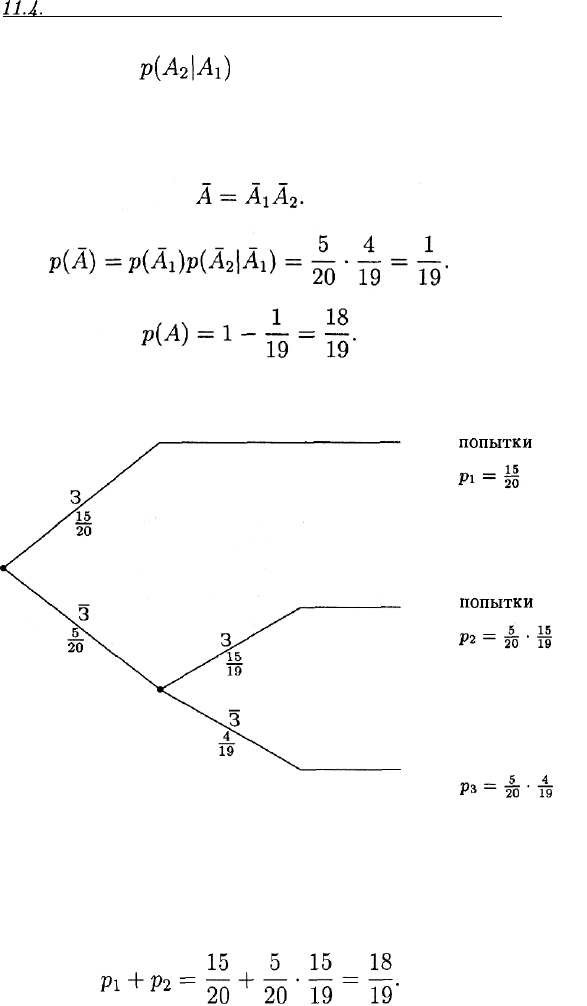
Переходя к вероятностям, получаем:

224

11.4-

ПРИМЕРЫ ВЫЧИСЛЕНИЯ ВЕРОЯТНОСТЕЙ

(Условная вероятность

p(>4.2|^4i)

равна 15/19, поскольку во второй

попытке "участвует" 19 билетов.)

Замечание. Можно было рассуждать иначе. Студент не сдает зачет,

если и в первый, и во второй раз вытянет незнакомый билет:

Поэтому

Отсюда

Первая

попытка

3 — знакомый билет

3 — незнакомый билет

Рис. 12

Зачет сдан с первой

попытки

Зачет сдан со второй

попытки

Зачет не сдан

Решение 2. Построим дерево вероятностей (рис. 12). Из него легко

получить ответ:

Пример 19. Игроки А и В разыгрывают денежный приз в сле-

дующей игре. Подбрасывается монета до тех пор, пока не выпадет

шесть "гербов" либо шесть "цифр". Если выпало шесть "гербов", то

выигрывает игрок А, если шесть "цифр" — игрок В. Монету под-

225

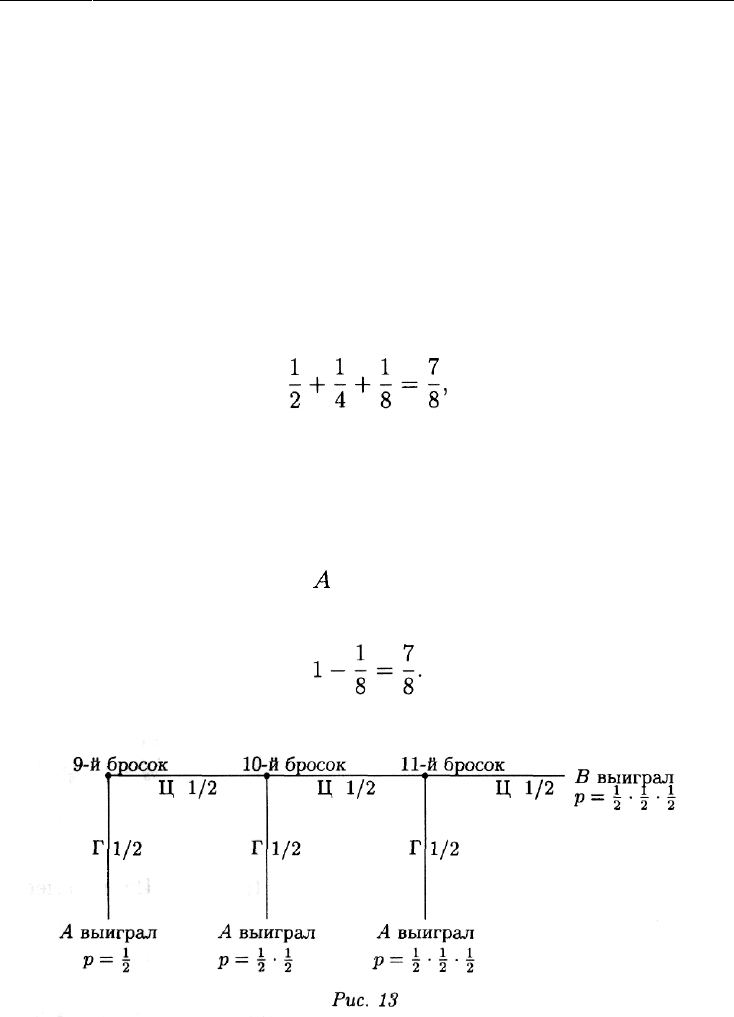
ГЛАВА 11. СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТИ

бросили 8 раз. При счете 5:3 в пользу игрока А (т. е. выпало пять

"гербов" и три "цифры") игра прервалась по не зависящим от игро-

ков причинам. В каком отношении надо поделить денежный приз?

Решение 1. Если бы игра продолжалась, ситуация могла бы раз-

виваться (начиная с девятого подбрасывания монеты) следующим

образом (приведем все возможные варианты и их вероятности):

Г - игрок А выиграл, вероятность 1/2;

Ц Г - игрок А выиграл, вероятность 1/4;

Ц Ц Г - игрок А выиграл,'вероятность 1/8;

Ц Ц Ц - игрок В выиграл, вероятность 1/8.

Таким образом, при счете 5:3 вероятность выигрыша игрока А со-

ставляет

а игрока В — всего 1/8. По-видимому, приз следует разделить в

отношении 7:1 в пользу игрока А.

Замечание. Можно было и не перебирать все возможные варианты,

а просто заметить, что игрок В выигрывает лишь в случае выпа-

дания трех цифр подряд. Вероятность этого составляет 1/8, а ве-

роятность выигрыша игрока

(что является противоположным со-

бытием, ведь ничья правилами игры не предусмотрена) составляет

соответственно

Решение 2. Дерево вероятностей см. на рис. 13. Вывод тот же, что и

в решении 1.

226

11.5. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ И ФОРМУЛА

БАЙЕСА

11.5. Формула

полной

вероятности

и формула Байеса

Одним из эффективных методов

подсчета

вероятностей является

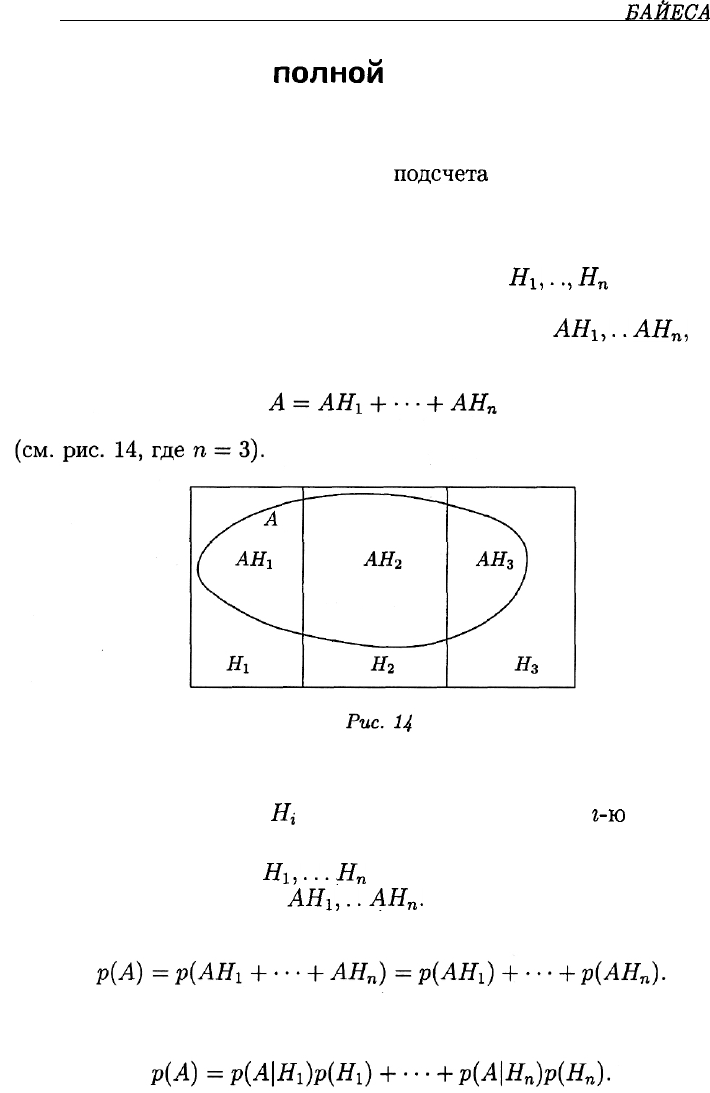
формула полной вероятности, являющаяся следствием формул для

вероятностей суммы и произведения событий.

Предположим, что событие А может наступить только вместе с

одним из попарно несовместимых событий

Hi,...

,Н

(по отноше-

нию к событию А будем называть их гипотезами). Тогда событие

А влечет за собой появление одного из событий

AHi,...,

АН

и его

можно представить в виде

Пример 20. Пусть в доме пять дверей. Событие А = "человек

вошел в дом", гипотеза

Н\

— "человек прошел через

г-ю

дверь", где

i = 1,2,3,4,5.

Поскольку события

Н\,..., Н

попарно несовместимы, то таковы-

ми же будут и события

АН

,...,

АН

Воспользовавшись формулой

(5), получаем:

Наконец, вспоминая формулу (3), можно сделать еще одно преобра-

зование:

Это и есть формула полной вероятности.

227

ГЛАВА 11. СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТИ

С формулой полной вероятности тесно связана формула Байеса,

справедливая при тех же предположениях.

Пусть опыт произведен и наступило событие А. Напомним, что

событие А могло произойти только вместе с одной из гипотез

Н\,..., Н

Поэтому можно вычислить вероятность того, что имело

место именно событие

Hi.

Эта апостериорная вероятность p(Hi\A)

отличается, вообще говоря, от априорной вероятности

p(Hi)

(в кото-

рой не учтен тот факт, что событие А произошло).

Записывая формулы для вероятности произведения событий,

имеем:

Приравняв правые части последних формул, получаем равенство

И, далее,

Привлекая формулу полной вероятности, получаем в итоге фор-

мулу

Вайеса:

Пример 21. Предположим, что 5% всех мужчин и 0,25% всех

женщин страдают дальтонизмом. Для простоты будем считать, что

мужчин и женщин одинаковое число. Какова вероятность того, что

наугад выбранное лицо страдает дальтонизмом? Если наугад вы-

бранное лицо страдает дальтонизмом, то какова вероятность того,

что это мужчина?

Решение 1. Здесь

= "выбранное лицо — мужчина",

— "выб-

ранное лицо — женщина", А = "выбранное лицо страдает дальто-

низмом". Требуется вычислить вероятности р(А) и

р(Н\\А).

Имеем:

Тогда по формуле полной вероятности

228

11.5. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ И ФОРМУЛА БАЙЕСА

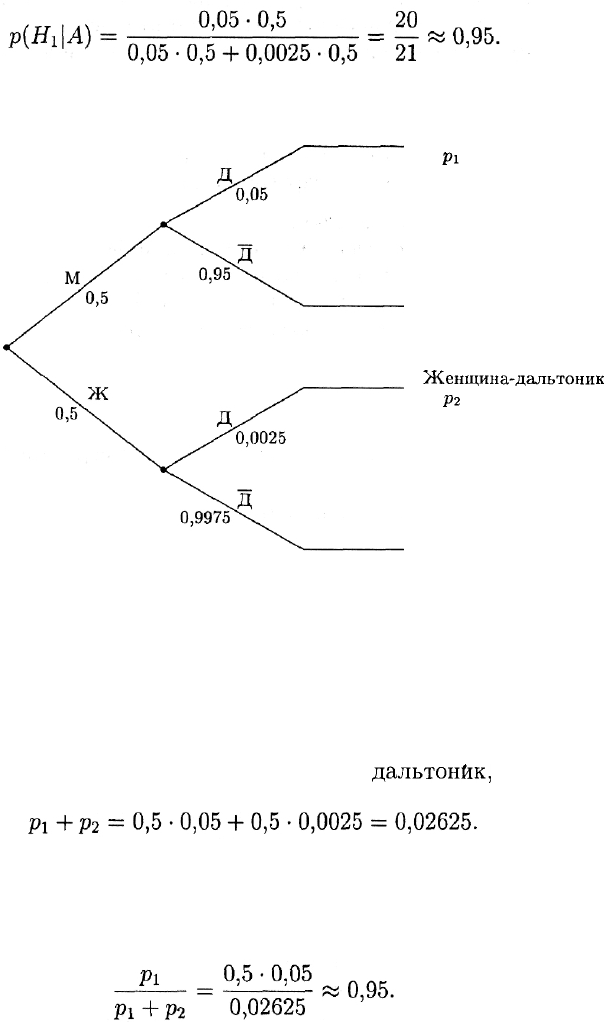
и по формуле Байеса

Случайный

выбор

Проверка

М — мужчина

Ж — женщина

Д — дальтоник

Д — не дальтоник

Мужчина-дальтоник

= 0,5

•

0,05

Женщина-дальтоник

Р2

= 0,5 • 0,0025

Рис. 15

Решение 2. Построим дерево вероятностей (рис. 15). Справа обозна-

чены лишь два исхода из четырех возможных, поскольку оставшиеся

два нас в данном случае не интересуют. Из рисунка видно, что веро-

ятность того, что наугад выбранное лицо —

дальтоник,

составляет

Если известно, что наугад выбранное лицо — дальтоник, то число

исходов сокращается с четырех до двух обозначенных. Вероятность

того, что это мужчина (условная вероятность!), равна

229

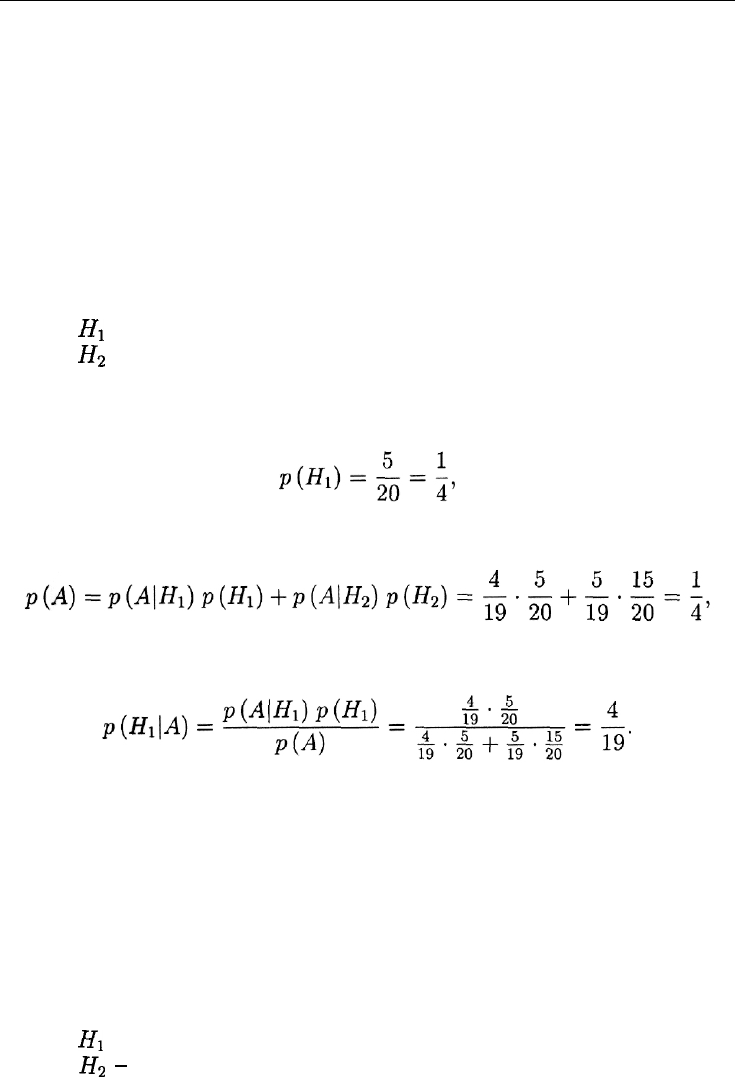
ГЛАВА 11. СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТИ

Пример 22. На экзамене студентам предлагается 20 билетов, 5

из которых легкие, а 15 — трудные. Два студента по очереди тянут

билеты — сначала первый студент, затем второй.

а) Чему равна вероятность вытянуть легкий билет для первого

студента?

б) Чему равна вероятность вытянуть легкий билет для второго

студента?

в) Известно, что второй студент вытянул легкий билет. Чему рав-

на вероятность того, что и первый вытянул легкий?

Решение. Введем обозначения:

Н\

- первый студент вытянул легкий билет;

Ич

- первый студент вытянул трудный билет;

А - второй студент вытянул легкий билет.

Тогда ответ на вопрос пункта а) дает формула классической ве-

роятности:

ответ на вопрос пункта б) — формула полной вероятности:

Пример 23. Фирма планирует выпуск на рынок нового вида то-

вара. Субъективные представления руководства фирмы таковы: ве-

роятность хорошего спроса на этот товар составляет 0,7, вероятность

плохого спроса — 0,3. Было проведено специальное исследование то-

варного рынка, которое предсказало плохой сбыт. Однако известно,

что исследования такого рода дают правильный прогноз не всегда,

а лишь с вероятностью 0,8. Каким образом маркетинговое исследо-

вание повлияло на вероятности хорошего и плохого сбыта?

Решение. Введем следующие обозначения:

- сбыт будет хорошим;

сбыт будет плохим;

А - исследование рынка предсказало плохой сбыт.

230

а ответ на вопрос пункта в) — формула Байеса: