Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие

Подождите немного. Документ загружается.

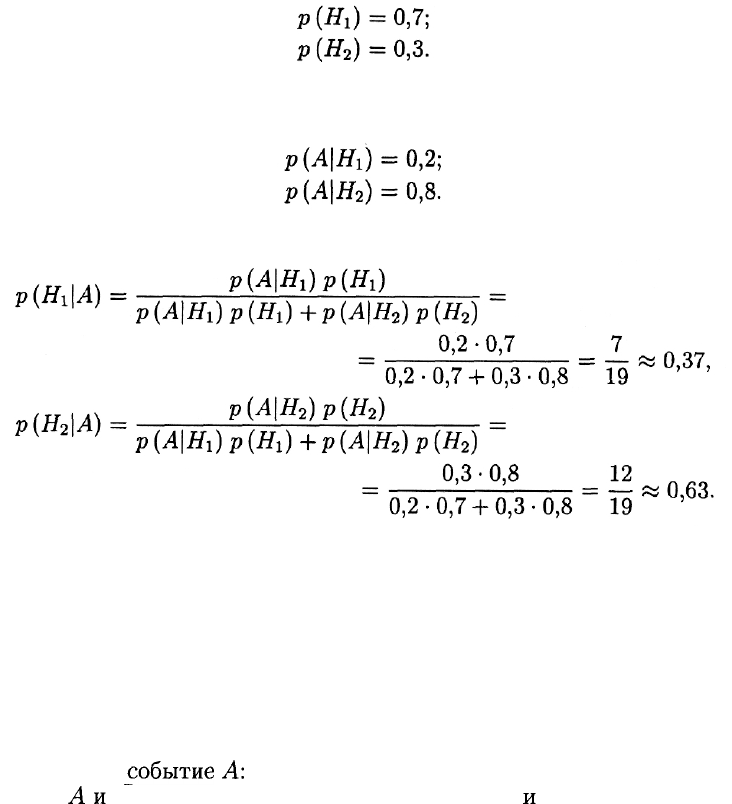
11.6. СХЕМА ИСПЫТАНИЙ БЕРНУЛЛИ

Опыт и интуиция руководства фирмы дают в соответствии с усло-

вием следующие вероятности:

Маркетинговое исследование дает верный результат с вероятно-

стью 0,8, поэтому

Подставляя все эти вероятности в формулу Байеса, получаем:

Ответ: в результате исследования вероятность хорошего сбыта

уменьшилась до 0,37, а вероятность плохого увеличилась до 0,63.

11.6. Схема испытаний Бернулли

Пусть А — случайное событие, которое может произойти в резуль-

тате некоторого испытания. Допустим далее, что нас интересует, на-

ступило ли

^обытие

А:

будем считать возможными лишь два собы-

тия —

Аи

А. Обозначим их вероятности через р

q соответственно,

р + д=1.

Предположим, что испытание повторяется при одних и тех же

условиях, скажем, три раза. В результате этого эксперимента (со-

стоящего из трех испытаний) может произойти одно из следующих

восьми событий:

ААА, ААА, ААА, ААА,

ААА, ААА, ААА, ААА

231

ГЛАВА 11. СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТИ

(запись ААА обозначает событие "в первых двух испытаниях собы-

тие А не произошло, в третьем — произошло", аналогично записаны

остальные семь событий). Подсчитаем вероятности этих событий по

формуле (6). Имеем:

Как мы видим, вероятность каждого из исходов

пред

ставима в виде

ркдЗ-к^

fc показывает число наступивших событий А, а (3 — к)

соответственно число

ненаступивших.

Вероятностные схемы такого рода называются схемами Бернул-

ли или схемами биномиальных экспериментов. Эти схемы широко

применяются при анализе реальных ситуаций в тех случаях, когда

эксперимент можно считать

биномиальным,

т. е. когда

он состоит из фиксированного числа п испытаний,

в каждом из этих испытаний происходит либо не происходит не-

которое событие,

вероятность этого события одинакова в каждом испытании,

испытания независимы одно от другого.

Пример

24-

Тренированный стрелок совершает пять выстрелов

по мишени, причем все выстрелы производятся практически в одних

и тех же условиях. При этом число попаданий в "десятку" может

меняться от 0 до 5.

Пример 25. В помете, состоящем из 8 мышей, происходящих от

одних родителей, число мышей, имеющих прямую, а не волнистую

шерстку, может равняться произвольному целому числу от 0 до 8.

Пример 26. Один за другим бросают три игральных кубика.

Число выпаданий "шестерки" может принимать одно из четырех

значений: от 0 до 3 включительно.

Вероятность того, что событие А произойдет ровно к раз после п

испытаний, обозначим через

Р(р,п,к)

(ясно, что 0 ^ к ^ п).

Справедлива следующая формула:

Здесь р — это вероятность появления события

в одном испытании,

q = 1 — р, а

(читается "С из п по

/с")

называется биномиальным

232

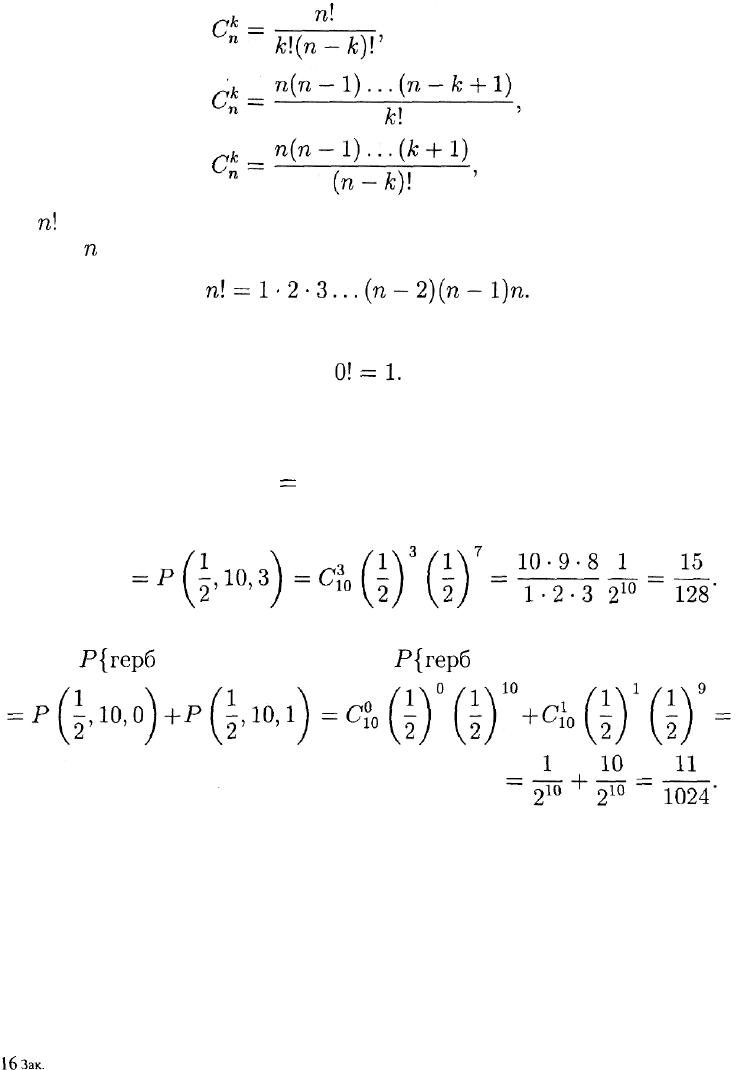
11.6. СХЕМА ИСПЫТАНИЙ БЕРНУЛЛИ

коэффициентом и вычисляется по любой из формул:

163ак.

7492

233

где

п\

(читается "п факториал") — произведение натуральных чисел

от 1 до

включительно:

Заметим также, что по определению принимается:

Пример 27. Монету бросают 10 раз. Какова вероятность того,

что при этом герб выпадет три раза? Выпадет меньше двух раз?

Решение. Здесь п — 10, р

q = 1/2.

Р{герб выпал три раза} =

Р{герб выпал меньше двух раз} =

Р{герб

не выпал ни разу} +

Р{герб

выпал один раз} =

Пример 28. Студент пишет контрольную работу по теории ве-

роятностей. У него есть предположение о том, как решить задачу,

однако свою способность найти правильное решение студент оцени-

вает невысоко — примерно числом 0,4.

Вокруг студента в аудитории сидят пять однокурсников. Можно

рискнуть опросить их и принять либо отвергнуть решение на основа-

нии большинства голосов. Подготовку этих однокурсников студент

оценивает так же, как и свою.

ГЛАВА

П.

СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТИ

Как лучше поступить студенту — положиться на свои соображе-

ния или на большинство голосов однокурсников?

Решение. Для выбора между двумя альтернативами следует снача-

ла выбрать какой-либо критерий. По-видимому, в данной ситуации

таким критерием является вероятность правильно решить задачу.

Опираясь на свои соображения, студент оценивает ее как 0,4.

Вычислим теперь вероятность того, что большинство из пяти

опрошенных однокурсников дадут правильный ответ. Большин-

ство — это либо 3, либо 4, либо 5. Поэтому искомая вероятность

вычисляется следующим образом:

Р(0,4; 5, 3) + Р(0,4; 5, 4) + Р(0,4; 5, 5) =

• (0,4)

• (0,6)

С\

• (0,4)

• 0,6 +

С\

• (0,4)

= 10 • 0,064 • 0,36 + 5 • 0,0256 • 0,6 + 0,010 24 = 0,317 44.

Вероятность снизилось с 0,4 до 0,31744 — более чем на 20%. Вы-

вод: опрос однокурсников в данной ситуации лучше не проводить.

11.7. Задания и ответы

1. На плоскость нанесена сетка квадратов со стороной 10 см. Най-

дите вероятность того, что брошенный на плоскость круг радиусом

1 см не пересечет стороны ни одного из квадратов.

Ответ: 0,64.

2. Имеются две сумки с мячами, в каждой по 5 мячей, пронуме-

рованных от 1 до 5. Наугад вынимается по одному мячу из каждой

сумки. Какова вероятность того, что это будут мячи с номерами 2 и

5 (безразлично, какой из них из какой сумки вынут)?

Ответ: 0,08.

3. Пусть испытанием является бросание точки в единичный ква-

драт, а событием А, В, С,

попадание точки в соответствующую

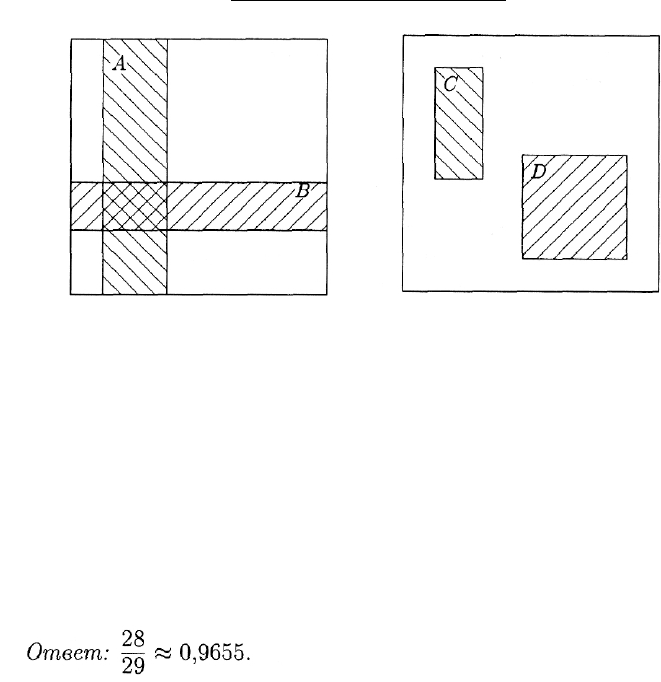
прямоугольную область (см. рис. 16, 17). Проверить совместимость

и зависимость а) событий

Аи

В (рис. 16); б) событий С и D (рис. 17).

Ответ: а) события А и В совместимы и независимы; б) события

С и D несовместимы и зависимы.

234

11.7. ЗАДАНИЯ И ОТВЕТЫ

Рис. 16

Рис. 17

4. Вероятность того, что в течение одной смены возникнет непо-

ладка, равна 0,05. Какова вероятность того, что не произойдет ни

одной неполадки за три смены?

Ответ: 0,857375.

5. Студент пришел на зачет, зная из 30 вопросов только 24. Ка-

кова вероятность сдать зачет, если после отказа отвечать на вопрос

преподаватель задает еще один вопрос?

6. Два охотника стреляют в волка, причем каждый делает по од-

ному выстрелу. Для первого охотника вероятность попадания в цель

0,7, для второго — 0,8. Какова вероятность попадания в волка (хотя

бы при одном выстреле)? Как изменится результат, если охотники

сделают по два выстрела?

Ответ: 0,94; 0,9964.

7. Из большой связки галстуков, в которой галстуки зеленого,

красного и желтого цвета находятся в пропорции 5:3:2, двое

мужчин случайным образом выбирают по одному галстуку. Какова

вероятность того, что они выберут галстуки одинакового цвета?

Ответ: 0,38.

8. Имеются две урны. В первой находится 1 белый шар, 3 черных

и 4 красных, во второй — 3 белых, 2 черных и 3 красных. Из каждой

235

ГЛАВА 11. СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТИ

урны извлекают по шару. Найти вероятность того, что цвета выну-

тых

итярои

совпадают.

Ответ:

9. На трех станках различной марки изготовляется определен-

ная деталь. Производительность 1-го станка за смену составляет 40

деталей, 2-го — 35, 3-го — 25 деталей. Установлено, что 2%, 3% и 5%

продукции этих станков соответственно имеют скрытые дефекты. В

конце смены на контроль взята одна деталь.

а) Какова вероятность того, что эта деталь нестандартная?

б) Если деталь оказалась нестандартной, какова вероятность то-

го, что она изготовлена на 1-м, 2-м или 3-м станке?

Ответ:

10. Два стрелка независимо один от другого делают по одному

выстрелу по мишени. Вероятность попадания в мишень для первого

стрелка 0,8, для второго -- 0.4. После стрельбы в мишени обнару-

жена одна пробоина. Найти вероятность того, что в мишень попал

первый стрелок.

Ответ: 6/7.

11. Как изменились бы вероятности хорошего и плохого сбыта в

примере 23, если бы исследование рынка предсказало хороший сбыт?

Ответ: вероятность хорошего сбыта — 0,9; вероятность плохого

сбыта — 0,1.

12. Игральный кубик бросают 5 раз. Найдите вероятность того,

что число очков, кратное трем, появится 2 раза.

Ответ: 80/243.

13. Всхожесть семян растений данного сорта оценивается вероят-

ностью, равной 0,8. Какова вероятность того, что из пяти посеянных

семян взойдут не менее четырех?

Ответ: 0,737 28.

Глава 12

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

12.1. Понятие случайной величины.

Закон распределения.

Биномиальная случайная величина

Мы уже знакомы с понятиями "испытание", "случайное событие",

"вероятность". Теперь приступим к рассмотрению чрезвычайно важ-

ного случая, который характеризуется следующим обстоятельством:

в результате испытания не только происходит событие, но есть еще

и возможность наблюдать некоторое число. Причем это число нас

интересует даже в большей степени, чем само событие.

Нетрудно видеть, что возможность наблюдать число часто имела

место и в тех испытаниях, которые мы уже рассматривали.

Пример 1. Бросая игральный кубик, мы получаем число точек

на верхней грани.

Пример 2. Бросая одновременно три монеты, фиксируем число

выпадений герба (это может быть 0, 1, 2 или 3).

Если каждому событию подобным образом поставлено в соответ-

ствие некоторое число, будем говорить, что задана случайная вели-

чина. Иными словами, случайная величина — это величина, прини-

мающая в результате испытания то или иное числовое значение, но

заранее неизвестно, какое именно.

Будем обозначать случайные величины большими латинскими

буквами X, Y и т. д.

237

ГЛАВА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

С каждой случайной величиной связано некоторое множество чи-

сел — значений, которые она может принимать. В результате ис-

пытания эти значения могут выпадать с различной вероятностью.

Правило, устанавливающее связь между возможными значениями

и их вероятностями (точнее, речь идет о вероятности события, за-

ключающегося в том, что случайная величина приняла то или иное

значение), называется законом распределения случайной величины.

Замечание. Случайная величина однозначно и полностью определя-

ется своим законом распределения, подобно тому как квадрат опре-

деляется длиной стороны. Переводя эту аналогию в плоскость соот-

ношения с реальным миром, заметим, что если квадрат со стороной

10 м может быть моделью дома, бассейна или детской площадки, то

случайная величина с данным законом распределения может быть

моделью числа посетителей магазина в течение дня, числа выпус-

каемых станком деталей и т. п.

Вследствие тесной связи между понятиями "случайная величина"

и "закон распределения" (или даже просто "распределение") они

часто используются как синонимы.

Перейдем теперь к рассмотрению того, каким образом может быть

задан закон распределения случайной величины, когда она прини-

мает лишь конечное число значений.

Итак, пусть случайная величина X может принимать одно из п

различных значений:

При этом каждое из этих значений величина X принимает с опреде-

ленной вероятностью — соответственно

Иными словами,

р\

— это вероятность события "случайная величи-

на X приняла значение

Xi"

или более кратко: X =

Х\,

Р2

— вероятность случайного события X =

Сведем все эти значения в таблицу

238

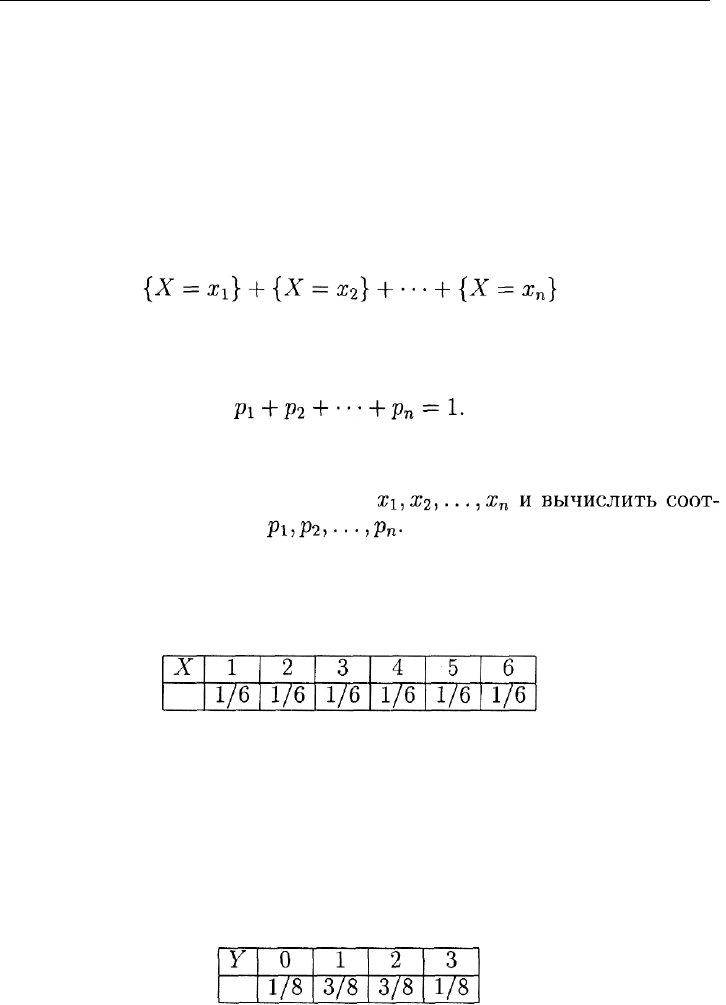
12.1. ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ. ЗАКОН РАСПРЕДЕЛЕНИЯ

в первой строке которой указаны значения, принимаемые случайной

величиной X, во второй строке — их вероятности. Она называется

таблицей распределения случайной величины X. Обычно числа в

первой строке таблицы распределения располагают в порядке воз-

растания.

Замечание. Отметим следующее важное обстоятельство. Поскольку

в результате испытания величина X наверняка примет одно из этих

значений, сумма несовместимых событий

является достоверным событием, вероятность которого равна 1. По-

этому для таблицы распределения любой случайной величины спра-

ведливо равенство

Итак, для того чтобы при решении конкретной задачи заполнить

таблицу распределения заданной случайной величины, надо выпи-

сать все принимаемые ею значения

ветствующие вероятности

Вернемся к примеру с игральным кубиком. Для упомянутой там

случайной величины (обозначим ее через X) вероятности принять

любое из шести значений равны между собой. Таблица распределе-

ния выглядит так:

Для случайной величины из примера с тремя монетами (обозна-

чим ее через Y) построить таблицу распределения несколько слож-

нее. Вспомним, что в результате одновременного бросания трех мо-

нет возможно всего 8 равновероятных исходов: ГГГ, ГГЦ, ГЦГ, ГЦЦ,

ЦГГ, ЦГЦ, ЦЦГ, ЦЦЦ. При первом исходе величина Y принимает

значение 3; при втором, третьем и пятом — значение 2; при четвер-

том, шестом и седьмом — значение 1; при восьмом — значение 0. С

учетом этого таблица распределения случайной величины Y такова:

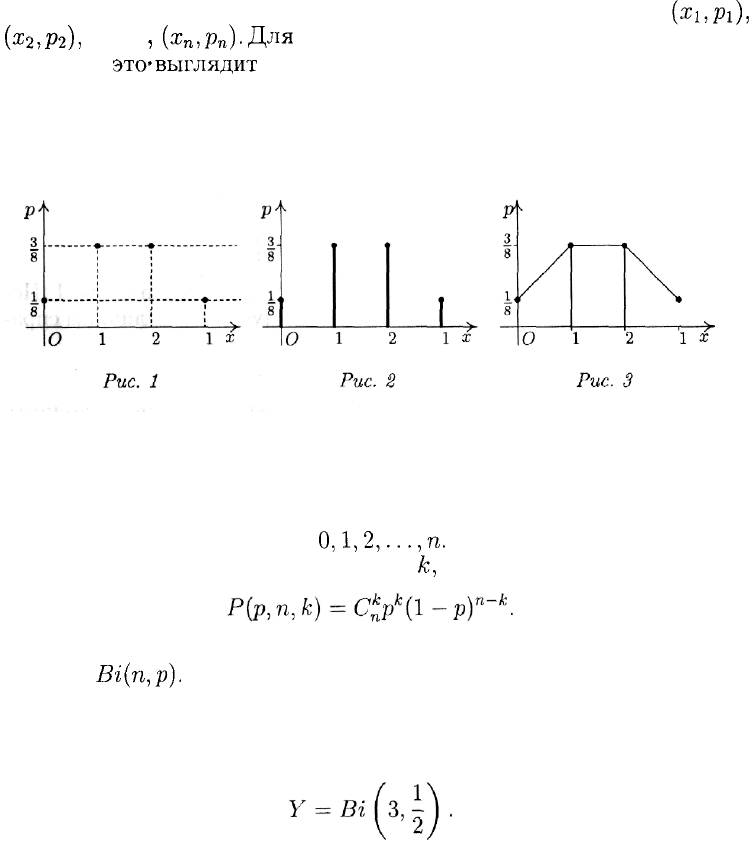
Для более наглядного представления закона распределения ча-

сто используется координатная плоскость. По оси абсцисс отмеча-

ют значения, принимаемые случайной величиной, по оси ординат —

239

ГЛАВА 12. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

их вероятности. Затем на плоскости (х,р) отмечают точки

(xi,pi),

(х2,Р2),

• • •

{xniPn)-

ля

случайной величины Y из примера с тремя

монетами

это*выглядит

так, как изображено на рис. 1. Если теперь

провести от отмеченных точек вертикальные отрезки до пересечения

с осью абсцисс, то получится столбиковая диаграмма (рис. 2). Если

же последовательно соединить точки отрезками, получится полигон

(рис. 3).

Пример 3 (схема испытаний Бернулли). Испытание пов-

торяется п раз, причем вероятность успеха в одном испытании рав-

на р.

Общее число успехов (в п испытаниях) есть случайная величи-

на, принимающая значения

0,1,2,...,п.

Вероятность того, что эта

случайная величина примет значение

к,

равна

Такую случайную величину будем называть биномиальной и обо-

значать

Bi(n,p).

Она зависит от двух параметров — п и р. Случай-

ная величина Y из примера 2 является биномиальной случайной

величиной с параметрами 3 (три монеты) и 1/2 (такова вероятность

выпадения герба у одной монеты):

12.2. Операции над случайной величиной

Пусть имеется случайная величина X, принимающая в зависимости

от результата испытания те или иные случайные значения. Если к

каждому из этих значений прибавить одно и то же число, например

3, то в результате мы получим новые числа — значения случайной

величины X + 3.

240