Шемякин Е.И., Смирнов Н.Н., Нигматулин Р.И., Натяганов В.Л. (редакторы) Газовая и волновая динамика

Подождите немного. Документ загружается.

Рис. 1.

264

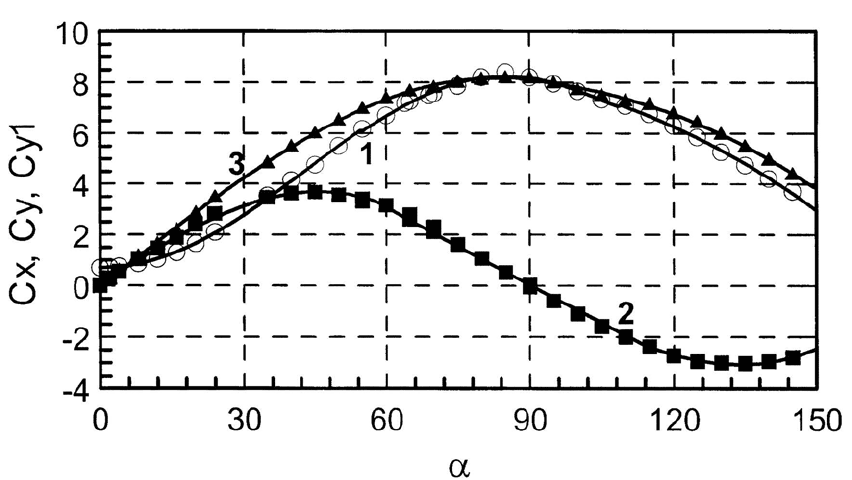
Рис. 2: Сверхзвуковое обтекание (M =1, 78), линия 1 – C

,2–C

,3–C

регистрировались интегральные силовые и моментные аэродинамические нагрузки.

Угол атаки α изменялся от 0

◦

до 145

◦

с шагом 2, 4 или 5 градусов.

Примеры некоторых фотоснимков представлены на рис. 1. При α ≈ 0

◦

− 40

◦

ударном слое всюду, кроме малой окрестности у носа модели, течение сверхзвуко-

вое. При увеличении угла атаки до 50

◦

сверхзвуковая область смещается к донному

торцу, где наблюдается течение типа Прандля-Майера. Начиная, примерно, с α =70

◦

идоα = 130

◦

поток в ударном слое на наветренной стороне дозвуковой, отрывные

зоны на подветренной стороне постепенно увеличиваются. Получены функциональ-

ные зависимости от угла атаки α стационарных аэродинамических характеристик

, C

, m

, X

,гдеC

, C

– коэффициенты сил сопротивления, подъемной

и нормальной соответственно, m

– коэффициент момента тангажа (в плоскости уг-

ла атаки) относительно центра тяжести модели, X

– координата центра давления

(аэродинамические силы отнесены к произведению скоростного напора на площадь

сечения корпуса модели, момент тангажа отнесен еще к длине модели, к которой

отнесена также координата X

). Аэродинамические характеристики C

(α), C

(α),

(α), m

(α) и X

(α) при дозвуковом (M =0, 63) и сверхзвуковом (M =1, 78)

обтекании изображены на рис. 2, рис. 3, рис. 4.

Рассмотрим некоторые особенности перечисленных характеристик рис. 2, при

числе Маха M =1, 78. Функция C

(α) (линия 1) монотонно возрастает от величины

(0) ≈ 0, 07 при α =0

◦

до C

x max

=8, 2 при α =85

◦

, при этом в интервале угла

атаки α ≈ 20

◦

− 70

◦

значение производной C

практически остается постоянным.

При α>90

◦

(α) монотонно убывает до 3,7 при α = 145

◦

. Функция C

(α) является

265

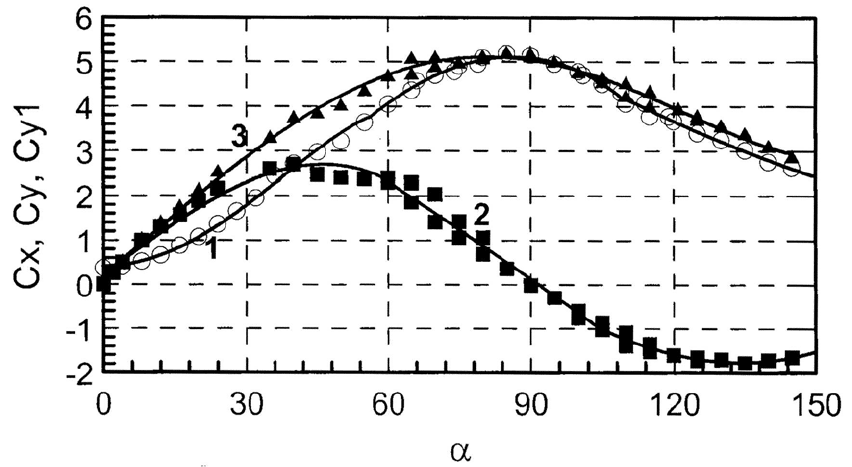
Рис. 3: Дозвуковое обтекание (M =0, 63), линия 1 – C

,2–C

,3–C

почти симметричной фигурой, относительно вертикальной прямой, α ≈ 85

◦

− 90

◦

Тенденцию смещения C

(α)

max

к α =85

◦

можно объяснить несимметричностью но-

совой и донной частей модели. Точность определения величины C

,приM>1

составляет 3-5%, при M<1 — 4-12%.

Функция C

(α) (линия 2) при α =0

◦

− 145

◦

знакопеременная в силу осесим-

метричности модели, C

(α)=0при α =0

◦

,90

◦

, 180

◦

. Значение C

y max

=3, 52

соответствует углу атаки α =45

◦

,аC

y min

≈−3, 01 —углуα = 135

◦

Коэффициент нормальной силы C

= C

sin α + C

cos α (линия 3), с увеличе-

нием a монотонно увеличивается и при α =90

◦

достигает максимального значения

y1 max

=8, 2, то есть C

y1 max

= C

x max

Зависимость

(

)

изображена (линия 3) на рис. 4 должна сравниваться с ве-

личиной X

цт

=0, 56, что характеризует степень статической устойчивости. В нашем

случае при α =0

◦

− 35

◦

∆X

= X

− X

цт

≥ 0, 08,априα<10

◦

эта величина мо-

жет превысить 0,15. При больших углах атаки α>120

◦

≥ 0, 08,априα = 145

◦

достигает 0,18. Это интервалы углов атаки, при которых испытуемая модель имеет

хороший запас статической устойчивости. В диапазоне углов 35

◦

<α<120

◦

картина

существенно меняется: по краям этого диапазона ∆X

=0, 04 − 0, 06,авсредней

части (70

◦

<α<110

◦

) ∆X

=0, 01 − 0, 02, то есть запас статической устойчивости

мал.

Важная функция m

z цт

(α) (рис. 4, линия 1), отражающая устойчивость моде-

ли, имеет немонотонный характер. С увеличением угла атаки до ≈ 35

◦

величина

z цт

| возрастает и достигает значения 0,46, затем производная m

z цт

меняет знак,

восстанавливающий момент модели уменьшается. В интервале α =80

◦

− 100

◦

—

266

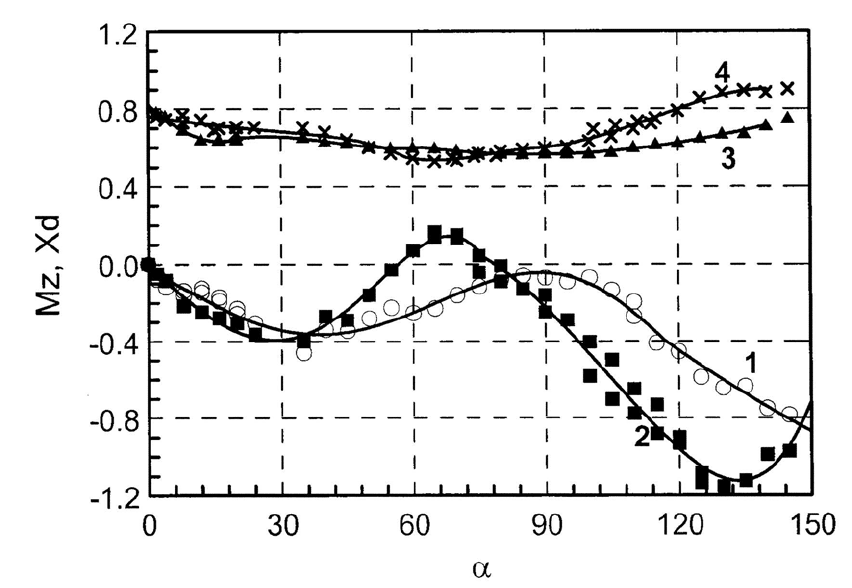
Рис. 4: Характеристики статической устойчивости при сверхзвуковом и до-

звуковом обтекании, линия 1 – m

M =1, 78,2–m

M =0, 63,3–

M =1, 78,4–X

M =0, 63

267

z цт

|≈0, 06, эффективность стабилизатора минимальна. При α = 110

◦

− 145

◦

—

z цт

| вновь возрастает, что обеспечивает устойчивость модели.

Сравнивая данные на рис. 2, рис. 3 и рис. 4, видим, что аэродинамическое харак-

теристики дозвукового и сверхзвукового обтекания модели во многом аналогичны:

симметричное расположение графика C

(α) вблизи C

x max

при α ≈ 90

◦

, такое же

свойство функции C

(α) вблизи C

y max

при α =45

◦

ивблизиC

y min

при α = 135

◦

большой запас статической устойчивости при малых углах атаки α ≤ 10

◦

и при боль-

ших углах атаки α ≥ 120

◦

; немонотонность функций m

z цт

с двумя минимальными

значениями и одним максимальным. Количественные различия можно охарактери-

зовать тем, что отношения абсолютных значений силовых функций C

, C

при

α =0

◦

, в точках максимума, минимума и для α = 145

◦

при M>1 превышают

аналогичные величины при M<1 по абсолютной величине в 1, 5 − 1, 75 раза.

Вместе с тем различия свойств взаимодействия с телом сверхзвукового и дозву-

кового потоков приводят к ряду качественных отличий по моментной характеристике

z цт

(α):еслиприM>1 модель имеет один балансировочный угол в точке α =0

◦

z цт

< 0 во всем диапазоне α =0

◦

− 145

◦

,топриM<1 – три балансировочных

угла (при α =0

◦

;57

◦

и78

◦

), при переходе через которые функция m

z цт

(α) меняет

знак, поэтому в диапазоне углов атаки 57

◦

<α<78

◦

модель неустойчива, рис. 4,

линия 2.

Подводя итоги анализа данных по первой части исследования, касающегося ста-

ционарных аэродинамических характеристик и их зависимости от двух параметров

(M и α) в широком диапазоне изменения, можно сформулировать следующее заклю-

чение: чтобы модель с хвостовым стабилизатором типа исследованной была стати-

чески устойчива во всем диапазоне углов атаки от α =0

◦

до α = 180

◦

и диапазонах

чисел Маха [0 <M≤ 0, 8], [1, 5 ≤ M ≤ 3, 0] необходимо или усилить тормозные

свойства стабилизатора (увеличить размах и площадь решеток) или менять центров-

ку модели, смещая центр тяжести вперед к носу.

2. Для получения данных о нестационарных аэродинамических характеристиках

тел использовался экспериментальный метод свободных колебаний, при котором мо-

дель закрепляется в аэродинамической трубе на поперечной оси, проходящей через

заданный центр масс, и, таким образом, имеет одну степень свободы в плоскости

угла атаки α,рис.5.

Так же как и m

, производная m

может существенно зависеть от угла баланси-

ровки модели в потоке, поэтому в экспериментах изменяли угол балансировки α = α

модели, управляя размещением дополнительных противовесов и упругих элементов.

Схема проведения испытаний была следующей. Модель в маятниковом подвесе

устанавливается неподвижно под заданным начальным углом атаки α = α

спо-

мощью механического фиксатора. При достижении заданных параметров потока в

рабочей части трубы срабатывает электромеханический расчековщик и модель по-

лучает одну степень свободы в плоскости угла атаки. Процесс угловых колебаний

модели регистрируется в памяти ЭВМ в виде цифрового файла, на рис. 6 дан пример

соответствующей осциллограммы.

При анализе осциллограмм затухающего процесса колебаний модели осуществ-

268

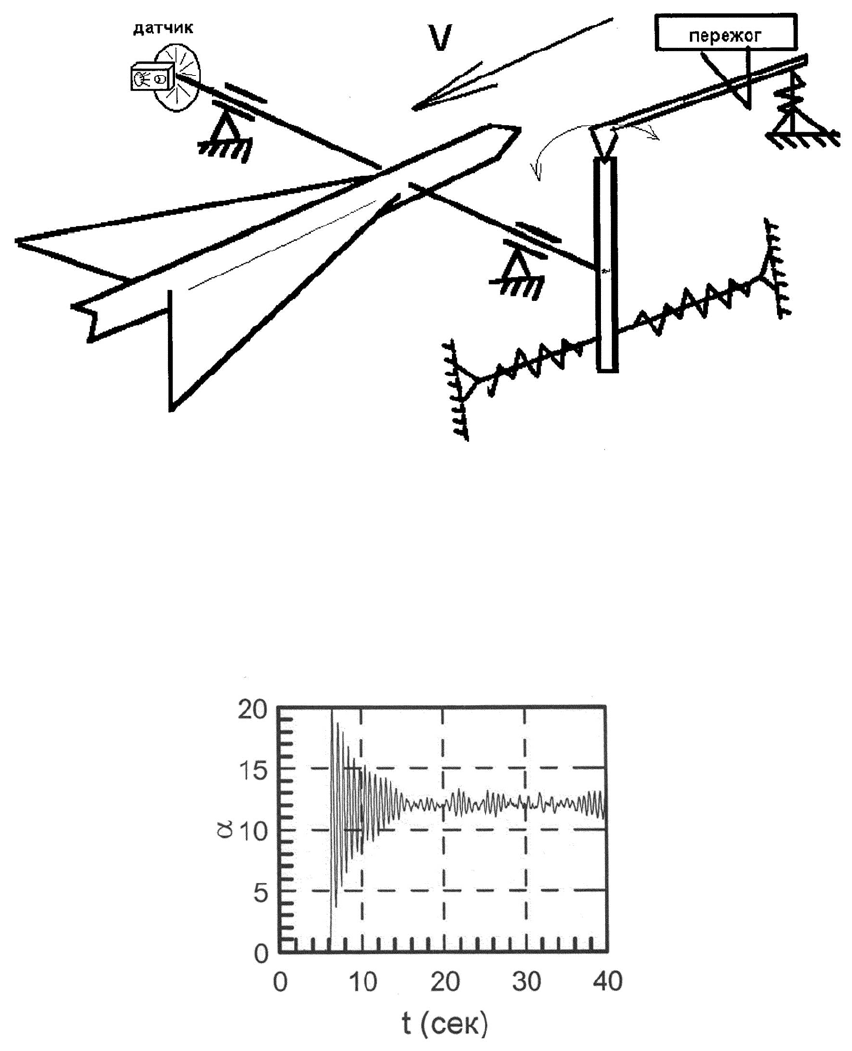
Рис. 5.

Рис. 6.

269

Рис. 7.

Рис. 8: Линия 1 – C

M =1, 78,2–C

M =0, 63,3–m

M =0, 63

270

лялось отфильтровывание паразитного вклада сухого трения в оси подвеса маятни-

ка [7]. В итоге были определены вращательные производные m

(α

) при различных

углах балансировки |α

| < 20

◦

Вместе с тем следует иметь в виду, что вращательные производные это не един-

ственный механизм демпфирования колебаний тела по углу атаки на траектории

полета. В случае оперенных тел, обладающих высокими несущими свойствами, вра-

щательные производные могут оказаться вообще не главной причиной аэродинами-

ческого демпфирования поперечных колебаний тела в полете [8].

Подставляя в уравнения движения тела (в плоскости, параллельной вектору уско-

рения земного притяжения, см. рис. 7)

˙υ = −F

sin α/m − F

cos α/m − g sin ϕ,

υ ˙ϕ = F

cos α/m − F

sin α/m − g cos ϕ,

¨α +¨ϕ = m

модель сил

ρS

+ O(α

)] · υ

ρS

(+aα

)+O(α

)] · υ

ρSL

α + m

˙α

] · υ

,ω=

˙αL

для малых углов атаки, нетрудно обнаружить, что колебания тела около центра масс

управляются квазилинейным уравнением вида:

¨α +˙α

ρSυ

2J/L



−m

− C

)



= f(α, ϕ, υ).

Здесь F

, F

– нормальная и продольная аэродинамические нагрузки на тело,

– поперечный момент, ω – безразмерная угловая скорость, L – характерный

линейный размер.

Видно, что есть два механизма демпфирования. Первый, очевидный, — связан с

вращательной производной m

, второй – возникает из-за наличия степени свободы у

центра масс, его величина не зависит от m

, а главную роль в ней играет производная

нормальной силы по углу атаки [8].

На рис. 8 изображены зависимости C

− C

при сверхзвуковом и дозвуковом

обтекании (линии1и2)иm

при дозвуковом обтекании (линия 3). Видно, что для

тел данного класса существенными являются оба механизма демпфирования.

Литература

[1] Петров К. П. Аэродинамика ракет. — М.: Машиностроение, 1977.

271

[2] Черный Г. Г. Газовая динамика. — М.: Наука, 1988.

[3] Любимов А. Н., Тюмнев Н. М., Хут Г. И. Методы исследования течений газа

и определения аэродинамических характеристик осесимметричных тел. — М.:

Наука, 1995.

[4] Миносцев В. Т., Розин А. В., Фалунин М. П. Численное и экспериментальное

исследование сверхзвукового обтекания осесимметричных оперенных тел. —

Тез. Докл. 6-го Всесоюзного съезда по по теоретической и прикладной меха-

нике, Ташкент, 1986.

[5] Краснов Н. Ф., Кошевой В. Н., Данилов А. Н. и др. Прикладная аэродинамика.

— М.: Высшая школа, 1974.

[6] Аэродинамические установки Института механики Московского университе-

та. Под ред. Черного Г. Г., Зубкова А. И., Панова. Ю.А. — М.: Изд-во МГУ,

1985.

[7] Гувернюк С. В., Зубков А. Ф., Мосин А. Ф., Павлова Е. С. Об идентифика-

циии нестационарной составляющей момента аэродинамической нагрузки на

тела с несущими поверхностями. Современные проблемы механики: Тезисы

докладов Юбилейной научной конференции, посвященной 40-летию Институ-

та механики МГУ (22-26 ноября 1999 г.), под ред. Член-корр РАН Григоряна

С. С. — М.: Изд-во Моск. ун-та, 1999.

[8] Садовничий В. А., Окунев Ю.М Модельные динамические системы одной

задачи внешней баллистики и их аналитические решения. Проблемы совре-

менной механики. Под ред. Члена-корреспондента РАН Григоряна С. С. — М.:

Изд-во Московского ун-та. 1998.

272

Проблемы моделирования горения твердых топлив в

перспективных двигательных установках

Димитриенко И. Д., Димитриенко Ю. И.

1. Введение

Разработка каждого нового класса твердых топлив всегда инициирует своеобразный

волновой процесс совершенствования техники в смежных областях: двигателестро-

ении, ракетостроении, авиастроении и космической технике. В настоящее время од-

ним из перспективных направлений разработки твердотопливных систем является

синтез композиций, у которых энергетические характеристики приближаются к ана-

логичным характеристикам жидких топлив. Разработка такого класса топлив неиз-

бежно приводит к необходимости пересмотра или как минимум изменения существу-

ющих моделей и методик расчета процессов горения топлив в составе перспективных

двигательных установок. Причиной тому является выход за традиционные темпера-

турные пределы горения в 3300 - 3500Кисоответствующие показатели по давлению

продуктов сгорания и скорости их истечения. Выход за эти пределы приводит к воз-

никновению совершенно иных физико-химических и термомеханических эффектов,

ответственных за протекание процессов горения. Назовем лишь некоторые эффекты.

Это, прежде всего, перенос тепла излучением в продуктах сгорания, вклад которого

становится значительно более существенным, а возможно даже решающим. Кроме

того, это и частичная ионизация продуктов сгорания, и турбулентное течение в зоне

протекания основных химических реакций. Кроме того, сам механизм воспламенения

твердых топлив, который, несмотря на уже многолетнюю историю его исследования,

остается до сих пор фактически «terra incognita», также требует разработки более

совершенных моделей, учитывающих микроструктурные эффекты.

В настоящей работе предложена одна из возможных моделей процесса горения

смесевых твердых топлив, учитывающая некоторые из вышеуказанных факторов.

2. Описание модели

Важнейшие элементы модели горения смесевых твердых топлив были предложены в

работах [1, 2, 3, 4, 5, 6]. Эта модель представляет собой развитие модели Зельдовича

Я. Б. [7], согласно которой процесс горения твердых топлив состоит из двух этапов:

этапа терморазложения горючего-связки и окислителя и этапа химической реакции

продуктов терморазложения в газовой фазе.

Существенно новым элементом предлагаемой модели является учет механизма

диспергирования смесевого топлива, которое вызывается двумя факторами: внут-

рипоровым давлением газообразных продуктов терморазложения горючего и окис-

лителя внутри твердой фазы и внешним высокоскоростным потоком газа. Принци-

273