Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.

311
á) äëÿ íåïðåðûâíûõ ñëó÷àéíûõ âåëè÷èí:
∫
∞
∞−
⋅⋅=
.
)( )(
dxxfxXM
Çäåñü f (x) äèôôåðåíöèàëüíàÿ ôóíêöèÿ ðàñïðåäåëåíèÿ ÑÂ.
Ñâîéñòâà ìàòåìàòè÷åñêîãî îæèäàíèÿ (ÌÎ):
1. ÌÎ ïîñòîÿííîé ðàâíî åé ñàìîé:
Ì (Ñ) = Ñ.
2. Ïîñòîÿííûé ìíîæèòåëü ìîæíî âûíîñèòü çà çíàê ÌÎ:
Ì (K · X) = K · Ì (X).
3. ÌÎ ñóììû äâóõ ñëó÷àéíûõ âåëè÷èí, ÿâëÿþùèõñÿ ôóíêöèåé
îäíîãî ñëó÷àéíîãî ñîáûòèÿ À, ðàâíî ñóììå ìàòåìàòè÷åñêèõ îæè-
äàíèé ýòèõ ÑÂ:
Ì (X ± Y) = Ì (X) ± Ì (Y).
4. ÌÎ ïðîèçâåäåíèÿ âçàèìíî íåçàâèñèìûõ ñëó÷àéíûõ âåëè-
÷èí ðàâíî ïðîèçâåäåíèþ èõ ÌÎ:
Ì (X · Y) = Ì (X) · Ì (Y).
5. Ñâîéñòâà 3 è 4 ìîæíî ðàñïðîñòðàíèòü íà ëþáîå ÷èñëî ñëà-
ãàåìûõ èëè ñîìíîæèòåëåé.
Äèñïåðñèåé ñëó÷àéíîé âåëè÷èíû Õ íàçûâàåòñÿ ìàòåìàòè÷åñ-
êîå îæèäàíèå êâàäðàòà îòêëîíåíèÿ Ñ îò åå ìàòåìàòè÷åñêîãî
îæèäàíèÿ:
à) äëÿ äèñêðåòíîé ÑÂ:
∑
⋅−=
i
ii
pXMxXD
;
2
))(( )(
á) äëÿ íåïðåðûâíîé ÑÂ:
.
)())(( )(
2
∫
∞
∞−
⋅−=
dxxfXMxXD
Äèñïåðñèÿ ðàâíà ðàçíîñòè ìåæäó ìàòåìàòè÷åñêèì îæèäàíèåì
êâàäðàòà ÑÂ Õ è êâàäðàòîì åå ìàòåìàòè÷åñêîãî îæèäàíèÿ, ò.å.
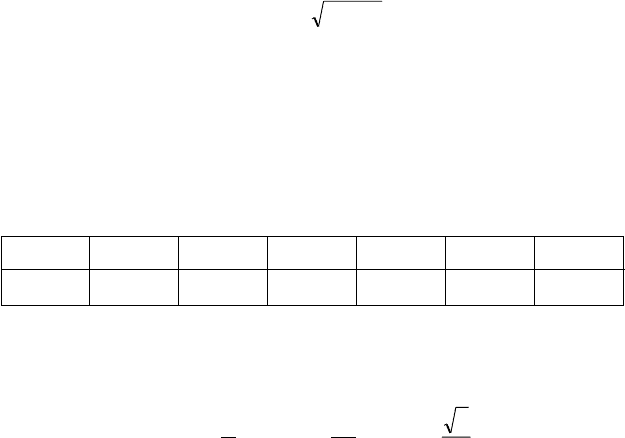
D (X) = Ì (X
2
) [Ì (X)]
2
.
312
Ñâîéñòâà äèñïåðñèè:
1. Äèñïåðñèÿ ïîñòîÿííîé ðàâíà íóëþ:
D (C) = Ì (C
2
) [Ì (C)]
2
= C
2
(C)
2
= 0.
2. Ïîñòîÿííûé ìíîæèòåëü ìîæíî âûíîñèò çà çíàê äèñïåðñèè,
âîçâîäÿ åãî â êâàäðàò:
D (K · X) = K
2
· D (X).
3. Äèñïåðñèÿ ñóììû èëè ðàçíîñòè äâóõ íåçàâèñèìûõ ÑÂ ðàâíà
ñóììå èõ äèñïåðñèé:
D (X ± Y ) = D (X) + D (Y).
4. Äèñïåðñèÿ ñóììû ÑÂ ñ ïîñòîÿííîé ðàâíà äèñïåðñèè ÑÂ:
D (X + C ) = D (X) + D (C) = D (X) + 0 = D (X).
5. Ñâîéñòâà 3 è 4 ìîæíî ðàñïðîñòðàíèòü íà ëþáîå ÷èñëî ñëà-
ãàåìûõ.
Êâàäðàòíûé êîðåíü èç äèñïåðñèè íàçûâàåòñÿ ñðåäíèì êâàä-
ðàòè÷åñêèì îòêëîíåíèåì ñëó÷àéíîé âåëè÷èíû:
.
)( )(
XDX =
σ
Èñïîëüçîâàíèå
σ
(Õ) ïîëåçíî áëàãîäàðÿ îäèíàêîâîé ðàçìåð-
íîñòè åãî ñ ðàçìåðíîñòüþ ìàòåìàòè÷åñêîãî îæèäàíèÿ.
6.3.3. Äèñêðåòíûå ðàñïðåäåëåíèÿ
Ãåîìåòðè÷åñêîå ðàñïðåäåëåíèå
Äèñêðåòíàÿ ÑÂ ñ ðÿäîì ðàñïðåäåëåíèÿ
x 123n
pP (1) P (2) P (3) P (n)
ãäå P (n) = P · q
n1
, q = 1 P, 0 < P < 1, P ïîñòîÿííîå ÷èñëî,
èìååò ãåîìåòðè÷åñêîå ðàñïðåäåëåíèå.
Åñëè Õ èìååò ãåîìåòðè÷åñêîå ðàñïðåäåëåíèå, òî
,
1
)(
p
XM =
,
2
)(
p
q
XD =
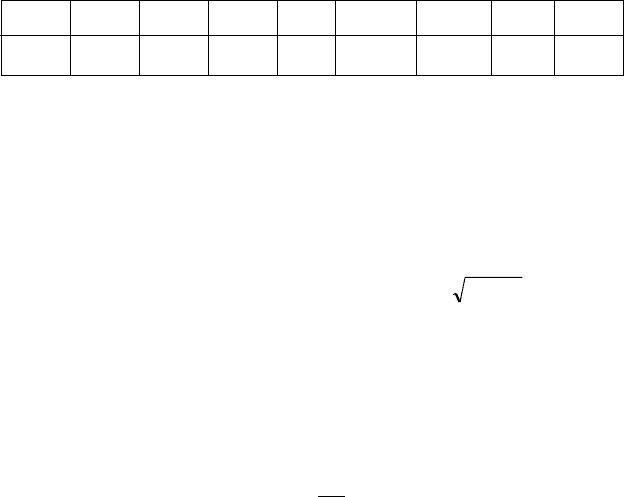
.
)(
p
q
X =
σ
313
Áèíîìèàëüíîå ðàñïðåäåëåíèå
Ïóñòü n íåêîòîðîå íàòóðàëüíîå ÷èñëî, 0 < p < 1, q = 1 p.
Äèñêðåòíàÿ ÑÂ ñ ðÿäîì ðàñïðåäåëåíèÿ
x 012k n ...
pp (0) p (1) p (2) p (k)p (n) ...
ãäå
,
)(
knkk
n
q
p
CkP
−
⋅⋅=
èìååò áèíîìèàëüíîå ðàñïðåäåëåíèå.
Åñëè Õ ñëó÷àéíàÿ âåëè÷èíà, ðàâíàÿ ÷èñëó ïîÿâëåíèé íåêî-
òîðîãî ñîáûòèÿ A â n íåçàâèñèìûõ èñïûòàíèÿõ (p = p (A) âåðî-
ÿòíîñòü ïîÿâëåíèÿ ñîáûòèÿ À â îäíîì èñïûòàíèè), òî Õ èìååò
áèíîìèàëüíîå ðàñïðåäåëåíèå.
Åñëè ÑÂ Õ èìååò áèíîìèàëüíîå ðàñïðåäåëåíèå, òî
M (X) = n · p, D (X) = n · p · q,
.
)(
qpnX ⋅⋅=
σ
Ðàñïðåäåëåíèå Ïóàññîíà
Ðàñïðåäåëåíèåì Ïóàññîíà íàçûâàåòñÿ ðàñïðåäåëåíèå äèñêðåò-
íîé ÑÂ, âåðîÿòíîñòè çíà÷åíèé êîòîðîé âû÷èñëÿþòñÿ ïî ôîðìóëå
Ïóàññîíà:
,
!
)(
λ
λ
−
=
e
m
mP
m
n
ãäå
λ
= n · p ñðåäíåå ÷èñëî ïîÿâëåíèé ñîáûòèÿ.
Äëÿ ðàñïðåäåëåíèÿ Ïóàññîíà
M (X) =
λ
è D (X) =
λ
.
Ýòî ñâîéñòâî ïðèìåíÿþò íà ïðàêòèêå ïðè ðåøåíèè âîïðîñà:
ïðàâäîïîäîáíà ëè ãèïîòåçà î òîì, ÷òî ñëó÷àéíàÿ âåëè÷èíà Õ ðàñ-
ïðåäåëåíà ïî çàêîíó Ïóàññîíà?
Ïðèìåð 6.23. Âåðîÿòíîñòü ñäàòü çàêàç â àòåëüå ðàâíà p < 1,0.
Íàñòîé÷èâûé êëèåíò îáõîäèò âñå èìåþùèåñÿ â ãîðîäå àòåëüå, ïîêà
íå äîáüåòñÿ óñïåõà. Êàêîâà âåðîÿòíîñòü, ÷òî åìó ýòî óäàñòñÿ íå
ðàíüøå, ÷åì ñ òðåòüåãî ðàçà, åñëè ïî ñòàòèñòèêå ñðåäíåå ÷èñëî ïî-
ïûòîê ðàâíî 5.

314
Ðåøåíèå. Ñëó÷àéíàÿ âåëè÷èíà ðàñïðåäåëåíà ïî ãåîìåòðè÷åñ-
êîìó çàêîíó. Ïîýòîìó Ì (Õ) = 5 =
p
1
, îòñþäà ð = 0,2. Íàéäåì
P (1) = ð · q
11
= 0,2 è P (2) = ð · q
21
= 0,2 · 0,8 = 0,16 âåðîÿòíîñòè
òîãî, ÷òî êëèåíò äîáüåòñÿ óñïåõà ñ ïåðâîãî è ñî âòîðîãî ðàçà ñî-
îòâåòñòâåííî.
Ñîáûòèÿ, ÷òî êëèåíò äîáüåòñÿ óñïåõà íå ðàíüøå, ÷åì ñ òðåòüå-
ãî ðàçà èëè ñ ïåðâîãî, èëè ñî âòîðîãî ðàçà, îáðàçóþò ïîëíóþ
ãðóïïó ñîáûòèé, ò.å. P (m ≥ 3) + [P (m = 1) + P (m = 2)] = 1. Îòñþäà
P (m ≥ 3) = 1 [P (1) + P (2)] = 1 (0,2 + 0,16) = 0,64.
Ïðèìåð 6.24. Íà àáîíåìåíòíîå îáñëóæèâàíèå ïîñòàâëåíî 5 òå-
ëåâèçîðîâ. Èçâåñòíî, ÷òî äëÿ ãðóïïû èç ïÿòè òåëåâèçîðîâ ìàòåìà-
òè÷åñêîå îæèäàíèå ÷èñëà îòêàçàâøèõ çà ãîä ðàâíî åäèíèöå. Åñëè
òåëåâèçîðû èìåþò îäèíàêîâóþ âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû,
òî êàêîâà âåðîÿòíîñòü, ÷òî çà ãîä ïîòðåáóåòñÿ õîòÿ áû îäèí ðåìîíò?
Ðåøåíèå. Ñëó÷àéíàÿ âåëè÷èíà ðàñïðåäåëåíà ïî áèíîìèàëü-
íîìó çàêîíó, òàê êàê èñïûòàíèÿ íåçàâèñèìû è âåðîÿòíîñòü
P (À) = const. Ïîñêîëüêó ìàòåìàòè÷åñêîå îæèäàíèå ÷èñëà îòêà-
çàâøèõ òåëåâèçîðîâ ðàâíî åäèíèöå, òî ìàòåìàòè÷åñêîå îæèäàíèå
ãîäíûõ ðàâíî:
.415)()( =−==
A
A
XMnXM
Ïàðàìåòð Ð îïðåäåëÿåòñÿ èç ôîðìóëû ìàòåìàòè÷åñêîãî îæè-
äàíèÿ, Ì (Õ) = n · p, ò.å. Ð =
5
4
= 0,8. «Ïîòðåáóåòñÿ õîòÿ áû îäèí
ðåìîíò» ñîîòâåòñòâóåò âåðîÿòíîñòè Ð
5
(n < 5), ãäå n ÷èñëî ãîä-
íûõ òåëåâèçîðîâ. Òîãäà èç àíàëèçà ïîëíîé ãðóïïû ñëó÷àéíûõ âå-
ëè÷èí Ð
5
(n < 5) = 1 Ð
5
(n = 5). Ïðè ýòîì âåðîÿòíîñòü ãîäíîñòè
âñåõ òåëåâèçîðîâ ðàññ÷èòûâàåòñÿ ïî ôîðìóëå Áåðíóëëè:
.8,0)5 ,5(
555555
5
==⋅⋅===
−
pqpCmnP
Âåðîÿòíîñòü èñêîìîãî ñîáûòèÿ ðàâíà:
Ð
n=5
(m > 5) = 1 0,8
5
= 0,67.
Çàäà÷ó ìîæíî ðåøèòü è äðóãèì ñïîñîáîì. Òàê êàê âåðîÿòíîñòü
ðåìîíòà ëþáîãî òåëåâèçîðà q = 0,2, à âåðîÿòíîñòü áåçîòêàçíîé
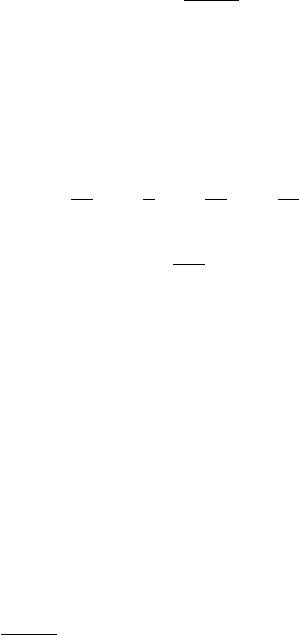
315
ðàáîòû Ð = 0,8, òî âåðîÿòíîñòü õîòÿ áû îäíîãî ðåìîíòà èç ïÿòè
òåëåâèçîðîâ ðàâíà:
Ð (À) = 1 p
5
= 1 0,8
5
= 0,67.
Ïðèìåð 6.25. Ïðèåìùèöà çà îäèí ÷àñ ïðèíèìàåò â ñðåäíåì äâå
çàÿâêè. Ïðåäïîëàãàåòñÿ ïðîñòåéøèé ïîòîê çàÿâîê. ×åìó ðàâíà
âåðîÿòíîñòü ïîñòóïëåíèÿ ÷åòûðåõ çàÿâîê çà ÷åòûðå ÷àñà?
Ðåøåíèå. Äëÿ ïðîñòåéøåãî ïîòîêà ñîáûòèé ìîæíî âîñïîëüçî-
âàòüñÿ ðàñïðåäåëåíèåì Ïóàññîíà, êîòîðîå áóäåò èìåòü âèä:
,
!
) (
)(
t
m
n
e
m
t
mP
λ
λ
−
=
ãäå ïî óñëîâèþ
λ
= 2; t = 4 è òîãäà
λ
t = 8, à m ÷èñëî çàÿâîê.
Âåðîÿòíîñòü ïîÿâëåíèÿ íå ìåíåå ÷åòûðåõ ñîáûòèé ðàññìîò-
ðèì êàê:
.9576,00424,01
3
256
3281 1
! 3
8
! 2
8
!1
8
! 0
8
1
)]3( )2( )1( )0( [1)4(
8
8
3
8
2
88
0
=−=
+++−=
=
+++−
=+++−=≥
−
−−−−
e
eeee
PPPPmP
n
6.3.4. Íåïðåðûâíûå ðàñïðåäåëåíèÿ
6.3.4.1. Ðàâíîìåðíîå ðàñïðåäåëåíèå
Ðàñïðåäåëåíèå âåðîÿòíîñòåé íàçûâàåòñÿ ðàâíîìåðíûì, åñëè
äèôôåðåíöèàëüíàÿ ôóíêöèÿ èìååò ïîñòîÿííîå çíà÷åíèå íà èíòåð-
âàëå, êîòîðîìó ïðèíàäëåæàò âñå âîçìîæíûå çíà÷åíèÿ ñëó÷àéíîé
âåëè÷èíû, ò.å. f (x) = C íà (à; b) è f (x) = 0 ïðè âñåõ îñòàëüíûõ
çíà÷åíèÿõ õ.
Èç óñëîâèÿ
∫
∞
∞−
=
1 )( dxxf
èìååì
∫
=⋅
b
a
dxC
1
èëè Ñ (b a) = 1,
îòñþäà
.
)(
1
ab
C
−
=
316
Òîãäà çàêîí ðàâíîìåðíîãî ðàñïðåäåëåíèÿ çàïèøåì â âèäå:
>
≤<
−
≤
=
.ïðè0
,ïðè
1
,ïðè0
)(
bx
bxa
ab
ax
xf
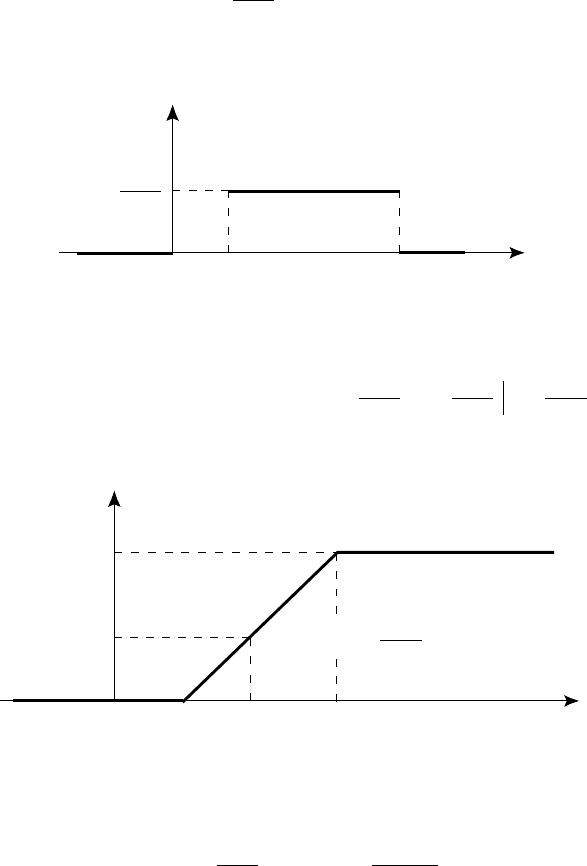
Ãðàôèê ðàâíîìåðíîãî ðàñïðåäåëåíèÿ ïðåäñòàâëåí íà ðèñ. 76.
Íàéäåì èíòåãðàëüíóþ ôóíêöèþ:
.
1
0 )( )(
ab
ax
ab
x
dx
ab
dxCdxdxxfxF
x
a
x
a
x
a
ax
−
−
=
−
=
−
=⋅+⋅==
∫∫∫∫
∞−∞−
Åå ãðàôèê ïðåäñòàâëåí íà ðèñ. 77.
Äëÿ ðàâíîìåðíîãî ðàñïðåäåëåíèÿ:
.
12
)(
)( è
2
)(
2
ab
XD
ab
XM
−
=
+
=
Ðèñ. 77
x
F(x)
0 a x b
>
≤≤
−
−
≤
=
bx
bxa
ab
ax
ax
xF
ïðè1
ïðè
ïðè0
)(
Ðèñ. 76
x
f (x)
0 a b
ab −
1

317
Ïðèìåð 6.26. Ìàñòåð, îñóùåñòâëÿþùèé ðåìîíò íà äîìó, ìî-
æåò ïîÿâèòüñÿ â ëþáîå âðåìÿ ñ 10 äî 18 ÷àñîâ. Êëèåíò, ïðîæäàâ äî
14 ÷àñîâ, îòëó÷èëñÿ íà îäèí ÷àñ. Êàêîâà âåðîÿòíîñòü, ÷òî ìàñòåð
(ïðèõîä åãî îáÿçàòåëåí) íå çàñòàíåò åãî äîìà?
Ðåøåíèå. Èç àíàëèçà ôîðìóëèðîâêè çàäà÷è ïðèíèìàåì ðàâíî-
ìåðíûé çàêîí ðàñïðåäåëåíèÿ ñëó÷àéíîãî âðåìåíè ïðèõîäà ìàñòå-
ðà. Äëÿ îïðåäåëåíèÿ ãðàíèö èíòåðâàëà âðåìåíè ó÷òåì, ÷òî ðàç äî
14 ÷àñîâ ìàñòåð íå ïðèøåë, òî äî 18 ÷àñîâ îí ïðèäåò îáÿçàòåëüíî.
Ñëåäîâàòåëüíî, a = 14 è b = 18, à èíòåãðàëüíàÿ ôóíêöèÿ ðàñïðåäå-
ëåíèÿ:
.
1418
14
)(
−
−
=
−
−
=
x
ab
ax
xF
Òîãäà âåðîÿòíîñòü åãî ïîÿâëåíèÿ â ìîìåíò îòñóòñòâèÿ êëèåí-
òà (ñ 14 äî 15 ÷àñîâ) ðàâíà:
.
4
1
1418
1414
1418
1415
)14( )15( )1514( =
−
−
−
−
−
=−=<< FFXP
6.3.4.2. Ýêñïîíåíöèàëüíîå (ïîêàçàòåëüíîå)
ðàñïðåäåëåíèå
Ïîêàçàòåëüíûì (ýêñïîíåíöèàëüíûì) íàçûâàåòñÿ ðàñïðåäåëå-
íèå âåðîÿòíîñòåé, êîòîðîå îïèñûâàåòñÿ äèôôåðåíöèàëüíîé ôóí-
êöèåé:
≥
<
=
−
,0 ïðè
0 ïðè0
)(
xe
x
xf
x
λ
λ
ãäå
λ
ïîñòîÿííîå ïîëîæèòåëüíîå ÷èñëî.
Íàéäåì èíòåãðàëüíóþ ôóíêöèþ:
,1)(
)(
0 )(
0
0
0
0
0
xx
x
x
x
x
x
x
eee
e
dxedxedxxF
λλ
λ
λλ
λ
λ
λ
λλλ
−−
−
−−
∞−
−=−=
=⋅=⋅=⋅+⋅=
∫∫∫
ãäå
λ
= const.
Âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû íà èíòåðâàëå âðåìåíè îò íóëÿ
äî õ*, ñîîòâåòñòâóþùåé ñîáûòèþ «ïîÿâëåíèå îòêàçà ïîñëå t = õ*»:
.)1(1*)( 1*)( 1*)(
*
tx
eexFxXPxXP
λλ
−−
=−−=−=<<−∞−=>
318
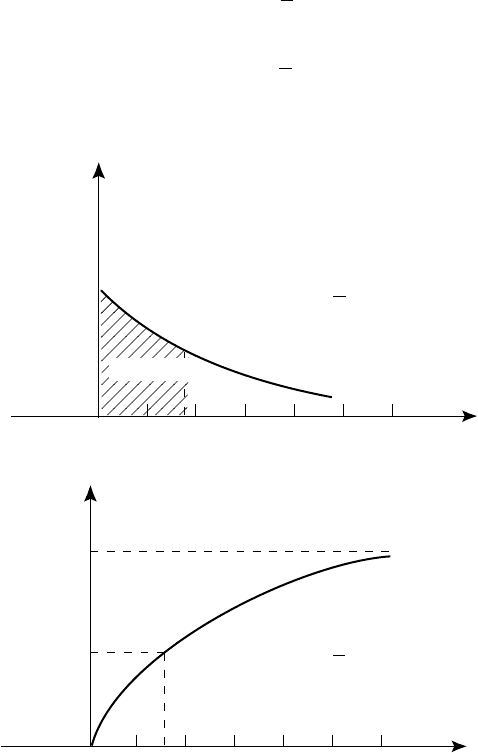
Ïðèìåð 6.27. Ïîñòðîèòü ãðàôèêè èíòåãðàëüíîé è äèôôåðåí-
öèàëüíîé ôóíêöèé ðàñïðåäåëåíèÿ äëÿ ýêñïîíåíöèàëüíîãî çàêîíà
ñ ïàðàìåòðîì
λ
= 0,7, äëÿ êîòîðîãî:
.0 ïðè
2
1
11)(
0ïðè
2
1
0,7
,0ïðè0
0
)(
≥
−≅−=
≥
⋅
<
≈
=
−
−
xexF
x
x
e
xf
x
x
x
x
λ
λ
λ
Ãðàôèêè ýòèõ ôóíêöèé èçîáðàæåíû íà ðèñ. 78.
Ðèñ. 78
0 1 x* 2 3 4 5 6
≥
⋅
<
=
0ïðè
2
1
7,0
0ïðè0
)(
x
x
xf
x
x
f (x)
0,7
S = F(x*)
0ïðè0)(
,0ïðè
2
1
1)(
<=
≥
−=
xxF
xxF
x
1,0
F(x*)
0 1 x* 2 3 4 5 6
x
F(x)

319
Ïðèìåð 6.28. Ðàäèîñèñòåìà, èìåþùàÿ 1000 ýëåìåíòîâ (ñ èí-
òåíñèâíîñòüþ îòêàçîâ
λ
i
= 10
6
îòê / ÷), ïðîøëà èñïûòàíèå è ïðè-
íÿòà çàêàç÷èêîì. Òðåáóåòñÿ îïðåäåëèòü âåðîÿòíîñòü áåçîòêàçíîé
ðàáîòû ñèñòåìû â èíòåðâàëå t
1
< (t = t
1
+ ∆ t) < t
2
, ãäå ∆t = 1000 ÷.
Ðåøåíèå. Èíòåíñèâíîñòü îòêàçà ñèñòåìû èç n = 1000 íåðåçåð-
âèðîâàííûõ ýëåìåíòîâ, êàæäûé èç êîòîðûõ èìååò
λ
i
= 10
6
îòê / ÷,
ðàâíà
λ
s
= n ·
λ
i
= 10
3
îòê / ÷. Ïðè òàêèõ èñõîäíûõ äàííûõ âåðîÿò-
íîñòü îòêàçà ñèñòåìû çà âðåìÿ t = 1000 ÷ ðàâíà:
.37,0)(
1100010
3
====>
−⋅−−
−
eeetXP
t
λ
Ïðèìåð 6.29. Õîëîäèëüíèê èìååò ïîñòîÿííóþ èíòåíñèâíîñòü
îòêàçà ðàâíóþ
λ
= 10
5
îòê / ÷. Êàêîâà âåðîÿòíîñòü, ÷òî îí îòêà-
æåò ïîñëå ãàðàíòèéíîãî ñðîêà
τ
= 20000 ÷àñîâ?
Ðåøåíèå. Ó÷èòûâàÿ ïîñòîÿííóþ èíòåíñèâíîñòü îòêàçîâ, ìîæ-
íî ïðèíÿòü ýêñïîíåíöèàëüíûé çàêîí ðàñïðåäåëåíèÿ âåðîÿòíîñòåé.
Òîãäà âåðîÿòíîñòü îòêàçà â èíòåðâàëå 0 < X < 20000 áóäåò îïðå-
äåëÿòüñÿ ñ ïîìîùüþ èíòåãðàëüíîé ôóíêöèè:
.181,0111)0(
2,02000010
5
≅−=−=−=<<
−⋅−−
−
eeexXP
x
λ
Î÷åâèäíî, ÷òî âåðîÿòíîñòü îòêàçà ïîñëå ãàðàíòèéíîãî ñðîêà
áóäåò ðàâíà P (X > 20000) = 0,819.
Ìàòåìàòè÷åñêîå îæèäàíèå íåïðåðûâíîé ñëó÷àéíîé âåëè÷èíû,
ðàñïðåäåëåííîé ïî ýêñïîíåíöèàëüíîìó çàêîíó, ðàâíî âåëè÷èíå,
îáðàòíîé ïàðàìåòðó ðàñïðåäåëåíèÿ:
,
1
)(
λ
=XM
a äèñïåðñèÿ:
.
1
)(
2
λ
=
XD
Ïðåèìóùåñòâî ýòîãî ðàñïðåäåëåíèÿ â òîì, ÷òî îíî îïðåäåëÿ-
åòñÿ îäíèì ïàðàìåòðîì
λ
, à îáû÷íî ýòè ïàðàìåòðû áûâàþò íåèç-
âåñòíûìè è òðóäíîñòü çàêëþ÷àåòñÿ â òîì, ÷òîáû èõ îöåíèòü.
Ðàññìîòðèì âåðîÿòíîñòü ïîïàäàíèÿ ñëó÷àéíîé âåëè÷èíû Õ â
çàäàííûé èíòåðâàë (à; b):
.)1()1()( )( )(
baab
eeeeaFbFbXàP
λλλλ
−−−−
−=−−−=−=<<
Èòàê,
.)(
ba
eebXàP
λλ
−−
−=<<
320
6.3.4.3. Íîðìàëüíûé çàêîí ðàñïðåäåëåíèÿ
Íà ïðàêòèêå î÷åíü ÷àñòî èìåþò äåëî ñî ñëó÷àéíûìè âåëè÷è-
íàìè, çàâèñÿùèìè îò áîëüøîãî ÷èñëà ñðàâíèòåëüíî íåçíà÷èòåëü-
íûõ è âçàèìíî íåçàâèñèìûõ ôàêòîðîâ.
Ïðèìåð. Ïðè èçìåðåíèè äëèíû ìàòåðèàëà, âåñà ïîðöèè õèìè-
êàòà è ò.ï. èìåþò ìåñòî îøèáêè èçìåðåíèÿ. Íàéòè âåðîÿòíîñòü,
÷òî îøèáêà ëåæèò â ïðåäåëàõ îò ∆x äî +∆õ.
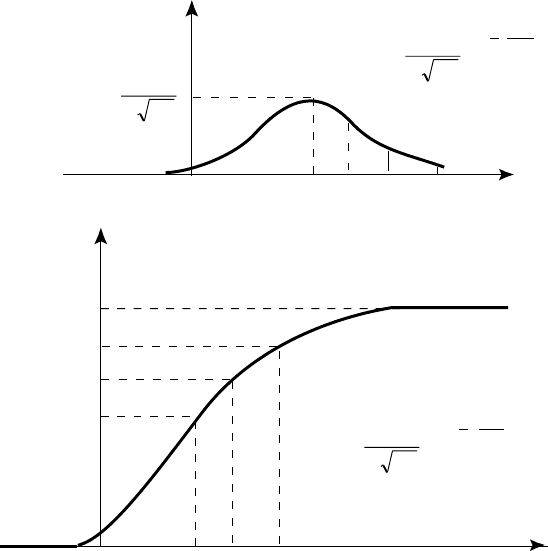
Ïëîòíîñòü ðàñïðåäåëåíèÿ òàêîé ñëó÷àéíîé âåëè÷èíû îïèñûâà-
åòñÿ êðèâîé, ïðåäñòàâëåííîé íà ãðàôèêå (ðèñ. 79), ãäå x
1
= x* ∆x
è x
2
= x* + ∆x. Ýòî íîðìàëüíûé çàêîí ðàñïðåäåëåíèÿ.
πσ
2
1
0 a x
1
x* x
2
x
f(x)
Ðèñ. 79. Ãðàôèê ïëîòíîñòè (êðèâàÿ Ãàóññà)
è èíòåãðàëüíàÿ ôóíêöèÿ íîðìàëüíîãî çàêîíà ðàñïðåäåëåíèÿ
íåïðåðûâíîé ñëó÷àéíîé âåëè÷èíû
dzexF
x
az
∫
∞−
−
⋅−
=
2
2
1
2
1
)(
σ
πσ
1,0
F(x
2
)
F(x
1
)
0,5
0 ax
1
x
2
x
F(x)
2
2
1
2
1
)(
−
−
⋅=
σ
πσ
ax
ex
f
