Sha W., Malinov S. Titanium Alloys: Modelling of Microstructure, Properties and Applications

Подождите немного. Документ загружается.

Neural network models and applications 341

calculation, Thermo-Calc calculation gives more accurate results than ANN

modelling. This might be attributed to the wide validation of the Ti-Data

database during its creation and development phases, using some well-studied

and commonly used phase diagrams, especially binary phase diagrams.

14.1.4 Interaction between alloying elements in

multicomponent systems

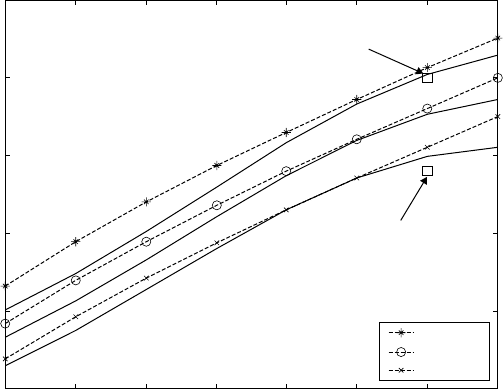
The interaction between aluminium and vanadium in Ti–Al–V system is

evaluated, as shown in Fig. 14.7. In this diagram, the lines with markers are

results calculated using Thermo-Calc (TC), and the continuous lines show

the results calculated by the ANN model. Limited experimental data are

indicated in the diagram with ‘䊐’ markers. The levels of iron and oxygen for

both Thermo-Calc and ANN calculation were set at 0.1 wt.%. The interaction

between molybdenum and aluminium in Ti-xAl-2Sn-4Zr-yMo-0.08Si system

is also evaluated (Fig. 14.8). The results calculated using Thermo-Calc are

plotted in the same figure for comparison, as well as two experimental data

points. From Figs. 14.7 and 14.8, the ANN model probably can give a better

estimation of β

in multicomponent systems compared to Thermo-Calc

calculation. However, such a conclusion should be tested by many more

experimental data in the future.

(°C)

1050

1000

950

900

850

800

750

01 234 56 7

Al (wt.%)

2wt%V

4wt%V

6wt%V

Ti-6.14Al-5.81V-0.07Fe-0.20O

Ti-3.1Al-2.4V-0.06Fe-0.08O

Ti-6.0Al-4.0V-0.1Fe-0.1O

14.7

Interaction between vanadium and aluminium in Ti–Al–V

system.



Titanium alloys: modelling of microstructure342

14.1.5 Linear regression analysis

Linear regression analysis performed on the 200 data-pairs gives the following

expression:

= 882 + 21.1[Al] – 9.5[Mo] + 4.2[Sn] – 6.9[Zr]

– 11.8[V] – 12.1[Cr] – 15.4[Fe] + 23.3[Si] + 123.0[O]

[14.3]

The average of error in calculated β

using this equation is –1 °C, and the

error deviation is 27 °C. Based on the above equation, two parameters [Al]

and [Mo]

can be used to approximately quantify the alloying effects on β

temperature of titanium alloys:

[Al]

= [Al] + 0.2[Sn] + 1.1[Si] + 5.8[O] [14.4]

[Mo]

= [Mo] + 1.2[V] + 0.7[Zr] + 1.3[Cr] + 1.6[Fe]

[14.5]

The β

temperature can therefore be calculated using the following expression.

= 882 + 21.1[Al]

– 9.5[Mo]

[14.6]

(°C)

1050

1000

950

900

850

800

01234567

Al (wt.%)

2wt%Mo

4wt%Mo

6wt%Mo

Ti-6Al-2Sn-4Zr-6Mo-0.15Fe-0.15O

Ti-6Al-2Sn-4Zr-2Mo-0.08Si-0.25Fe-0.15O

14.8

Interaction between molybdenum and aluminium in Ti-

Al-2Sn-

4Zr-

Mo-0.08Si system.



Neural network models and applications 343

14.1.6 Summary

Artificial neural network modelling and thermodynamic calculation can

accurately predict the β-transus temperature of titanium alloys when the

alloy chemistry is known. The influences of the alloying elements aluminium,

molybdenum, vanadium and oxygen on the β-transus temperature in binary

systems can be quantitatively revealed. Thermo-Calc calculation gives a

better estimation of the β-transus than the ANN model. The interactions

among alloying elements V–Al, and Mo–Al are evaluated. Probably, the

ANN model could give a better estimation of the β-transus than Thermo-

Calc, in multicomponent systems. In addition, linear regression analysis can

be used to quantify the alloying effects on β-transus.

14.2 Time–temperature–transformation diagrams

It is very important to know the kinetics of phase transformations taking

place under different heat treatment regimes. The kinetics are described by

time–temperature–transformation (TTT) and continuous-cooling–

transformation (CCT) diagrams. The knowledge of these diagrams for different

alloys would allow the optimisation of the processing parameters (temperature,

time, cooling/heating rates) in order to achieve desirable microstructures.

The idea of computer modelling and prediction of these diagrams is very

attractive. There is limited work on physical modelling of TTT diagrams for

Ti-alloys based on the Johnson–Mehl–Avrami theory. These models, however,

concern a very limited number of alloy types, and they do not predict what

would happen if the composition is changed.

This section will demonstrate an artificial neural network model for the

prediction of TTT diagrams of titanium alloys as a function of their composition.

It also aims to better explain the influence of different alloying elements

over the transformation kinetics.

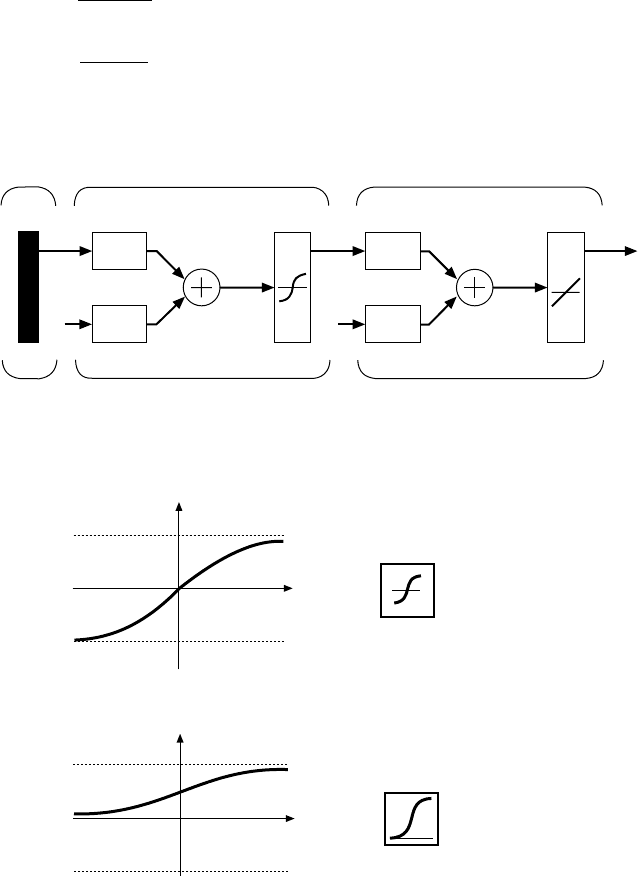
14.2.1 Model description

A general scheme of the designed NN is given in Fig. 13.1a.

Database, analysis and pre-processing

For reliable training and performance of any NN, we need an appropriate

database. The data set is constructed by collecting available TTT diagrams

for titanium alloys. The full list of the literature sources for these is given by

Malinov et al. (2000). In total, 189 TTT diagrams for different Ti alloys are

used fully or partly in the database. About 35% of the diagrams are for

binary Ti–X alloys and the remainder concern ternary or more complex



Titanium alloys: modelling of microstructure344

systems. Most of the diagrams are for commercial titanium alloys. The input

parameters of the NN are the chemical compositions of the alloys. Nine

inputs are chosen – the eight most frequently used alloying elements (Al,

Mo, Sn, Zr, Cr, Fe, V, Cu) and oxygen (see Fig. 13.1a). Some alloys also

contain Nb, Co and Ni. However, since the number of the alloys containing

these elements is small, either these alloys are excluded from the data set or

the extra elements are converted to their molybdenum equivalent. The inputs

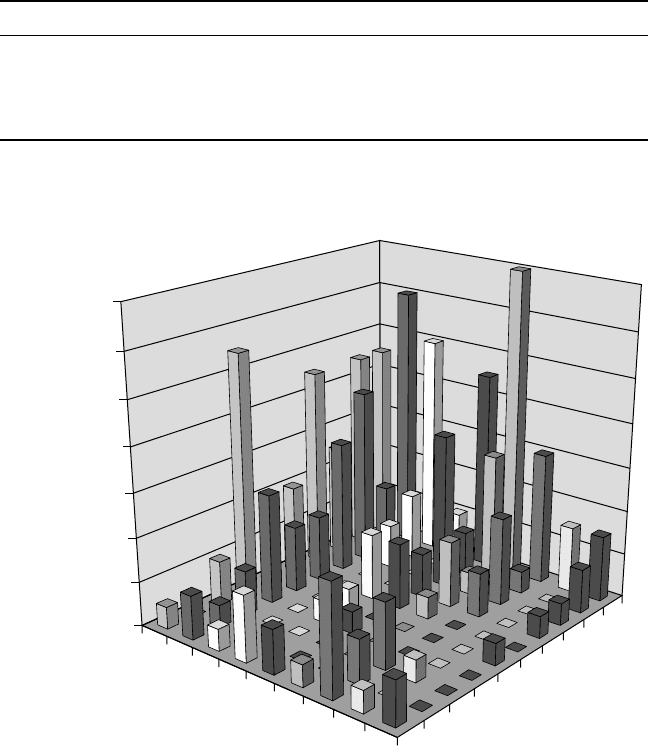
are listed in Table 14.3, and the distribution of their values is presented in

Fig. 14.9.

Table 14.3

Statistical analysis of the input variables for the TTT model

Alloying element Al Mo Sn Zr Cr Fe V Cu O

Number of alloys

containing this

element 52 46 17 11 27 27 24 6 11*

Range (wt.%) 0–8.0 0–15.7 0–11.0 0–6.4 0–11.0 0–5.2 0–16.0 0–8.0 0.1–0.55

*This is the number of alloys containing more than 0.1 wt.% O; this was adopted

as the minimum and inevitable oxygen level. When the oxygen level of any alloy

was unknown, it was taken as 0.1wt.%.

Number

Alloying element

Interval

14.9

Distribution of the input data set for TTT neural network model.



Neural network models and applications 345

Typically, neural networks work with numerical formats of both input and

output data. Therefore the output parameter, which in this particular case is

a graph, has to be presented in a numerical format. Thus, all diagrams are

scanned, put in electronic format and rescaled in one same scale.

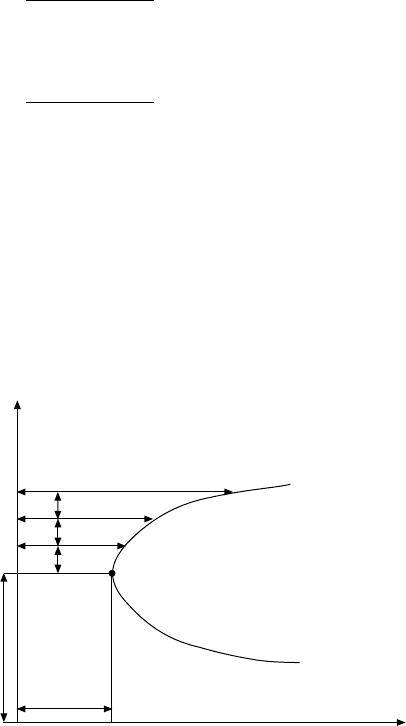
Figure 14.10 shows the approach used here for digitising and presenting

a diagram as a set of numbers. The nose point (n in Fig. 14.10) is used as a

base point. This point is specified with its two coordinates – temperature (T

)

and time (τ

). Thereafter, the entire curve is described by a set of numbers

giving the relative increase of the time when the temperature is increased or

decreased by ∆T. These values are computed using:

time( + )

time( )

∆

[14.7]

for the upper part of the curve and:

time( – )

time( )

∆

[14.8]

for the lower part of the curve, where: rt

, is relative time; time (T)

, is time

corresponding to temperature T; time (T + ∆T)

, time (T – ∆T)

, are times

corresponding to temperature T + ∆T and T – ∆T, respectively.

The martensite start temperature (M

) is also included as an output to

complete the TTT diagrams. In this way, 23 outputs are introduced, namely:

time and temperature of the nose point (T

and τ

), ten numbers describing

the upper part of the curve, ten numbers describing the lower part of the

curve, and martensite start temperature (M

Temperature

∆

Time

14.10

Digitisation of TTT diagrams.



Titanium alloys: modelling of microstructure346

The following remarks are necessary:

• The data for M

temperature are mainly from binary systems. Only 30

data pairs for more complicated systems are used.

• In some cases, there is a contradiction between the TTT diagrams for the

same alloy taken from different sources and authors.

• All diagrams used are for alloys after solution treatment in the

homogeneous β-field (50–100 °C above β-transus for 20–30 min). No

alloy had solution heat treatment within the α + β field.

• All TTT diagrams used concern the kinetics of the monovariant β to

α + β transformation.

• TTT diagrams for decomposition of martensite during reheating (ageing)

are not included.

• TTT diagrams describing the invariant decomposition of β through

eutectoid or peritectoid transformation are not included.

• Only data for the start of the transformation are treated.

Training

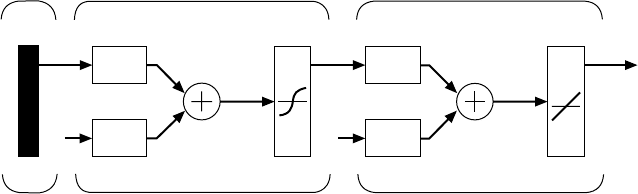
The general model of the created NN (Fig. 13.1a) consists of separate networks

for:

(1) the temperature and the time of the nose point (T

and τ

);

(2) description of the curve; and

(3) M

temperature.

In Fig. 14.11, an example of the neural network for the prediction of the nose

point is given. Figure 14.12 shows the architecture of the neural network for

the prediction of the curve above and below the nose point (τ

, τ

, etc., in

Fig. 14.10).

Input Hidden layer Output layer

= tansig (IW

1,1

+ b

) a

= purelin (LW

2,1

+ b

)

9 × 1

1,1

9 × 9

9 × 1

2,1

2 × 9

2 × 1

14.11

Architecture of the neural network for TTT diagram nose point

simulation.



Neural network models and applications 347

Different numbers of neurons in the layers were applied for different

networks (Fig. 14.12). Before the training of the network, both input and

output variables were normalised within the range from –1 to 1 using Eq.

[13.1b].

In the hidden layer, tan-sigmoid transfer function

f(x

) =

1 +

– 1, Fig. 14.13

–2













and log-sigmoid transfer function

f(x

) =

1 +

, Fig. 14.14

–













were attempted. When the logsig was applied,

the inputs and the outputs were normalised within the range 0–1 using

Input Hidden layer Output layer

= tansig (IW

1,1

+ b

) a

= purelin (LW

2,1

+ b

)

9 × 1

18 × 1

1,1

18 × 9

18 × 1

2,1

10 × 18

10 × 1

14.12

Architecture of the neural network for upper and lower part of

the TTT diagram simulation.

–1

14.13

Tan-sigmoid transfer function used in the hidden layer.

14.14

Log-sigmoid transfer function used in the hidden layer.



Titanium alloys: modelling of microstructure348

Eq. [13.1a]. The networks were automatically initialised with the default

parameters. The Levenberg–Marquardt algorithm was used. The learning

rate was 0.01 and the epoch (the number of training cycles) was 1000.

When the training was performed against a validation set, the groups were

as follows: one half, training set; one quarter, validation set; and one quarter,

test set. By varying all the parameters described above, trained NNs with the

best performance (Fig. 14.15) were achieved.

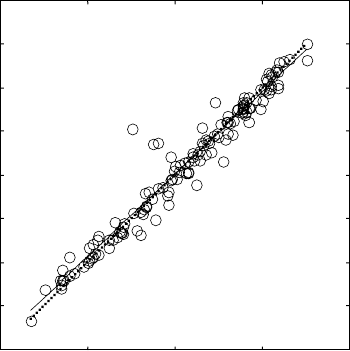
Figure 14.15 shows an analysis of the network response, using the linear

regression between the network output and the corresponding targets. For all

trained NNs, the outputs track the targets very well. The main source of

deviation is the above mentioned contradiction in the experimental data.

Similar performance is achieved for the other NNs used for the simulation of

the curve description and the M

. R-values for all cases of training, validation

and test data sets are above 0.92. This means that a good performance of the

NN has been achieved, and the network can be used for further simulation.

14.2.2 Calculation results and comparison with

experiments

On the basis of the trained neural networks, the model for the simulation of

TTT diagrams for titanium alloys has been created. This model can be used

to predict diagrams with sufficient accuracy within the range of the used data

set (see Table 14.3 and Fig. 14.9). In the following, some TTT diagrams for

different Ti alloys are predicted by this model and are thereafter analysed by

seeking some explanation of the results from the metallurgical point of view

(see Figs. 14.16–14.18).

The influence of aluminium (Fig. 14.16a) and vanadium (Fig. 14.16b) on

the decomposition of the β phase for one of the most popular titanium

systems (Ti–Al–V) is modelled. TTT diagrams are computed assuming

increased and decreased content of aluminium or vanadium from Ti-6Al-4V.

With the increasing of the aluminium content, the C-curve, indicating the

start of the β to α + β transformation, is shifted to higher temperatures and

shorter times (see Fig. 14.16a). The influence of vanadium is the opposite;

increasing the vanadium content shifts the C-curve to lower temperatures

and longer times (see Fig. 14.16b). The predicted dependence of the temperature

is in accordance with the well established influence of the above elements

over β-transus temperature. From the metallurgical point of view, it is also

not surprising that, in general, the incubation period is shorter when the

transformation takes place at higher temperatures because of the higher

diffusivity. The results are therefore consistent with what is expected from

the theory of phase transformations.

The influence of vanadium on the martensite start temperature shows a

similar tendency. With increasing vanadium content, M

is decreased (Fig.



Neural network models and applications 349

Data points

A = T

Best linear fit

NN calculation (

)

1000

900

800

700

600

500

400

300

200

200 400 600 800 1000

Experimental (

)

(a)

R = 0.979

Best linear fit: A = (0.95) T + (32)

14.15

Performance of the neural network model of the nose point

temperature, in °C, of TTT diagrams on: (a) training, (b) testing, and

NN calculation (

)

900

800

700

600

500

400

300

300 400 500 600 700 800 900

Experimental (

)

(b)

R = 0.974

Best linear fit: A = (0.937) T + (40.2)



Titanium alloys: modelling of microstructure350

14.16b). The modelled aluminium influence on M

seems to be more

complicated. Such a character of the aluminium influence has been inducted

into the model from the data set.

For Ti-6Al-4V alloy, the influence of the interstitial oxygen is also modelled

(Fig. 14.17). Attention is paid to oxygen, as the level of impurities, especially

oxygen, has a high influence on the behaviour of titanium and its alloys.

There is a very large influence of oxygen on the transformation kinetics.

A very small increase of the oxygen content causes a significant shift of the

curve to higher temperatures and shorter times (see Fig. 14.17). Hence,

oxygen acts in the same direction as aluminium, but much more strongly.

Such influence of oxygen over TTT diagrams (especially start curves) of

titanium alloys was reported for Ti-Mo and VT15, on the basis of experimental

studies. The predicted TTT diagrams for Ti-6Al-4V match well with the

experimental one (Fig. 14.17).

The predicted martensite start temperature is not affected so much when

the oxygen content varies in the range from 0.05 to 0.2 wt.%. When the

oxygen content is increased beyond 0.2 wt.%, M

increases.

Although the calculated oxygen influence on the TTT diagram of Ti-6Al-

4V is reasonable, in the data set, only 11 alloys contain oxygen. This means

that the oxygen influence has been simulated on the basis of the participation

of only those alloys in the training process of the model. Therefore, the

modelling of the oxygen content should be performed with caution, and

large deviations are possible when the model is applied.

NN calculation (

)

1000

900

800

700

600

500

400

300

200

200 400 600 800 1000

Experimental (

)

(c)

R = 0.978

Best linear fit: A = (0.946) I + (34.1)

14.15

Contined

