Sha W., Malinov S. Titanium Alloys: Modelling of Microstructure, Properties and Applications

Подождите немного. Документ загружается.

Neural network models and applications 361

The neural network has been used to study the influence of different alloying

elements on transformation kinetics in titanium alloys. It has been shown

that:

• aluminium shifts the C-curve to higher temperatures and shorter times;

• vanadium shifts the C-curve to lower temperatures and longer times;

• molybdenum has a dual influence on the transformation kinetics;

• small increases in the oxygen level induce significant shifts of the C-

curve to higher temperatures and shorter times.

Using the model, TTT diagrams for a number of commercial titanium alloys

have been predicted. The predictions of the model are consistent with what

might be expected from a knowledge of titanium alloys and phase

transformation theory.

A graphical user interface for use of the model has been created. The

program and the model can be used for:

• simulation of TTT diagrams for titanium alloys as a function of chemical

composition;

• investigation of the influence of different alloying elements on the β to

α transformation kinetics in titanium alloys;

• optimisation of the chemical composition;

• significant reduction of the experimental work for measurement of TTT

diagrams for titanium alloys.

In the chapter, we have stressed the consistence between neural network

predictions and a knowledge for the phase transformations in titanium alloys,

especially in sections 14.2.2 and 14.2.3.

14.3 An example of MatLab program code

for neural network training

The following example is for one particular combination of NN parameters,

including training algorithm, transfer function and NN architecture (number

of neurons in the hidden layer). During the development of the models, these

parameters were changed in order to find the best combination of training

algorithm, transfer function and NN architecture.

%This program is a part of NN for prediction of %properties

in Ti alloys

%Rm

%Training

%the following reads data file and put it into matrix M

load tb_Rm.txt;



Titanium alloys: modelling of microstructure362

M = tb_Rm;

%Dimensions

sz = size(M);

rws = sz(1);

cls = sz(2);

%Generates random

rnd1 = rand(rws);

rnd = rnd1(:,1);

M_r = M;

M_r(:,16) = rnd;

M_r = sortrows(M_r,16);

M = M_r(:,1:15);

%The next divide the data into train and test groups

M_all = M(1:rws,:);

M_tr = M(1:471,:);

M_val = M(471:rws,:);

%inputs

PP_all = M_all(:,2:14);

PP_tr = M_tr(:,2:14);

PP_val = M_val(:,2:14);

%outputs

TT_all = M_all(:,15);

TT_tr = M_tr(:,15);

TT_val = M_val(:,15);

p_all = PP_all’;

p_tr = PP_tr’;

p_val = PP_val’;

t_all = TT_all’;

t_tr = TT_tr’;

t_val = TT_val’;

%normalization

[pn_tr,minp_Rm,maxp_Rm,tn_tr,mint_Rm,maxt_Rm] =

premnmx(p_tr,t_tr);



Neural network models and applications 363

%min and max of the input

PR = [min(pn_tr’); max(pn_tr’)]’;

%creating a network

net_Rm=newff(PR, [13,1], {‘tansig’, ’purelin’}, ’trainbr’);

%training parameters

net_Rm.trainParam.show = 5;

net_Rm.trainParam.lr = 0.01;

net_Rm.trainParam.epochs = 250;

net_Rm.trainParam.goal = 0.00000001;

%training

net_Rm=train(net_Rm,pn_tr,tn_tr);

%post training analyses

an = sim(net_Rm,pn_tr);

a = postmnmx(an,mint_Rm,maxt_Rm);

figure(1)

[m(1),b(1),r(1)] = postreg(a(1,:),t_tr(1,:));

p_val_n = tramnmx(p_val,minp_Rm,maxp_Rm);

a_val_n = sim(net_Rm,p_val_n);

a_val = postmnmx(a_val_n,mint_Rm,maxt_Rm);

figure(2)

[m(2),b(2),r(2)] = postreg(a_val(1,:),t_val(1,:));

p_all_n = tramnmx(p_all,minp_Rm,maxp_Rm);

a_all_n = sim(net_Rm,p_all_n);

a_all = postmnmx(a_all_n,mint_Rm,maxt_Rm);

figure(3)

[m(3),b(3),r(3)] = postreg(a_all(1,:),t_all(1,:));

%save(’tr_Rm1’,’net_Rm’,’minp_Rm’,’maxp_Rm’,’mint_Rm’,’maxt_Rm’)

14.4 References

Cristianini N and Shawe-Taylor J (2000), An Introduction to Support Vector Machines

and Other Kernel-based Learning Methods, Cambridge: Cambridge University Press.



Titanium alloys: modelling of microstructure364

Guo Z and Sha W (2000), ‘Modelling of beta transus temperature in titanium alloys using

thermodynamic calculation and neural networks’, in: Gorynin I V and Ushkov S S

(eds), Titanium’99: Science and Technology, Proceedings of the Ninth World Conference

on Titanium, St. Petersburg, Russia: Central Research Institute of Structural Materials,

61–68.

Guo Z and Sha W (2004), ‘Modelling the correlation between processing parameters and

properties of maraging steels using artificial neural network’, Comput Mater Sci, 29

(1), 12–28.

Hu Y H and Hwang J N (eds) (2001), Handbook of Neural Network Signal Processing,

Boca Raton, FL: CRC Press.

Malinov S, Sha W and Guo Z (2000), ‘Application of artificial neural network for prediction

of time–temperature–transformation diagrams in titanium alloys’, Mater Sci Eng A,

283A (1–2), 1–10.



365

Neural network models and applications

in property studies

Abstract: A model is described in detail for the prediction of properties of

titanium alloys at different temperatures as functions of processing

parameters and heat treatment cycles. The chapter also discusses how to use

the model for the optimisation of processing and heat treatment parameters.

It continues with introducing a separate model, developed for prediction of

fatigue stress life S-N diagrams for Ti-6Al-4V alloy under various

conditions, again using an artificial neural network. The third part of the

chapter shows a model for the prediction of the correlation between alloy

composition and microstructure and tensile properties in γ-based titanium

aluminide alloys using ANN.

Key words: neural network, mechanical properties, fatigue, microstructure-

property correlations, tensile properties.

15.1 Correlation between processing parameters

and mechanical properties

We will present a systematic account of the artificial neural network models

for the analysis and the prediction of the mechanical properties of titanium

alloys as functions of the processing (heat treatment) parameters and alloy

composition. The work is motivated by the desire to create a tool for

optimisation of the processing parameters and the alloy composition.

15.1.1 Model description

A most general scheme of the model is given in Fig. 13.1b. The input parameters

of the neural network are alloy composition, heat treatment parameters and

work (test) temperature. The composition includes the most commonly used

alloying elements in titanium alloys, namely Al, Mo, Sn, Zr, V, Cr, Fe, Cu,

Bi, Si, Nb, Ta, Mn, and O. Typical heat treatments of titanium alloys are

taken into account: (i) annealing in α, α + β and β regions; (ii) solution

treatment in β and α + β regions followed by ageing at different temperatures;

(iii) duplex annealing. Since the titanium alloys are considered as desirable

and sometimes essential for many structural applications at high temperatures,

the test/work temperature is included as an input in the model. In this way,

the model is extended to trace the correlation ‘processing parameters – working

conditions (temperature) – mechanical properties’.

The outputs of the neural network model are the nine most important

mechanical properties, namely ultimate tensile strength, tensile yield strength,



Titanium alloys: modelling of microstructure366

elongation, reduction of area, impact strength, hardness, modulus of elasticity,

fatigue strength and fracture toughness.

Data set and input/output parameters

The database was constructed by collecting available data on mechanical

properties for titanium alloys with different heat treatment conditions and

working temperatures. In total, 764 input/output data pairs were collected

(see Appendix at the end of this chapter for list of the alloys used).

The selection of the input parameters is a very important aspect of neural

network modelling. Before training, the number of input parameters should

be restricted by ignoring the dependent input parameters. In this model the

following were used as input parameters.

Alloy composition

After pre-processing analysis, the 14 alloying elements initially chosen (see

above) were reduced to 11, namely Al, Mo, Sn, Zr, Cr, Fe, V, Si, Nb, Mn and

O. Cu, Bi and Ta were each contained in only one alloy, Ti-2.5Cu (IMI 230),

Ti-6Al-2Sn-1.5Zr-1Mo-0.35Bi-0.1Si and Ti-6Al-2Nb-1Ta-0.8Mo, respectively,

at different conditions and temperatures. The data pairs containing Cu and Bi

were excluded from the training database, while Ta, where present, was

converted to Nb equivalent. When the oxygen level of the alloy was unknown,

an amount of 0.15 wt.% was attributed. Modelling of the oxygen influence

on the mechanical properties was based on 61 data pairs with oxygen content

above 0.2 wt.% or below 0.1 wt.% (ELI alloys). For the remaining part of the

database, the oxygen content was in the range 0.1–0.2 wt.%. When iron was

not an alloying element in the titanium alloy, an amount of 0.15 wt.% was

attributed. Analysis of the database in terms of the alloy elements present is

given in Table 15.1.

Heat treatment

Nine classical heat treatment types for titanium alloys for which data in the

literature exist were taken into account in the neural network model. Since

neural networks operate with digits, the heat treatments are digitised by

means of attributing different digits to the different heat treatments. The

distribution of the heat treatments is presented in Table 15.2, showing the

number of data pairs corresponding to each type of heat treatment. Large

amounts of data are available for the two most popular heat treatments of

titanium alloys, namely annealing in the α + β field and solution treatment

in the α + β field followed by ageing.



Neural network models and applications in property studies 367

Table 15.1

Analysis of the chemical composition (concentration in wt. %) of the alloys used for training and test

Element Al Mo Sn Zr Cr Fe V Cu

(a)(d)

(b)(d)

Si Nb Ta

(c)(e)

Mn O

Number of data 699 467 247 275 163 175

(f)

272 3 7 150 105 39 21 61

(g)

pairs containing

this element

Minimum 0 0 0 0 0 0.15 0 2.5 0.35 0 0 1 0 0.05

Maximum 8 15 11 11 11 5 16 2.5 0.35 0.5 7 1 8 0.33

Mean 4.91 4.89 3.38 4.73 4.78 1.36 6.49 2.5 0.35 0.20 1.98 1 4.90 0.16

Standard deviation 1.69 4.70 2.08 2.78 3.63 0.92 4.32 0.0 0.00 0.11 0.89 0 3.33 0.09

(a) Only in one alloy (Ti-2.5Cu (IMI 230));

(b) Only in one alloy (Ti-6Al-2Sn-1.5Zr-1Mo-0.35Bi-0.1Si);

(d) Excluded from the data set;

(e) Converted to niobium;

(f) Number of data pairs containing iron as an alloying element;

(g) Number of data pairs containing oxygen different from the usual.



Titanium alloys: modelling of microstructure368

Temperature

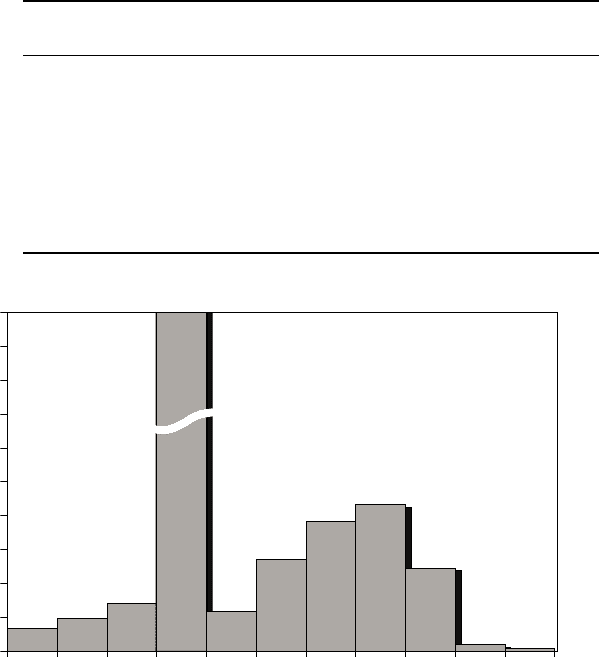
Most of the data on the different mechanical properties are at room temperature

(see Fig. 15.1). However, there are many data at –193, –70, –62, 20, 100,

200, 300, 316, 350, 400, 427, 450, 480, 500, 538, 550 and 600 °C. Some data

for mechanical properties at very low (–253 °C) as well as at very high (800

°C) temperatures were collected. The analysis of the database distribution is

presented in Fig. 15.1, in a form of a histogram showing the number of data

pairs in each temperature interval. This analysis shows that the model can

work with sufficient accuracy within the temperature interval of –100 to

+600 °C.

Table 15.2

Heat treatments used in the database and their digitising

Heat treatment Number of Digitising

data pairs

Without heat treatment 16 0

Annealing (β)451

Annealing (α+β) 237 2

Annealing (α)293

Solution treatment (β)184

Solution treatment (α+β)135

Solution treatment (β) and ageing 29 6 + (1-

age

transus

)

Solution treatment (α+β) and ageing 247 7 + (1-

age

transus

)

Duplex annealing 130 8

Number of data pairs

200

180

160

140

120

100

–250 –150 –50 50 150 250 350 450 550 650 750

(°C)

408

15.1

Distribution in the database of mechanical properties of titanium

alloys versus test/working temperature.



Neural network models and applications in property studies 369

Different numbers of data pairs for the different mechanical properties

were collected (Table 15.3). Most of the data are for tensile test properties,

but there is also a sufficient amount of data for the other mechanical properties.

The ranges of variation of the properties, as well as the conditions at which

data with respect to the alloy composition, heat treatment and temperature

exist, are shown in Table 15.3.

Neural network training

The choice of transfer function is one of the decisions which must be made

by the user, although it is not usually a very critical factor. In their infancy,

neural networks were trained using a method known as backpropagation.

The method suffers from the drawback that the adjustments which reduce

the errors (improvement of error) on a given set of data, may increase the

errors on the other sets of data, so the process is constantly undoing the

improvements made so far.

A much better approach has turned out to be to use one of the many

methods of numerical optimisation which have been developed for solving

nonlinear sums-of-squares problems. The nonlinearity arises because the

relationships between outputs and weights of an artificial neural network are

nonlinear, although well defined. It is this nonlinearity which makes it necessary

to use iterative methods. The most efficient method in most cases is the

Gauss–Newton algorithm, but this method can suffer from numerical instability

unless the initial estimate of the weights is fairly accurate, so it is unreliable.

On the other hand, the method of steepest descent is reliable, but highly

inefficient. In fact, backpropagation becomes equivalent to steepest descent

when adjustments are made, not for each error separately, but to all at once

– so-called batch-backpropagation. The method used in this book is the

Levenberg–Marquardt algorithm, which can be regarded as a compromise

between Gauss–Newton and steepest descent, heavily favouring the former.

Typically, the use of Levenberg–Marquardt leads to a reduction of orders of

magnitude in the number of training iterations required compared with

backpropagation, and is highly reliable.

The general model of the neural network (Fig. 13.1b) consists of separate

neural network models for each output mechanical property. In the general case,

these models include 13 neurons in the input layer, 13 neurons in the hidden layer

and 1 neuron in the output layer. The most accurate predictions of the neural

networks are obtained with the hyperbolic tangent sigmoid transfer function.

Neural network test and performance

The predicted values from the trained neural network outputs track the targets

very well (see the performance example shown in Fig. 15.2). Acceptable



Titanium alloys: modelling of microstructure370

Table 15.3

Analysis of the output data for training and test of neural network for prediction of the mechanical properties of titanium

alloys

Output Number Min. Max. Mean Standard Temperature

of data deviation range (°C)

Tensile strength (MPa) 707 151 2250 975 282.65 –253 to 800

0.2% yield strength (MPa) 662 97 2050 859 282.89 –253 to 800

Elongation (%) 581 1 50 13 6.51 –253 to 800

Reduction of area (%) 421 4 92 38 17.80 –196 to 800

Charpy impact strength (J) 124 8 119 33 21.62 –196 to 500

Rockwell hardness (HRC) 98 24 57 36 5.56 –253 to 300

Modulus of elasticity (GPa) 259 57 140 105 13.37 –253 to 800

–1

fatigue strength (MPa)* 74 220 900 537 140.07 20 to 600

fracture toughness (MPa-m

1/2

)** 69 24 176 78 34.44 –253 to 316

*No data for solution treatment (β).

**No data for manganese.

