Seuront L. Fractals and Multifractals in Ecology and Aquatic Science

Подождите немного. Документ загружается.

254 Fractals and Multifractals in Ecology and Aquatic Science

also be found in energy resources (Asmus 2003; Anderson and Leach 2004). In the eld of dynami-

cal systems, intermittency has been related to several types of transitions to chaos and classied as

types I, II, and III intermittency when the system under consideration is in proximity to the saddle

node, Hopf, and reverse period doubling bifurcation (Pomeau and Manneville 1980). By analogy to

the bifurcation diagrams detailed in Section 6.1.1 (Figure 6.3 and Figure 6.4), in these three types

of intermittency, the temporal evolution of a system can be divided into ranges of the time in which

the behavior of the system is almost periodic (that is, laminar phases) and exhibits chaotic bursts.

Chaos-chaos intermittency is due to crisis phenomena occurring in the system (Ott 1993, 2002)

and the on-off intermittency is due to a symmetry breaking bifurcation (Pikovsky 1984; Platt et al.

1993). Practically, the identication of the type of the intermittency observed may yield important

information about a system by dening the bifurcations possible for its dynamics (see, for example,

ebrowski and Baranowski 2004; Alvarez-Llamoza et al. 2008).

The phenomenon of intermittency has widely been mixed up with its statistical consequences,

and thus generally poorly dened even in specialized monographs. The literature, hence, recur-

rently refers to intermittency through statements such as “the kurtosis is a useful measure of inter-

mittency for signals having a bursty aspect” (Frisch 1996), “the signals tended to become bursty

when the order of differentiation is increased” (Frisch 1996), “most of the time the gradients would

still be of the order of magnitude of their standard deviation, but occasionally we should expect

stronger bursts, more often than in the Gaussian case” (Jiménez 1997), “the discrepancies between

the Kolmogorov predictions and the experimental values of the high-order moments” (Pope 2000),

and “we occasionally should expect stronger bursts than expected in a non-intermittent, homoge-

neous turbulence, which accentuate the skewness of a given probability distribution, causing it to

deviate from Gaussianity” (Seuront et al. 2001).

The production of turbulence is not a continuous process but usually has an intermittent

character and the turbulence appears as bursts (Svendsen 1997). This intermittency has been

acknowledged as “a common phenomenon in many complex systems, and a natural consequence

of cascades” (Jiménez 2000). Intermittency has also been related to the coherent nature of turbu-

lence and the presence of strong vortices, with diameters on the order of 10 times the Kolmogorov

length scale l

, l

= (n

/e)

1/4

where n is the kinematic viscosity (m

−1

) and e the turbulent kinetic

energy dissipation rate (m

−3

) (Siggia 1981; Jiménez et al. 1993; Jiménez and Wray 1994). The

term intermittency has alternatively been coined to describe “the phenomena connected with

the local variability of the dissipation” (Jiménez 1998) as well as “instantaneous gradients of

scalars such as temperature, salinity or nutrients, greatest at scales similar to the Kolmogorov

microscale” (Gargett 1997).

Pope (2000), and more recently Jiménez (2006) in the Encyclopedia of Mathematical Physics,

distinguished external from internal intermittencies. External intermittency refers to the coex-

istence of turbulent and laminar regions in inhomogeneous turbulent ows, such as in bound-

ary layers or in free-shear layers. The interface between laminar irrotational ow and turbulent

vortical uid is typically sharp and corrugated (Jiménez 2006). As a consequence, an observer

sitting near the edge of the layer is immersed in turbulent uid only part of the time and hence

experiences an intermittently turbulent ow. In this context, an intermittent ow is characterized

by a uid motion that is “sometimes laminar and sometimes turbulent” (Pope 2000). For the engi-

neering community in uid mechanics, intermittency is also viewed as a transition between lami-

nar and turbulent ows. Specically, Wilcox (1998) considers that “approaching the freestream

from within the boundary layer, the ow is not always turbulent. Rather, it is sometimes laminar

and sometimes turbulent, that is, it is intermittent.” Internal intermittency (Pope 2000; Jiménez

2006) is specically related to the increasingly non-Gaussian properties of velocity uctuations

as spatial separation increases. This property is responsible for the long tails of the probability

distributions of the velocity derivatives.

A more intuitive denition that can directly be applied in ecology stated that “this form of vari-

ability reects heterogeneous distributions with a few dense patches and a wide range of low density

2782.indb 254 9/11/09 12:15:00 PM

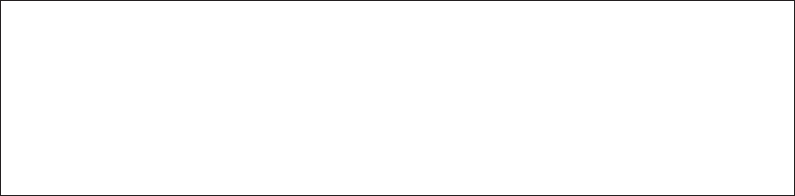
From Fractals to Multifractals 255

patches” (Seuront et al. 2001). Most of the previously published work referred to intermittency in

the framework of turbulent ows, including wave turbulence (Biven et al. 2001; Newell et al. 2001;

Bouruet-Aubertot et al. 2004), plasma turbulence (Sorriso-Valvo et al. 2001; Hidalgo et al. 2006),

and solar wind turbulence (Bruno et al. 2001; Chapman et al. 2005). However, a general consensus

can be reached considering that a given pattern or process is intermittent in space or in time if (1) it

is characterized by sharp local uctuations, (2) it is responsible for a skewed probability distribution,

and (3) it has a long-term memory signature, perceptible from the power-law form of its autocor-

relation function.

8.1.4 va r i a b i l i T y , in h o m o g E n E i T y, a n d hE T E r o g E n E i T y : TE r m i n o l o g i c a l co n s i d E r a T i o n s

In ecology, the term variability refers to changes in the values of a given quantitative or qualita-

tive descriptor; it is distinct from heterogeneity, which refers to a composition of different entities

or kinds of elements (Kolasa and Rollo 1991; Merriam-Webster’s Collegiate Dictionary 2008).

This distinction is, however, not as clear as may appear at rst glance, with meanings essentially

dependent on the choice of approach (Naeem and Colwell 1991; Shashack and Brand 1991). Even

papers devoted to the synthesis of these concepts (Kolasa and Rollo 1991; Naeem and Colwell 1991;

Shashack and Brand 1991) may be misleading in that spatial and temporal heterogeneity are used

to describe spatial or temporal variability, respectively, irrespective of the basic previous deni-

tions. Denitions themselves appear to be highly variable even within a collective synthetic work

on the subject (Levin et al. 1993). Spatial heterogeneity was then dened as an equivalent of spatial

autocorrelation (van Hes 1993), despite the stress for a clear distinction between these two concepts

(Davis 1993). Fractal geometry and the resulting scaling properties have also been suggested as a

way to characterize space-time heterogeneity in ecology (Milne 1991). In aquatic sciences, both

physical and biological patterns and processes have been referred to in terms of “temporal intermit-

tency” and “spatial heterogeneity”’ (Platt et al. 1989).

Terminological ambiguities are potentially detrimental to scientic progress (Popper 2002) and

are not limited to ecological sciences (Box 8.1). The term inhomogeneity, seldom used in the lit-

erature, but as a synonym of variability, nonhomogeneity, or nonuniformity (Coplen and Krouse

1998; Blundell and Rawlings 1999; Jiménez 2006), is suggested hereafter as a way to describe the

variability of a descriptor structured in space or in time in terms of scaling, and discussed as a

way to reach a terminological consensus. A descriptor exhibiting nonscaling properties cannot be

distinguished from observational “white” noise (Figure 8.4A) and as such is characterized by its

variability. In contrast, a scaling descriptor exhibiting scaling properties will be in homogeneous in

space or in time (Figure 8.4B). Now, considering that an ecological entity is a pattern bounded in

space or in time (Cousins 1988), an inhomogeneous descriptor can then be regarded as a structural

ecological entity. As a consequence, heterogeneity will not be applied to the variability of a given

descriptor in space or in time as widely done (see, for example, Kolasa and Pickett 1991) but instead

to patterns or processes exhibiting different levels of structures (that is, inhomogeneity) over space

or time and hence corresponding to different driving processes.

Box 8.1 tERMInoLoGICAL AMBIGuItIES In SCIEnCE

Terminological ambiguities are not specic to ecological sciences but seem to be the rule in

science in general. To assess this issue, all papers reporting the term variability, homogene-

ity, heterogeneity, inhomogeneity, and intermittency that appeared in the journals Nature

and Science, and under the ScienceDirect banner of Elsevier from 1998 to 2008, were

scrutinized.

2782.indb 255 9/11/09 12:15:01 PM

256 Fractals and Multifractals in Ecology and Aquatic Science

This is exemplied using some of the results obtained in the previous sections. For instance, the

distributions of temperature and salinity investigated in the inshore waters of the eastern English

Channel (Section 4.2.1.3.2, Figure 4.9A,B,D,E) are homogeneous as they exhibit a scaling behav-

ior (or a lack of scaling behavior) over the whole range of investigated scales (Figure 4.9A,B and

Figure 8.4A,B). In contrast, the distribution of in vivo uorescence is heterogeneous as it exhibits

two distinct scaling ranges (Figure 4.9C and Figure 8.4C,D). The isotropy of the fractal dimensions

derived from the two-dimensional pattern of microphytobenthos biomass shown in Figure 7.9A,B

(Section 7.2.2) leads us to consider this pattern as homogeneous (Figure 8.4E). A pattern leading to

fractal anisotropy would be, in turn, qualied as being heterogeneous (Figure 8.4F). Finally, the frac-

tal stationarity and nonstationarity exhibited respectively by temperature and salinity time series and

by uorescence time series (Figure 7.10; Section 7.2.3.2) lead us to consider the temporal pattern of

temperature and salinity as temporally homogeneous (Figure 8.4E), while uorescence is temporally

heterogeneous (Figure 8.4F). These previous examples clearly indicate that a descriptor inhomoge-

neous (or not) in space or in time can be either homogeneous or heterogeneous in space or in time.

From the 63,233 papers resulting from this survey (Table 8.B1.1), it appears that variability

and homogeneity are consistently used to described the uctuations and the absence of uctua-

tions in the distribution of any parameter; see, for example, Porter and Semenov (1999) and

Schindell et al. (1999). In contrast, the terms heterogeneity and inhomogeneity are vaguely

dened, while the seldom-used term intermittency has a more constant meaning (see Section

8.1.3.3). The term heterogeneity is, however, mostly used to describe the uctuations, that is, the

variability (Kolasa and Rollo 1991; Merriam-Webster’s Collegiate Dictionary 2008), of a given

process, as “velocity heterogeneity” or “temperature heterogeneity” in the Earth’s core (Sumita

and Olson 1999; Vidale and Earle 2000), as widely done by many biologists and ecologists

(Mitchell and Furhman 1989; Rainey and Travisano 1998). Heterogeneity seldom ts the basic

denition of different entities or kinds of elements (Kolasa and Rollo 1991; Merriam-Webster’s

Collegiate Dictionary 2008), and when it is the case, the corresponding papers are most of

the time related to ecological sciences (Guegan et al. 1998). In particular, this demonstrates

that such terminological ambiguities are far from being an ecological specicity, and that eco-

logical sciences are nally not so badly off. On the other hand, the very violent and a priori

unpredictable uctuations perceptible in turbulent velocity and scalar elds, nancial markets

uctuations, or medical sciences are systematically described in terms of intermittency, thus

describing a specic kind of variability, and opposed to homogeneity (Shraiman and Siggia

2000; Helmlinger et al. 2000). Finally, the concept related to inhomogeneity refers without dis-

tinction to the variability of a given descriptor, for example, “the isotopic inhomogeneity of this

material: the variability in its sulfur-34/sulphur-32 isotope ratio” (Coplen and Krouse 1998), its

heterogeneity (Bonn et al. 1998) sensu Kolasa and Rollo (1991), its nonhomogeneity (Wu et al.

1999), or its intermittency (Jiménez 2006).

Nature

Science

ScienceDirect

Variability

Homogeneity

Heterogeneity

Inhomogeneity

Intermittency

Abstract

Title

402

218

Title

Abstract

232

Title

6,799

445

2,620

321

135

Abstract

29,070

7,194

13,188

1,967

443

—

table 8.b1.1

bibliographic survey of all Papers reporting the terms Variability,

Heterogeneity, Inhomogeneity, and Intermittency in their title or

abstract from 1998 to 2008

2782.indb 256 9/11/09 12:15:03 PM

From Fractals to Multifractals 257

The previous propositions suggest some terminological specications in comparison with basic

systemic approaches. For instance, hierarchical approaches, initially developed in the framework of

landscape analysis, have been devoted to describe “how heterogeneity changes with scale”

(Allen

and Starr 1982). On the other hand, following our approach, a system considered as being hierarchi-

cal must be viewed as a heterogeneous system presenting different scales of inhomogeneity. In that

way, the main point of hierarchical theory should be instead regarded as the way to describe how

inhomogeneity changes with scales. Moreover, the concepts developed in the present chapter could

also be regarded as a way to complement hierarchical approaches in the sense that they allow us to

describe how the structure of a given descriptor, hierarchical (Figure 8.4C,D) or not (Figure 8.4E,F),

evolves in time or in space. These concepts could subsequently provide an efcient framework to

reconcile space- and time-oriented approaches. Indeed, a descriptor exhibiting different inhomo-

geneous structure will be regarded as being heterogeneous, the inhomogeneity uctuating either in

space or in time, which is still actually not widely done (Kolasa and Rollo 1991; Naeem and Colwell

1991; Shachak and Brand 1991; Levin et al. 1993).

8.1.5 in T u i T i v E mu l T i F r a c T a l s F o r Ec o l o g i s T s

Before reviewing and illustrating the traditional multifractal methods in Section 8.2, a method that

is believed to be much more intuitive to nonmathematically oriented readers will be introduced.

Consider the spatial distribution of microphytobenthos biomass at spatial scales ranging from

Log E(x)

Log E(x) Log E(x)

Log x

Figure 8.4 Schematic illustration of the concepts related to homogeneity, heterogeneity, and inhomogene-

ity, based on the results of a spectral analysis, where E(x) is the spectral density related to a frequency or a

wave number x following that the descriptor is considered in time of in space. A homogeneous descriptor can

either exhibit (A) nonscaling properties (noninhomogeneous descriptor) or (B) scaling properties (inhomoge-

neous descriptor) in time or in space. More specically, an inhomogeneous descriptor can be heterogeneous in

time or in space when it exhibits different scaling regimes, shown in (C, D). A descriptor exhibiting the same

scaling properties (that is, inhomogeneous) over the range of available scales can be homogeneous in time or

in space if its inhomogeneous properties depend on the sampling time or location (E). Similarly, an inhomo-

geneous descriptor can be heterogeneous in space or in time if its inhomogeneous properties evolve with space

or time (F). Y

represents data sets sampled at different times or locations.

2782.indb 257 9/11/09 12:15:05 PM

258 Fractals and Multifractals in Ecology and Aquatic Science

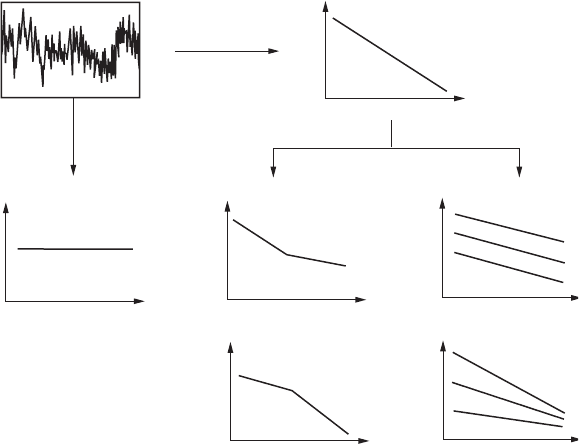
6.67 cm to 1 m (Figure 8.5). Here, a top view of the distribution does not appear as a black and white

“cityscape” but instead as a two-dimensional mosaic (Figure 8.5A). This is because the chlorophyll

concentration is a spatial continuous function rather than a binary one. A three-dimensional view

of the chlorophyll distribution (Figure 8.5B) nevertheless shows similar features with the city

side view (cf. Figure 8.4B). Now the question is: How do we describe simultaneously the different

chlorophyll concentrations and their related scaling properties? The algorithm proposed hereafter

can be regarded as a generalization of the box-counting methods (see Section 3.2.2).

First, one needs to rethink the initial distribution S in terms of n distinct subsets S

such as:

∑

min

max

(8.1)

Chlorophyll (mg · m

–2

)

Chl.

(mg · m

–2

)

Figure 8.5 Concept of multifractality, illustrated considering a two-dimensional pattern of microphytoben-

thos biomass (A) and the related three-dimensional view of the different biomass values (B). Note the similar-

ity with Figure 8.3. The understanding of such a pattern could be limited to “traditional” fractal analysis such

as the patch-intensity dimension (Section 5.2) or surface dimensions (Section 3.2.9), or focus on the distribu-

tion of each different biomass (see Figure 8.6).

2782.indb 258 9/11/09 12:15:10 PM

From Fractals to Multifractals 259

where C

min

and C

max

are the minimum and maximum chlorophyll concentrations of the distribution,

and S

is given as:

SCc

⊂≥()

(8.2)

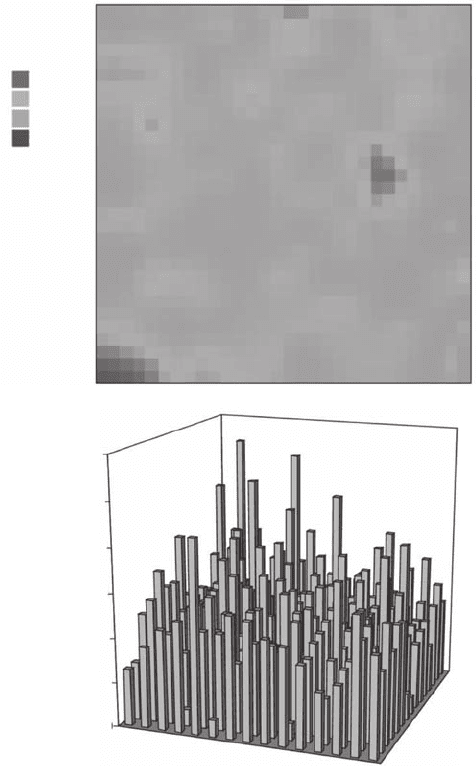
where C is the actual chlorophyll concentration and c a given chlorophyll threshold. This procedure

results in the creation of a set of “black and white” patterns where the white areas correspond to

areas where C ≥ c (Figure 8.6A).

2.0

1.9

1.8

1.7

1.6

1.5

1.4

1.3

1.2

1.1

1.0

26.620.9 22.8 24.719.017.115.213.311.41.9 3.8 5.7 7.6 9.5

Fractal Dimension D

Critical Concentration c

Figure 8.6 Multifractals for ecologists. Using different thresholds, the two-dimensional distribution

shown in Figure 8.5 can be divided in a series of black and white patterns: in black are the areas where the

biomass exceeds a given threshold, and in white are the “empty” areas (A). Each concentration threshold

can then be related to one fractal dimension, the ultimate result being a multifractal function (B) that can

be thought as a characteristic structural property of the pattern. (Modied from Seuront and Spilmont,

2002.)

2782.indb 259 9/11/09 12:15:12 PM

260 Fractals and Multifractals in Ecology and Aquatic Science

Second, standard algorithms aimed at counting the number of boxes of length d occupied by at

least a part of a given set S (see Section 3.2.2) are modied as:

NC c

()≥∝

−

(8.3)

where N

(C ≥ c) corresponds to the number of boxes of length d containing a chlorophyll concentra-

tion greater than a threshold concentration c, and D

the multifractal function associated to the

threshold concentration c. For each threshold concentration c, the slope of the log-log plot of

(C ≥ c) vs. d is an estimate of D

; each threshold concentration c is thus characterized by its own

fractal dimension. Although the increment for threshold c can be arbitrarily selected, it is strongly

recommended that we choose it close to the smallest observed chlorophyll concentration difference

in order (1) to capture the maximum, if not all, of the structure present in set S, and (2) for D

converge to a continuous function. The resulting multifractal function is shown on Figure 8.6B.

The multifractal character of the microphytobenthos biomass distribution shown in Figure 8.5

is ensured by the nonlinear behavior of function D

(Figure 8.6B). The application of Equation

(8.3) to a fractal set S (for example, Brownian or fractional Brownian motions) would have led

to a linear decreasing function (not shown). The shape of the function D

—and in particular

the potential differences in shapes that can be obtained from microphytobenthos distribution, for

example, at different seasons or from sandy and muddy ats sampling—can then be used as an

ecological structural index. The main advantage of such an approach when compared to the fractal

framework is that the overall complexity present in a given data set can be fully quantied. This is

particularly relevant in the framework of behavioral biology and ecology. Indeed, prey distribution

is very important for predators because food availability changes depending on the fractal dimen-

sion. Low fractal dimensions indicate a smooth and predictable distribution of particles gathered in

small numbers of patches, while high fractal dimensions indicate rough, fragmented, space-lling

and less predictable distributions. Therefore, when a predator can remotely detect its surroundings,

prey distributions with low dimension should be more efcient. In contrast, when a predator has

no remote detection ability, prey distributions with high dimension should be preferable, because

available food quantity or encounter rates become proportional to the searched volume as fractal

dimension increases. As a consequence, because the high-density patches are expected to be the

most valuable in terms of energy budget, the specic knowledge of their fractal dimension can be a

crucial way to improve our understanding of predator–prey interactions in ecology.

8.2 methods For multiFractals

8.2.1 g

E n E r a l i Z E d co r r E l a T i o n di m E n s i o n Fu n c T i o n D(q) a n d T h E ma s s Ex p o n E n T s t(q)

8.2.1.1 theory

Consider a D

-dimensional space (the support of the measure m, for instance, the height of buildings in

a city; see Section 8.1.1 and Figure 8.3), which is divided into D

-dimensional boxes of size d, then:

() ()

δµδ

∑

(8.4)

denotes the integrated measures on the ith cube of edge d (in an ecological example, the probability

of nding an organism in this volume). One can then dene the qth-order moment of the probability

distribution (or “partition function”) M

(d) (Halsey et al. 1986):

() ()

()

δδ

∑

(8.5)

2782.indb 260 9/11/09 12:15:16 PM

From Fractals to Multifractals 261

where N(d) in the number of boxes of size d. The information dimension (Equation 3.34) and the

correlation dimension (Equation 3.41) can then be written as:

() log()

δδ

−

(8.6)

and

() lim

()

log( /)

→

(8.7)

where I

(d) and D(q) are the generalized information dimension (or Reyni information of qth order;

Rényi 1970) and the generalized correlation dimension (Grassberger 1983; Hentschel and Procaccia

1983), respectively. Note that the generalized correlation dimension D(q) is conceptually similar to

the multifractal function D

introduced in Section 8.1.5.

From Equation (8.5) through Equation (8.7), one readily nds the previously dened box dimen-

sion (see Section 3.2.2, Equation 3.15), the information dimension (see Section 3.2.5, Equation

3.34), and the correlation dimension (see Section 3.2.6, Equation 3.41) for integer q as special cases.

The box dimension, the information dimension, and the correlation dimension are then respectively

given as:

DDqD

→

lim()()

(8.8)

DDqD

→

lim () ()

(8.9)

and

DDqD

cor

→

lim()()

(8.10)

The generalized dimension function D(q) is dened for all real values of q and is estimated as the

slope of the log-log plot of I

(d) vs. d. For monofractal sets, the function D(q) is a linear function

of q; in other words, no additional information is gained by examining higher moments, that is,

more extreme values of the measure m. Alternatively, for multifractal sets, D(q) is a nonlinear function

of q. Note that there are lower and upper limiting dimensions, D

−∞

and D

+∞

, which are related to the

regions of the set where the measure m is sparser and denser, respectively. For positive values of q,

D(q) reects the scaling of the large uctuations and strong singularities. In contrast, for negative

values of q, D(q) reects the scaling of the small uctuations and weak singularities (Vicsek 1993;

Takayasu 1997).

Remember that for a given value of d, the mass m(d) (see Equation 3.26) is expressed as the

rst moment (that is, the mean) of the probability distribution, Equation (8.5) can be equivalently

written as:

(d) ∝ d

−t(q)

(8.11)

2782.indb 261 9/11/09 12:15:20 PM

262 Fractals and Multifractals in Ecology and Aquatic Science

where t(q) is a mass exponent function. For monofractal sets, t(q) is linear, t(q) = qH − 1, where H

is the Hurst exponent. In contrast, multifractal sets display a nonlinear function t(q). Note that t(q)

is related to the spectral exponent b as:

βτ

=+22()

(8.12)

Moreover, for multifractal sets, Equations (8.6), (8.7), and (8.11) lead to:

() ()()qqDq=−1

(8.13)

Note that for q = 0, D(q) = t(q) = D(0) and t(1) = 0. Combining Equations (8.12) and (8.13) nally

leads to:

b = 2 + D(2) (8.14)

where D(q) is the generalized correlation dimension (see Equation 8.7), and b is the spectral exponent.

8.2.1.2 application: salinity stress in the cladoceran Daphniopsis Australis

The cladoceran Daphniopsis australis (Sergeev and Williams 1985) is endemic to saline lakes and

swamps of the southeast of Australia and is adapted to salinities ranging from 4 to 30 PSU (Sergeev

and Williams 1985). Despite the potential keystone role of this species in the structure and function

of South Australian inland water ecosystems, there have been few ecological studies on this genus

and none on this particular species. In particular, nothing is known on the effect of extreme salini-

ties (that is, up to 160 PSU) (Schapira et al. 2009) occurring in summer in relation to evaporation on

their biology and ecology. Here the swimming behavior of D. australis is investigated at a known

optimal salinity (22 PSU) and in the case where S = 50 Practical Salinity Unit (PSU).

Individuals of D. australis were continuously cultured at Flinders University (South Australia)

in 20-liter containers and fed on the phytoplankton Isochrysis Tahitian under constant conditions

of temperature (22°C) and salinity (22 PSU) on a 12-hour light–dark cycle. Behavioral experiments

were conducted on individual males following Seuront (2006), and their successive displacements

analyzed using the generalized dimension function D(q) (Equation 8.7) and the mass exponent func-

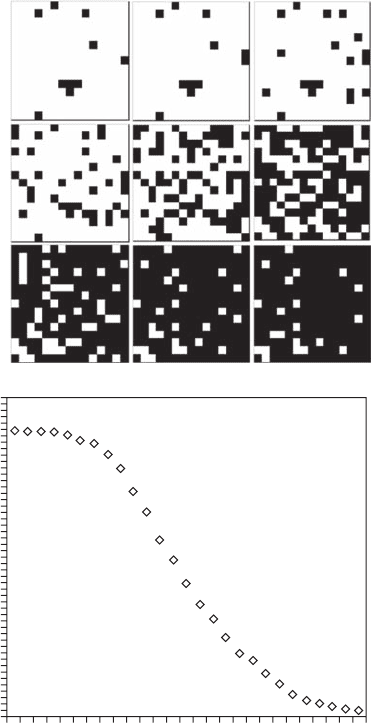
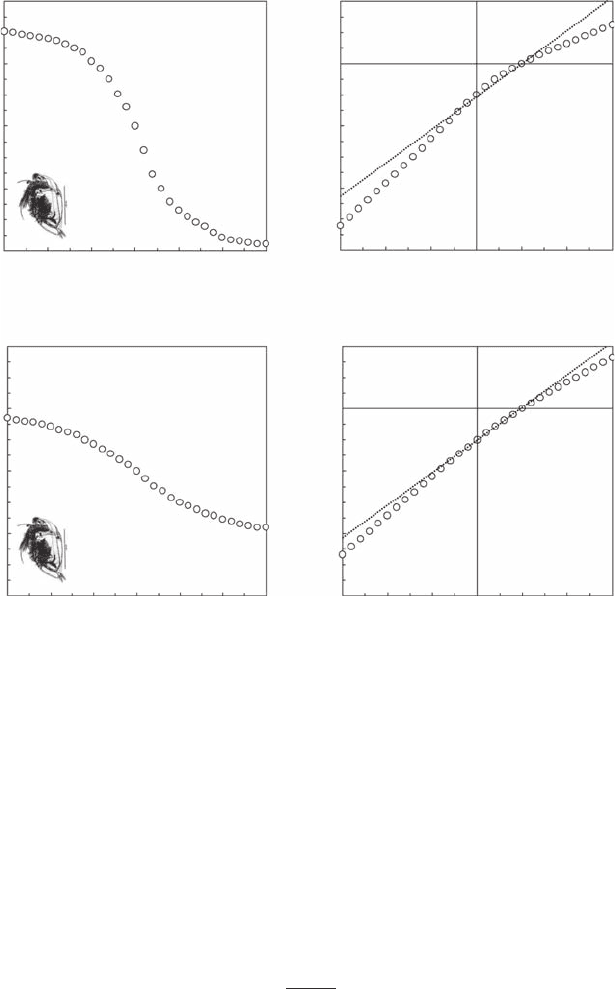
tion t(q) (Equation 8.11). The functions D(q) and t(q) clearly exhibit a multifractal signature under

optimal salinity conditions (S = 22 PSU) (Figure 8.7A,B). In contrast, for S = 50 PSU, both functions

indicate that the successive displacements of male D. australis have weaker multifractal properties

(Figure 8.7C,D). This is consistent with and generalizes previous results showing a decrease in the

complexity of behavioral sequences under stressful conditions for a range of organisms (Section

4.2.2.2) (Alados et al. 1996; María et al. 2004; Alados and Huffman 2000; Seuront and Leterme

2007). A shift between multifractal and fractal properties—or, more generally, a change in mul-

tifractal properties in animal behavior—is then suggested as a potential diagnostic tool to assess

animal stress levels and health. This specic issue is explored further in Section 8.2.2.

8.2.2 mu l T i F r a c T a l sp E c T r u m f(a)

8.2.2.1 theory

The number

µδ

log()

log

, also referred as to the Hölder exponent, is the singularity strength of the

ith box. This exponent may be interpreted as a crowding index of a measure of the concentration

(accumulation) of m: the greater a

is, the smaller the concentration of the measure, and vice versa.

For every box size d, the numbers of cells N

(d) in which the Hölder exponent a

has a value within

the range [a, a + da] behave like:

(d) ∝ d

−f(a)

(8.15)

2782.indb 262 9/11/09 12:15:23 PM

From Fractals to Multifractals 263

Thus, f(a) corresponds to the fractal dimension of the subset in which a

equals a; that is, f(a) char-

acterizes the abundance of cells with Hölder exponent a and is called the singularity spectrum of

the distribution. The singularity spectrum f(a) and the mass exponent function t(q) are connected

via a Legendre transform as (Evertsz and Mandelbrot 1992):

()

(8.16)

and

fqqq q(()) () ()

αατ

=−

(8.17)

Considering the relationship between the mass exponent function t(q) and the generalized dimen-

sion function D(q) (cf. Equation 8.13), the singularity spectrum f(a) contains exactly the same infor-

mation as t(q) and D(q).

1.4

1.2

1.0

0.8

0.6

–3

–2

–1

0123 –3

–2

–1

0123

–2

–6

–4

τ(q)

–2

–4

–6

τ(q)

D(q)

1.4

1.2

1.0

0.8

0.6

D(q)

–3

–2

–1

0123 –3

–2

–1

0123

Figure 8.7 Generalized dimension function D(q) and the mass exponent function t(q) estimated from the

successive displacements of male Daphniopsis australis under contrasted conditions of salinity; that is, (A, B)

S = 22 PSU, and (C, D) S = 50 PSU. The multifractality of D. australis swimming behavior—that is, the non-

linearity of D(q) and t(q)—is stronger under low salinity conditions. Note that for q = 0, D(q) = t(q) = D(0),

D(0) being the fractal dimension of the support of the measure, and q = 1, t(q) = 0. The dashed lines (B, D) are

the functions t(q) expected in case of monofractality.

2782.indb 263 9/11/09 12:15:27 PM