Сергеев В.Л. Интегрированные системы идентификации
Подождите немного. Документ загружается.

61
Условие 3. Случайные величины ξ и η взаимно независимы
() ( )( )0,1,,1,
ij i i j j
Cov M M M i n j m=− −===ξη ξ ξ η η
.
Условие 4. Ошибки измерения вектора входных переменных х малы,
и их действием можно пренебречь
*
(
=
+Δxx x, где 0, 1).
Δ
=Δ<<Mx Dx
Условие 5. Ранг матрицы планирования
T
FFравен размерности век-
тора оцениваемых параметров
,().m Rank m
=
F
Определитель и собст-
венные числа
,1,
j
j
m
λ
= матрицы
T
FF
не равны нулю.
Условие 6. Объем выборки n вектора измерений выхода объекта не
меньше числа оцениваемых параметров,
.nm≥
Дополнительно будем считать, что элементы матрицы
F и парамет-
ры модели исследуемого объекта α – неслучайные величины.
Для упрощения расчетов перейдем от интегрированной системы
моделей (5.1.3) к ортонормированной интегрированной системе моде-
лей вида
*
,
,
⎧
⎪
⎨
⎪
⎩
=
+
=+
yWγξ
γγη
(5.1.4)
где
1
diag( , ,..., )
T
m
λ
λλ
==WW Λ
– диагональная матрица с элементами
на главной диагонали, равными собственным значениям матрицы ;
T
FF
,,
T
==WFP
γ
Pα P – ортогональная матрица (
T
I
=
PP ).
Для модели (5.1.4) при использовании квадратичных критериев ка-
чества, по аналогии с рассмотренными во второй главе линейными ин-
тегрированными системами идентификации нетрудно получить оценку
вектора параметров
γ
:
*1*
()( )( )
TT
y
−
=+ +γ KWWKWyKγ
, (5.1.5)
где
12
diag( , , ..., )
m
K
KK=K – диагональная матрица весовых функций,
учитывающих влияние дополнительных априорных сведений
γ
.
Отметим, что при K = 0 из (5.1.5) следует оценка метода наимень-
ших квадратов
*1*
(0) ( )
TT
−
=γ WW Wy.
Сформулируем теоремы, определяющие СКОА оценок (5.1.5) и оп-
тимальную структуру весовых функций
12
diag( , , ..., )
m
K
KK
=
K .
Теорема 1. При выполнении приведенных выше стандартных усло-
вий функционирования системы среднеквадратическая ошибка аппрок-
симации оценки (5.1.5) примет вид
2222
*
2
1
λσ (σε)
δ ()
(λ )
m
jj j
j
jj
K
K
η
ξ
=
+
+
=
+
∑
γ K
, (5.1.6)
где
εγγ
j
jj
M
=−
– величина смещения дополнительных априорных дан-
ных
γ
j
относительно истинного значения оцениваемого параметра
62
γ ;λ ,1,
jj
j
m=
– собственные значения (числа) матрицы
2
ξ
; σ
T
FF
и
2
η
σ
–
дисперсии случайных величин ξ и η соответственно.
При 0=K из (5.1.6) следует дисперсия оценок метода наименьших
квадратов
2
ξ
**
1
,
σ
δ (0) (0)
λ
m
j
j
D
=
==
∑
γγ
(5.1.7)
которая является минимально возможной, достигающей нижней грани-
цы неравенства Рао-Крамера (см. приложение 5 ) в классе линейных не-
смещенных оценок.
Для доказательства теоремы 1 достаточно вычислить дисперсию и
квадрат смещения оценки
*
()
γ
Κ (5.1.5), которую с учетом усло-
вия
T
12
diag(λ , λ , ..., λ )
m
==WW Λ представим в виде
T*
*
()()
γ () , 1,.
λ
jj
j
jj
K
jm
K
+
==
+
Wy Kγ
( 5.1.8)
Учитывая, что
T* T * 2
ξ
D( ) ( D ) λσ
jjj
==Wy WW y ,
22
η
D( , ) σ ,1,
jj
K
jm==K γ ,
приведем выражение для дисперсии оценок (5.2.8)
222
η
ξ
*
2
λσ σ
Dγ () , 1,
(λ )
jj
j
jj
K
K
jm
K
+
==
+
, (5.1.9)
где
mj
j
,1, =λ – собственные числа матрицы
T
FF.
Для определение квадрата смещения оценки (5.1.5) достаточно вы-
числить величину
2
T*
*2
M( ) M( )
(Mγ ()γ ),1,
γ
λ
j
jj
j
jj
K
jm
K
⎛⎞
⎜⎟
⎜⎟
⎝⎠
+
−= =
−
+
Wy Kγ
(5.1.10)
с учетом, что случайные величины ξ и η имеют нулевые математиче-
ские ожидания. После несложных преобразований получим
22
*2
2
((
γ
) γ )
(M γγ).
(λ )
jjj
jj
jj
KM
K
−
−=
+
(5.1.11)
Полагая
(γ ) γε
j
jj
M
−=, получим выражение для среднеквадратической
оценки аппроксимации
∑
=
ηξ
+λ
ε+σ+σλ
=δ
m
j
jj
jjj
K
K
1
2
2222
*
)(
)(
)(Kγ
,
что и доказывает теорему 1.
63
Теорема 2. Существуют такие оптимальные значения весовых
функций
0
,1,
j
K
jm= , при которых выполняется неравенство
)0()(
*0*
γKγ δ≤δ
(5.1.12)
.,1,
)(
)(minarg
22
2
*0
mjK
j
K
j
j
=
ε+σ
σ
=δ=
η
ξ
Kγ
Эффективность оценок параметров интегрированной системы мо-
делей с учетом априорной информации определяется соотношением
*2
ξ
**0
022
η
δγ (0) σ
(γ (0), γ ()) 1 , 1,.
δγ () λ (σε)
j
jj j
jjj
eK jm
K
==+ =
+
. (5.1.13)
Из формулы видно, что при определенных значениях
222
η
ξ
σ , σ , ε , λ ,1,
jj
j
m= , оценки параметров линейной интегрированной
модели могут быть эффективнее оценок метода наименьших квадратов.
Следует также отметить, что при оптимальных значениях весовых
функций
2
ξ
0
22
η
σ
,1,
(σε)
j
j
K
jm==
+
(5.1.14)
оценки
*0
()
γ
K
параметров, полученных на основе использования ин-
тегрированных моделей, не могут ухудшать свойства классических оце-
нок метода наименьших квадратов, они могут их только улучшать.
Доказать теорему 2 нетрудно по следующей схеме:
1. Находим оптимальные значения весовых функций
0*
arg min δγ (), 1,.
j
jjj
K
K
Kj m==
.
2. Находим среднеквадратическую ошибку аппроксимации при оп-
тимальных весовых функциях (5.1.12)
0
20222
ξη
02
*0
()
λσ ()(σε)
δγ .
(λ )
j
jj
jj
j
j
K
K
K
++
=
+
3. Находим отношение ошибок
,,1,
)(
)0(
0*0
0
mj
K
e
jj
j
=
γδ
δ
=
где
0
δ (0) – СКОА оценок параметров метода наименьших квадратов,
)(
0*0
jj
Kγδ
– СКОА оценки (5.1.5) при оптимальных весовых функциях.

64
Для иллюстрации поведения среднеквадратической ошибки ап-
проксимации (5.1.6) рассмотрим в качестве примера простую интегри-
рованную систему моделей вида:
*
γ
,
γ
γ + ε + η,
⎧
⎪
⎨
⎪
⎩
=+
=
y ξ
(5.1.15)
где полагаем, что дисперсия ошибок измерения выхода объекта равна
единице (
2
ξ
σ = 1), дисперсия ошибок задания дополнительной информа-
ции о параметре объекта γ равна
2
η
σ 0,3
=
; квадрат смещения значения
дополнительной информации о параметре модели исследуемого объекта
γ относительно оцениваемого значения γ равен
2
ε 0, 25
=
; объем измере-
ний выхода объекта равен двум (n = 2) – для зависимостей, представлен-
ных на рис. 5.1. Для зависимостей, представленных на рис. 5.2, объем
измерений выхода объекта равен пяти (n = 5).
Для интегрированной системы моделей оценка параметра
γ
соглас-
но (5.1.5) примет простой вид:
*
*
1
γ
γ () , 2.
n
i
i
yK
Kn
nK
=
+
=
=
+
∑
(5.1.16)
При значении весовой функции
0
=
К оценка совпадает с оценкой
метода наименьших квадратов, в данном случае с выборочным средним
*
*
1
γ (0) , 2.
n
i
i
y
n
n
=
=
=
∑
(5.1.17)
При значении дополнительной информации о параметре, равном
нулю
γ 0= , оценка (5.1.11) совпадает c Ridge-оценкой
*
*
1
γ () , 2.
n
i
i
y
Kn
nK
=
=
=
+
∑
(5.1.18)
Выражения для среднеквадратической ошибки аппроксимации
приведенных выше оценок согласно формуле (5.1.6) примут соответст-
вующий вид:
*2222 2
η
ξ
δγ ()(σ (σ + ε )) / ( )
K
nK nK=+ +, (5.1.19)
n/)0(
2*
ξ
σ=δγ
, (5.1.20)
22*
)/()( KnnK +σ=δγ
ξ
. (5.1.21)
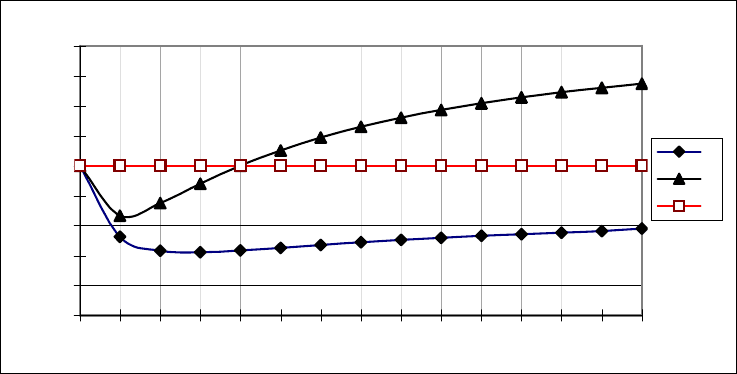
На рис. 5.1 и 5.2 приведены зависимости, отражающие поведение
среднеквадратических ошибок аппроксимации, оценки параметра ин-
65
тегрированной системы моделей (5.1.19), (5.1.21) в зависимости от зна-
чений весовой функции К.
Из рис. 5.1 и 5.2 видно, что существуют оптимальные значения весо-
вой функции
0
2
K
=
и
0
1
K
=
, при которых достигается максимальная
точность оценок (2.2.21). Оценка (5.1.19), учитывающая дополнительную
информацию, имеет пологий минимум и остается эффективнее оценок
метода наименьших квадратов и Ridge-приближений в достаточно широ-
кой области изменения весовой функции K. Условно назовем данную об-
ласть значений весовой функции ΔK = K
2
– К
1
(K
1
< K
0
< K
2
) – областью
эффективности оценок, где точность оценок меняется незначительно от-
носительно наименьшего, оптимального значения. Фактически опти-
мальные свойства оценок сохраняются при значительном изменении ве-
совой функции K.
0,00
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
K
δ
3
2
1
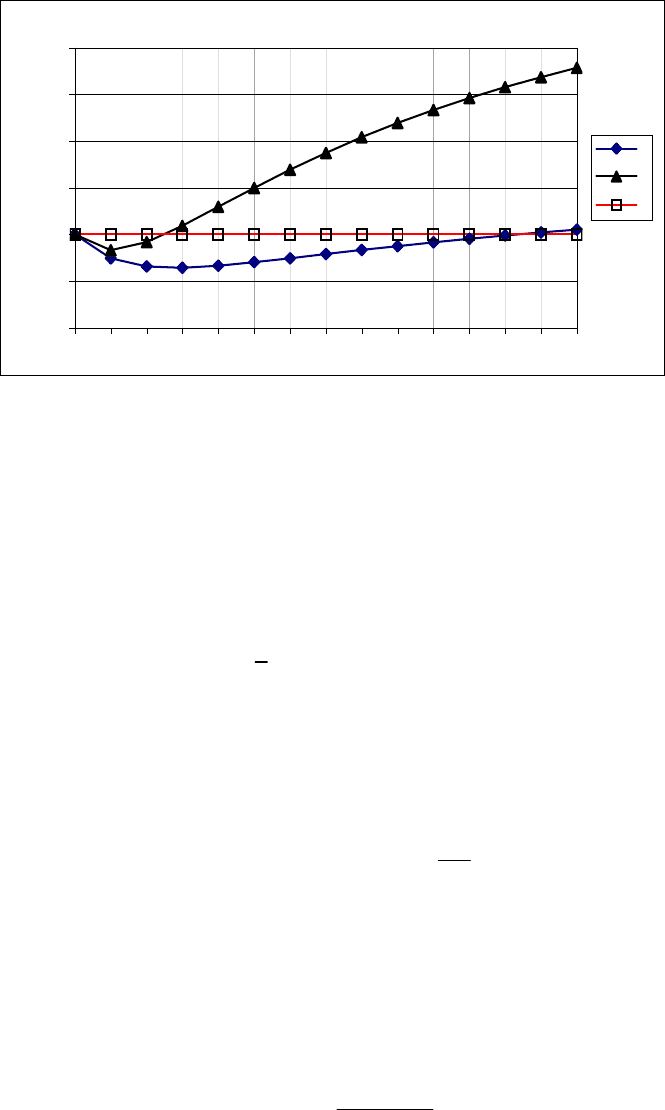
Рис. 5.1. Зависимость поведения точности оценок (5.1.19) – (5.1.21)
от значения весовой функции К при объеме выборки n = 2:
1 – среднеквадратическая ошибка аппроксимации (СКОА) оценки метода
наименьших квадратов; 2 – CКОА Ridge-приближения; 3 – СКОА оценки с учетом
дополнительной априорной информации об оцениваемом параметре
При увеличении объема выборки до пяти значений n = 5 (рис. 5.2)
точность всех рассматриваемых оценок повышается. Оптимальные зна-
чения весовых функций не меняются, а область эффективности оценок
K
Δ сужается, особенно для Ridge-приближения.
Следует также отметить, что в области эффективности ΔK всего
при двух измерениях выхода объекта оценка с учетом дополнительной
априорной информации обладает такой же точностью (см. рис. 5.1, ли-
ния 3), как и оценка метода наименьших квадратов при пяти измерениях
(см. рис. 5.2, линия 1).
66
0,00
0,10
0,20
0,30
0,40
0,50
0,60
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
K
δ
3
2
1
Рис. 5.2. Зависимость поведения точности оценок (5.1.19) – (5.1.21)
от значения весовой функции К при объеме выборки n = 5:
1 – среднеквадратическая ошибка аппроксимации (СКОА) оценки метода
наименьших квадратов; 2 – CКОА Ridge-приближения; 3 – СКОА оценки с учетом
дополнительной априорной информации об оцениваемом параметре
Рассмотрим вопросы точности рассмотренных в третьей главе оце-
нок параметров нелинейных интегрированных систем моделей вида
*
(,) ,
.
⎧
⎪
⎨
⎪
⎩
=
+
=+
yfxa
ξ
ααη
(5.1.22)
Известно, что для данной модели алгоритм определения вектора
неизвестных параметров
α c использованием метода Гаусса–Ньютона
сводится к последовательному решению систем линейных уравнений
(3.1.6), (3.1.8) на основе рекуррентной процедуры:
11
11 1
,
( β )(β ), 1,2,3,....
ii i
i
TiiT i
yy
h
i
−−
−− −
⎧
⎪
⎨
⎪
⎩
=+Δ
+⋅ Δ = +⋅ Δ =
αα
αα α
DWD W α DWe W α
(5.1.23)
Под точностью оценок (5.2.23) будем понимать среднеквадратиче-
скую ошибку аппроксимации
*
αδ
, где под α
*
будем понимать прибли-
жение
i
α с номером i , попавшее в область, для которой справедливо ли-
нейное разложение функции (,)
f
xa в ряд Тейлора в окрестности истин-
ного значения параметра
α
и
)(
),(
),(),(
и
*
и
1
*
и
*
jj
m
j
j
f
f α−α
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
α∂
∂
+≈
∑
=
αx
αxfαx
, (5.1.24)
где индекс «и» у частных производных означает, что они вычислены в
точке
и
α . С учетом (5.2.24) представим нелинейную интегрированную
систему моделей (5.2.22) в линеаризованном виде относительно вектора
приращений параметров Δ
α
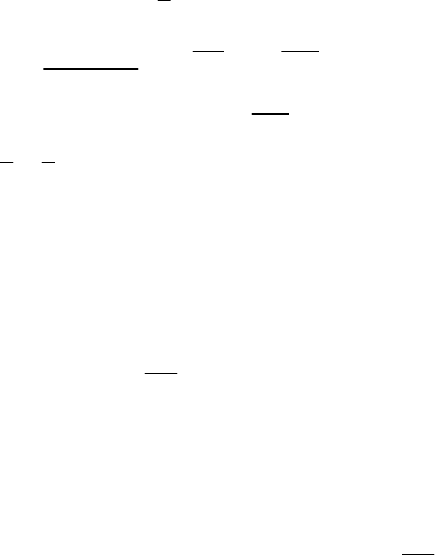
67
*
,
,
и
⎧
⎪
⎨
⎪
⎩
=
Δ+
Δ=Δ+
eDαξ
ααη
(5.1.25)
**
(, ),
и
=−eyfxα
(,)
, 1, , 1,
α
i
и
j
и
injm
⎛⎞
⎜⎟
⎜⎟
⎝⎠
∂
===
∂
fx α
D
– матрица частных про-
изводных по параметрам
α , 1,
j
j
m
=
, вычисленная в точке
и
α ,( )
и
Δ= −ααα,
и
Δ
=−ααα.
Введем ортогональные преобразования
и
P,
T
=
Δ=ΔVD bPα
, (5.1.26)
где Р – некоторая ортогональная матрица, и перейдем к ортонормиро-
ванной линеаризованной интегрированной системе моделей
*
,
,
⎧
⎪
⎨
⎪
⎩
=
Δ+
Δ
=Δ +
eVbξ
bbη
(5.1.27)
где
),...,,diag(
1 m
T
λλλ== ΛVV
– диагональная матрица с элементами на
главной диагонали, равными собственным числам матрицы V .
По аналогии с оценкой параметров линейной системы (5.1.4) нетруд-
но получить соответствующие выражения и для оценок параметров bΔ :
*T 1*
()( )( )
yy
−
Δ= + +ΔbK VWV K VWe Kb
. (5.1.28)
С учетом (5.2.24) оценку параметров нелинейной интегрированной сис-
темы (5.1.22) можно представить в виде
**
() ()
T
и
=
+Δα K α PbK. (5.1.29)
Таким образом, в случае достаточной близости параметров
*
α к ис-
тинным значениям
и
α в области, где справедливо разложение (5.1.24),
задача определения параметров нелинейной интегрированной системы
моделей аналогична задаче определения параметров линейной интегри-
рованной системы.
В этой связи имеют место и условия нормального функционирова-
ния системы, при выполнении которых выражение для СКОА линейных
и нелинейных оценок совпадают и равны (5.1.6).
5.2. Критерии качества интегрированных систем идентификации
в экстремальных ситуациях
Проведенный в предыдущем параграфе анализ точности и эффек-
тивности характеризует качество оценок параметров интегрированных
систем моделей с учетом дополнительной априорной информации в
стандартных условиях нормального функционирования системы. В ре-
альных условиях при возникновении определенных экстремальных си-
туаций стандартные допущения могут частично либо полностью не вы-
полняться.
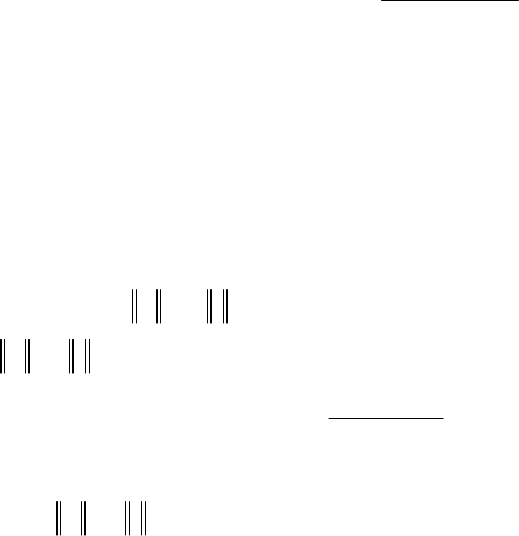
68
В экстремальных ситуациях многие оценки теряют свою эффектив-
ность и часто становятся неработоспособными. Например, оптимальные
в стандартных условиях оценки метода наименьших квадратов только
при нарушении шестого условия из группы условий, приведенных в
предыдущем параграфе, становятся неэффективными и неработоспо-
собными в силу плохой обусловленности матрицы
T
FF
.
Причинами нарушения шестого условия нормального функциони-
рования системы могут быть достаточно много ситуаций, которые зара-
нее трудно предвидеть и, следовательно, проконтролировать. Это могут
быть причины, связанные с ошибками округления, реализацией числен-
ных методов на вычислительных машинах, недостаточным объемом
экспериментальных данных и рядом других причин.
В реальных условиях функционирования систем при
возникнове-
нии определения экстремальных ситуаций, стандартные предпосылки
могут частично либо полностью не выполняться.
Для сравнения эффективности оценок параметров при нарушении
условий нормального функционирования системы вводится условная
относительная точность
)(/)(
)(/)(
),,,(
*
2
*
1
*
2
*
1
lAα
kAα
lkαα
δ
δ
=e
, (5.2.1)
где
)(/)(
*
1
kAαδ
и
)(/)(
*
2
lAαδ
– СКОА оценок
*
1
α
и
*
2
α
при выполнении
комплекса условий ()Ak и ()Al соответственно. Компоненты вектора
12
(, ,..., )
m
kk k=k принимают значения ноль (0
i
k
=
) либо 1. Компоненты
вектора
12
(, ,..., )
m
ll l=l также принимают значения ноль (0
i
l = ) либо 1.
При 0, ( 0)
ii
kl== условие
i
A
комплекса условий А выполняется. При
1, ( 1)
ii
kl== условие
i
A
не выполняется.
Величины
2
k и
2
l характеризуют степень выполнения условий.
При
22
0==kl
все шесть условий выполняются, и условная относи-
тельная точность
*
**
1
12
*
2
δ /(0)
(, ,0,0)
δ /(0)
e =
α A
αα
α A
совпадает с эффективностью
оценок (5.1.2).
При
22
6==kl все условия нормального функционирования сис-
темы не выполняются.
Пример 1
()
1,6
1, 6
A
A=
– комплекс условий, в котором первое и шестое усло-
вие не выполняются, а все остальные выполняются.

69
Пример 2
0
6
(0,...,0) (0)==AAA
– комплекс стандартных условий нормально-
го функционирования системы. Условия ()Ak будем считать экстре-
мальными, если хотя бы одно условие
1, 1, 6
i
ki
=
∈
комплекса условий
12
(, ,..., )
m
kk k=k не выполняется.
Используя определения условной относительной точности оценок,
введем критерии качества оценок в нестандартных экстремальных си-
туациях.
1. Критерии устойчивости (стабильности) оценок
В качестве меры устойчивости (стабильности) оценки
*
1
α
будем
считать
*
*
1
1
*
10
(δ )/ ( )
(,,0) .
(δ )/
eC
=
<<∞
α Ak
α k
α A
(5.2.2)
Данный критерий характеризует меру потери точности оценки
*
1
α
в
С раз при переходе от стандартных условий
0
A в экстремальные
)(kA
.
2. Критерий эффективности оценок
*
1
α
и
*
2
α
в (нестандартных)
экстремальных идентичных условиях:
*
**
1
12
*
2
δ /()
(, ,)
δ /()
e =
α Ak
ααk
α Ak
. (5.2.3)
3. Примером условной относительной эффективности может
быть относительная эффективность оценки
*
1
α
в нестандартных ус-
ловиях относительно оценки метода наименьших квадратов
*
0
α в стан-
дартных условиях:
0
*
0
*
1
*
0
*
1
/
)(/
)0,,,(
Aα
kAα
kαα
δ
δ
=e
, (5.2.4)
где
*
0
α – оценка метода наименьших квадратов.
Комплексные критерии качества. Сформулируем комплексные
критерии качества оценок в виде следующих определений.
Определение 1. Оценка
*
2
α качественнее оценки
*
1
α , если она ус-
тойчивее оценки
*
1
α и эффективнее в экстремальных ситуациях:
**
**
21
21
**
20 10
(δ )/ ( ) (δ )/ ( )
(,,0) (,,0) ,
(δ )/ (δ )/
eeC=<=<<∞
α Ak α Ak
α k α k
α A α A
(5.2.5)
*
**
1
12
*
2
(δ )/ ( )
(, ,) 1.
(δ )/ ( )
e
=
>
α Ak
ααk
α Ak
(5.2.6)
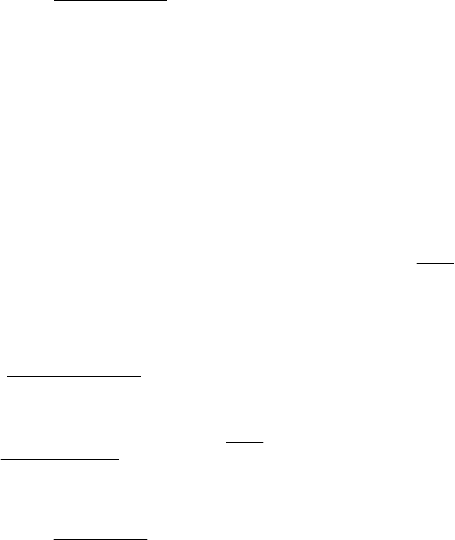
70
Следствие 1. При выполнении условий (5.2.5), (5.2.6) немедленно
следует условие эффективности оценок в классическом (узком) смысле
*
**
10
12
*
20
(δ )/
(, ,0) 1.
(δ )/
e
=
>
α A
αα
α A
(5.2.7)
Если оценка
*
2
α стабильнее и точнее
*
1
α в экстремальных условиях
()Ak , она и точнее (эффективнее в классическом смысле) оценки
*
1
α
в стандартных условиях. Обратное утверждение неверно.
Следует отметить, что часто проверяется условие эффективности в
узком смысле (5.2.7), выполнение которого ничего не говорит о ста-
бильности, а следовательно, и о качестве оценок.
Определение 2. Оценка
*
α среди устойчивых оценок
*
,1,
j
j
m=α
на-
зывается качественной, если выполняются условия:
*
*
1
*
0
(δ )/ ( )
(,,0) ,
(δ )/
eC
=
<<∞
α Ak
α k
α A
(5.2.8)
*
**
*
δ /()
( , , ) 1, 1, ,
δ /()
j
j
ejm=>∀=
α Ak
ααk
α Ak
(5.2.9)
*
**
00
02
*
0
δ /
(, ,0) ,
δ /
eC==
α A
αα
α A
(5.2.10)
*
20
1,C = α
– оценка метода наименьших квадратов.
Оценка является качественной, если она устойчива, эффективна в
экстремальных ситуациях и не уступает по эффективности оценке мето-
да наименьших квадратов. При
2
1C >
оценку будем называть высокока-
чественной.
Живучесть оценок. Введем понятие живучести оценок. Качество
оценок связано с величиной
r (
1 rm
≤
≤
), где r – количество не выпол-
няющихся условий нормального функционирования системы (количе-
ство экстремальных, одновременно имеющих место, ситуаций). Чем
больше
r, при которых выполняются условия качества оценок (5.2.8),
(5.2.10), тем более качественная оценка. Оценка обладает максималь-
ным качеством, если она стабильнее и точнее любых других оценок при
максимальном числе экстремальных условий
.rm
=
Пусть
() rR
– множество всех качественных оценок α
*
, для кото-
рых выполняются условия (5.2.8).
Определение 3. Оценка α
*
называется живучей, если
*
()r
∈
α R при 1r ≥ , (5.2.11)
где
r – уровень живучести.
