Сергеев В.Л. Интегрированные системы идентификации
Подождите немного. Документ загружается.

11
Статистические свойства случайной составляющей
ξ
в общем слу-
чае зависят от контролируемого входа X.
Модель объекта и в этом случае строится в общем случае в виде
нелинейной многомерной функции регрессии вида
)(xFY
=
, (1.2.6)
которая не зависит от неконтролируемой случайной составляющей ξ.
8. Непараметрические стохастические модели. Непараметриче-
ские статические стохастические модели описываются функцией, отно-
сительно которой известны лишь достаточно общие сведения, такие как
непрерывность, ограниченность, существование производных и т. д.
При данных априорных предположениях в качестве модели объекта
часто используют функцию регрессии (условное математическое ожи
-
дание)
1
() ( / )d
R
yf yPy y==
∫
xx
, (1.2.7)
где
)/( xyP
– условная плотность вероятности выхода объекта.
Задача идентификации в данном случае заключается в оценке ус-
ловной плотности вероятности и функции регрессии на основе наблю-
дений входа и выходов объекта.
Динамические модели
В качестве математического описания динамических объектов наи-
более часто используют интегральные уравнения, обыкновенные диф-
ференциальные уравнения, дифференциальные уравнения в частных
производных, конечно-разностные, дискретные аналоги интегральных и
дифференциальных уравнений.
1. Динамические системы на основе интегральных уравнений. Мо-
дель линейного динамического объекта, на вход которого поступает
сигнал
)(tx , вызывающий реакцию )(ty , часто представляют в виде ин-
тегрального уравнения:
() (, ) ( )d
t
yt ht x
−
∞
=
τττ
∫
, (1.2.8)
где
()
τ,th
– импульсная переходная функция (ИПФ) системы,
()
0τ,
=
th
при
τ<
t
.
В стационарном случае
(, ) ( )ht ht
τ
=−τ
уравнение (8) переходит в
интегральное уравнение свертки
()
0
( )()d ()( )d.
t
yt ht x h xt
∞
−∞
=−τττ=τ−ττ
∫∫
(1.2.9)

12
Задача идентификации заключается в определении импульсной пе-
реходной функции (ИПФ) объекта
(
)
τ,th
либо
(
)
h
τ
.
Наряду с описанием линейного объекта с помощью ИПФ можно
использовать его описание с помощью передаточной функции
()
,tpϕ
,
связанной с ИПФ соотношениями
(, ) (, ) d,
p
tp ht e
∞
−τ
−∞
ϕ= ττ
∫
1
(, ) (, ) d .
2
j
p
j
ht t pe p
j
σ+ ∞
τ
σ− ∞
τ= ϕ
π
∫
(1.2.10)
В стационарном случае
(
)
(
)
,tp t p
ϕ
=
ϕ
−
.
Модель нелинейного динамического инерционного объекта стро-
ится в предположении, что нелинейность и инерционность объекта
можно разделить и представить объект в виде последовательной комби-
нации двух звеньев: нелинейного безынерционного и динамического
линейного. В одномерном случае, предполагая, что инерционное звено
стационарно, выход объекта
)(ty
связан с его входом
)(tx
одним из
двух соотношений:
()
0
() [ ( )]dyt h f xt
∞
=τ −ττ
∫
либо
0
() [ ()( )d].yt f h xt
∞
=
τ−ττ
∫
(1.2.11)
Задача идентификации будет состоять в определении пары функ-
ций
)(th
и
)(tf
.
2. Динамические системы, описываемые обыкновенными диффе-
ренциальными уравнениями. Модель линейного динамического объекта,
на вход которого поступает сигнал
)(tx
, вызывающий сигнал
)(ty
, час-
то представляют в виде обыкновенного дифференциального уравнения
10 10
dd dd
... ...
dd dd
nm
nm
nm
yy x x
aaaybbbx
tt tt
++ + = ++ +
, (1.2.12)
где
0
d(0)/d
iii
yty=
,
0,1,..., 1in=−
– начальные состояние системы; n и
m – параметры структуры (порядок) уравнения.
Если система нестационарная, то коэффициенты уравнения
i
a и
j
b
должны быть функциями времени. Задача идентификации заключается
в определении порядка уравнения, коэффициентов
ji
ba ,
и начальных
состояний (если они неизвестны).
Класс моделей на основе интегральных и обыкновенных диффе-
ренциальных уравнений имеет свои преимущества и недостатки. Моде-
ли на основе дифференциальных уравнений могут приводить к боль-
шим ошибкам идентификации, если порядок модели не соответствует
порядку объекта. Преимущество моделей на основе интегральных урав-
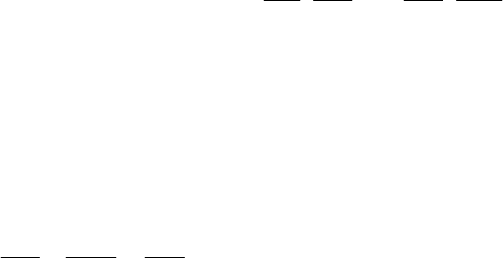
13
нений состоит в том, что они не требуют явного знания порядка объек-
та. Однако в этом случае описание объекта является непараметриче-
ским, бесконечномерным, поскольку определение функции эквивалент-
но определению (заданию) бесчисленного числа параметров.
3. Нелинейные динамические модели. В непрерывном случае одно-
мерный динамический объект (один вход и один выход) может быть
в
простейшем случае описан с помощью нелинейного дифференциально-
го уравнения
),...,,,...,()(
1
xxyyfty
mnn −
=
, (1.2.13)
где f – нелинейная функция
1
+
+
mn
аргумента, которую и нужно
идентифицировать.
4. Динамические системы, описываемые дифференциальными
уравнениями в частных производных. Динамические объекты, представ-
ленные дифференциальными уравнениями в частных производных,
имеют чрезвычайно широкое научное и практическое применение при
решении разнообразных задач гидротермодинамики, переноса излуче-
ния, прогноза погоды, динамики атмосферы и океана и т. д. [23].
Дифференциальное уравнение с частными
производными порядка
r есть функциональное уравнение вида
2
2
12 1
( , , , , ..., , , ...) 0
n
ff f f
FX f
xx x x
∂∂ ∂∂
=
∂∂ ∂ ∂
, (1.2.14)
содержащее по меньшей мере одну частную производную порядка r от
неизвестной функции
)( Xf
, где
),...,,(
21 n
xxxX
=
.
В качестве примера рассмотрим дифференциальное уравнение па-
раболического типа однофазной фильтрации, которое описывает плос-
корадиальный приток сжимаемой жидкости к скважине нефтяного пла-
ста
2
2
P
PP
rr rr t
∂∂ ∂
+=
∂∂χ∂
, где P – давление в момент времени t на расстоянии
r от оси скважины; χ – коэффициент пъезопроводности пласта, который
характеризует скорость перераспределения давления в пласте.
Задача идентификации заключается в определении пъезопроводно-
сти пласта по результатам гидродинамических исследований скважины
и регистрации кривой изменения давления после остановки скважины.
5. Дискретные, конечно-разностные аналоги интегральных
и диф-
ференциальных уравнений. При решении задач идентификации широкое
применение получили дискретные, конечно разностные аналоги инте-
гральных и дифференциальных уравнений с использованием численных
методов [23].

14
Суть этих методов заключается в замене интегралов суммами, а
производных их конечными разностями. Это позволяет свести инте-
гральные и дифференциальные уравнения к соответствующим системам
сеточных алгебраических уравнений.
Решение уравнений определяется в узлах сетки, что часто требует
запоминания большого объема данных и проведения больших вычисле-
ний.
1.3. Математические модели объектов-аналогов и априорной информации
Сведения об объектах идентификации условно можно разделить на
следующие типы:
1. Исходные и дополнительные данные (наблюдения входов и вы-
ходов объекта; дополнительные апостериорные и априорные данные).
2. Априорная информация о структуре модели объекта.
3. Априорная информация о статистических характеристиках слу-
чайных неконтролируемых переменных.
1. Исходные и дополнительные данные. Основным источником ис-
ходных
данных для идентификации являются результаты прямых на-
блюдений входных и выходных переменных объекта.
В качестве дополнительных апостериорных (текущих) данных мо-
гут быть использованы измерения, полученные из косвенных наблюде-
ний переменных объекта.
К априорной информации могут быть отнесены данные, получен-
ные на основе экспертных оценок переменных объекта, а также на ос-
нове
различных методик их расчета и т. д.
Удобной моделью дополнительных апостериорных либо априор-
ных данных является понятие объекта-аналога, т. е. системы, подобной
исследуемому объекту.
Объект-аналог определим как реально существующий либо вооб-
ражаемый упрощенный объект, отражающий основные черты иссле-
дуемой системы, особенности его строения и функционирования, пред-
ставляющий и
формализующий в виде моделей дополнительные апо-
стериорные и априорные данные, накопленный опыт и знания.
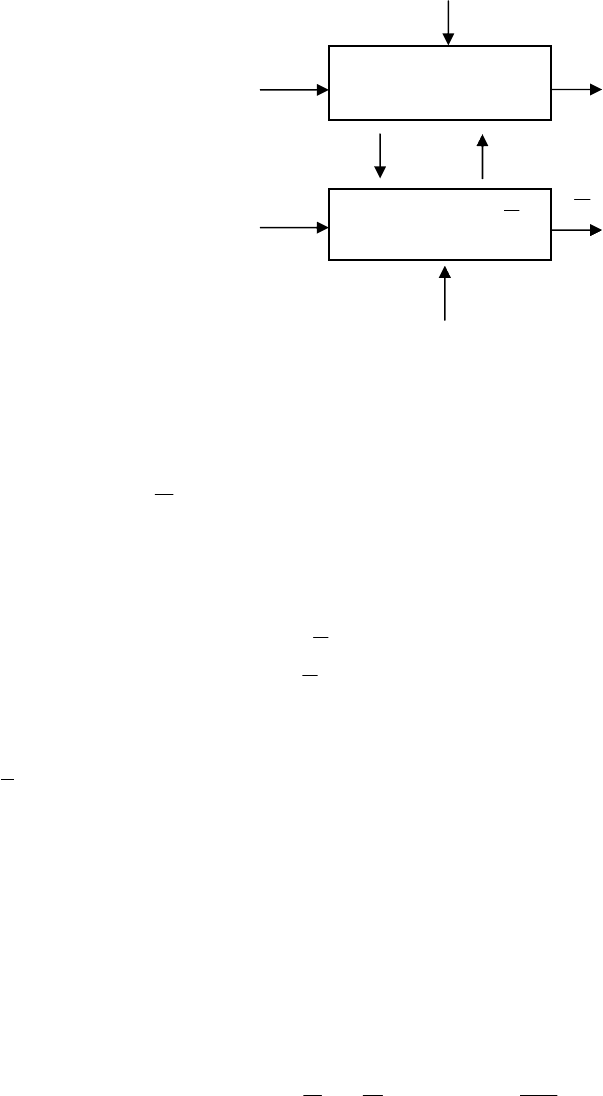
Объект-аналог
F
, изображенный на рис. 1.2, является некоторым
отражением исследуемого объекта F.
Исследуемый объект и объект-аналог представляют некоторую ин-
тегрированную систему взаимодействующих моделей первого уровня:
(,);
(,),
YFX
ZFZ
=
ξ
⎧
⎨
=
η
⎩
(1.3.1)
15
где η – случайные возмущения, связанные, например, с ошибками зада-
ния дополнительных априорных данных.
Рис. 1.2
Переменная Z объекта-аналога может соответствовать входным X
либо выходным Y переменным, а также представлять параметры, функ-
ции (функционалы), определяющие структуру исследуемого объекта.
Переменная
Z
представляет дополнительные апостериорные либо ап-
риорные данные.
Например, дополнительные априорные данные о параметрах моде-
ли нелинейного параметрического объекта (1.3.1) могут быть представ-
лены объектом-аналогом
η
=
+αα
, где η – случайные ошибки задания
дополнительных данных
α
.
Дополнительные априорные сведения о выходной переменной ис-
следуемого объекта могут быть также представлены объектом-аналогом
() ηygy=+, где g – некоторая неизвестная функция регрессии.
Как и для исследуемых объектов операторы и математические моде-
ли объектов-аналогов могут быть представлены математическими зависи-
мостями (1.2.2)–(1.2.14). Объекты-аналоги также могут быть статическими
либо динамическими, линейными либо нелинейными системами.
Исследуемой системе может соответствовать не один, а несколько
объектов-аналогов. В этом случае интегрированная система первого
уровня имеет вид
⎪
⎩
⎪
⎨
⎧
==
=
.,1),η,(
),ξ,(
mjZFZ
XFY
j
jj
(1.3.2)
На основе интегрированной системы (1.3.2) могут быть представ-
лены, например, исходные и дополнительные данные о параметрах и
выходе нелинейного параметрического статического объекта в виде
Объект-аналог
F
Исследуемый
объект
F
ξ
X
Y
Z
Z
η

16
единой интегрированной стохастической системы взаимодействующих
моделей:
(, ) ξ,
ααη,1,,
() , 1,.
jjj
iii
f
j
m
ygy i n
ν
⎧
=+
⎪
⎪
=+ =
⎨
⎪
=+=
⎪
⎩
yxα
(1.3.3)
Объекты-аналоги
Z
в свою очередь могут быть использованы в ка-
честве исходных исследуемых систем и иметь свои аналоги –
Z
. Тогда
имеем интегрированную стохастическую систему второго уровня
⎪
⎪
⎩
⎪
⎪
⎨
⎧
==
==
=
.,1),η,,(
,,1),η,(
),ξ,(
lkZZFZ
mjZFZ
XFY
jkj
jjkjk
jj
jj
(1.3.4)
В общем случае интегрированная система моделей может иметь
неограниченное число уровней и представляет некоторую иерархиче-
скую структуру.
2. Априорная информация о структуре объекта. Априорная ин-
формация о структуре объекта известна еще до наблюдений входов и
выходов объекта и носит в основном качественных характер и позволя-
ет выбрать модель объекта и определить
его структуру.
3. Априорная информация о статистических характеристиках слу-
чайных неконтролируемых переменных. Основная трудность идентифи-
кации систем состоит в том, что в большинстве реальных ситуаций на-
блюдения над исследуемыми объектами и объектами-аналогами искаже-
ны случайными возмущениями, которые определяются многими причи-
нами. Погрешности могут появляться за счет ошибок регистрации вход-
ных
и выходных переменных объекта, ошибок выбора структуры модели
объекта, ошибок задания дополнительной априорной информации и т. д.
Обычно эти ошибки описываются с помощью аддитивных помех.
Наличие помех, искажающих наблюдаемые входные и выходные
сигналы, приводит к тому, что для идентификации должны использо-
ваться статистические методы.
Плотности распределения вероятностей помех с формальной
точки
зрения могут быть любыми. Однако на практике часто возникают ти-
пичные ситуации, связанные с одинаковым механизмом их возникнове-
ния. Важную роль играют законы распределения вероятностей помех:
равномерный закон, нормальный закон, закон Лапласа.

17
1.4. Интегрированные системы моделей и их классификация
Под интегрированной системой моделей (рис. 1.3) будем понимать
совокупность модели исследуемого объекта и модели объектов-
аналогов.
Рис. 1.3
Введем следующую классификацию интегрированных систем мо-
делей (ИСМ):
1. Линейные ИСМ:
• линейные статические ИСМ;
• линейные динамические ИСМ.
2. Нелинейные ИСМ:
• нелинейные статические ИСМ;
• нелинейные динамические ИСМ.
3. Линейные непараметрические ИСМ:
• линейные непараметрические статические ИСМ;
• линейные непараметрические динамические ИСМ.
4. Нелинейные непараметрические ИСМ:
• нелинейные непараметрические статические ИСМ;
• нелинейные непараметрические динамические ИСМ.
5. Непараметрические ИСМ:
• статические непараметрические ИСМ;
• динамические непараметрические ИСМ.
Приведем примеры стохастических интегрированных систем моде-
лей, основанных на стохастических моделях исходных объектов и сто-
хастических моделях объектов-аналогов.
1. Линейные интегрированные системы моделей. Линейные интег-
рированные системы моделей основаны на линейных статических либо
динамических моделях исследуемых объектов и на линейных (статиче-
ских либо динамических) моделях объектов-аналогов.
В качестве при-
мера линейной статической интегрированной системы моделей первого
уровня рассмотрим регрессионную модель объекта и модель дополни-
тельной априорной информации вида:
Интегрированная система моделей
Модель объекта Модели аналогов
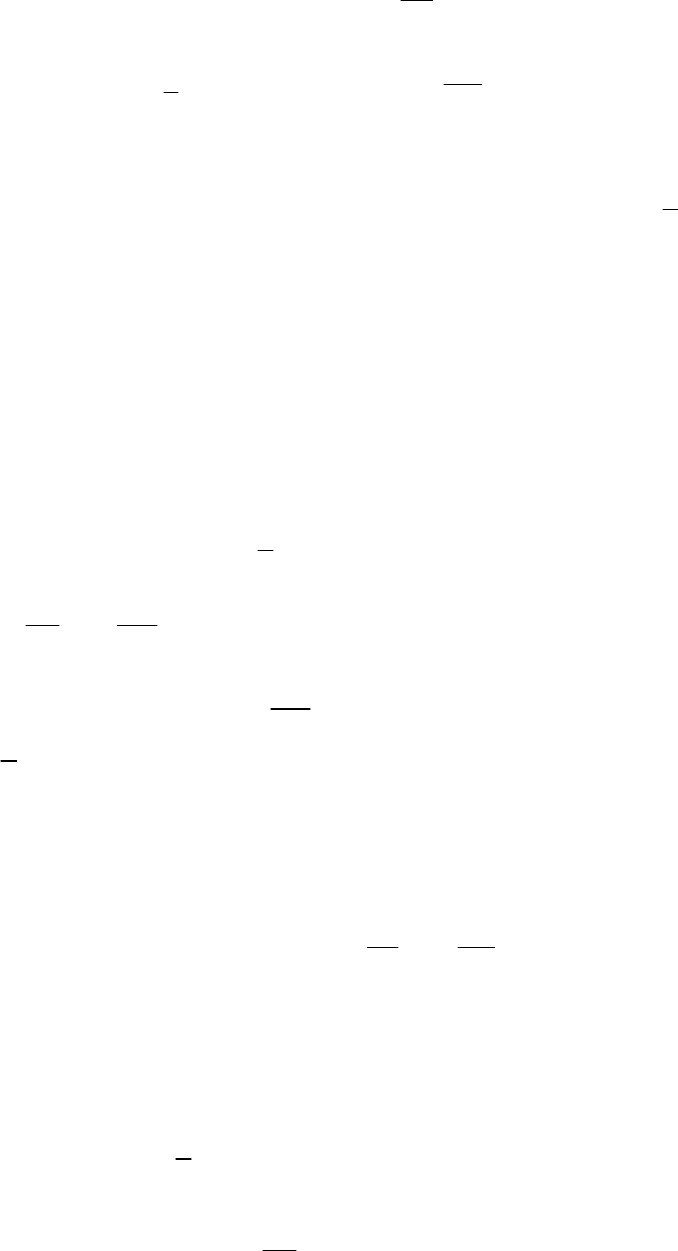
18
*
1
1
,1,;
,, 1,,
m
iijji
j
m
jjkkj
k
yx in
rjkm
=
=
⎧
=α+ξ=
⎪
⎪
⎨
⎪
α= α+η =
⎪
⎩
∑
∑
(1.4.1)
где
*
i
y
– измеренные значения выхода объекта
y
;
j
x
– входные пере-
менные объекта;
j
α
– неизвестные параметры модели объекта;
j
α
– до-
полнительные априорные данные о параметрах объекта, являющиеся в
свою очередь выходными переменными объекта-аналога;
jk
r
– некото-
рые известные параметры объекта-аналога;
ij
x
– значения входных пе-
ременных;
i
ξ
– ошибки измерения выхода объекта,
j
η
– ошибки зада-
ния априорной информации.
Модель (1.4.1) удобно представить в матричной форме
*
;
,
⎧
=
+
⎨
=
+
⎩
yFα
ξ
α Rα
η
(1.4.5)
где
F – матрица, которую часто называют матрицей планирования
(, 1,, 1,);
ij
x
injm===F
*
,,y αξ
имеют смысл векторов измерений вы-
хода объекта, параметров модели и ошибок измерений выходной пере-
менной объекта;
(,, 1,)
jk
rjk m==R
– матрица коэффициентов объекта-
аналога;
,αη
– векторы дополнительных априорных данных и ошибок
их задания.
Линейной считается интегрированная система моделей, в которой в
качестве входных переменных (регрессоров) объекта используются их
функциональные преобразования вида
()
j
f x
. В данном случае, матрица
планирования имеет вид
((), 1,, 1,)
jij
f
xi nj m===F
.
В качестве примера линейной динамической интегрированной сис-
темы моделей первого уровня приведем уравнения:
*
0
()( ) ;
,1,,
T
iii
iii
yhxtd
hh i n
⎧
=τ −ττ+ξ
⎪
⎨
⎪
=+η=
⎩
∫
(1.4.6)
где априорная информация об ИПФ
(τ)h
задана в моменты измерения
выхода объекта
**
(), 1,
ii
yyti n==
.
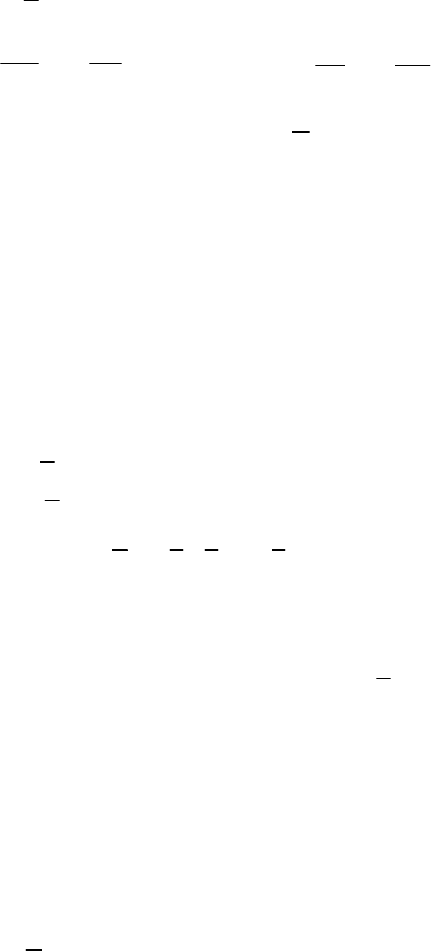
19
Используя представление ИПФ в виде ряда известных функций
)(α)(
1
tfth
j
m
j
j
∑
=
=
, интегрированная система моделей (1.4.6) сводится к
линейной статистической системе вида
*
;
,
t
⎧
=
+
⎪
⎨
=
+
⎪
⎩
yFα
ξ
hHαη
, (1.4.7)
где
0
(()( )d, 1,,1,)
T
ji
f
xt jmin=τ−ττ= =
∫
F
; ((), 1,, 1,)
ji
f
Ti nj m===H – мат-
рица известных функций, вычисленных в точках
i
t
;
h
– вектор-столбец
дополнительных априорных данных о значениях ИПФ в моменты вре-
мени
i
t
.
В качестве примера рассмотрим линейную интегрированную сис-
тему моделей первого уровня с двумя объектами-аналогами, которые
дают возможность учитывать дополнительную априорную информацию
о параметрах модели исследуемого объекта и априорную информацию о
выходе
*
1
2
;
;
,
⎧
=+
⎪
=
+
⎨
⎪
=
+
⎩
yFαξ
Γα Rαη
Γ yHyν
(1.4.8)
где
F
,
R
,
H
– известные матрицы;
T
n
yyy ),...,,(
21
=y
– вектор допол-
нительных априорных данных о выходе объекта в моменты времени
i
t ,
заданный с ошибками
T
n
),...,,(
21
ννν
=ν
;
1
Γ
,
2
Γ
– диагональные (инди-
каторные) матрицы нулей либо единиц (где, например,
0
j
×α
означает,
что априорная информация о
j компоненте вектора α отсутствует).
При
1
(1,0,0,...,0)=Г
,
2
(0,0,..., 0)
=
Г
,
I
=
=RH
, интегрированная
система моделей (1.4.8) переходит в интегрированную систему с одним
объектом-аналогом, который представляет дополнительную информа-
цию только о первой компоненте вектора параметров
α:
*
111
,
.
⎧
=
+
⎨
α
=α +η
⎩
yFα
ξ
2. Нелинейные интегрированные системы моделей. Нелинейные
интегрированные системы моделей основаны на нелинейных статиче-
ских либо динамических моделях исследуемых объектов и линейных
либо нелинейных моделях объектов-аналогов.
20
В качестве примера рассмотрим нелинейную статическую интегри-
рованную систему моделей, в которой линейная модель объекта-аналога
представляет дополнительную априорную информацию о неизвестных
параметрах модели исследуемого объекта:
*
(,) , 1,,
α ,
iii i i
yy f
in
ξξ
η
⎧
=+= + =
⎪
⎨
=⋅+
⎪
⎩
x α
R α
(1.4.9)
где
niy
i
,1,
*
=
– измеренные с ошибками
,,1,ξ ni
i
=
значения выхода объ-
екта
y;
),( αx
ii
fy =
– значения выхода модели объекта, полученные при
соответствующих значениях входов
),...,(
21 miiii
xxx
=
x
; ,,ηα R – опреде-
ленные в (1.4.5) характеристики объекта-аналога.
Рассмотрим пример нелинейной динамической интегрированной
системы моделей, в которой модель исследуемого объекта представлена
конечно-разностным аналогом нелинейного дифференциального урав-
нения первого порядка
d
(,,,)
d
tt
y
fyt
t
= α x
,
0
α)0(
=
y
, (1.4.10)
где
),,,(
tt
tyf xα
– нелинейная, относительно параметров
α
, функция;
0
α
– начальное значение.
При известной априорной информации о параметрах модели и вы-
ходе объекта имеет место нелинейная динамическая интегрированная
система моделей:
*
1
1
2
'( , , , , ) , 1, , (0) (0);
;
,
ttt tt t t
yy fyyt t ny y
−
⎧
=+ξ= +ξ= =
⎪
=+
⎨
⎪
=+
⎩
α x
Гα Rαη
Г yHyν
(1.4.11)
где
*
t
y
– измеренное в моменты времени t значение выхода объекта y
t
;
),,,,('
1 ttt
tyyf xα
−
– конечно-разностная аппроксимация модели объекта,
),...,,(
21 mtttt
xxx=x
– заданные значения входных переменных объекта.
В общем случае для нелинейного дифференциального уравнения и
s объектов-аналогов, динамическая нелинейная интегрированная сис-
тема моделей примет вид:
*
12
12
1
1
2
212
(, ,,,, , 1,, 1,);
(), ( ),1,, 1,;
,1,;
,1,, ,
tttittj
ti t j
kk k
k
lll
l
yFyyt i rj r
y yti tjirjr
ks
lssss
−−
−−
⎧
===
⎪
=− =− = =
⎪
⎨
=+ =
⎪
⎪
=+= =+
⎩
α xx
xx
Гα R αη
Г yHyν
(1.4.12)
