Сергеев В.Л. Интегрированные системы идентификации
Подождите немного. Документ загружается.


41
Для этой цели необходимо вычислить производные от функционала
Ф(Δα
0
) по параметрам Δα
0
и приравнять их к нулю
0
0
0000
0
0
0
0
()
()2 ( )
2( )0.
T
y
T
α
α
Δ
∂Δ
=∇ Δ =− − Δ −
Δ
−Δ−Δ=
Φα
Φα DW e D α
α
RW α R α
(3.1.7)
В результате получим систему линейных уравнений
111
)β()β(
−−−
Δ⋅+=Δ⋅+
iT
y
TiiT
y
T
αWReWDαRWRDWD
αα
, (3.1.8)
относительно приращений вектора параметров
1
−
Δ
i
α
на шаге 1,i
−
1, 2, 3, ...i = Индекс
1−i
означает, что все переменные системы линей-
ных уравнений вычислены при значениях
1
, 1, 2, 3, ...
i
i
−
=
=αα
Для обеспечения сходимости процедуры определения параметров
(3.1.6), (3.1.8), необходимо выполнение условия
1
() ( )
ii
−
<Φα Φα , 1, 1, 2, 3, ...ii
−
= (3.1.9)
на каждом шаге итерационного процесса.
Для этой цели существует ряд методов, приведенных в приложении 3.
В методе Гаусса–Ньютона выполнение условия сходимости (3.1.9) осу-
ществляется дроблением шага ( 1, 1, 2, 3, ...)
i
hh i
=
∀= пополам
1
/ 2 , 1, 2, 3, ...
i
i
hh i
−
==.
Рассмотрим интегрированную систему моделей, в которой априор-
ная информация о параметрах модели объекта представлена системой
нелинейных уравнений
⎪
⎩
⎪
⎨
⎧
+=
+=
,)(
,),(
*
ηαα
ξαxfy
r
(3.1.10)
где r(
α) – вектор нелинейных функций
12
( ( ), ( ), ..., ( ))
T
m
rr rαα α
.
Используя разложение функции
),( αxf
и
)(αr
в ряд Тейлора вида
(3.1.3), перейдем к линейной, относительно параметров
0
αΔ
, интегри-
рованной системе моделей вида:
⎪
⎩
⎪
⎨
⎧
+Δ=
+Δ=
,
,
000
000
ηαDe
ξαDe
rr
ff
(3.1.11)
где
0
0
,1, ,
)(
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∂
∂
= mji
r
j
i
r
α
α
D
– квадратная матрица частных производных
функции r(
α) по параметрам α,
),,(
0*0
αxfye −=
f
),(
00
ααe r
r
−=
а
00
, αD Δ
f
–
определены в (3.1.3).
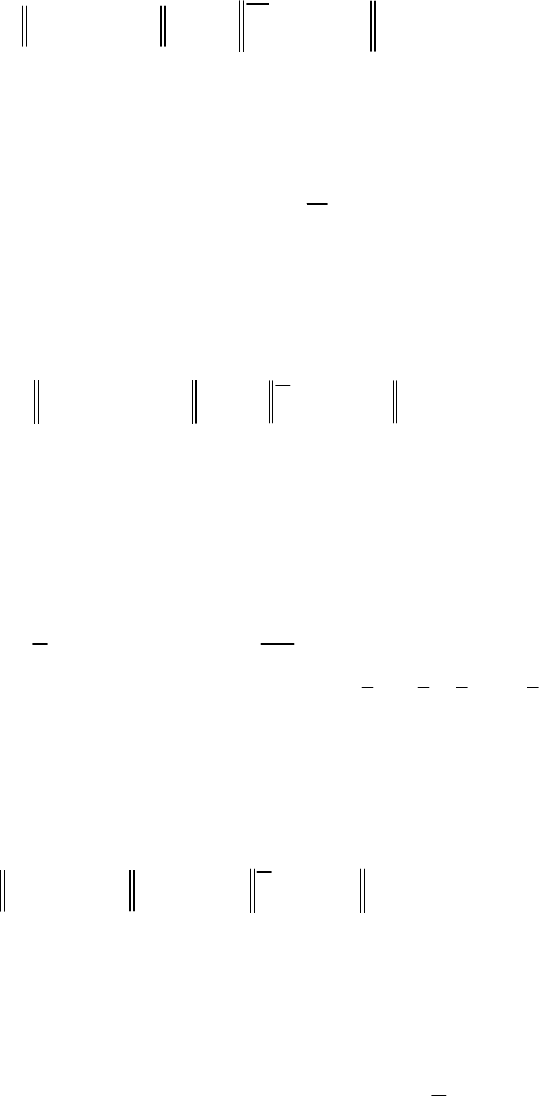
42
Для интегрированной системы моделей (3.1.11) по аналогии с
(3.1.5) имеет место комбинированный критерий качества
2
2
0000 000
() β .
ff rr
W
W
Δ=−Δ +⋅−Δ
y
α
Φα eDα eDα
(3.1.12)
В данном случае алгоритм адаптации с использованием метода
Гаусса–Ньютона по аналогии с (3.1.6), (3.1.8) сводится к итерационной
процедуре вида:
11
11 0 01
,
( β )( β ), 1,2,3,....
ii i
i
TTiiTTi
yrr yrr
ff ff
h
i
−−
−− −
⎧
⎪
⎨
⎪
⎩
=+Δ
+⋅ Δ = +⋅ =
αα
αα α
DWD DWD α DWe DWe
(3.1.13)
Важным моментов в алгоритмах адаптации (3.1.6) и (3.1.13) являет-
ся определение управляющего параметра, который (в упрощенном ва-
рианте) может быть определен на первом шаге итерационного процесса
путем решения оптимизационной задачи вида
2
2
**1 1
β
β arg min( ( , (β) β (β).
W
W
=− +⋅−
α
y
yfxααRα
Полученное значение управляющего параметра β
*
может быть исполь-
зовано на последующих шагах.
Рассмотрим интегрированную систему моделей, в которой априор-
ная информация о параметрах модели объекта формируется на основе
использования l объектов-аналогов:
*
(, ) ,
, 1, ,
k
kk
kl
⎧
=
+
⎪
⎨
=+ =
⎪
⎩
yfxαξ
α R αη
(3.1.14)
где
R
k
– известная матрица для k объекта-аналога;
12
(
α ,α ,..., α )
kkkmk
=
α –
вектор дополнительных априорных данных для k объекта-аналога.
Поставим в соответствие данной интегрированной системе моделей
квадратичный функционал качества, предполагая, что случайные вели-
чины
ξ и η распределены по нормальному закону
2
1
2
*
β),()(
α
y
W
W
αRααxfyαΦ
k
k
l
k
k
−+−=
∑
=
. (3.1.15)
Тогда алгоритм определения параметров
α при использовании ме-
тода Гаусса–Ньютона по аналогии с (3.1.6), (3.1.8) сводится к рекур-
рентной процедуре
11
11 1
11
, 1, 2, 3, ...
( β )( β ).
ii i
j
ll
TTiiTTi
k
y
kk kk k k k
kk
hi
−−
−− −
==
⎧
⎪
⎪
⎨
⎪
⎪
⎩
=+Δ =
+Δ=+Δ
∑∑
y
αα
αα α
DWD RW R α DWe RW α
(3.1.16)
Алгоритм адаптации, основанный на методе Ньютона–Рафсона.
Для решения оптимизационной задачи часто используется метод Нью-
тона, приведенный в приложении 2, основанный на использовании вто-

43
рых частных производных при разложении функционала качества
)(αΦ
в ряд Тейлора в окрестности точки α
0
000000
)())(()()( αHαααΦαΦαΦ
α
Δ
Δ
+
Δ
∇
+=
T
, (3.1.17)
где H
0
– матрица Гессе вторых частных производных с элементами
02
),1,/)(( mi,
j
ji
=α∂α∂∂ αΦ
,
)(
00
ααα
−
=
Δ
, а индекс «0» означает, что
частные производные вычислены при
0
=
αα
.
Необходимым условием минимума функционала (3.1.17) является
равенство нулю частных производных по
0
α
Δ
0
000
)( ()) 0,
Δ
∇=∇ +Δ=
α
α
Φ(αΦαH α
(3.1.18)
где
00 0
(())( β )
TT
y
f
∇=∇⋅+⋅Δ
αα α
Φα fWe RW α
,
02 0
(
T
y
f
=
∇⋅ +∇⋅∇+
ααα
HfWeff
0
β )
T
+⋅
α
RWR
,
(()/α , 1, )
i
im∇=∂ ∂ =
α
ffα
,
22
(()/αα, 1, )
ij
i, j m
∇
=∂ ∂ ∂ =
α
ffα
,
0* 0
(, ),
f
=−eyfxα
0
Δ
=−ααRα
.
Процесс определения параметров α в данном случае проводится по
схеме:
11
20 11
01
,
( β )
( β ).
ii i
i
TTii
yy
f
TTi
y
f
h
−−
−−
−
⎧
⎪
⎪
⎨
⎪
⎪
⎩
=+Δ
∇⋅ +∇⋅ ∇+⋅ Δ =
=∇ ⋅ +⋅ Δ
αααα
αα
αα α
fWe fW f RWR α
fWe RW α
(3.1.19)
Преимуществом метода Ньютона–Рафсона (3.1.19) по сравнению с
методом Гаусса–Ньютона является то, что он обеспечивает более высо-
кую скорость сходимости. Недостатком является трудоемкость при вы-
числении матрицы вторых производных
2
.
∇
α
f
Следует отметить, что в последнее время широкое практическое
применение получили квазиньютоновские методы оптимизации (мето-
ды переменной метрики), приведенные в приложении 2, позволяющие
строить различные аппроксимации матрицы Гессе.
3.2. Нелинейные интегрированные системы идентификации
с учетом априорной информации о выходе объекта
Рассмотрим интегрированную систему моделей, основанную на не-
линейной статической стохастической модели объекта и нелинейной
модели дополнительной априорной информации о его выходе
*
(, ) ,
() ,
⎧
⎪
⎨
⎪
⎩
=
+
=
+
yfxαξ
ГyLy η
(3.2.1)
где L – известный оператор (функция, функционал и т. д.); y
*
– векторы
измеренных значений выхода объекта;
y
– дополнительные априорные
данные, полученные с «объекта-аналога»; ( , )fxα – вектор нелинейной
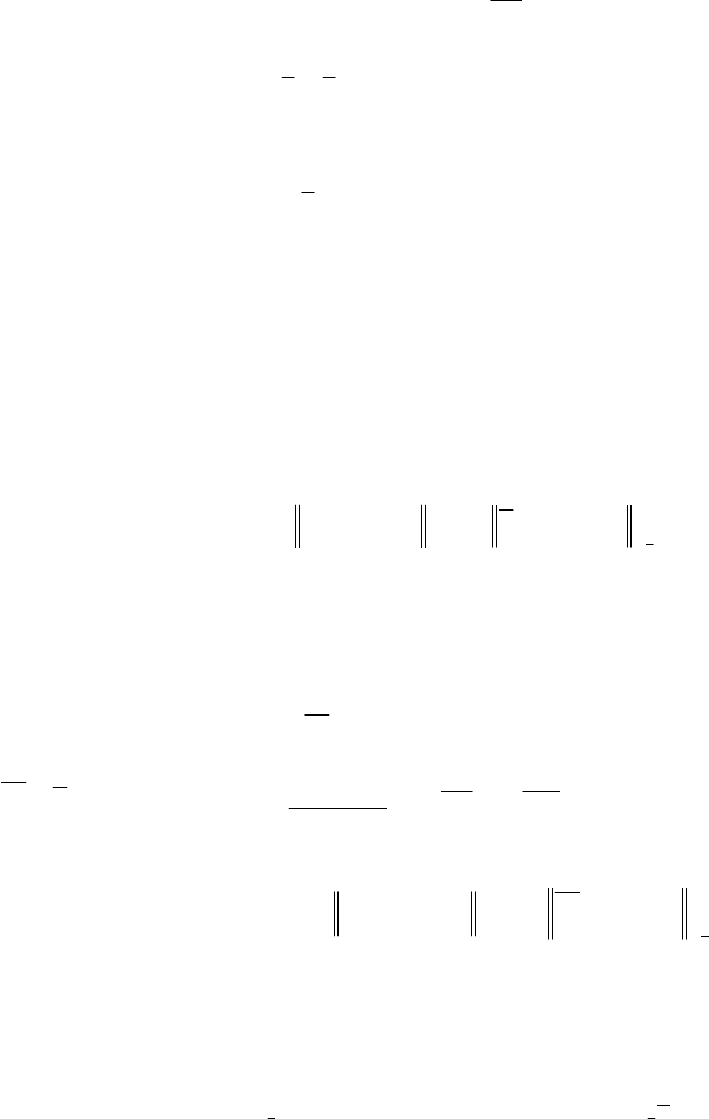
44
функции ,)
f
( x α вычисленной в точках ,1,
i
in
=
x ;,
ξ
η – векторы случай-
ных величин; L – диагональная индикаторная матрица.
Введем обозначения
, ( , )
Г
=
=L
yy
L
yg
x α , с учетом которых интег-
рированную систему моделей (3.2.1) представим в виде:
*
(, ) ,
(, ) .
Г
⎧
⎪
⎨
⎪
⎩
=
+
=
+
yfxα
ξ
ygxαη
(3.2.2)
Алгоритм адаптации, основанный на методе Гаусса–Ньютона.
Используя прием разложения нелинейных функций (, )
f
x α и (, )g x α
в ряд Тейлора с точностью до членов первого порядка малости:
000
α
00
α
0
(, ) (, ) (, ) ,
(, ) (, ) (, ) ,
T
T
ff f
gg g
=+∇ Δ
=+∇ Δ
x α x α x αα
x α x α x αα
(3.2.3)
приведем решение оптимизационной задачи
*
2
2
*
(β)argmin()
() β () (,) β (, )
y
Г
W
W
=
=
=+ =− + −
y
α
αΦα
J α Q α yfxα ygxα
(3.2.4)
с использованием итерационной процедуры Гаусса–Ньютона по анало-
гии с алгоритмом адаптации (3.1.13). Для этой цели линеаризуем интег-
рированную систему (3.2.2)
000
000
,
,
ff
gg
⎧
⎪
⎨
⎪
⎩
=
Δ+
=
Δ+
eDα
ξ
eDαη
где
00
(, )
g
Г
=−eygxα ,
0
0
(,)
, 1, , 1,
α
i
g
j
g
injm
⎛⎞
⎜⎟
⎜⎟
⎝⎠
∂
===
∂
x α
D
и перейдем к ре-
шению оптимизационной задачи
2
2
*0000000
arg min( ( ) β
y
gg
ff
W
W
Δ
Δ= Δ = − Δ +⋅ − Δ
y
α
αΦαeDα eDα
для определения оптимального вектора приращений параметров
0
Δα .
В данном случае процедура уточнения параметров (по аналогии с про-
цедурой (3.1.13)) имеет вид:
11
11 1
,
( β )( β ),
1, 2, 3, ... .
ii i
i
TTiiTTi
ygyq ygyg
ff ff
h
i
−−
−− −
⎧
⎪
⎪
⎨
⎪
⎪
⎩
=+Δ
+⋅ Δ = +⋅
=
αα α
DWD DWD α DWe DWe
(3.2.5)
Для получения (3.2.5) достаточно взять производные от функцио-
нала
0
(ΔΦα) по параметрам
0
Δ
α и приравнять их к нулю.
Для интегрированной системы моделей, в которой априорная ин-
формация о выходе объекта получена с l объектов-аналогов

45
*
(, ) ,
(, ) , 1,,
Гk
kk
kl
⎧
⎪
⎨
⎪
⎩
=+
=+=
yfxαξ
ygxαη
(3.2.6)
процедура уточнения параметров (по аналогии с (3.2.5)) примет вид
11
11
k
1
1
k
1
,
( β )
( β ) , 1, 2, 3, ... .
ii i
i
l
TTii
y
ff gk gk
yk
k
l
TTi
y
f f gk gk
yk
k
h
i
−−
−−
=
−
=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
=+Δ
+⋅ Δ=
=+⋅ =
∑
∑
αα α
DWD D W D α
DWe D We
(3.2.7)
На основе приведенных в приложении 2 методов оптимизации
функций для интегрированной системы моделей (3.2.2) и (3.2.6) можно
получить различные процедуры адаптации вектора неизвестных пара-
метров α. Например, для интегрированной системы моделей (3.2.2) ме-
тод Ньютона–Рафсона (по аналогии с алгоритмом (3.1.19)) приводит к
итерационной процедуре вида
11
20 11
01
,
( β )
( β ).
g
ii i
i
TTii
yygg
f
TTi
yg
f
y
h
−−
−−
−
⎧
⎪
⎪
⎨
⎪
⎪
⎩
=+Δ
∇⋅ +∇⋅ ∇+⋅ Δ =
=∇ ⋅ +⋅
αααα
α
αα α
fWe fW f DWD α
fWe DWe
(3.2.8)
3.3. Нелинейные комбинированные интегрированные
системы идентификации
Рассмотрим интегрированную систему моделей, основанную на не-
линейной статической стохастической модели объекта и моделей объек-
тов-аналогов, дающих дополнительную априорную информацию о па-
раметрах и выходной переменной модели. Рассмотрим также класс объ-
ектов-аналогов, представляющий дополнительную априорную инфор-
мацию о выходе объекта в интегральном виде. Остановимся на интег-
рированной системе моделей
вида:
*
1
2
33
(, ) ,
() ,
,) ,
(, ) () ,
m
R
sz d s
η
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
=+
=+
=+
=+=+
∫
yfxαξ
α r αη
yg(xαη
x α x αη
(3.3.9)
где (,), (), (,),(,)
f
ff zx ααx α x α – известные нелинейные функции (в об-
щем виде функционалы);
*
,,y α
y
– соответственно, векторы измерен-
ных значений выхода объекта и априорных дополнительных данных о
параметрах модели объекта и его выходе;
s
– дополнительная априор-
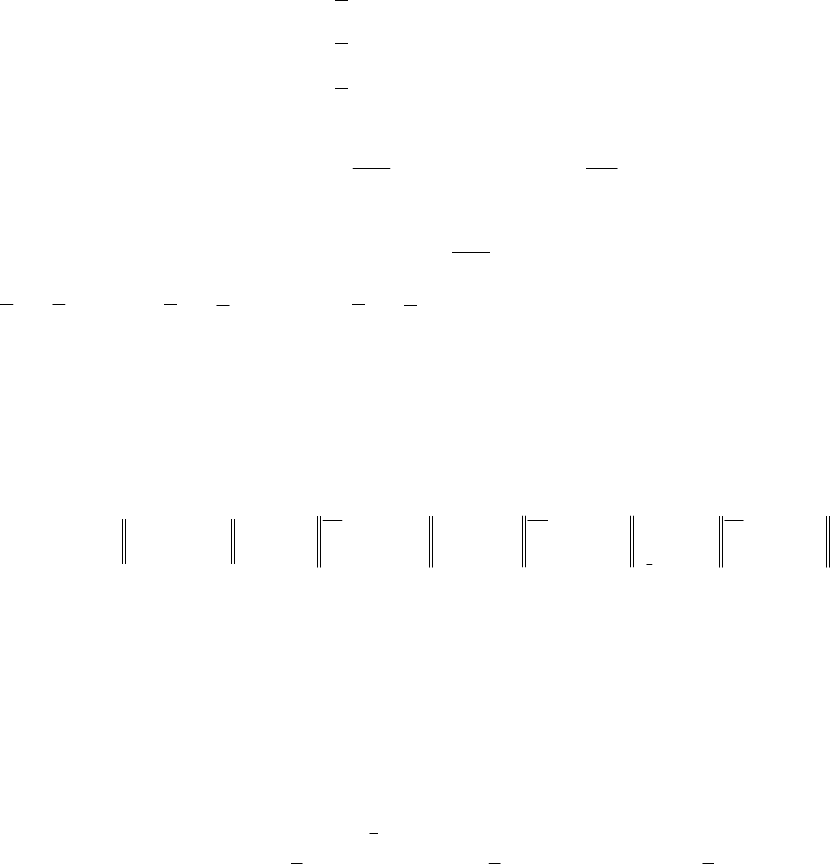
46
ная информация о выходе объекта, заданная в интегральной форме;
123
,, ,ξη η η – векторы случайных величин.
От интегрированной системы моделей (3.3.9) перейдем к линеари-
зованной интегрированной системе моделей относительно приращений
Δα
0
, где все нелинейные функции представлены рядом Тейлора в окре-
стности точки α
0
с точностью до членов первого порядка малости:
000
000
1
000
2
000
3
,
,
,
,
ff
rr
gg
ss
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
=
⋅Δ +
=⋅Δ+
=⋅Δ+
=⋅Δ+
eDα
ξ
eDαη
eD αη
eDαη
(3.3.10)
где
00
,
g
f
DD – матрицы частных производных от функций f, g соответст-
венно по параметрам
α , 1,
j
j
m
=
в точках ,1,
i
in
=
x при начальных зна-
чениях α = α
0
;
00
,
rs
DD – векторы частных производных от функции r и
функционала
s по параметрам α , 1,
j
j
m
=
;
0* 0
(, )
f
=
−eyfxα ;
00
()
r
=−e α r α
;
00
(, )
g
=
−eygxα ;
00
()
s
ss
=
−e α
.
Интегрированной системе моделей (3.3.10) поставим в соответст-
вие комбинированный взвешенный критерий качества, основанный на
частных квадратичных функционалах качества:
3
00 0
1
()() ()
jj
j
β
=
Δ=Δ+ Δ
∑
Φα J α Q α
, (3.3.11)
где
2
000
()
y
f
W
Δ= −ΔJ α eDα ;
2
000
1
rr
W
α
=−ΔQeDα ;
2
000
2
y
gr
W
=−ΔQeDα
;
2
000
3
s
ss
W
=−ΔQeDα .
В качестве оптимальных значений Δα
*
приращения параметров Δα
0
используем величину
*0
arg min ( ).Δ= Δ
0
Δα
αΦα (3.3.12)
Для решения задачи (3.3.12) достаточно вычислить производные от
0
()ΔΦαдо
0
Δα и приравнять их к нулю
00 00
00 00
()2 2
220,
yrr
ff
zg sss
y
α
Δ=− − −
−−=
Φα DWE DWE
DWE DWE
(3.3.13)
где
000
()
fff
=−ΔEeDα ;
000
()
rrr
=−ΔEeDα ,
00 0
()
ggg
=
−⋅ΔEeDα ,
000
()
sss
=
−ΔEeDα .
Собирая члены c
0
Δα из (3.3.13), получим систему линейных урав-
нений, которую запишем для произвольного вектора приращений
1i
−
Δα
на шаге
i – 1, начиная с
0
, 1,2,3...iΔ=α ,
11 1ii i
−
−−
Δ
=A α B , (3.3.14)
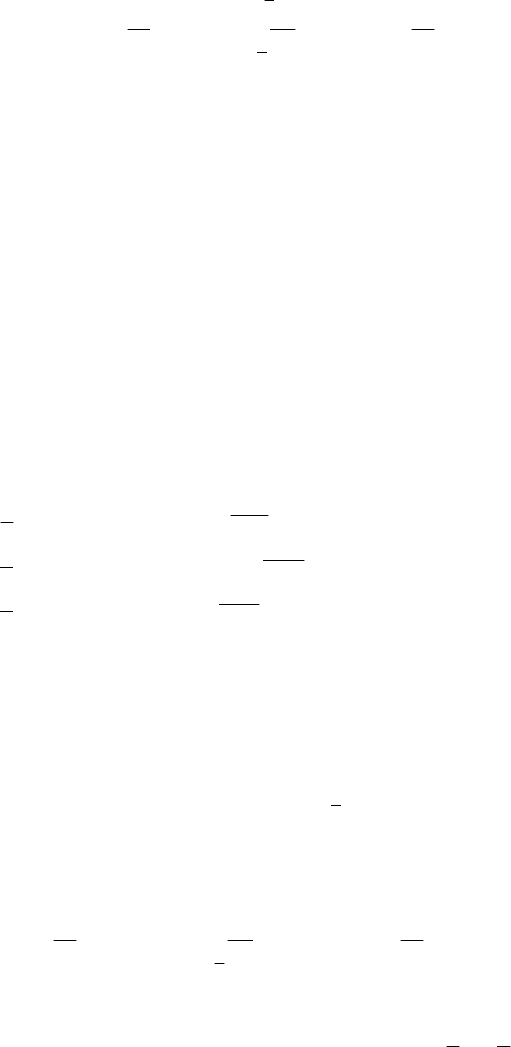
47
где
1 1
123
10 0 0 01
123
( ββ β)
( ββ β),
iTTTTTi
yrrggsss
ff
y
iT T T Ti
yrrzgsss
f
y
α
α
− −
− −
=+ + +
=+ + +
A D WD D WD D WD D WD
B DWe DWe DWe DWe
индекс
1−i
означает, что все переменные вычислены при
1i−
=αα
.
Основываясь на схеме Ньютона с учетом (3.3.13), процедура уточ-
нения параметров α примет вид
11
11 1
,
, 1, 2, 3, ... .
ii i
i
ii i
h
i
−−
−− −
⎧
⎪
⎨
⎪
⎩
=+Δ
Δ= =
αα α
A α B
(3.3.15)
Отметим, что при значениях управляющих параметров
123
β = β = β = 0
и
y
=WI, алгоритм определения параметров (3.3.14)
совпадает с методом Гаусса–Ньютона для идентификации модели
объекта (, ).
f
x α
Для интегрированной системы моделей вида:
*
1
1
2
2
3
3
(, ) ,
() , 1,,
(, ) , 1, ,
() , 1, ,
kk k
kk k
kk
f
rkl
kl
ss k l
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
=+
=+ =
=+=
=+ =
yxαξ
ααη
ygxαη
αη
, (3.3.16)
в которой дополнительная априорная информация получена c
123
lll++
объектов-аналогов, процедура уточнения параметров проводится по
схеме, аналогичной (3.3.14), где
12
3
3
12
1
2
1
11
1
3
1
10 0 0 01
123
11 1
( ββ
β )
( ββ β).
ll
iTT T T
ygg
ff krkkrk
y
kk
l
Ti
sss
k
l
ll
iT T T Ti
yrrzgsss
f
y
kk k
α
α
−
==
−
=
− −
== =
=+ + +
+
=+ + +
∑∑
∑
∑∑∑
ADWD DWD DWD
DWD
B DWe DWe DWe DWe
(3.3.17)
Следует отметить, что дополнительные априорные данные могут
быть известны только по некоторым компонентам векторов
α и
y
.
3.4. Нелинейные динамические интегрированные системы идентификации
Нелинейные динамические интегрированные системы идентифика-
ции рассмотрим на примере нелинейной динамической интегрирован-
ной системы моделей вида:
48
*
( ) , (0) (0),
,
,
tt t
Fyy
⎧
⎪
⎪
⎨
⎪
⎪
⎩
=+ =
=+
=+
y αξ
α Rαη
yHyν
(3.4.1)
где
*
t
y
– вектор измеренных в моменты времени t значений выхода объ-
екта
t
y
1
() ( ( , ,, , ), 1,)
ttt
t
f
yyt t n
−
==F ααx – вектор функция, полученная в
результате конечно-разностной аппроксимации нелинейного дифферен-
циального уравнения первого порядка (1.4.10);
12
( , , ..., )
tmt
tt
x
xx
=
x
– зна-
чения входных переменных объекта в момент времени t, α – вектор не-
известных параметров;
R,H
– известные матрицы; , ,
t
ξ
ην – векторы
ошибок измерений выхода исследуемого объекта и ошибок задания ап-
риорной информации соответственно.
Представим в (3.4.1) функцию ()
t
F α рядом Тейлора в окрестности
точки
0
α с точностью до членов первого порядка малости. В результате
получим линеаризованную интегрированную систему моделей относи-
тельно приращений Δα
0
,
000
1
0
1
000
2
,
,
,
⎧
⎪
⎪
⎨
⎪
⎪
⎩
=
Δ+
Δ
=Δ+
=
Δ+
eDα
ξ
α R αη
eDα v
(3.4.2)
0010 0 000
121
1
,(α ,1,), (), ,
m
T
t
ij j
j
rim
=
Δ=− ⋅ = ⋅ = =− =
∑
ααRα R α e
y
HF α DHD
0
0
1
1
.
(,,,,)
, 1, , 1,
α
tt
t
j
fy yt
tnjm
−
⎛⎞
⎜⎟
⎜⎟
⎝⎠
∂
===
∂
α x
D
При использовании комбинированного критерия качества
22 2
0000 0 000
11 22
() ββ
y
WW W
Δ=−Δ +⋅Δ−Δ +⋅−Δ
y α
Φα eDααR α eDα
алгоритм адаптации по определению вектора параметров α по аналогии
с (3.1.6) , (3.2.7) сводится к итерационной процедуре вида:
00
11
11
111 222
1
11 21
, 1, 2, 3, ....
( ββ)
( ββ).
ii i
i
TTTii
y
y
TT Ti
yr
y
hi
−−
−−
−
⎧
⎪
⎪
⎨
⎪
⎪
⎩
=+Δ =
++ Δ=
=+Δ+
α
α
αα α
DWD RWR DWD α
DWe RW α DWe
(3.4.3)
По аналогии с (3.4.3) проектируются алгоритмы адаптации для ин-
тегрированных систем идентификации, где в качестве модели объекта
используются нелинейные интегральные уравнения вида (1.2.11).
49
Глава 4
НЕПАРАМЕТРИЧЕСКИЕ ИНТЕГРИРОВАННЫЕ
СИСТЕМЫ ИДЕНТИФИКАЦИИ
4.1. Линейные непараметрические интегрированные системы идентификации
Рассмотрение непараметрических интегрированных систем иден-
тификации начнем с простой интегрированной системы моделей перво-
го уровня вида
*
,
αφ(α ) η , 1, ,
jjj j
j
m
⎧
⎪
⎨
⎪
⎩
=+
=+=
yFαξ
(4.1.1)
где
F – вектор известных функций ,,1 ),( mjf
j
=x вычисленных в точках
,1,;
i
in=x
*** *
12
(, , , )
T
n
yy y=y …
– вектор измеренных значений выхода
объекта у; α – вектор неизвестных параметров;
α , 1,
j
j
m
=
– дополни-
тельные априорные данные;
φ (α ), 1,
jj
j
m
=
– неизвестные однозначные
функции, связывающие параметры исследуемого объекта с выходными
значениями объекта-аналога;
, η , 1, ,
j
j
m
=
ξ – случайные величины,
представляющие ошибки измерения выхода объекта и ошибки задания
априорной информации; Т – символ транспонирования.
Задача идентификации заключается в оценивании неизвестных па-
раметров, когда относительно функций
φ (), 1,
j
j
m
=
α известны лишь
общие предположения, такие как непрерывность, ограниченность, су-
ществование производных и т. д.
В данных условиях модель (4.1.1) представляет линейную, интег-
рированную систему, где дополнительная информация задана в непара-
метрической форме. Существует достаточно широкий класс объектов с
непараметрическими моделями априорной информации:
1.
Системы, где априорные данные неоднородны.
2.
Системы, где недостаточно изучен механизм взаимодействия
исследуемого объекта и объекта-аналога.
3.
Системы с нестабильным взаимодействием исследуемого объек-
та и объекта-аналога (при одних условиях есть взаимодействие, при
других условиях – нет) и т. п.
В условиях непараметрической априорной неопределенности о
структуре моделей объектов-аналогов, когда функции
φ (), 1,
j
j
l=α не-
известны, встает вопрос о методике формирования комбинированного
функционала качества. Сформулируем критерии, необходимые для кон-
струирования комбинированного функционала качества [12].
50
1. Критерий огрубления моделей объектов-аналогов
Действие критерия заключается в замене неизвестной функции
φ ()
j
α известной в окрестности некоторой точки α
0
. В простейшем случае
в качестве φ ()
j
α может быть выбран вектор неизвестных параметров α.
2. Критерий значимости дополнительной информации
Данный критерий предусматривает введение правила «менее зна-
чимой дополнительной информации – меньший вес», что связано с вве-
дением некоторых весовых функций с центром в окрестности точки
0
α
j
,
убывающих в зависимости от увеличения значений
0
αα
jj
−
→∞.
3. Критерий компенсации
В качестве компенсации за огрубление моделей дополнительных
априорных данных, выбора начального приближения
0
α
j
параметра
α
j
,
вводится весовая функция с управляющим параметром
h
0
αα
j
j
K
h
⎛⎞
⎜⎟
⎜⎟
⎝⎠
−
,
таким образом, чтобы выполнялись условия 0, 0, , .
hh
K
hKCh→→ →<∞→∞
В качестве комбинированного функционала качества с учетом вве-
денных выше критериев, будем использовать приближение
2
2
*
() () () ,
h
y
=+ =− +−
K
W
Φα J α Q α yFααα
(4.1.2)
где ()
J α – взвешенный с матрицей
y
W
частный критерий среднего квад-
рата ошибок измерений выхода объекта и выбора модели; ( )
Q α – частный
критерий качества модели объекта-аналога;
0
αα
((( ),
j
j
h
diag K
h
−
=
K
1, )
j
m= – диагональная матрица весовых функций, h – управляющий
параметр.
Следует отметить, что аналогом данных весовых функций являют-
ся ядра в непараметрических оценках плотности распределения вероят-
ностей и регрессии, приведенных в приложении 3.
Задача определения параметров
α с учетом критерия (4.1.2) сводит-
ся к задаче оптимизации вида
*
() argmin ().h
=
α
αΦα (4.1.3)
Для решения задачи (4.1.3) необходимо взять производные от
функционала ()
Φα по параметрам α, используя формулы для производ-
ных по векторному аргументу, приведенные в приложении, и прирав-
нять их к нулю:
*
2( )2()0.
T
y
h
∂
=∇ =− − − − =
∂
α
Φ
Φ FW y Fα K αα
α
