Сергеев В.Л. Интегрированные системы идентификации
Подождите немного. Документ загружается.

81
Математическая модель извлекаемых запасов ()
s
α представляет
некоторую площадь, заключенную между функцией (, )
f
t α и осью вре-
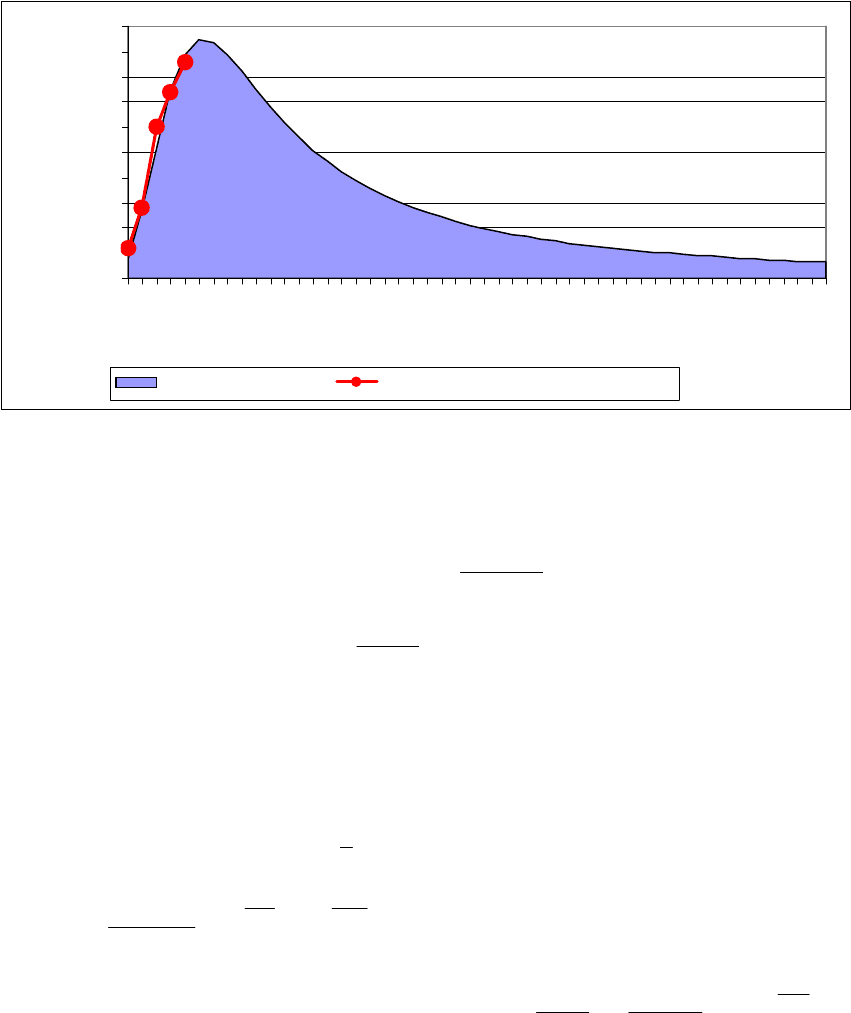
мени от начала до окончания разработки месторождения. На рис. 6.1, в
качестве примера, изображены фактические и модельные значения до-
бычи нефти. Извлекаемые запасы – залитая область. В качестве модели
добычи использовалась функция
3
α
12
.(, ) α exp( α )
f
ttt
=
−α
0
50000
100000
150000
200000
250000
300000
350000
400000
450000
500000
1 3 5 7 9 1113151719212325272931333537394143454749
Число лет разработки
Добыча нефти в тоннах
Извлекаемые запасы Факт ические значения добычи нефт и
Рис. 6.1. Извлекаемые запасы
Представление моделей добычи нефти и извлекаемых запасов ря-
дом Тейлора в некоторой точке начальных значений параметров
α
0
000
1
00000
1
,
,
(, )
(, ) (, ) ( ) α
α
()
() ( ) ( ) αα(αα)
α
m
j
i
i
m
j
jii
i
i
f
t
ft ft
s
ss
=
=
∂
≅+ ⋅Δ
∂
∂
≅+ ⋅ΔΔ=−
∂
∑
∑
α
αα
α
αα
(6.1.4)
позволяет перейти от нелинейной интегрированной системы моделей
(6.1.2) к линейной относительно приращений вектора параметров
)α,...,α,α(
00
2
0
1
0
l
ΔΔΔ=Δα
:
000
000
,
,
ff
ss
⎧
⎪
⎨
⎪
⎩
=
Δ+
=
Δ+
eDαξ
eDαη
(6.1.5)
где
0
0
,1 , ,1 ,
α
),(
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
==
∂
∂
= mjni
tf
j
i
f
α
D
– матрица частных производных от функ-
ции f(t,
α) по параметрам α = (α
1
, α
2
, …, α
m
);
0
0
0
,1 ,τd
α
),τ(
α
)(
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∂
∂
=
∂
∂
=
∫
mj
fs
T
jj
s
αα
D
–
82
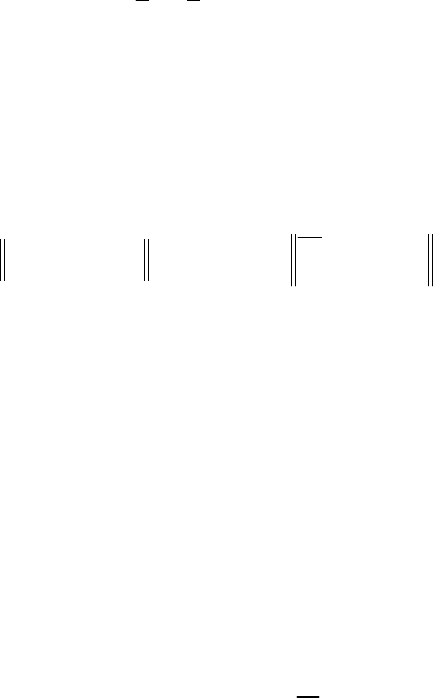
вектор частных производных от функционала ()
s
α ;
0* 0
(, )
f
t=−eqfα –
вектор начальных значений невязок между фактическими и модельны-
ми значениями добычи нефти;
00
()
s
s
=
−es α – вектор начальных значе-
ний невязок между дополнительными априорными значениями извле-
каемых запасов нефти и значениями запасов нефти, вычисленными по
модели. Индекс «0» означает, что все частные производные вычислены
при значениях
0
.
=
αα
Для линейной интегрированной системы моделей (6.1.5) комбини-
рованный критерий качества
Φ
примет вид:
.β)(
1
2
)(
000
2
)(
0000
∑
=
Δ−⋅+Δ−=Δ
l
k
sW
ssk
yW
ff
αDeαDeαΦ
(6.1.6)
Комбинированный критерий качества (6.1.6) с использованием ме-
тода Гаусса–Ньютона позволяет получить оптимальные значения при-
ращений параметров на первом и последующих шагах итерационного
процесса:
1
11*
1* 1
(),
1, 2, 3, .. . .
()argmin(),
i
ii i
i
ii
h
i
−
−−
−−
⎧
⎪
⎨
⎪
⎩
=+Δ
=
Δ= Δ
Δα
αα α
αΦα
(6.1.7)
Оптимальные значения параметров
*1
)(
−
Δ
i
α
на каждом шаге
1, 1, 2, 3, .. .
ii−= определяем из решения системы линейных уравнений
11*
k
1
001
k
k1
( β )( )
( β ).
l
TTii
ysss
ff
k
l
TTi
yrss
ff
−−
=
−
=
+⋅ Δ=
=+⋅
∑
∑
DWD DWD α
DWe DWe
(6.1.8)
Для получения (6.1.8) достаточно вычислить производные от
0
()ΔΦα по
0
Δα и приравнять их к нулю.
В качестве критерия окончания итерационного процесса (6.1.7) (ос-
танова) используем величину
1
(() ( ))/ ()δ, 1, 2, 3, ...
ii i
i
−
−≤=Φα Φα Φα
, (6.1.9)
где δ – заданное значение точности. Тогда оптимальным вектором па-
раметров
*
()αβ
считаем такое значение ,1,2,3,...
i
i
=
α , при котором вы-
полняется неравенство (6.1.9).
Следует отметить, что на каждом шаге итерационного процесса
(6.1.7) должен быть определен оптимальный вектор управляющих па-
раметров
*
β (6.1.3) и осуществлена проверка условия сходимости
1
(() ( )
ii
−
≤
Φα Φα , (6.1.10)
которое говорит, что величина правой часть неравенства (6.1.9) должна
быть положительной.

83
Следует отметить, что при известных статистических характери-
стиках ошибок измерений добычи нефти ξ для определения управляю-
щих параметров может быть использован метод невязки, рассмотрен-
ный в пятой главе.
Рассмотрим алгоритм адаптации интегрированной модели (6.1.2) с
использованием итерационной процедуры (6.1.7), предполагая,
что
*
() ()
I
==Wy Ws , где
I
– единичная матрица.
3. Алгоритм адаптации:
1.
Для выбранной модели добычи нефти (6.1.1) задается номер
шага 0
i = , начальные приближения вектора параметров α
0
и начальные
значения вектора управляющих параметров β
0
.
2.
Формируется система линейных уравнений (6.1.8). Вычисляются
приращения вектора параметров путем решения системы линейных
уравнений одним из методов, приведенных в приложении 4.
3.
Проверяется условие сходимости (6.1.10). При невыполнении
этого условия осуществляется выбор величины шага
*
() argmin ( )
i
i
iii
h
hh=+⋅ΔΦα α
(6.1.11)
одним из методов оптимизации, рассмотренным в приложении 3 . В ме-
тоде Гаусса–Ньютона (6.1.7) производится дробление шага
i
h пополам
/2
ii
hh= .
4.
При выполнении условия сходимости производится вычисление
первого приближения параметров
1*
() ( ())
ii i ii
i
h
+
=
+Δαβ α αβ
(6.1.12)
и вычисляются оптимальные значения управляющих параметров
2
**1
() argmin( (( ())
i
iii+
==−
β
β Jqfαβ
(6.1.13)
с использованием методов оптимизации функций, приведенных в при-
ложении 3.
5.
Проверяется условие останова (6.1.9), при выполнении которого
процедура адаптации заканчивается, и оптимальные значения парамет-
ров модели и управляющих параметров выбираются равными
*1* *
,()
ii
+
=
=αα β β
.
При невыполнении условия останова осуществляется поиск сле-
дующего приближения параметров. Производится увеличение номера
шага на единицу 1ii=+, начальным значениям параметров модели и
управляющим параметрам присваиваются значения, полученные на
первом шаге итерационного процесса
1*
,()
ii i
+
=
=αα ββ
,
и осуществляется переход к пункту 2.

84
По завершению алгоритма адаптации прогноз добычи нефти
ˆ
( τ)qt+
с момента времени t на период τ и уточненная на момент време-
ни
t оценка извлекаемых запасов определяются по формулам:
**
**
0
ˆ
( τ)(τ,()),
.
ˆ
() (τ,())dτ
T
qt f t
st f
+
=+
=
∫
αβ
αβ
(6.1.14)
Качество прогноза добычи нефти проверяется с использованием
критерия
*
*
ˆ
( τ)(τ)
δ(τ) ε,
( τ)
qt qt
qt
+− +
=≤
+
(6.1.15)
где ε – заданная точность,
τ ,1,ti i n
=
Δ⋅ = .
Если качество прогноза добычи нефти неудовлетворительное (кри-
терий (6.1.15) не выполняется), производится переход к другой интег-
рированной системе моделей и осуществляется процесс ее адаптации.
6.2. Идентификация гидродинамических исследований скважин
1. Введение. Гидродинамические методы исследования скважин
(ГДИС) занимают важное место в комплексе проблем информационно-
го обеспечения разработки нефтяных и газонефтяных месторождений.
Основным, наиболее информативным видом ГДИС, является исследо-
вание скважин на неустановившихся режимах, получение и анализ кри-
вых восстановления давления (КВД), которые представляют процесс
изменения во времени забойного давления после остановки
скважины.
В качестве модели КВД в зависимости от типа нефтяного пласта широ-
ко используются нелинейные функции вида:
()
()
()
0
зз
0
2
0
зз
0
2
зз
00
2
q μ
2, 25χ
() ( ) log( ),
4π
μ
2, 25
() ln χ 2,
4π
μ 2, 25χ
() ( ) ( ()) ln /2 () ,
4π
c
k
c
c
t
Pt Pt
kh
r
q
Pt Pt t s
kh
r
t
Pt Pt q qt qt qt
kh
r
⎛⎞
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
⎡
⎤
⎢
⎥
⎢
⎥
⎣
⎦
=+
=+ +
=+− − +
(6.2.1)
где
з
()Pt – забойное давление в момент времени t;
(
)
з
0
Pt – забойное дав-
ление в начальный момент времени t
0
; q
0
– дебит скважины до ее оста-
новки; k – проницаемость пласта; h – толщина пласта; μ – вязкость неф-
ти; χ – пьезопроводность пласта;
2
c
r – радиус скважины;
k
s
– скин-
фактор скважины; ( )qt – дебит скважины после ее остановки.

85
Задача идентификации заключается в определении вида модели
КВД и фильтрационных параметров нефтяного пласта и скважины
k , χ ,
k
s
на основе измерений забойного давления.
Рассмотрим решение данной задачи на основе интегрированных
систем моделей с учетом дополнительной априорной информации о
пластовых давлениях, фильтрационных параметрах пласта, накоплен-
ной добыче нефти после остановки скважины.
2. Идентификация КВД с учетом априорной информации о
пластовых давлениях.
При использовании дополнительной информа-
ции о пластовом давлении имеет место интегрированная система моде-
лей вида [27]:
0
*
ззз
0
пл
kk
() ( ) (, ξ ,1,,
(τ,)
d τη (,) η ,1,,
τ
iii
T
k
з
t
Pt Pt Pt i n
dP
PPTkl
d
⎧
⎪
⎪
⎨
⎪
⎪
⎩
=+ +=
=+=+=
∫
α)
α
α
(6.2.2)
где
*
з
(), 1,
i
Pt i n= – измеренные значения забойного давления в моменты
времени t
i
;
з
(, )Ptα – модель КВД (функция вида (6.2.1));
12
(α , α , ...., )
m
α
=
α –
вектор неизвестных параметров модели, связанный с соответствующи-
ми значениями фильтрационных параметров пласта;
,1,
k
пл
Pk l=
– экс-
пертные оценки пластового давления;
з
0
()Pt – начальное значение за-
бойного давления в момент остановки скважины
t
0
;
ξ ,1,,η
i
in=
– неко-
торые случайные величины, представляющие ошибки измерения КВД и
ошибки задания априорной информации о пластовом давлении.
Математическая модель пластового давления
пл
P представляет неко-
торую площадь, заключенную между производной от забойного давле-
ния и осью времени до максимального значения времени снятия КВД
T.
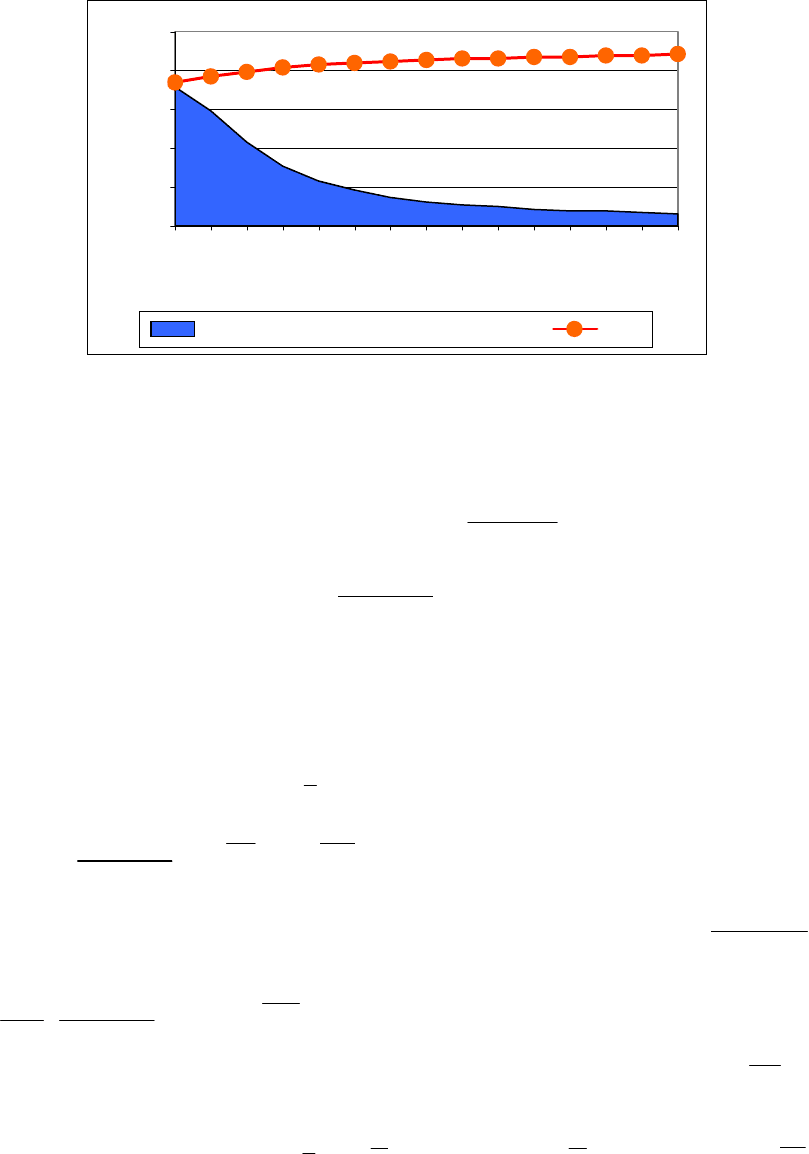
На рис. 6.2 в качестве примера изображены измеренные значения
забойного давления с интервалом измерения 1 час и значения производ-
ной от давления.
В качестве модели КВД использовалась функция, учитывающая
влияние ствола скважины (приток жидкости к скважине с дебитом
2
(,α )qt после ее остановки)
зз
010 2 3 4 2 0 2
(, ) ( ) α ((,α )(ln(α )2α ), ( ,α )exp(α ),Pt Pt q qt t qt q t=+− + = −α (6.2.3)
где параметры
134
α , α , α
связаны с фильтрационными параметрами пла-
ста и скважины соотношениями:
13 4
2
μ 2, 25χ
α ,α ,α
4π
к
c
s
kh
r
=
==
.
86
0
50
100
150
200
250
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Длительность исследований(в часах)
Давление (в атм.)
Модель пластового давления
КВД
Рис. 6.2
Представление моделей КВД добычи и пластового давления рядом
Тейлора в некоторой точке начальных значений параметров
0
α :
00
з
ззз
0
1
00 0 0
1
(,
(, ( ) (, ( ) α ,
α
(,)
(,) (,) ( ) α , α (αα)
α
m
j
i
i
m
j
jii
i
i
Pt
Pt Pt Pt
PT
PT PT
=
=
∂
≅+ + ⋅Δ
∂
∂
≅+ ⋅ΔΔ=−
∂
∑
∑
α)
α) α)
α
αα
(6.2.4)
позволяет перейти от нелинейной интегрированной системы моделей
(6.1.1) к линейной относительно приращений вектора параметров
000 0
12
( α , α ,..., α )
l
Δ=Δ Δ Δα
:
000
зз
000
пл пл
,
,
⎧
⎪
⎨
⎪
⎩
=
Δ+
=
Δ+
eDαξ
eDαη
(6.2.5)
где
0
0
з
(, )
, 1, , 1,
α
p
i
j
Pt
injm
⎛⎞
⎜⎟
⎜⎟
⎝⎠
∂
===
∂
α
D
– матрица частных производных от
функции
з
(,Ptα) по параметрам
12
(α , α , ..., α )
m
=
α ;
0
пл
(,)
α
j
PT
⎛
⎜
⎝
∂
=
∂
=
α
D
0
з
0
(τ,)
d τ, 1,
ατ
T
j
dP
j
m
d
⎞
⎛⎞
⎟
⎜⎟
⎟
⎝⎠
⎠
∂
==
∂
∫
α
– вектор частных производных от функцио-
нала (,)PT α ;
0* 0 * 0
ззз зз
00
() (, ) ( () () (, ), 1,)
T
ii
Pt Р qt Pt Р tin
=
−− = −− =eq αα –
вектор начальных значений невязок между фактическими и модельными
значениями добычи нефти;
00 0
пл пл
пл
((,))((,),1,
k
PT P PT k l
=
−=− =eP αα –
вектор начальных значений невязок между экспертными оценками пла-
стового давления и значением пластового давления, вычисленным по
модели. Индекс «0» означает, что все частные производные вычислены
при значениях
0
.
=
αα

87
Для линейной интегрированной системы моделей (6.2.5) будем ис-
пользовать комбинированный критерий качества:
зпл
22
0000 000
з з пл пл
1
() β ,
l
k
WW
k
=
Δ=−Δ + ⋅ −Δ
∑
Φα eDα eDα
(6.2.6)
который позволяет получить оптимальные значения фильтрационных
параметров на всех шагах итерационного процесса:
1
11*
1* 1
(),
1, 2, 3, ... .
()argmin(),
i
ii i
i
ii
h
i
−
−−
−−
⎧
⎪
⎨
⎪
⎩
=+Δ
=
Δ= Δ
Δα
αα α
αΦα
(6.2.7)
Оптимальные значения параметров
1*
()
i
−
Δ
α
на шаге 1,i
−
1, 2, 3, ...i = определяем из решения системы линейных уравнений:
11*
ззз плплпл
k
1
001
ззз плплпл
k
k1
( β )( )
( β ).
l
TTii
k
l
TTi
−−
=
−
=
+⋅ Δ=
=+⋅
∑
∑
DWD D W D α
DWe D We
(6.2.8)
Для получения (6.1.8) достаточно взять производные от
0
()ΔΦα по
0
Δ
α
и приравнять их к нулю.
В качестве алгоритма адаптации интегрированной модели по опреде-
лению фильтрационных (6.2.7) и оптимальных управляющих параметров
2
***
arg min( ( ( ))=−
β
β qPαβ
может быть использована процедура, аналогичная рассмотренной в
третьем пункте предыдущего параграфа.
3. Идентификация КВД с учетом априорной информации о
фильтрационных параметрах нефтяного пласта. При использовании
дополнительной априорной информации о фильтрационных параметрах
нефтяного пласта и скважины, полученной на объектах-аналогах, по
аналогии с (6.2.1), используем интегрированную систему моделей вида:
*
ззз
0
k
() ( ) (, ξ ,1,,
η ,1,,
iii
kk
Pt Pt Pt i n
kl
⎧
⎪
⎨
⎪
⎩
=+ +=
=+ =
α)
αα
(6.2.9)
где
(, 1,)
kk
kn==αα
– дополнительные априорные данные о фильтраци-
онных параметрах нефтяного пласта и скважины
),...,,(
21 m
αα
α
=
α
, по-
лученные с
l объектов – аналогов.
Для интегрированной системы моделей (6.2.9) алгоритм определе-
ния фильтрационных параметров при использовании метода Гаусса–
Ньютона и комбинированного функционала качества
з
2
2
0
0000 0
зз
1
() βα
l
k
k
W
W
k
=
Δ=−Δ + ⋅Δ−Δ
∑
α
Φα eDαα,
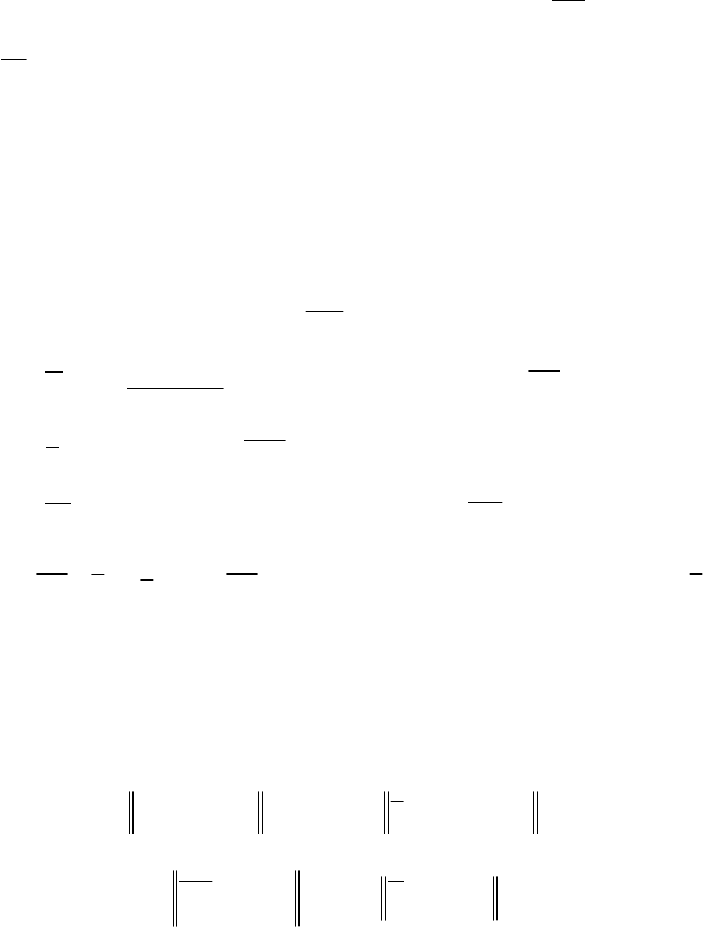
88
по аналогии с (6.2.7), сводится к последовательному решению системы
линейных уравнений:
1
11*
1* 1
0
11* 0 1
ззз ззз пл
kk
1k1
,
(),
( ) arg min ( ), 1, 2, 3, ...,
( β )( ) ( β )
i
ii i
i
ii
ll
TiiT i
k
k
h
i
I
−
−−
−−
−− −
==
⎧
⎪
⎨
⎪
⎩
=+Δ
Δ= Δ =
+Δ=+⋅Δ
∑∑
Δα
αα α
αΦα
DWD α DWe W α
(6.2.10)
где
β ,1,
k
kl=
– управляющие параметры,
I
– единичная матрица.
4. Комбинированные алгоритмы адаптации с учетом априор-
ной информации. При использовании дополнительной априорной ин-
формации о пластовых давлениях, фильтрационных параметрах нефтя-
ного пласта, априорной информации о накопленной добыче нефти по-
сле остановки скважины, полученных на
321
lll
+
+
объектах-аналогах,
необходимо использовать интегрированную систему моделей вида:
0
0
*
з
пл
1
k1 k
2
k2
23
k3 k3
() (, ξ ,1,,
(τ,)
d τη (,) η ,1,,
τ
η ,1,,
(τ,)dτη S( ) , 1, ,
iii
T
k
з
t
kk
T
k
t
Pt ft i n
dP
PPTkl
d
kl
Sq kl
η
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
=+=
=+=+=
=+ =
=+=+=
∫
∫
α)
α
α
αα
αα
(6.2.11)
где
*
зпл
(), 1,, , , 1,,
i
k
Pt i nP k nZ==α определены в (6.2.2), (6.2.9);
k
S –
экспертная оценка накопленной за время Т добычи нефти после оста-
новки скважины.
Для данной интегрированной системы моделей алгоритм определе-
ния вектора фильтрационных параметров при использовании метода
Гаусса–Ньютона и комбинированного функционала качества
1
3
2
зпл
22
0000 000
з з пл пл
1
1
2
2
0
0
1
11
() β
β () ,
s
l
k
WW
k
l
l
kk
k
W
kk
W
SS
=
==
Δ=−Δ + ⋅ −Δ +
+⋅Δ−Δ+ −
∑
∑∑
α
Φα eDα eDα
αα α
по аналогии с алгоритмами (6.2.7), (6.2.10), сводится к последователь-
ному решению систем линейных уравнений:
1
11*
1* 1 1 1 1
(),
( ) arg min ( ) ( ) , 1, 2, 3, ...,
i
ii i
i
iiii
h
i
−
−−
−−−−−
⎧
⎪
⎨
⎪
⎩
=+Δ
Δ= Δ= =
Δα
αα α
αΦαAB
(6.2.12)

89
где
3
1
ззз плплпл
k1 k2 2
111
( βββ() ()),
l
ll
iT T T
s
k
kkk
I
SS
−
===
=+ ++
∑∑∑
ADWD DWD DWD
3
12
0
10 0 1
ззз плплпл пл
k1 k2 2
k1 k1 1
( βββ() ()) ,
l
ll
iT T i
k
s
k
k
SS
− −
===
=+⋅ +⋅Δ+
∑∑∑
BDWe DWe Wα DWE
()
()
()
1
,1,
.
(), 1,
α
,
k
j
S
jm
SS k l
SS
∂
⎛⎞
=
−=
⎜⎟
∂
⎝⎠
==
α
DE
6.3. Планирование сокращенных испытаний на безотказность
технических систем
Создание сложных высоконадежных технических систем требует
разработки новых подходов к планированию испытаний на надежность,
поскольку рост требований к качеству продукции приводит к необхо-
димости проведения больших объемов испытаний для установления и
подтверждения заданных показателей надежности.
Так, для подтверждения средней наработки для отказа 3000 часов
продолжительность контрольных испытаний созданной системы при
самом благоприятном
исходе (отсутствии отказов) составляет при двух-
сменной работе более полутора лет. Минимальная продолжительность
определительных испытаний для установления средней наработки до
отказа составляет 5450 суток при доверительной вероятности
8,0=
γ
и
относительной ошибке оценки этого показателя равной 20 % (согласно
ГОСТ 27.52–83. Надежность в технике. Система сбора и обработки ин-
формации. Планирование наблюдений).
Рассмотрим суть задачи планирования определительных испытаний
на безотказность на примере классической модели отказов n, поставлен-
ных на испытания невосстанавливаемых однотипных технических систем
ξ ,1,
ii
tin
=
Δ+ = , (6.3.1)
где t
i
– наработка до отказа (время безотказной работы) технической сис-
темы с номером i, Δ – средняя наработка до отказа, ξ
i
– случайные вели-
чины, характеризующие действие на систему различных неучтенных
факторов, распределенные по нормальному закону с нулевым средним
значением и дисперсией
2
ξ
σ
. Известно (приложение 2. Статистические
оценки), что оптимальной оценкой средней наработки на отказ в данном
случае является выборочное среднее
*
1
1
,
n
i
i
t
n
=
Δ=
∑
(6.3.2)
распределенное по нормальному закону со средним значением
Δ , дис-
персией, равной
n/
2
ξ
σ
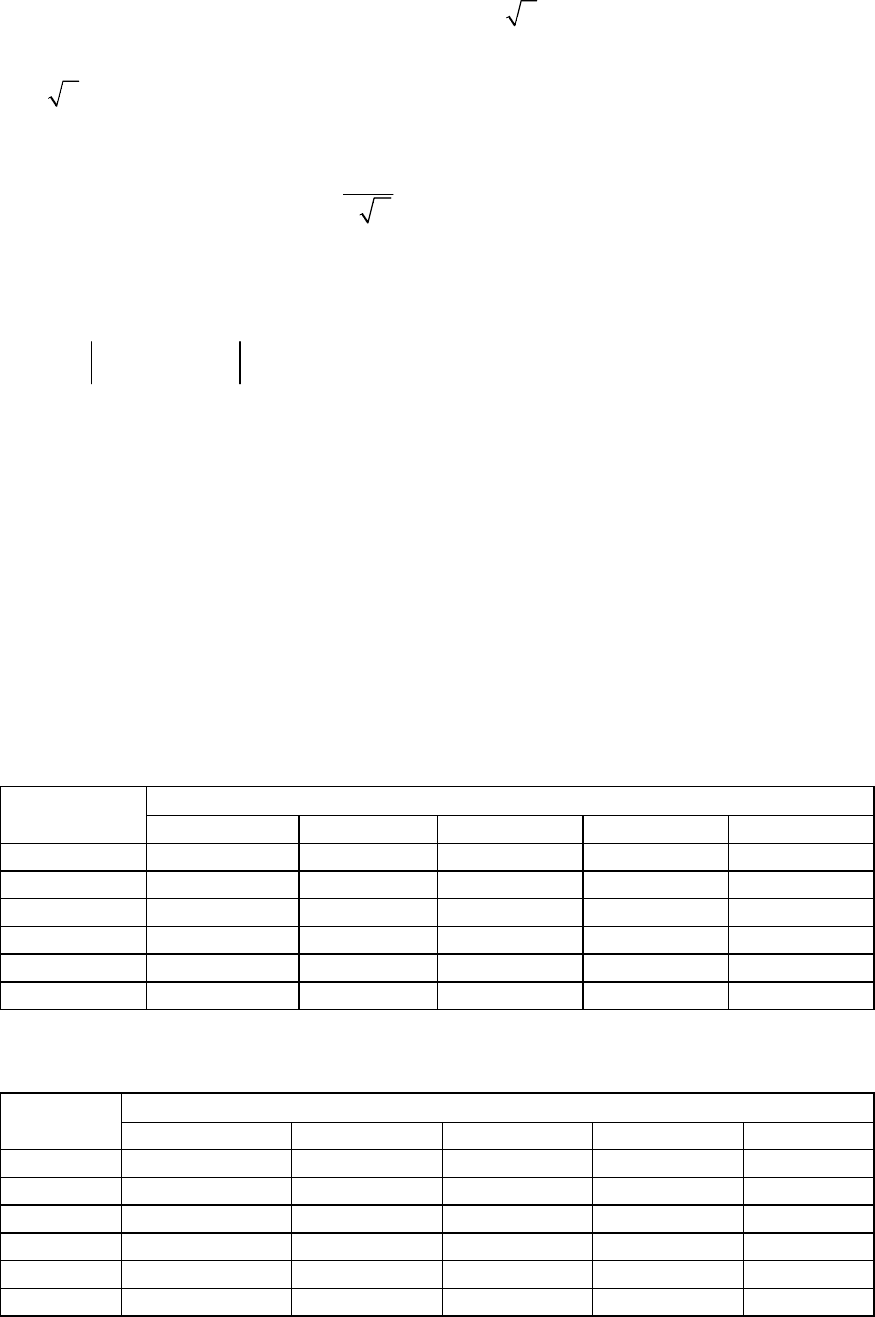
, и доверительным интервалом
90
*
н, вγ
ξ
σ /,tnΔ=Δ±
(6.3.3)
где
Δ
н
и Δ
в
– соответственно нижняя и верхняя доверительные границы;
ξ
σ / n – среднеквадратическое отклонение; t
γ
– квантиль уровня γ, оп-
ределяемый из условия
γ
2
γ
0
1
Ф() exp( )
γ
/2.
2 π
t
txdx=−=
∫
План испытаний, соответствующий количеству поставленных на
испытание систем либо числу отказов, находим из (6.3.3)
2
0
)/( δσ=
ξy
tn
, (6.3.4)
где
**
/)( ΔΔ−Δ=δ
в
– относительная ошибка оценки наработки до отказа.
Следует отметить, что минимальное число отказов при относи-
тельной ошибке
25,0=δ
и предельно допустимом по ГОСТ значении
доверительной вероятности γ = 0,8 равно 25 (n
0
= 25). Получение такого
количества отказов (или наличие поставленных на исполнение систем)
не всегда возможно на практике.
Для примера, в табл. 6.1 приведены планы определительных испы-
таний на безотказность, полученные на основе (6.3.4) при разных значе-
ниях точности и достоверности. В табл. 6.2. приведена продолжитель-
ность определительных испытаний в сутках, соответствующая приве-
денному в табл. 6.1
плану испытаний.
Таблица 6.1
Планы определительных испытаний на безотказность n
0
δ
γ
0,05 0,1 0,15 0,20 0,25
0,95 1600 400 177 100 64
0,9 1075 269 120 67 43
0,85 829 207 92 52 33
0,8 655 164 73 41 25
0,75 538 135 60 34 22
0,7 519 130 58 32 21
Таблица 6.2
Значения продолжительности испытаний на безотказность в сутках
δ
γ
0,05 0,1 0,15 0,20 0,25
0,95 212800 53200 23541 13300 8512
0,9 142975 35777 15960 8911 5719
0,85 110257 27531 12236 676 4389
0,8 87115 21812 9709 5450 3325
0,75 71554 17955 7980 4522 2926
0,7 69027 17290 7714 4256 2793
