Сергеев В.Л. Интегрированные системы идентификации

Подождите немного. Документ загружается.

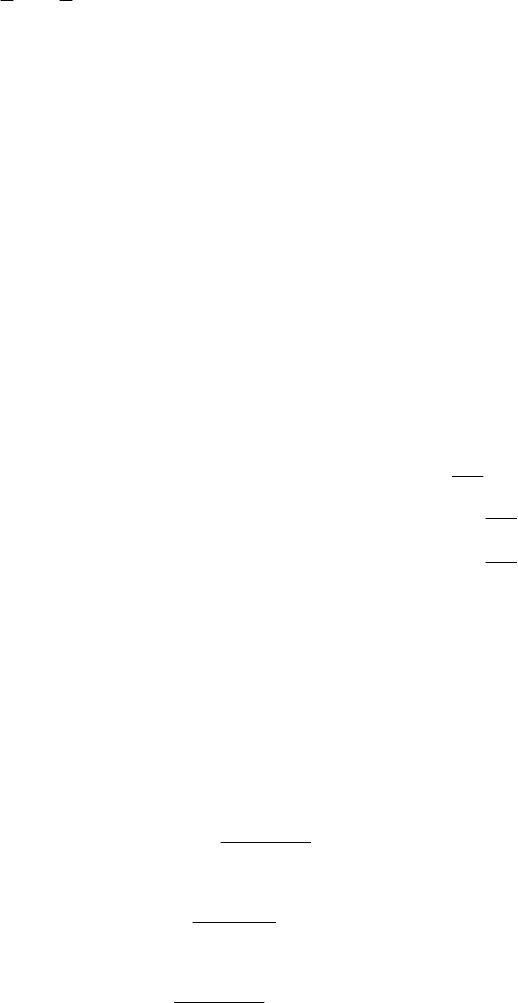
101

((,))

essT=−α – значение невязки между средним значением

имитируемых экспертных оценок извлекаемых запасов нефти и значе-

ниями запасов нефти, вычисленными по модели.

Индекс «1i − » означает, что все частные производные и функции в

скобках вычислены при значениях

, 1, 2, 3, ...

−

=αα .

Приведем описание алгоритма синтеза оптимальных оценок пара-

метров интегрированной системы моделей (7.2.11), реализованного во

втором разделе процедуры Sub Example_1_В1( ).

Алгоритм синтеза оптимальных оценок параметров

модели добычи нефти

1. Вычисление матрицы частных производных

D (все производ-

ные на первом шаге вычисляются при заданных начальных значениях

вектора параметров

),,(

ααα=α

exp( α ), 1,

Dttin=− =,

212 2

αα exp( α ), 1,,

Dttin=− − =

α 1

313 2

αα exp( α ),1,

tt i n

−

=− =.

2. Транспонирование матрицы

()

→ ()

D .

3. Вычисление произведения матриц

⋅

DD.

4. Формирование вектора строки

11 12 13

(, , )

DDD

D :

11 2

(τ, α)

( τ exp( ατ)ττ

∂

==−

∂

∫∫

12 1 2 2

(τ,α)

( τααexp( ατ)ττ,

Dd d

∂

==−−

∂

∫∫

α 1

13 1 3 2

(τ, α)

(dτααexp( ατ)τ d τ.

−

∂

==−−

∂

∫∫

5. Транспонирование вектора

D :

→DD

6. Расчет матрицы

⋅DD

7. Формирование матрицы планирования

β .

+ADD DD

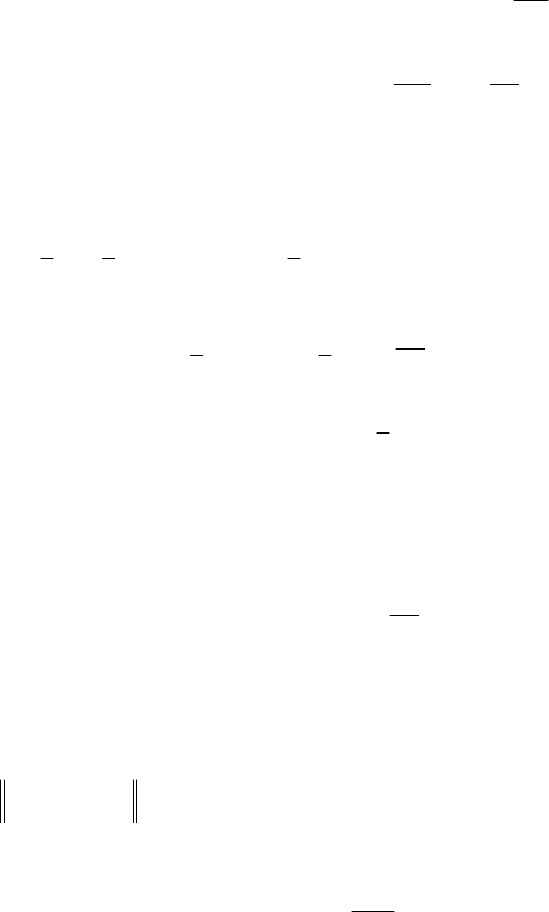
102

8. Вычисление вектора-столбца невязок между фактическими и мо-

дельными значениями добычи нефти

0* 0 * 0

.(, ) ( ( ) ( , ), 1, )

tqtftin

−=− =eqfαα

9. Формирование вектора-столбца

0*0

(( (,),1,, 1,3).

ji i i

Dy ft i mj=− ==De

10. Вычисление невязки между имитируемой средней экспертной

оценкой извлекаемых запасов и значением извлекаемых запасов, вычис-

ленных по модели

00 00

((,))(α exp( ατ)τ d).

sm m

essT s

=− =− −

∫

11. Вычисление вектора столбца

((), 1,3).

TT T

ss s

eDsei

12. Вычисление вектора-столбца свободных членов

β .

+BDe D .

13. Решение СЛУ

=A α B (процедура решения СЛУ Sub

EXP_hol_1() приведена в приложении 6) и получение приращений Δα

вектора параметров

(α , α , ..., α ).

=α

14. Определение первого приближения вектора параметров

10 0

αα α 1, 3

jj j

+Δ =

(параметр h на первом шаге равен 1).

15. Проверка условия сходимости метода Гаусса–Ньютона

() ( ),

≤Φ

где

**2

() () ( () (,).

MM M

qt ft

Φ= − = −

∑

α qq αα

Если условие сходимости не выполняется, то производится дроб-

ление шага

/2, 1,

hh i i

и переход к пункту 14 до выполнения условия 15. Целесообразно поста-

вить ограничение на число дробления шага, например 10

i = . Если ус-

ловие сходимости (15) выполняется, то проверяется условие точности

оценки параметров модели

10 0

(( ) ( )) ( ) ε,Φ−Φ Φ ≤αα/α

где ε – заданное значение точности. Если заданное значение точности

достигается, то процесс уточнения параметров заканчивается. В про-

тивном случае выполняется пункт 1 при

αα

103

Отметим, что при использовании оптимальной оценки управляю-

щего параметра

β следует решать оптимизационную задачу (7.2.8) на

каждом шаге приведенного выше алгоритма адаптации. Возможным ва-

риантом является также решение оптимизационной задачи (7.2.7) на

первом шаге метода Гаусса–Ньютона и использование полученных зна-

чений управляющих параметров на последующих шагах.

Завершением технологии статистического моделирования и соот-

ветственно результатами лабораторной работы № 1 являются расчет и

построение

следующей серии таблиц и графиков:

1) таблица и график зависимости относительной ошибки извлекае-

мых запасов

δ () ( )/ ), (τ,(β)) d τ

sabsssss f==−

∫

α (7.2.6)

от числа лет разработки месторождения n, где

– оценка извлекаемых

запасов за

n лет разработки месторождения;

2) таблица и график зависимости относительной ошибки прогноза

добычи нефти на L лет

δ (( )) ( ( ) (( ), (β)) / (( ), (β))),

Mnn n n n n n

qt L absq t L f t L f t L+= +− + +

αα (7.2.7)

от числа лет разработки месторождения ()

n n

tntLT

≤ ;

(β)

– оценки

вектора параметров модели добычи нефти, полученные по данным

лет разработки месторождения;

3) таблица и график зависимости относительной ошибки парамет-

ров интегрированной системы моделей

δ (α (β)) ((α (β) α )/α )1,

jn jn jn j j

abs j m=−= (7.2.8)

и среднего квадрата ошибки

α (β) α

δ ()

nj j

−

∑

(7.2.9)

от числа лет разработки n, уровня ошибок измерений добычи нефти c

уровня ошибок экспертных оценок извлекаемых запасов c

;

4) таблица значений вектора параметров модели

−

111

123

(α , α , α )

jjj−−−

= и приращений вектора параметров

( α ,

j−−

Δ=Δα

α , α )

jj−−

ΔΔ в зависимости от номера шага 1, 2, 3, ...

для заданной

реализации имитируемых значений добычи нефти и извлекаемых запа-

сов. Информация, приведенная в такой таблице, необходима для кон-

троля сходимости процесса поиска значений оценок параметров модели.

Все таблицы должны содержать усредненные значения информа-

ции о точности оценок параметров, как для одной реализации случай-

ных величин, так и для серии

реализаций.

104

Следует отметить, что приведенные критерии точности могут зна-

чительно отличаться в зависимости от параметра

k – номера реализации

случайных величин

,1,, , 1,, 1,.

ik jk

in jmkd

===ξ В этой связи поль-

зуются усредненными значениями относительных ошибок по всем реа-

лизациям

1,kd= :

δδ.

∑

(7.2.10)

Также отметим, что в силу того, что модель объекта нам известна и

известны значения определяемых параметров, в качестве оптимального

значения управляющего параметра β (либо вектора управляющих пара-

метров

(

β , β , ..., β ))

=β может быть использована его оптимальная

оценка

0*2

β arg min( (α (β) α )).

nj j

==−

∑

Φ (7.2.11)

В практических ситуациях в силу неизвестности модели, величину

управляющего параметра

получить невозможно. Можно получить его

различные эмпирические оценки

β ,1,

путем использования изло-

женных в третьем параграфе пятой главы методов. В этой связи возни-

кают вопросы точности оценок извлекаемых запасов и прогноза добычи

при использовании эмпирических оценок управляющих параметров

β ,1,

, где могут быть использованы критерии (7.2.6)–(7.2.9).

Например, относительная ошибка оценки извлекаемых запасов при ис-

пользовании эмпирических оценок управляющих параметров

β ,1,

определяется величиной

e δ (β )/δ (β ), 1,

jnjjn

c==, (7.2.12)

где

δ (β )

nj jn

δ (β )

– относительные ошибки извлекаемых запасов нефти.

В качестве примера на рис.7.2–7.4 приведены графики зависимости

относительной ошибки извлекаемых запасов и прогноза добычи нефти в

зависимости от числа лет разработки, начиная с первого года разработ-

ки месторождения, полученные в результате работы процедуры Sub Ex-

ample_1_B1( ).

Следует отметить, что рассмотренные выше примеры не охваты-

вают ряд важных

вопросов надежности, устойчивости оценок, анализа

их поведения в экстремальных ситуациях. Данные вопросы предлагают-

ся в качестве дополнительного задания к лабораторным работам.

105

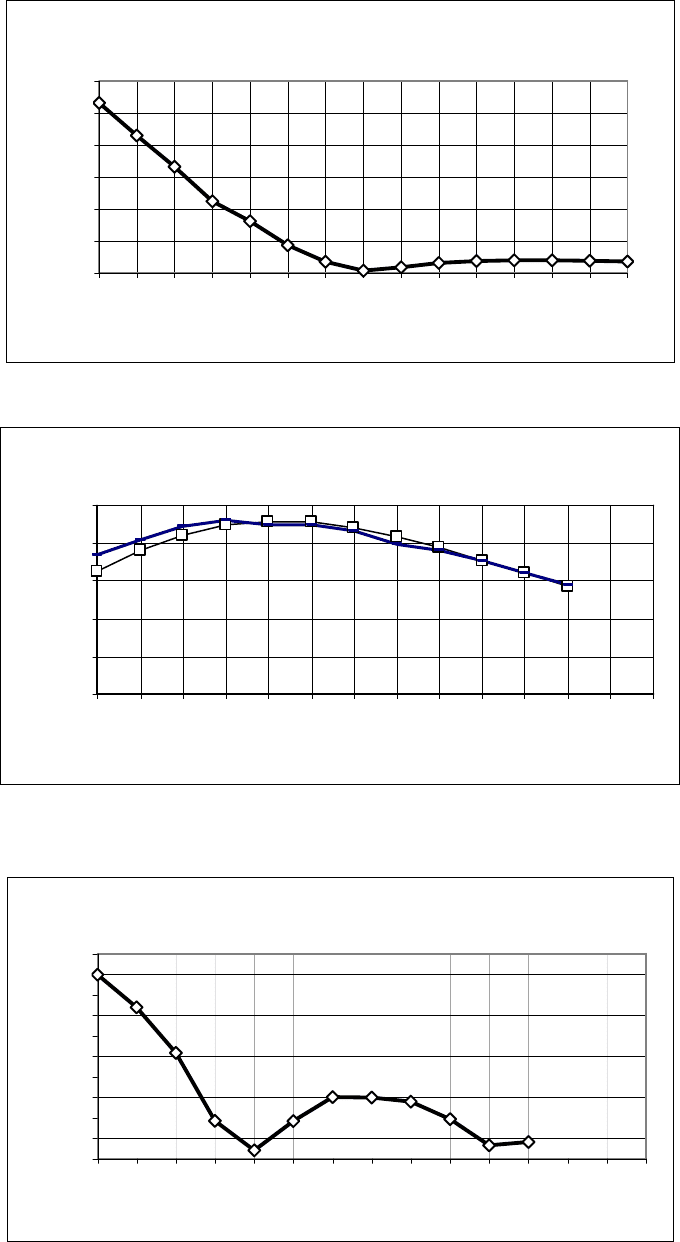
Точность оценки извлекаемыз запасов

0,00

0,05

0,10

0,15

0,20

0,25

0,30

123456789101112131415

Число лет истории разработки

Относительная ошибка

Рис .7.2. Относительная ошибка оценки извлекаемых запасов

Прогноз добычи нефти на 3 года

0,0

10,0

20,0

30,0

40,0

50,0

4 5 6 7 8 9 10 11 12 13 14 15

Число лет истории разработки

Добыча нефти в тыс. тонн

Рис .7.3. Прогноз добычи нефти: прогнозные значения – маркированная линия;

фактическая добыча нефти – сплошная линия

График точности прогноза добычи нефти

0,00

0,01

0,02

0,03

0,04

0,05

0,06

0,07

0,08

0,09

0,10

4 5 6 7 8 9 10 11 12 13 14 15

Число лет истории разработки

Относительная ошибка

Рис. 7.4. Относительная ошибка прогноза добычи нефти на три года

в зависимости от числа лет разработки месторождения

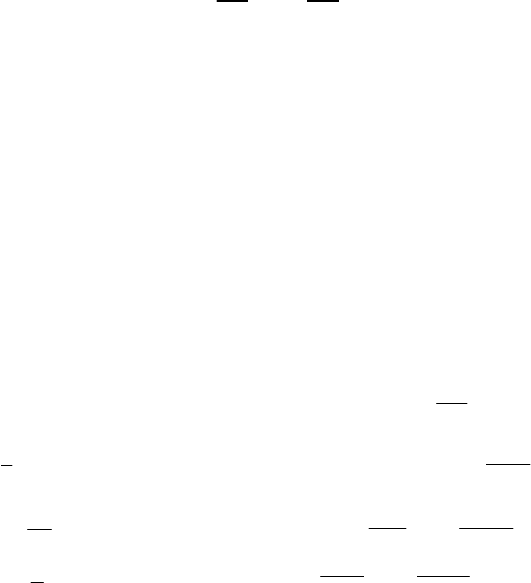
106

Например, в случае трех параметров за первые два года разработки

месторождения определить параметры модели добычи нефти традици-

онным методом наименьших квадратов невозможно в силу вырожден-

ности матрицы

DDв алгоритме определения параметров:

11*

11* 01

( ) , 1, 2, 3, ...,

()()().

ii i

Ti i Ti

ff ff

−−

−− −

⎧

⎪

⎨

⎪

⎩

=+Δ =

Δ=

αα α

DD α De

(7.2.13)

В этой связи важным показателем качества адаптированной интег-

рированной системы моделей является относительная эффективность

(устойчивость) оценок при переходе от стандартных (нормальных) ус-

ловий функционирования системы к экстремальным условиям (5.2.2), а

также относительная эффективность оценок в экстремальных условиях

их функционирования (5.2.3).

Экстремальные условия функционирования интегрированной сис-

темы моделей также имитируются

методами статистического модели-

рования.

Например, модель случайных величин с резко выделяющимися

значениями (выбросами) для моделирования исходных и дополнитель-

ных априорных данных может быть получена с помощью датчика псев-

дослучайных чисел:

ξξ,1,, 1,, , 1

ii j

xinjccn=+Δ = = ≤ Δ>>

где

– последовательности независимых псевдослучайных вели-

чин с нулевым средним значением и ограниченной дисперсией.

Следует отметить, что более полной для решения задачи прогноза

добычи нефти и оценки извлекаемых запасов является интегрированная

система моделей, в которой наряду с априорной информацией об извле-

каемых запасах дополнительно учитываются экспертные данные о до-

быче нефти (в

том числе ее прогнозные значения) и экспертные сведе-

ния о значениях оцениваемых параметров.

Такая модель, включенная в один из вариантов лабораторных ра-

бот, имеет следующий вид:

21 21 1

32 2

() (, (, ) , 1,,

(τ,)dτη (, ) η ,1,,

() (,) η ,1,, 1,,

αα η,1,,1,,

ii ii i

iji i i i

kkj kj kj k

qt ft c qt c i n

fcsTcjm

Gq t G f t cg i n j m

ГГc Г kmjm

⎧

⎪

⎨

⎪

⎩

=+=+=

=+==

=+ = =

∫

α) ξαξ

αα

(7.2.14)

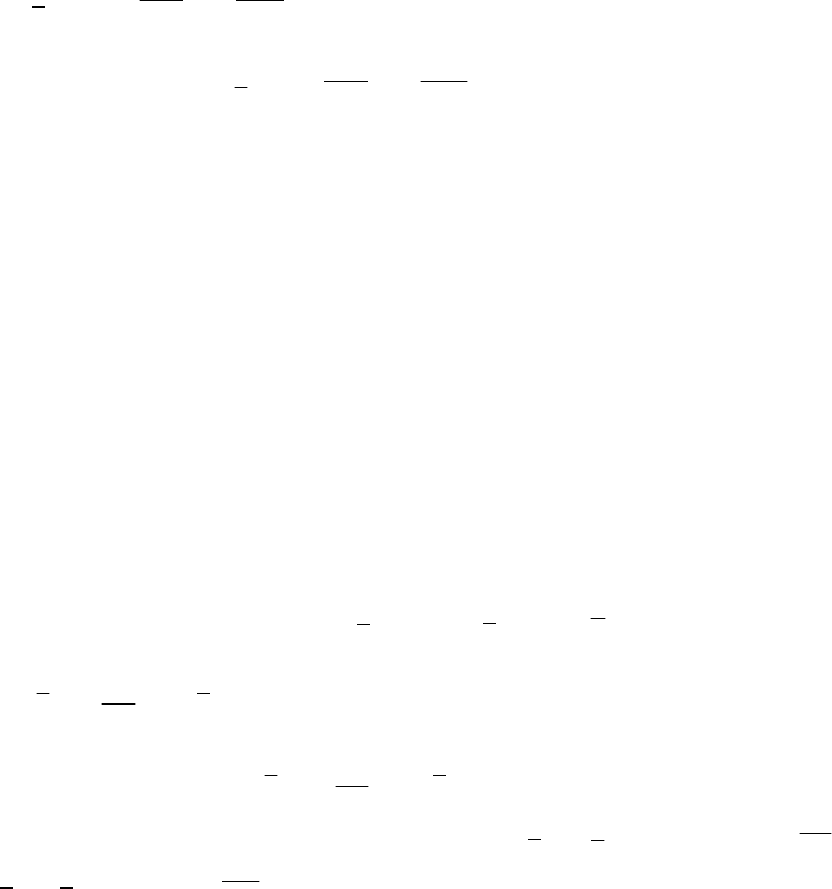
107

где

(), 1, , 1,

qt i m j m∈=

– дополнительные данные о добыче нефти, в

том числе и ее прогнозные значения, полученные из m

различных источ-

ников информации;

α ,1,,1,

kmjm== – дополнительные априорные

данные о параметрах модели добычи нефти, полученные из разных ис-

точников; G

и Г

– элементы диагональных индикаторных матриц G и Г,

принимающих значения ноль либо единица, где ноль означает отсутст-

вие априорной информации о соответствующих экспертных значениях

добычи нефти и экспертных значениях параметров модели. Остальные

переменные имеют смысл, приведенный в интегрированной системе

моделей (7.2.1).

Процедура определения оптимальных оценок вектора параметров

0000

123

(α , α , α )=α упрощенной модели (7.2.14) по аналогии с моделью

(7.2.4) с использованием квадратичного критерия качества и метода Гаусса–

Ньютона имеет вид:

11*

12 3

(),1,2,3,...,

( ββ β)( )

( ββ β),

ii i

TTT ii

ff f f

TTT i

ss g

ff f

−−

−

⎧

⎪

⎨

⎪

⎩

=+Δ =

++ +Δ=

=++ +Δ

αα α

DD DD DGD Гα

De D DGe Гα

где

()

im i j i

qGqt

∑

– среднее значение имитируемых экспертных

оценок добычи нефти,

αα

km k kj

∑

– среднее значение экспертных

оценок параметров модели добычи нефти,

((,),1,),

im i i

qGft in

−∈e α

((αα), 1, ),

km k

kmΔ= − ∈α

123

β , β , β – управляющие параметры.

Алгоритм синтеза оптимальных оценок параметров приведенной

процедуры аналогичен алгоритму, реализованному в процедуре Sub

Example_1_В1( ).

Приведем пример одного из вариантов лабораторной работы № 2,

целью которой является проведение исследований методом статистиче-

ского моделирования потенциальной точности и качества оценок

фильтрационных параметров нефтяного пласта на основе использова-

ния интегрированной системы

моделей кривой восстановления забой-

ного давления с учетом экспертных оценок пластового давления,

фильтрационных параметров пласта, экспертных оценок накопленной

жидкости в стволе скважины после ее остановки (6.2.11):

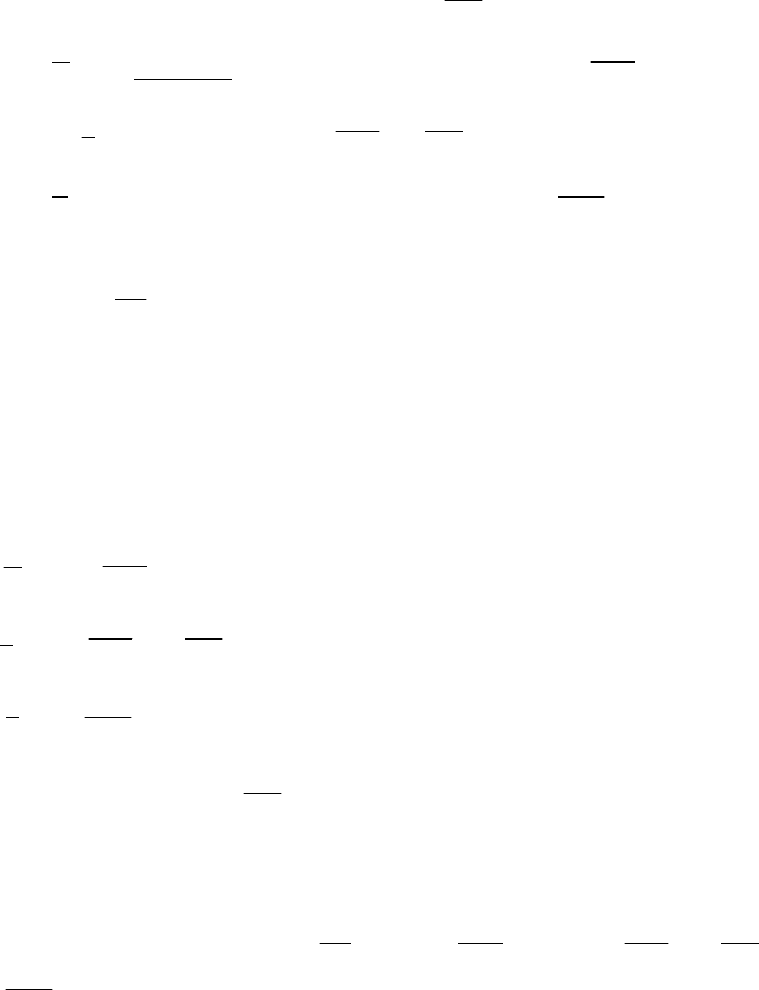
108

зз

пл

21 21 1

433

() (, , (), ξ ,1,,

(τ,)

d τη (,) η ,1,,

ααη,1,,1,,

(τ,)dτηS( , ) η ,1,,

ii i i

k kj k kj kj

Pt Pt t qt c i n

PcPTcjm

ГГckmjm

Sq c T jm

⎧

⎪

⎨

⎪

⎩

=+=

=+=+=

=+ = =

=+=+=

∫

α)

Gα Gα

(7.2.15)

где

(), 1,

Pt i n= – имитируемые значения забойного давления в мо-

менты времени

t ;

(, , (), )Ptt qt α

– модель кривой восстановления забойного дав-

ления;

– время остановки скважины;

(α , α , ..., α )

=α – вектор фильтрационных параметров нефтя-

ного пласта, включая параметры, входящие в модель дебита притока

жидкости в скважину после ее остановки;

пл

,1,

Pjm= – имитируемые значения экспертных оценок пла-

стового давления;

α ,1,,1,

kmjm∈= – имитируемые значения экспертных оценок

фильтрационных параметров нефтяного пласта;

,1,

Sj m= – имитируемые значения экспертных оценок накоп-

ленной жидкости в стволе скважины после ее остановки;

7) G и Г

(Г ,1,)

diag k m== – диагональные индикаторные матрицы;

8) ( , )qt Gα – модель притока жидкости после остановки скважины;

9) S( , )T Gα – модель накопленной за время

жидкости после ос-

тановки скважины;

10) случайные величины

,1,,

η ,1,,

η ,1,,1,,

kmjm==

η ,1,

m= по аналогии с (7.2.1) имеют смысл ошибок измерений за-

бойного давления и ошибок задания дополнительных априорных сведе-

ний (экспертных оценок).

Процедура определения оптимальных фильтрационных параметров

данной интегрированной системы моделей с использованием квадра-

тичных критериев качества и метода Гаусса–Ньютона подобна проце-

дуре, приведенной в (6.2.12) .

Однако практическая реализация данной процедуры вызывает

большие трудности, связанные с определением вектора управляющих

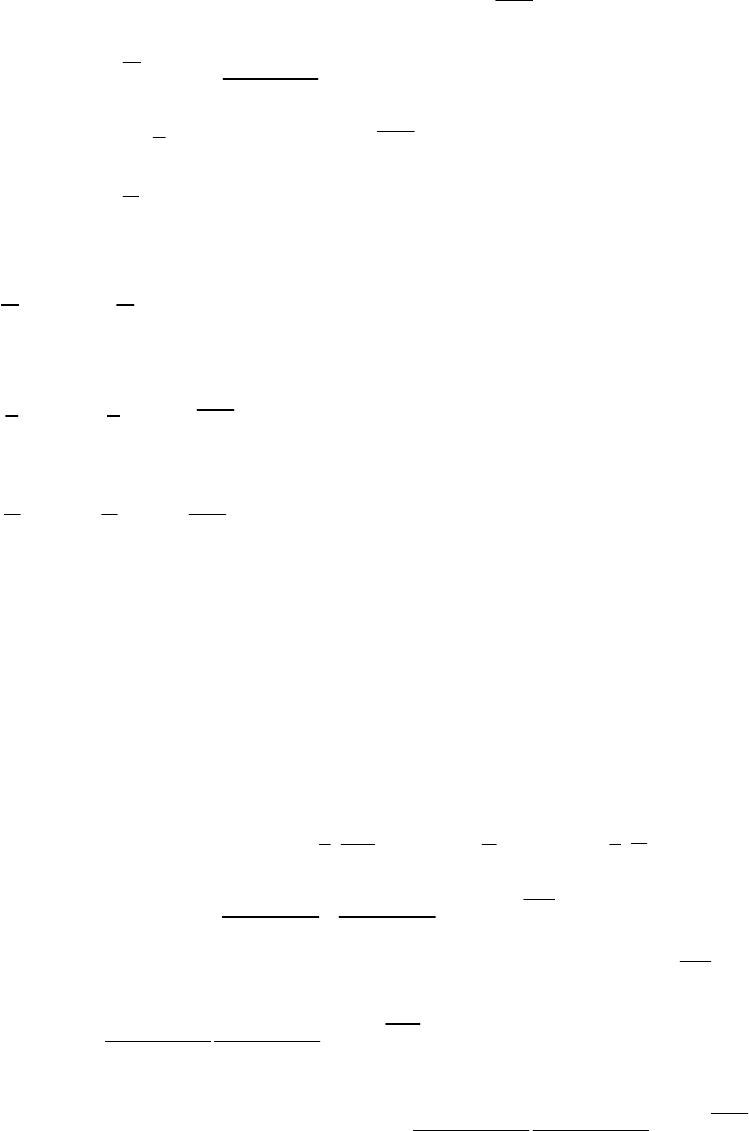
109

параметров размерности

123

lmm m=++, и уже при 10l > представляет

достаточно сложную оптимизационную задачу. Для упрощения проце-

дуры адаптации оценок перейдем к интегрированной системы моделей

кривой восстановления забойного давления вида:

зз

пл

() (, , (), ξ ,1,,

(τ,)

d τη (, ) η ,

ααη,1,,

(τ,)dτ (, ) η ,

iii i

kk kk

Pt Ptt qt c i n

PPT

ГГ km

Sq ST

⎧

⎪

⎨

⎪

⎩

=+=

=+=+

=+=

==+

∫

α)

Gα Gα

(7.2.16)

где

пл пл

∑

– среднее значение имитируемых экспертных оце-

нок пластового давления;

αα,1,

km kj

∑

– среднее значение имитируемых эксперт-

ных оценок фильтрационных параметров нефтяного пласта;

,1,

SSjm

∑

– среднее значение имитируемых эксперт-

ных оценок накопленной жидкости в скважине.

Для упрощенной модели (7.2.16) процедура определения фильтра-

ционных параметров содержит только три управляющих параметра и

имеет вид

11 1

1, 2, 3, αα α, ...,

jj j

−

−− −

=+Δ =

=A α B

(7.2.17)

где

1 1

зз пл пл

123

(()()β ()()ββ() ()) ,

TT T

PP P P S S

− −

=+ ++ADD DD Г DD

1 1

з з пл пл

123

(()()β ()()β () ()()) ,

PP Pе PSeS

− −

=+ +Δ+BDе D Гα βD

здесь

зз

(, ) (, )

( ( ) ( )) ( ( )( ), , 1, )

αα

Pt Pt

PP ijn

∂∂

∑

αα

DD – матрица част-

ных производных от функции

(, )

Pt α в моменты времени t

, 1, ;in=

()()

(

)

(

)

пл пл

,1,

αα

PT PT

PP ijm

⎛⎞

⎜⎟

⎝⎠

∂∂

αα

– матрица частных произ-

водных от функции

пл

(,α)PT ;

() ()

(

)

(

)

,1,

αα

ST ST

SS ijm

⎛

⎞

⎜

⎟

⎜

⎟

⎝

⎠

∂∂

Gα Gα

DD –

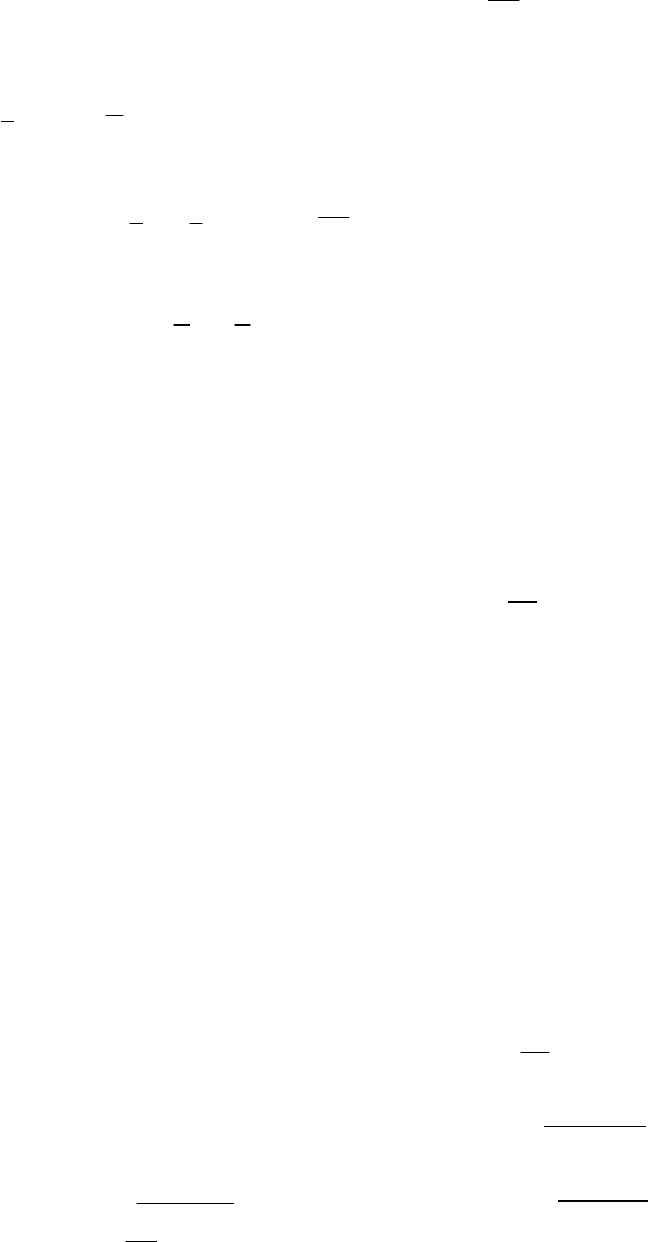
110

матрица, частных производных от функционала накопленной добычи

жидкости в скважине;

()

( )

зз з

(, , (), , 1,

iii

PPtPttqt in=− =e α) – вектор-

столбец невязок между измеренными значениями забойного давления и

соответствующими значениями забойного давления, полученными на

основе модели;

() ( )

( )

пл

пл пл

,eP P P T=− α

– невязка между средним зна-

чением экспертной оценки пластового давления и соответствующим

значением пластового давления, полученного к моменту времени T на

основе модели

пл

(, )PTα

;

((αα,1,))

inΔ= − =α

– вектор-столбец невя-

зок между средними экспертными значениями фильтрационных пара-

метров пласта и искомыми значениями фильтрационных параметров,

полученными на шаге 1

j − ;

( ) ( )

(, )eS S ST=− Gα

– невязка между сред-

ним значением экспертной оценки накопленной жидкости и значением

накопленной жидкости, полученным на основе модели (, )ST Gα ;

123

β , β , β

– управляющие параметры.

Приведем описание алгоритма синтеза оптимальных оценок пара-

метров упрощенной интегрированной системы моделей кривой восста-

новления забойного давления (КВД) (7.2.16), реализованного во втором

разделе процедуры Sub Example_2_В5а( ), приведенной в приложении

при заданных значениях управляющих параметров

β ,1,3

j = . В качест-

ве модели КВД использовалась функция вида(6.2.3):

зз

0213 00 223

(, , (,α ),α , α ) ( ) (1 exp( α )) α ln(α )Ptt qt Pt q t t= +−− ⋅ , (7.2.18)

где

()Pt – забойное давление в момент остановки скважины t

20 2

(,α )exp(α )qt q t=−

– дебит жидкости в скважине после ее остановки,

– дебит скважины до ее остановки,

α , α – параметры, характери-

зующие фильтрационные свойства нефтяного пласта.

Алгоритм синтеза оптимальных оценок параметров модели КВД

Алгоритм синтеза оптимальных параметров модели КВД с исполь-

зованием процедуры (7.2.17) представляет следующую последователь-

ность действий:

1. Задание начальных приближений параметров модели КВД

000

123

(α , α , α )=α , значений управляющих параметров β ,1,3

j = и вычис-

ление элементов матрицы частных производных

()PD

( )

Pt∂

∂

()

( )

023

1exp α ln α ,

qtt=−−

( )

()

( )

10 2 3

α exp α ln α

iii

qt t t

∂

=−

∂

()

Pt∂

∂

()

( )

10 2 3

α 1exp α / α , 1, .

qtin=−− =