Семиохин И.А., Страхов Б.В., Осипов А.И. Кинетика химических реакций

Подождите немного. Документ загружается.

Это выражение получило название потенциала Леннард-Джон-

са. Молекулярная- модель Ми — Леннард-Джонса характери-

зуется четырьмя независимыми параметрами (А>, а, т и л).

ЕСЛИ

дополнительно

учесть

другой

вид сил притяжения,

обусловленных взаимодействием диполей (ур.

6.40),

получим

более общее уравнение для потенциальной энергии взаимо-

действия

двух

частиц:

котором

2cos

cos

—sin

sin 6

cos

(ф

—\J>

(6.67)L

Предложенная модель Штокмайера характеризуется большим

числом независимых параметров.

Глава

ЭЛЕМЕНТЫ

КИНЕТИЧЕСКОЙ

ТЕОРИИ

ГАЗОВ

1. Распределение

молекул

по

энергетическим

состояниям.

Закон

Больцмана

Пусть рассматриваемая система состоит из N молекул, об-

ладает полной энергией U и имеет постоянный объем V. Тогда

с термодинамической точки зрения система изолирована

(t/=const,

V=const). Энергия Л

молекул распределена по

группам молекул таким образом, что

= const, (7.1>,

где Wг — число молекул с энергией e

Полное

число молекул также постоянно:

= N

+ N

+ ... = V.N|= const. (7.2)

Вероятность того, что система

будет

находиться в некото-

ром заданном состоянии, пропорциональна числу различимых

путей, которыми можно реализовать это состояние, т. е.

^ -Т^-. (7.3)

где Л/,! — число перестановок внутри группы молекул с

энер-

гией е,.

Равновесному состоянию изолированной системы отвечает

максимум энтропии

S, а со

статистической точки зрения

—

максимум термодинамической вероятности

Связь

между

5и

дает

формула Больцмана:

S =

klnW, (7.4)

которая

учетом

соотношения

(7.3)

преобразуется

форму

\. (7.5)

Поскольку

число молекул всегда очень велико

(~10

см~

при

нормальных условиях),

для

вычисления

N\ и Nil

можно

при-

менить известную формулу Стирлинга:

(7.6)

откуда

\nN\

= —

\n{2nN)

NlnN—N.

Для больших чисел In

N<^N

поэтому можно записать

lnNl

N\nN—N.

(7.7)

Выражение

для S/k

теперь

можно переписать в виде

S/k

NlnN—N-Y N

ИЛИ

Условие максимума энтропии

изолированной системе

сохраняется

для

всех

допустимых изменений переменных.

Найдем частные изменения энтропии:

dSi=

dNl=z

2+1} dN

Суммируя

вес

частные изменения энтропии, получим

ее

полное

изменение:

dS=—

откуда, очевидно,

£ (In

JV,+1)^=0.

(7.9)

Переменные

Ni не все независимы, они связаны между

собой

условиями

(7.1—7.2),

из которых следует, что

0. (7.10)

помощью последних уравнений можно выразить два значе-

ния dNi как функции всех остальных. Используем для этой

цели метод неопределенных множителей Лагранжа. Для этого

умножим соотношения

(7.10)

на к и у, соответственно и сло-

жим

их с уравнениями

(7.9).

Тогда получим

У.(1пЫ

к+ргд(Ш1

= 0.

(7.11)

Это

уравнение справедливо для произвольных значений dN

т.

е. когда каждая из скобок в сумме равна нулю. Следова-

тельно,

откуда

Ae'^

(7.12)

где

Чтобы

определить Л, сложим все числа молекул N

, опре-

деляемые соотношением

(7.12):

тогда

—

Л/ / V

Р""*

Ч\

Подставив

значение А в уравнение

(7.12),

получим

Прологарифмируем выражение

(7.14),

а затем умножим его

на Nr.

83-

Просуммировав все уравнения последнего типа, получим

Y^NtlnN^NlnN—

\iU—N

Чтобы найти \i, подставим в это уравнение из выражения (7.8)

значение S/k, тогда

S/k

= fit/ +

V е"

148

' ,

(7.15)

откуда

/-g-\

_2_

(7.16)

Из

термодинамики известно, что

TdS-pdV,

т. е.

/ ЯП \

Подставляя температуру в выражение (7.16), найдем, что

= -^г- (7.17)

Теперь уравнение

(7.12)

можно переписать в виде

Л^Ле-V"

(7.18)

Это

уравнение

дает

первую

формулировку

закона

Больцмана:

для молекулярной системы, находящейся в равновесии, число

молекул, обладающих энергией е/, пропорционально множите-

лю Больцмана е""~

//?г

. Из уравнений

(7.18)

(7.13)

можно

получить

другую

форму

закона

Больцмана:

А/

-е,/*Г

Ъ -

* /7 104

где сумма

£e-V*

(7.20)

называется молекулярной суммой по состояниям.

Если некоторые уровни обладают одинаковой энергией еь

выражение

(7.19)

приобретает вид

-zJkT

•^-

g<C

-e,

(7-21)

где gi — статистический вес или вырождение t-ro энергетиче-

ского уровня.

Распределение

молекул

идеального

газа

по

скоростям

поступательного

движения.

Закон

Максвелла—

Больцмана

Рассмотрим систему

из п

частиц

как

совокупность незави-

симых канонических систем, каждая

из

которых содержит

одну частицу.

применении

одной частице формула

(7.21)

означает вероятность

Р ее

нахождения

одном

из

состояний

с энергией

е.

Как

было показано

статистической термодинамике, одна

частица

фазовом пространстве занимает объем

Тогда

элементарном фазовом объеме

dxdydz

будет

содер-

жаться число состояний одной частицы, равное

dT =

dxdydz/h*.

(7.22)

Вероятность нахождения частицы идеального газа

элемен-

тарном объеме

с dT

состояниями

будет

равна

Ae~*'

dT.

(7.23)

Чтобы определить вероятность частицы иметь энергию

при

всевозможных значениях координат

импульсов, необходимо

проинтегрировать уравнение

(7.23)

по

всем импульсам

pxpyPz

при

условии

const

по

всем координатам.

Интегрирование

по

dxdydz

дает

объем

V, в

котором находится

частица.

Для

интегрирования

по

выразим сначала

энергию частицы

виде

mv*

mvi

mv\

(7.24)

где

px=mv

и т. д.

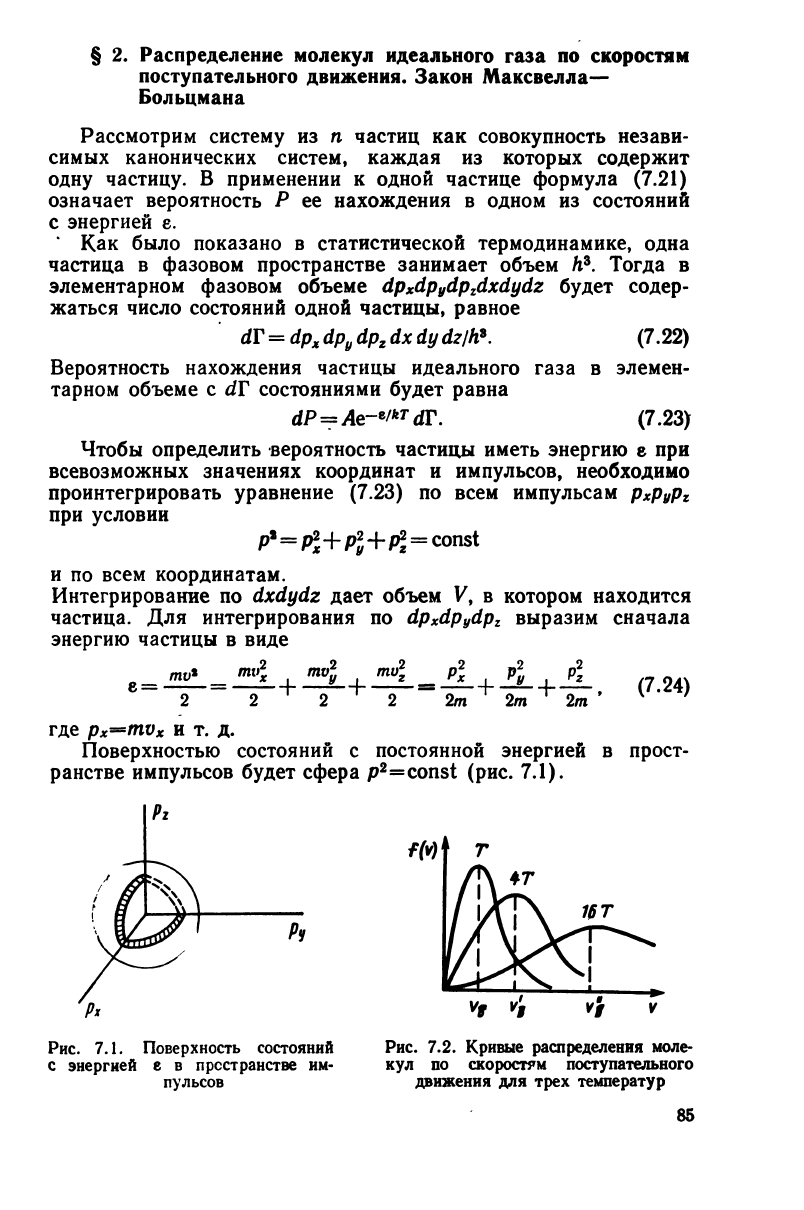
Поверхностью состояний

постоянной энергией

прост-

ранстве импульсов

будет

сфера p

=const (рис. 7.1).

Рг

Рис.

7.1. Поверхность состояний

энергией е в пространстве им-

пульсов

Рис.

7.2.

Кривые

распределения моле-

кул по скоростям поступательного

движения для трех температур

Интегрирование по шаровохму слою толщиною dp у поверх-

ности,

соответствующей энергии

е=р

/2т,

эквивалентно за-

мене:

Поэтому

вместо уравнения

(7.22)

можно записать

dl - - ,

(7.25>

где

v—p/m

— переменная скорость. Выражая и энергию е через

скорость v, перепишем уравнение

(7.23)

в виде

(v)

Здесь

dP(v)—вероятность того,

что

скорость частицы заклю-

чена между величинами

v и

v-rdv.

Постоянная

находится

из

условия нормировки:

U=oo

dP(iO=l.

(7.27>

Задача

сводится

вычислению интеграла:

ОО

Подобный

табличный интеграл вычисляется

по

формуле

l^-

>y*p.

(7.28)

Поэтому

—/V

Лв

J^.

(^-)

3/2

(7.29)

Из

условия

(7.27)

с учетом уравнений

(7.26)

(7.29)

полу-

чим

Уп

2kT \3/2_

\ m ) ~~

откуда

^^if^\

3/2

(7.30)

2kT

Подставляя

это значение А в уравнение

(7.26),

найдем, что

dP(t>)

= -^(-^)

8/2

e-»*/»V*.

(7.31)

Для

применения уравнения

(7.31)

к системе из п частиц

необходимо

использовать формулу сложения вероятностей,

считая каждую из частиц движущейся независимо и случайно,

что соответствует характеру движения частиц идеального газа.

Число

частиц, скорости которых заключены между v и v

dv,

равно

ndP(v),

относительное число частиц со скоростями между v и v

равно

*L&L

(^)

3/2

(7.32)

Эта

формула называется законом, распределения

Максвелла

—

Больцмана,

а величина

jiP (v) __

f ЛЛ

__ 4

/_^_\

3/2

-то«/2Л7*^,2

(7.33)

по определению есть функция распределения частиц по скоро-

стям

поступательного движения. На рис. 7.2 представлена за-

висимость функции распределения f(v) от v, Т. е. зависимость

от

v доли молекул, скорости которых заключены между v и

dv.

Как видно из рисунка, с увеличением температуры макси-

мум распределения смещается в сторону больших скоростей,

высота

кривой

в максимуме несколько понижается. Наличие

максимума объясняется двумя противодействующими

причи-

нами: вероятность состояний с ростом скорости падает, а плот-

ность состояний, наоборот, увеличивается.

Среднее

значение функций q>(v) вычисляется по формуле

для среднего:

(7.34)

Поэтому

^У^=

Y^f-

35)

<v)=

Скорость v

отвечающая максимуму кривой, называется наи-

более

вероятной. Она находится из условия экстремума:

равна

Сравнивая формулы

(7.35)

(7.36),

находим,

что

YW)

\Af-

(Р)

"/т

37>

сами эти скорости относятся одна

другой

как

YW)

'•

(v) :

и*

= 1.224

1,128

1,000.

(7.38>

Кинематические характеристики молекулярного

движения

Эффективное сечение столкновений. Средняя длина

сво-

бодного

пробега.

При

столкновении частицы

молекулой

по-

следняя

может либо

упруго

рассеяться, либо передать часть

энергии

во

внутренние

виды

движения.

любом случае

ре-

зультат столкновения может быть оценен некоторой вероят-

ностью,

которая пропорциональна сечению столкновения.

Пусть

налетающая частица считается точечной,

мишень

имеет

геометрические размеры, соответствующие площади

се-

чения о. Эта площадь определяется по-

тенциалом межмолекулярного взаимо-

действия

подбирается таким обра-

зом,

чтобы вероятность какого-то

ре-

зультата столкновения была равна ве-

роятности того,

что

налегающая

час-

тица, двигаясь прямо без взаимодейст-

вия, попадает

площадку о. Пусть

на-

летающая частица попадает

на пло-

щадь

объема,

котором расположе-

ны частицы-мишени

концентрацией

тг

см~

(рис. 7.3).

слое

толщиной

Рис. 7.3.

К определению пло-

нахО

пится

rirSdx

мишеней

РУММЯ

по-

щади поперечного сечения находится п^ах мишеней, сумма по-

перечных сечении которых

равна

Вероятность

попадания налетающей частицы

одну

из

мише-

ней равна

dP=

—

Вероятность

события растет пропорционально пути, проходи-,

мому налетающей частицей,

будет равна единице

на

пути

</>,

называемом

средней

длиной

свободного

пробега:

(1)=1/оп

(7.39>

Поперечное

сечение столкновений определяют эксперимен-

тально

по

уменьшению интенсивности (плотности) потока

па-

дающих

частиц

1(х) по

мере прохождения

х в

некоторрм газе

или

другой среде. Ослабление потока налетающих частиц

бу-

дет равно

(х)=—1

(х)

dP=—I

(x)

апо

dx.

АО)

Знак

минус указывает

на

убыль плотности потока

ростом

х.

Интегрируя выражение (7.40)

от 0 до х,

получим

/(х) = /(0)е^*, (7.41)

откуда можно получить выражение

для

поперечного сечения

столкновений:

1Г^Ш

.42)

Если падающая частица движется

со

средней скоростью

<v>,

то она

пройдет длину свободного пробега

за

время

*=</>/<*).

(7.43)

Средняя

частота столкновений налетающей частицы (число

столкновений

в 1

сек)

будет

равна

(7.44)

Частота

столкновений

системе

упругих

шаров.

Пусть

налетающая частица имеет некоторую массу

т и

радиус

равные массе

радиусу неподвижных мишеней,

движется

со скоростью

<v>.

Тогда

на

любом пройденном расстоянии

налетающая частица столкнется

со

всеми мишенями

цилинд-

ре радиусом

2г

(рис. 7.4).

Рис.

7.4. Площадь поперечного сече- Рис. 7.5. К вычислению относительной

ния упругих шаров скорости

Средняя

длина свободного пробега

будет

равна

</>

А.

(7.45)

ап

*лг1п

а частота соударений между молекулами соответственно

v' = вп

(v) = 4лг

(v). (7.46)

В действительности

газе движутся

не

только налетающие

частицы,

но и

мишени, причем

их

скорости задаются распре-

делением Максвелла—Больцмана. В таком случае под ско-

ростью

<У>

в уравнении

(7.46)

понимают уже относительную

скорость, равную

VOTH

= V

— V

Абсолютное значение

0TB

вычисляется по формуле

1'отн

= V

"(vi-v

)

= Vv\+v\-2v

cos

6, (7.47)

где

— угол между векторами скоростей Vi и v

(рис. 7.5).

Среднее

значение относительной скорости надо

вычислять

учетом распределения Максвелла — Больцмана [уравнение

(7.32)].

С этой целью направим ось z сферической системы

координат по вектору v

тогда получим

2Я Я оо

откуда

<tw> =/2

{v)

j/-^-.

(7.48)

учетом распределения Максвелла — Больцмана выражения

для v' и </> принимают вид

v' -

nrlno

(v)

16гЯ

[/^

(7.49)

где

[

SRT

Для

нормальных условий в воздухе имеем /г

~1О

см~

Го-^Ю"

см,

<0>~5«1О

см/с, поэтому

</>^10~

см и v'~

—10

с-

При

р=1 мм рт. ст.

</>~10-

см, а при

р=10~

мм рт. ст.

</>~1

см.

Для

частиц двух сортов с молекулярными массами М

частота столкновений частицы (М

{

) с частицами (М

) в

см

будет равна