Семиохин И.А., Страхов Б.В., Осипов А.И. Кинетика химических реакций
Подождите немного. Документ загружается.


Рис.
5.2. Зависимость п
ОА
х от
—«о A
In (1-х) для необратимой ре-
акции
первого порядка в режиме иде-
ального вытеснения
Рис.
Л
ОА*
5.3.
х
1-Х
Зависимость
п
ОА
х от
для
необратимой реакции
1-х
первого порядка в режиме идеального
перемешивания
Если
в
реакции образуется лишь один продукт
А-*А',
(5.36)
то а=1,
р=0 и
уравнение
(5.32)
значительно упрощается:
RT
где /io
A
—
= v
—
объем газа, проходящего
в
единицу времени
р
через сечение реактора; V — объем реактора.
Так
как
V/v
= t,
(5.38)
приходим
к
простому виду уравнения
для
константы скорости
реакции
в
потоке
(в
режиме идеального вытеснения):
<5.39>
совпадающему
с
уравнением необратимой реакции первого
по-
рядка
в
замкнутой системе.
Это и
понятно, поскольку реакция
(5.36)
в
потоке происходит при сохранении реагирующей систе-
мой
постоянного объема,
что
наблюдается при сохранении чис-
ла молей
в
газовой фазе.
§
4. Кинетика реакций в режиме идеального
перемешивания
Если
в
реактор, объем которого
V
изменяется, вводят смесь
веществ
с
объемной скоростью
v
x
и отбирают
ее с
объемной ско-
ростью v
2
y то
в
соответствии
с
уравнением материального балан-
6L

•са
изменение числа молей вещества А,-
в
единицу времени
в
реак-
торе
равно
d(c
k
V)
—%—=c
OA(Vl
-c
Ai
v
%
-wV.
1(5.40)
В
этом уравнении
w
— истинная скорость химической реак-
ции; c
0Ai
—концентрация вещества
А/ на
входе
в
реактор:
;
(5.41)
с\*—
концентрация этого вещества
на
©ыходе
из
реактора:
CA^n
Al
lv
%
.
(5.42)
В
режиме идеального перемешивания
она
равна концентра-
ции
А в
любой точке
внутри
реактора. Значения
п
0А(
и n
Ai
соответствуют
числам молей вещества
А,,
поступающего
в
реактор
и
выходящего
из
него
в
единицу времени.
Если
реакция происходит
в
газовой
фазе,
то газ
будет
за-
нимать весь объем реактора
V и
выражение
(5.40)
можно
записать
в
виде
^
(5.43)
откуда
.-JU—4
£..
,6.44»
В
стационарном состоянии
в
реакторе идеального переме-
шивания концентрация
с
А(
любого вещества
A
t
перестает зави-
сеть
от
времени,
в
связи
с чем
уравнение
(5.44)
упрощается:
с
АА
v
x
—c
k
v
2
п
ЛА
—л.
w=
0Ai
±LL=-!h ^L
(5.45)
V
V
У
'
Запишем
для n
Ai
, как и
ранее
(5.15),
соотношение
и
с его
учетом перепишем уравнение
(5.45):
w=
^ .
(5.46)
В
общем случае
в
соответствии
с
основным постулатом
хи-
мической кинетики
для
необратимых
и
обратимых реакций
разных порядков имеем
у A
t
A
t
* *
*
62
(5.47)

и
соответственно
L_
=
kc
v
*с)*
... —k'c
X
'C ?...
.
(5.48)
Сопоставляя
полученные выражения
с
соотношениями
(5.17)
и
(5.18), находим,
что для
режима идеального переме-
шивания
скорость реакции записывается
в
виде алгебраиче-
ских уравнений,
тогда
как для
режима идеального вытеснения
она
представляется
в
виде дифференциальных уравнений.
§
5. Кинетическое уравнение необратимой реакции первого
порядка
в режиме идеального перемешивания
Рассмотрим простейшую реакцию типа
A->v
1
A
1
+v
2
A
a
+
Скорость
такой реакции
в
режиме идеального перемешивания
может быть записана
в
виде
^
*X-^,
(5-49)
где
у
а
=
2п—,
(5.50)
Р
2п=п
ОА
(1
+
$х)
и
п
А
=
л
0А
(1 — х).
Подставим значения
n
A
, v
2y
2n из
последних
трех
соотноше-
ний
в
уравнение
(5.49)
и
получим выражение
(5.51)
v
7
V
1
+
р*
RT
f
откуда
МУ
(
'
+ М
£
(5.52)
1
(1-*)У
Р
Для определения константы скорости
k
x
преобразуем уравне-
ние
(5.52)
в
другую
форму
и
добавим
в
скобки чистителя
справа
Q
. и —р.*
^^ (5-53)
Разделив
это
уравнение
на р,
запишем
его в
следующей форме:
Теперь, если
в
качестве переменных взять
63

то
получим уравнение прямой линии
изображенной
на рис. 5.3. Тангенс угла наклона прямой по-
зволяет
определить (}:
tg(p=
"T
i
*
(5
-
55)
а
отрезок, отсекаемый прямой на оси ординат, — значение Ё\:\
0A
-jw-
(5
-
56
>
Если
протекает реакция типа
то {$=0
и уравнение
(5.52)
упрощается:
-x)
p
(557)
Выразим объем выходящего из реактора газа с помощью со-
отношения
v
2
= = п
0А
(5.58)
Р
Р
и, учитывая, что V/v
2
=t, получим из уравнения
(5.57)
выра-
жение
(5.59)
Из
этого выражения видно, что доля реагирующего вещества
в реакторе идеального перемешивания в случае простейшей
реакции описывается зависимостью
*-т&-
(560)
представляющую
собой
кривую
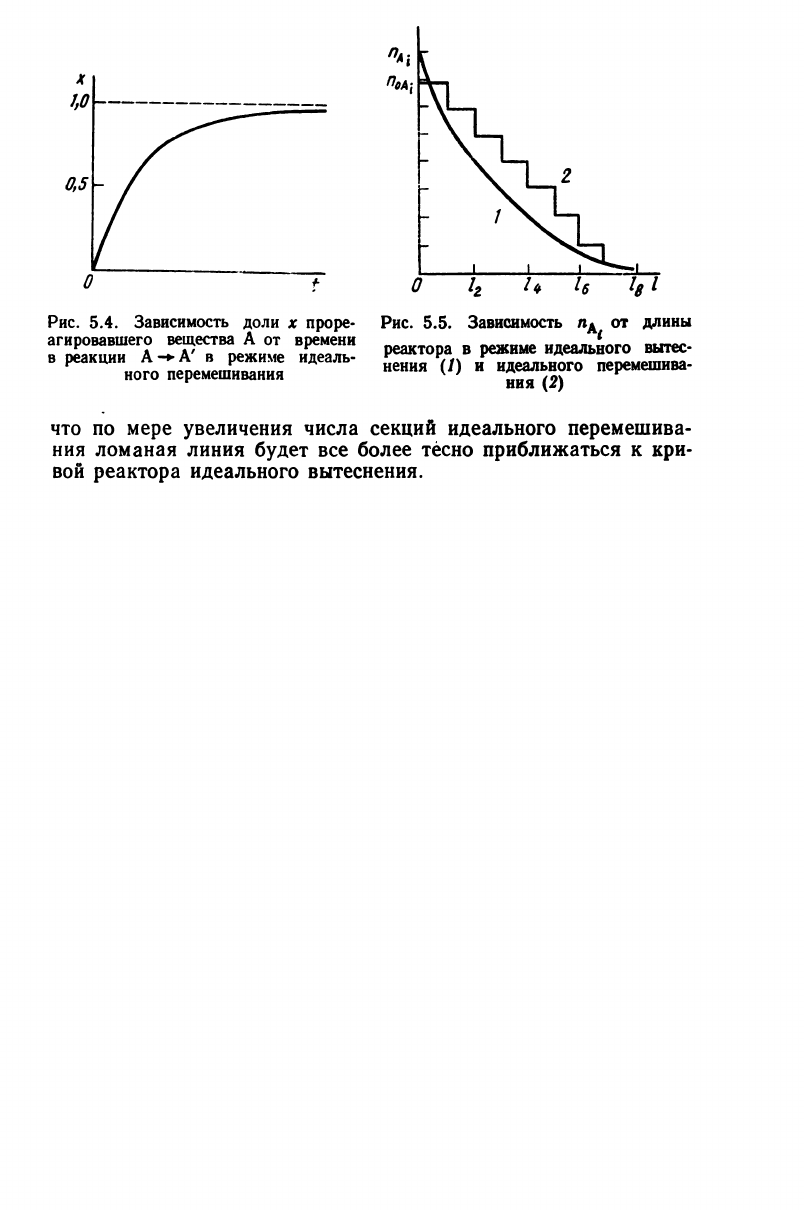
с насыщением (рис. 5.4).
При
последовательном соединении небольшого числа (—10)
реакторов идеального перемешивания система начинает вести
себя
как один реактор идеального вытеснения. Изобразим на
рис.
5.5 зависимость ПА, ОТ длины реактора при идеальном
вытеснении (кривая 1) и идеальном перемешивании в реак-
торе,
разделенном на секции одинаковой длины /
(
(ломаная
линия 2). Тогда, при одинаковых скоростях подачи реагирую-
щих
веществ и температуре в реакторах, получим наряду с
кривой / для реакторов идеального вытеснения ломаную ли-
нию 2 для реакторов идеального перемешивания. Очевидно,
X
hO
о
/•
h
I
Рис.
5.4. Зависимость доли х проре- Рис. 5.5. Зависимость п
А
от
длины
9ГиППП9Ш1№ГЛ
ПР1ПР/*ТПЯ
А ОТ
ПТДОМРиЫ
'
реактора в режиме идеального вытес-
нения (/) и идеального перемешива-
ния (2)
в реакции А-*А в режиме идеаль-
ного перемешивания
что по мере увеличения числа секций идеального перемешива-
ния ломаная линия
будет
все
более
тесно
приближаться к кри-
вой реактора идеального вытеснения.

Раздел
II
ОСНОВЫ
ТЕОРИИ
ХИМИЧЕСКОЙ
КИНЕТИКИ
Глава
6
ДИНАМИКА
ДВОЙНОГО
СТОЛКНОВЕНИЯ
§
1.
Классификация
реакций
в
химической
кинетике
При
исследовании кинетики химических реакций
их
клас-
сифицируют
по
ряду признаков. Одним
из
таких признаков
является
степень
отклонения
системы
от
равновесия.
Ясно, что
в равновесной системе химические реакции
не
идут
(точнее
идут,
но с
одинаковой скоростью
в
прямом
и
обратном
на-
правлениях, так что
в
системе
не
наблюдается никакого
из-
менения).
Вблизи
от
равновесия можно выделить несколько случаев.
1. Процессы переноса (обмен энергией, диффузия
и
другие
процессы переноса)
идут
быстрее, чем химические превраще-
ния.
В
таких системах
отсутствуют
градиенты температур
и
концентраций.
Для их
математического описания использу-
ются уравнения феноменологической кинетики.
2. Химические превращения происходят быстрее,
чем со-
путствующие им процессы переноса. Общая скорость химиче-
ского превращения
в
этом
случае
определяется скоростями
процессов переноса.
3. Скорости химических реакций сопоставимы
со
скоростя-
ми процессов переноса. Для описания кинетики таких процес-
сов необходимо совместное решение кинетических уравнений
химических реакций и уравнений переноса.
Вторым признаком,
по
которому удобно классифицировать
реакции,
является
величина
энергии
активации. Как известно,
многие бимолекулярные реакции
в
газах
и
растворах
идут
медленно,
так
как обладают высокими значениями энергии
активации:
E
a
*>RT.
Температурная зависимость скорости
та-
ких реакций хорошо передается уравнением Аррениуса:
k(T)=A(T)e~
E
«
/RT
t
(6.1)
где
А(Т)~Т
п
.
Быстрые реакции наблюдаются при малых значениях
энер-
гии активации: £
а
</?7\
В
этих случаях зависимость
k(T)^A(T)~T
n
(6.2)
аналогична зависимости коэффициентов переноса (А,, г\
и D)
от температуры.
66

В промежуточной области, когда
E>RT
t
конкурируют оба
сомножителя в уравнении (6.1) и зависимость k от Т имеет
сложный характер. Так, если Е
а
~0, скорость реакции может
уменьшаться с ростом температуры, что наблюдается, напри-
мер, в ряде тримолекулярных реакций
(2NO+O
2
,
2NO +
C1
2
,
тройная рекомбинация атомов или радикалов и т. п.), когда
в уравнении (6.2) п<0.
В бимолекулярных реакциях взаимодействия ионов с мо-
лекулами константа скорости реакции часто не зависит от тем-
пературы:
fc
=
const^/(7y (6.3)
В основу
третьего
типа классификации химических реак-
ций
положен такой признак, как
степень
отклонения
системы
от
однородности.
Здесь возможны случаи, когда система про-
странственно однородна, но изменяется во времени. Такая си-
стема совпадает со
случаем
1 первой классификации. Если же
система пространственно неоднородна, но стационарна, то
кине-
тика протекающих в ней реакций описывается уравнениями
химических реакций в потоке. Случай, когда система прост-
ранственно неоднородна и изменяется во времени, аналогичен
случаю
3 первой классификации.
Быстрые реакции, происходящие в условиях кинетической
неравновесности системы по отношению ко многим физиче-
ским
свойствам, включая и энергетические распределения ча-
стиц по разным степеням свободы,
требуют
учета
изменения
функций
распределения в
ходе
реакций.
Для вычисления применяемых в химической кинетике ста-
тистических (макроскопических) констант скорости реакций
в общем
случае
(для кинетически равновесных и неравновес-
ных систем) необходимо установить связь
между
этими кон-
стантами и молекулярными параметрами отдельных столкно-
вений.
§
2.
Типы
двойных
столкновений
Химические реакции происходят при столкновениях реаги-
рующих
веществ. Однако не все возможные столкновения при-
водят к химическим реакциям. Рассмотрим три типа столкно-
вений
(элементарных актов)
между
частицами А и В с задан-
ными
начальными скоростями движения v
A
и v
B
и наборами
внутренних квантовых чисел / и / соответственно.
1.
Упругие
столкновения
происходят с изменением скоро-
стей движения частиц А и В до значений Уд и v^ и рассея-
нием
их на некоторые
углы
8:
А(/, v
A
) + B(/,
v
B
)->A(*\
v'
A
) + B(j
9
vj,). (6.4)
3*
67

2.
Неупругие
столкновения
происходят
с
изменением
ско-
ростей
и
внутренних квантовых чисел частиц
А и В:
/, v;)+B(m
f
v^. (6.5)
Такие
столкновения приводят
к
обмену энергией
между
раз-
личными
степенями свободы.
3.
Химические
столкновения
(реакции) происходят
с
пере-
распределением атомов
между
молекулами
и
образованием
новых частиц
С и D:
А(*\ Ул)
+
В(/,
v
B
)-*C(/,
v
c
)+D(m,
v
D
). (6.6)
К
химическим реакциям, естественно, относятся
и
реакции
изомеризации,
которые происходят также
в
результате
двой-
ных столкновений
и
которые
могут
быть описаны схемой (6.6).
В последующих параграфах данной главы
и в
следующих
двух
главах
авторы намерены описать различные типы столк-
новений
с
учетом
молекулярных моделей
и
функций распре-
деления,
необходимых
для
определения таких кинематических
характеристик,
как
сечение столкновения
и
средняя длина
сво-
бодного пробега.
Эти
величины являются обычно предметом
исследования молекулярной
физики,
однако
нам
казалось
по-
лезным использовать
их
непосредственно
в
химической
кине-
тике
для
расчета основных характеристик, таких
как кон-
станта скорости реакции
и
коэффициенты переноса.
§
3. Упругое центральное столкновение
Рассмотрим столкновение жестких шаров
по
линии, соеди-
няющей
их
центры. Если точечная частица
с
массой
гп\ и на-
чальной скоростью
V\a
столкнется
с
неподвижной частицей
с
массой
т
2
, то в
результате
столкновения скорость первой
ча-
стицы уменьшится
до
величины
v
xp
, а
вторая частица приобре-
тет скорость
t;
2
.
Из
законов сохранения энергии
и
импульса получим
2
И
m
i
v
ia
== m
iVip
~f~
m
%
v
2
. (6.8)
Подставив значение
v
2
из уравнения (6.8)
в
уравнение
(6.7),
находим
(6.8а)
nit
68

Сокращая
левую
и
правую части последнего уравнения
на
ГП\ И (V\
a
—V\
p
), ПОЛУЧИМ
= —
откуда
ia
. (6.10)
В
случае
упругого
столкновения налетающего электрона
с
атомом имеем,
в
соответствии
с
уравнениями
(6.10)
и
(6.9),
т
х
<
m
2
,
v
t
=
^^ v
u
(6.10а>
Следовательно, электрон практически сохраняет свою скорость»
но
меняет направление движения.
Если
же
сталкиваются частицы примерно равных масс,
то
скорость налетающей частицы практически уменьшается
да
нуля:
flip—
0,
а мишень приобретает скорость
и
направление движения,
оди-
наковые
с
начальной скоростью ударяющей частицы:
v
2
~v
la
.
(6.10б>
Кинетическая
энергия электрона, передаваемая тяжелой
частице
с
массой
т
2
,
составляет при упругом
ударе
или
с
учетом соотношения
(6.10а)
Переданная
энергия составляет малую долю
от
начальной
ки-
нетической
энергии электрона
е
0
, а
именно
т
г
2 ' 2 т
%
69

Таким образом, кинетическая энергия, передаваемая элект-
роном тяжелой частице при
упругом
соударении, составляет
е
2
=
4-^-е
0
.
(6.11)
Это
означает, что
даже
при столкновении с
легкими
атомами,
такими как атом гелия, электрон может передать им только
0,05%
своей начальной энергии. При столкновении с тяжелыми
атомами, такими как атомы ртути, доля передаваемой элект-
роном энергии равна всего
0,001%.
Аналогично
можно показать, что энергия, приобретаемая
электронами (т
2
) при соударении с тяжелыми налетающими
частицами (mi), составляет
е
эл
=4^-е
0
,
(6.12)
где
ео
— начальная кинетическая энергия налетающей частицы
с
массой т
х
. Из уравнения
(6.12)
следует, что
даже
протон
(элементарная
частица) может передать электрону при
упру-
гом соударении
лишь
0,22% своей начальной энергии.
§
4. Неупругое центральное столкновение
Допустим
для простоты рассмотрения, что частицы не под-
вержены действию никаких внешних полей, кроме полей самих
частиц. В этом случае, если часть энергии налетающей час-
тицы
т
х
превращается во внутреннюю энергию 6 мишени т
2
,
можно
записать по аналогии с уравнением (6.7)
Определим,
при каких условиях получится бмаке. Для этого
подставим из уравнения (6.8) в уравнение
(6.13)
значение v
2
:
2
«1»?,
"=
«!»?„+
—
(fla-"lp)
2
+ 26
(6.14)
и
продифференцируем
это
соотношение
по v
]p
,
считая
v
{a
по-
стоянной
величиной.
Найдем,
что
2
—
—
(v
la
—^
**
dv
lp
откуда
db
du
lp
m
2
70
ml
—
(Vi
a
-v
u
)-
