Семиохин И.А., Страхов Б.В., Осипов А.И. Кинетика химических реакций

Подождите немного. Документ загружается.

начает, что

кривая

зависимости y(t) имеет перегиб. Используя

необходимое

условие перегиба и уравнение

(3.25),

запишем

т.

е. d

z/dt

обращается в

нуль

при том же значении t, что и

производная

dy/dt.

Следовательно,

'пер — Гмакс 7 7 Г"^ 77' ^ '

Рассмотрим

предел *макс=*пер при

|-*<х>.

Чтобы разрешить не-

определенность

оо/оо,

воспользуемся правилом Лопиталя:

lim

MaKC

=lim—!5£—

= lim

-^-=0.

(3.32)

l-oo

S-*oo^(g—

1) ^oo k

Таким образом, максимум концентрации промежуточного

вещества В с возрастанием

/ki

не только уменьшается, как

было показано

выше,

но и смещается к началу координат.

Очевидно, что по мере увеличения отношения констант

кривая

y(t)

приближается к оси абсцисс и производная

dy/dt

все боль-

ше приближается к нулю.

При

k^>k

уравнение

(3.27)

можно заменить следующим

выражением:

Запишем отношение

[В]/[А],

учитывая

(3.26):

Т1

)

(3.33)

[А]

X k

1/2(1)

где

т./,(1)

т./,(2)

— периоды полупревращения веществ А и В,

Выражение

(3.33)

получило название векового равновесия.

При

уравнение

(3.27)

приобретает вид

этом случае отношение

[В]/[А]

становится

равным:

i5L

JL=:_^_

(3.33а)

[А]

кг-к

Это

уравнение отвечает постоянству отношения концентраций

промежуточного вещества В и исходного вещества А в стацио-

нарном состоянии. В отличие от предыдущего векового равно-

весия последнее состояние

(3.33а)

называют переходным рав-

новесием,.

5. Механизм сложных реакций. Принцип стационарных

концентраций

Одной

из

типичных

задач феноменологической кинетики яв-

ляется

установление кинетического уравнения сложной реак-

ции на основе ее механизма. При решении этой задачи исполь-

зуют

основной постулат химической кинетики,

принцип

неза-

висимости и

принцип

стационарных концентраций.

Пусть

реакция типа

идет

по сложному механизму с образованием двух промежу-

точных веществ

М.

{

и М

A-^

B-b-C

+Mt

(3.34)

+A-*-*C+M

Mi-fMx-^A.

Пользуясь

основным постулатом химической кинетики

(1.11а)

уравнением

(1.10),

запишем уравнения для скоростей эле-

ментарных стадий:

35)

dt dt

Используя

эти соотношения, запишем теперь уравнения для

суммарных скоростей изменения концентраций исходных ве-

ществ,

промежуточных веществ и продуктов реакции:

-к

[MJ

[В]

]

[А]-2Л

[Щ\

(3.36)

Получили систему пяти нелинейных дифференциальных

уравнений с постоянными.коэффициентами. В качестве началь-

ных условий взяты уравнения материального баланса:

(3-37)

Эта система не интегрируется в квадратурах. Ее решение мож-

но

проводить с помощью численных методов (в том числе с

использованием ЭВМ) или применять какие-либо приближен-

ные

методы (чаще всего это принцип стационарных концент-

раций).

Допустим, что концентрации промежуточных веществ малы

по

сравнению с концентрациями исходных веществ и продук-

тов реакции. В этом случае вместо условий (3.37) запишем

Дифференцируя эти уравнения по времени

<*[А] • 1 d[C] _

Q и

d[B] I d[C) _

dt 2 dt dt 2 dt

подставляя соответствующие значения скоростей из (3.36),

получим

ИЛИ

Аналогично,

-М

Мх]

[В]

+ у

*,[

[Bj + ± k

[м

]

[А]=о,

или,

что то же самое,

Из

этого следует, что при условии

[MJ, [М

]<[А], [В], [С] (3.38)

концентрации

промежуточных веществ стационарны, т. е.

AML^o,

IM«]

=0 (

3.з9)

dt dt

v ;

Соотношения

(3.39) и являются выражением

принципа

ста-

ционарных

концентраций,

а неравенство (3.38) — достаточным

2 Зак 303 33

условием

корректного его применения. Принцип стационарных

концентраций следует применять в случае, когда промежуточ-

ные вещества обладают высокой реакционной активностью и в

силу

этого не накапливаются в

ходе

реакции.

Производные

по времени от концентраций реагирующих ве-

ществ

равны

нулю и тогда, когда значения концентраций экс-

тремальны, но в этом случае — только в точке экстремума

или с учетом ошибок кинетических измерений — в некоторой

ее

окрестности. В литературе иногда принимаются за стацио-

нарные концентрации промежуточных веществ, далекие от ну-

левых. Однако в

этих

случаях желательно экспериментальное

подтверждение

справедливости сделанного предположения.

Вернемся

к системе уравнений

(3.36).

Складывая два пред-

последних

уравнения

этой

системы и учитывая соотношения

(3.39),

найдем концентрации промежуточных веществ М, и М

Подставив

эти значения в уравнение для скорости

образо-

вания продукта реакции

(3.36):

обозначая концентрацию С через 2х, получим

[А]

[А]„-х,

[В]

-х

^Н

1/2

^-х).

(3.40)

Таким образом, в результате применения принципа стационар-

ных концентраций для скорости реакции получено дифферен-

циальное уравнение с разделяющимися переменными, которое

нетрудно

проинтегрировать. Следует отметить, что в уравнении

(3.40)

отсутствует константа

k$,

т. е. скорость реакции не за-

висит от ее величины.

качестве второго примера рассмотрим механизм

образо-

вания бромистого водорода:

Вг

->-2НВг.

интервале температур от 230 до

300

°С эта реакция, по Бо-

денштейну, происходит по

схеме:

Вг+Н

->НВг

Н,

ДН

69,9

кДж/моль;

Вг

->НВг

Вг,

ДН

—172,0

кДж/моль;

(3.41)

НВг-*Н

+Вг,

ДН

=—69,9

кДж/моль;

Из-за

сильной эндотермичности

этой

схеме

не

учитывается

стадия Вг+НВг-*Н + Вг

Скорость образования бромистого водорода можно записать

в виде

(3.42)

Согласно принципу стационарных концентраций Боденштей-

на

для

промежуточных веществ (атомов

Н и Вг):

[Вг

]

[H]

[HBr]—2k

[Br]

[M]

(3.43)

Складывая

оба

уравнения, получим

1/2

. (3.44)

Подставим теперь значение

[Вг] в

первое

уравнение системы

(3.43):

= MHtHMBr,]/*,,)"

3 45

ftj,[Brt)+ft«[HBr]

" '

При

совместном решении уравнений

(3.42)

(3.43)

получим

соотношение

для

скорости образования бромистого водорода:

, (3.46)

Подставим

в это

соотношение значение

[HI из

(3.45):

I d

[HBr]

frfr

[Hl

]

[Вг

]

dt ЫВг

]+*

[НВг]

Разделив числитель

знаменатель

на

ЫВг

], получим выраже-

ние

для

скорости образования бромистого врдорода

соответ-

ствии

рассмотренным выше механизмом реакции:

MW^N^

47)

+ Л1НВг]/Л[Вг] '

Это выражение совпадает

приведенным

в § 5

главы

1 ки-

нетическим уравнением, полученным

из

опытных данных.

Применение

принципа стационарных концентраций, приво-

дящее

замене части дифференциальных уравнений алгебраи-

ческими, позволяет получать кинетические уравнения сложных

реакций

аналитическом виде. Однако

при

таком

подходе

уравнения становятся приближенными, происходит неизбежная

потеря информации.

Чтобы

получить представление о характере приближений,

обратимся

к простейшему примеру — последовательным реак-

циям первого порядка, рассмотренным в § 4 настоящей

главы:

Интегрируя систему кинетических уравнений

(3.26—3.28),

мы получили

a(1

где

х, у, z — текущие концентрации веществ А, В и С соответ-

ственно.

Применяя

принцип стационарных концентраций к концент-

рации вещества В, предположим, что

dy/dt=O,

тогда

Сравнивая приближенное решение с точным, обратим вни-

мание на то, что концентрация продукта реакции z не зависит

от

константы скорости k

и целиком определяется только кон-

стантой

скорости первой реакции k

. С другой стороны, при

{

концентрации А и В в любой момент времени равны.

Если

же

то концентрация В при /-*0 стремится к вели-

чине, превышающей начальную концентрацию А. Таким обра-

зом,

принцип стационарных концентраций нельзя применять

при значениях констант скорости

>>k

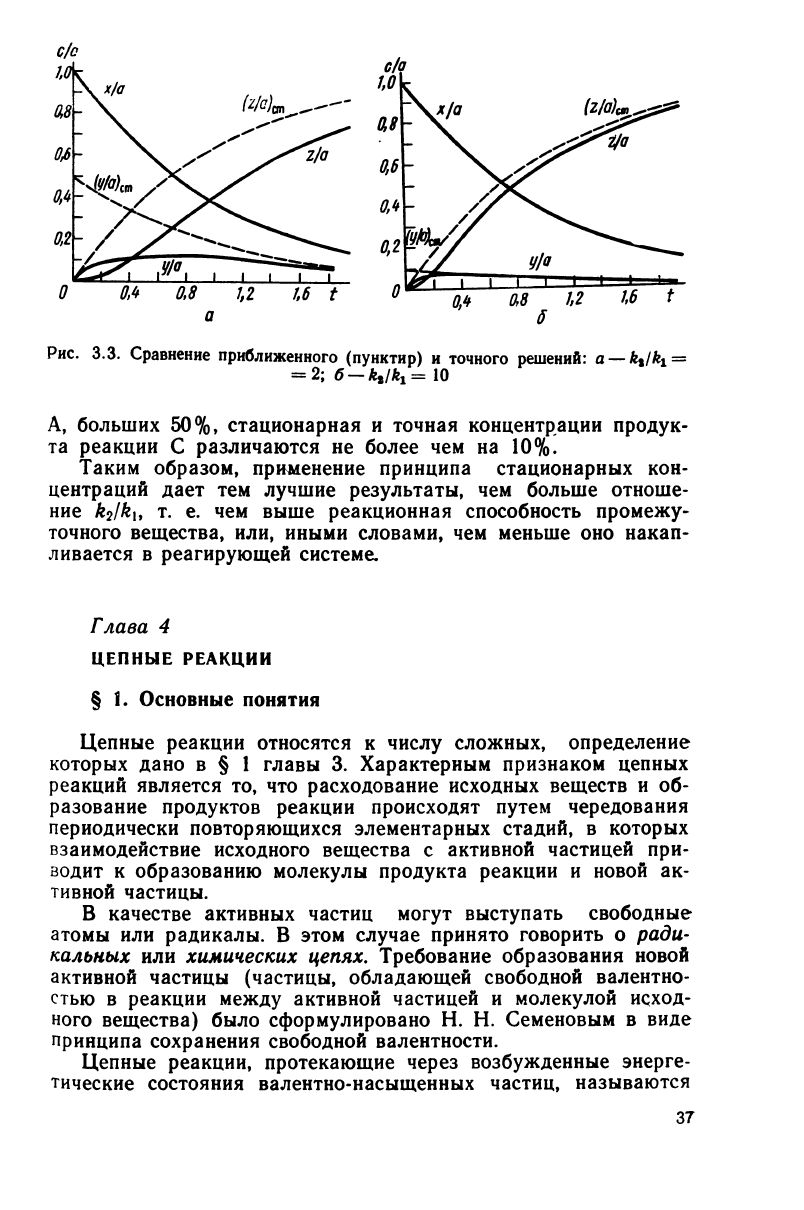
Для выяснения роли

отношения

констант k

\k\ рассмотрим два примера (рис.

3.3,

а, б).

первом случае

{

=2)

концентрация промежуточного

вещества

В, рассчитанная с применением принципа стационар-

ных концентраций, становится близкой к соответствующей кон-

центрации, полученной из точного решения

лишь

тогда, когда

степень

превращения исходного вещества достигла 70%- К это-

му же времени стационарная концентрация продукта реакции

отличается от точно вычисленной на 50% ее> величины.

Во

втором случае

{

=l0)

стационарная концентрация

промежуточного вещества В практически совпадает с вычис-

ленной из точного решения, начиная со степени превращения

исходного

вещества, равной 20%. При степенях превращения

0,4

0,8 1,2 1,6 t

Ofi

0,8 1,2

Рис.

3.3. Сравнение приближенного (пунктир) и точного решений:

—

1,6

А, больших 50%, стационарная и точная концентрации продук-

та

реакции С различаются не

более

чем на 10%.

Таким образом, применение

принципа

стационарных кон-

центраций

дает

тем

лучшие

результаты, чем больше отноше-

ние

т. е. чем

выше

реакционная способность промежу-

точного вещества, или,

иными

словами, чем меньше оно накап-

ливается в реагирующей системе.

Глава

ЦЕПНЫЕ РЕАКЦИИ

Основные понятия

Цепные

реакции относятся к числу сложных, определение

которых дано в § 1

главы

3. Характерным признаком цепных

реакций является то, что расходование исходных веществ и об-

разование продуктов реакции происходят путем чередования

периодически повторяющихся элементарных стадий, в которых

взаимодействие исходного вещества с активной частицей при-

водит к образованию молекулы продукта реакции и новой ак-

тивной частицы.

качестве активных частиц могут выступать свободные

атомы или радикалы. В этом случае принято говорить о ради-

кальных

или химических цепях. Требование образования новой

активной частицы (частицы, обладающей свободной валентно-

стью в реакции между активной частицей и молекулой

исход-

ного вещества) было сформулировано Н. Н. Семеновым в виде

принципа

сохранения свободной валентности.

Цепные

реакции, протекающие через возбужденные энерге-

тические состояния валентно-насыщенных частиц, называются

реакциями с энергетическими цепями. Широко распростране-

ны смешанные цепи, в которых участвуют активные частицы

того

и другого сорта.

Образование

продуктов реакции при взаимодействии актив-

ных частиц с молекулами исходного вещества не является до-

статочным признаком цепной реакции. В качестве примера

можно

привести реакцию термического разложения оксида

азота

N26:

2 2

3. N

2 2

CT->N

+O,

O+O-*N

Здесь

атомы кислорода образуются в результате термически

активированной реакции распада молекулы N

O и в последую-

щих стадиях не приводят к образованию новых активных ча-

стиц.

2. Классификация элементарных стадий

зависимости от роли в развитии цепной реакции элемен-

тарные стадии классифицируют следующим образом: 1) зарож-

дение

цепей; 2) продолжение цепей; 3) разветвление цепей;

обрыв цепей.

Реакциями

зарождения цепей называют реакции превраще-

ния исходных молекул, приводящие к образованию активных

частиц, например:

реакциях продолжения цепей активные частицы взаимо-

действуют с молекулами исходных веществ с образованием но-

вых активных частиц,

причем

общее число активных частиц со-

храняется:

СН

ОН->СН

+Н

О.

реакциям продолжения относятся также процессы, в кото-

рых одна активная частица заменяется другой, но не расходу-

ется

молекула исходного вещества или (и) не образуется

лскула продукта:

R + O

->RO

-*•

+н,

СН

СЮ->СН

ООН.

Реакциями

разветвления

цепей

называют реакции, в резуль-

тате

которых увеличивается число активных частиц:

+ О

-+ОН4 О,

NC1

+ NC1

-+ N

ЗС1.

реакциям

обрыва

цепей

относятся

реакции, приводящие к

исчезновению активных частиц. В зависимости от порядка ре-

акции

по активным частицам различают линейный- и квад-

ратичный обрывы цепей:

С1

стенка

-^1/2С1

) . . *

линейный обрыв,

* Н

+ М—квадратичный обрыв.

Неразветвленные

цепные

реакции

В качестве примера неразветвленной цепной реакции рас-

смотрим реакцию водорода с хлором. Важнейшими стадиями

механизма этой реакции являются следующие:

0) C

или

—НС1

+ Н,

В механизме не учитывается первичная диссоциация водо-

рода, поскольку ее энергия

(448,9

кДж/моль) почти в два ра-

за превышает энергию диссоциации хлора

(238,9

кДж/моль).

Не

учитываются также процессы рекомбинации:

н+а+м-^на+м.

Эти процессы вследствие малой концентрации атомов водоро-

да, обусловленной их высокой активностью, не

могут

конкури-

ровать с процессами (3) и (4).

В то же время тормозящее влияние различных посторонних

примесей (О

, СЮ

, NC1

, NH

и др.) приводит к необходимо-

сти

учета

процессов обрыва цепей, связанных с гибелью актив-

ных частиц (Н, С1) при взаимодействии их с молекулами при-

месей:

н+о

+м->но

+м,

М->СЮ

+М,

за которыми

следуют

процессы

Н,

С1

НО

-*Н

НС1

+ О

Н,

С1

СЮ

-*НС1,

С1

+ О

Одно из ярких проявлений тормозящего действия примесей

выражается в существовании так называемого

периода

индук-

ции цепных реакций.

Кинетика

неразветвленных

цепных

реакций.

Кинетику

неразветвленных цепных реакций

удобно

описывать исходя из

понятия

средней

длины

цепи,

под которой понимают среднее

число актов продолжения цепи, начиная с появления актив-

ной

частицы в акте зарождения и кончая обрывом цепи.

Обозначим через а вероятность продолжения цепи,

тогда

вероятность того, что цепь

будет

состоять из s звеньев, равна

(l-cc)

(l-P)

(4.1)

где р=1—a — вероятность обрыва цепи.

Среднюю длину цепи v можно найти как математическое

ожидание случайной величины s с вероятностью Р:

Если вероятность обрыва цепей мала, то средняя длина цепи

равИа обратной вероятности обрыва цепей: v=l/f$.

Каждая цепь, начинающаяся с момента зарождения актив-

ной

частицы, приводит к образованию s молекул продукта ре-

акции,

а w

активных частиц, зарождающихся в.единицу вре-

мени,

— к образованию w$v молекул продукта. Таким образом,

скорость неразветвленной цепной реакции равна

w = w

v =

/Р

(4.3)

определяется целиком факторами, влияющими на скорость

зарождения и обрыва цепей.

Скорость неразветвленной цепной реакции можно описать

также исходя из предположения, что в

ходе

реакции наблюда-

ется только линейный обрыв цепей. В этом

случае

для ско-