Schulz M. Control Theory in Physics and Other Fields of Science: Concepts, Tools, and Applications

Подождите немного. Документ загружается.

14 1 Introduction

arguments explaining the appearance of stochastic processes on the basis of

originally deterministic equations of motion are presented.

In Chap. 7 we derive the basic equations for the open-loop and the feed-

back control of stochastic-driven systems. These equations are very similar

to the corresponding relations for deterministic control theories, although the

meaning of the involved quantities is more or less generalized. However, the

deterministic case is always a special limit of the stochastic control equations.

Another important point related to stochastic control problems are the

meaning of ﬁlters which may be used to reconstruct the real dynamics of

the system. Such techniques, as also the estimation of noise processes and the

prediction of partially unknown dynamic processes as a robust basis for an

eﬀective control, are the content of Chap. 8.

From a physical point of view a more exotic topic is the application of

game theoretical concepts to control problems. Several quantum mechanical

experiments are eventually suitable candidates for these methods. Chapter 9

explains the diﬀerence between deterministic and stochastic games as well as

several problems related to zero-sum games and the Nash equilibrium and

gives some inspirations how these methods may be applied to the control of

physical processes.

Finally, Chap. 10 presents some general concepts of optimization proce-

dures. As mentioned above, most control problems can be split into a set of

evolution equations and a remaining optimization problem. In this sense, the

last chapter of this book may be understood as a certain tool of stimulations

for solving such optimization problems.

References

1. H.G. Schuster: Deterministic Chaos: An Introduction, 2nd edn (VCH Verlags-

gesellschaft, Weinheim, 1988) 4

2. K.T. Alligood, T.D. Sauer, J.D. Farmer, R. Shaw: An Introduction to Dynamical

Systems (Springer, Berlin Heidelberg New York, 1997) 4

3. R. Balescu: Equilibrium and Nonequilibrium Statistical Mechanics (Wiley, New

York, 1975) 4

4. L. Boltzmann: J. f. Math. 100, 201 (1887) 4

5. J.W. Gibbs: Elementary Principles in Statistical Mechanics (Yale University

Press, New Haven, CT, 1902) 4

6. I. Sinai: Russian Math. Surv. 25, 137 (1970) 5

7. V.I. Arnold, A. Avez: Ergodic Problems of Classical Mechanics, Foundations

and Applications (Benjamin, New York, 1968) 6

8. A.M. Turing: Proc. London Math. Soc., Ser. 2 42, 230 (1936) 9

9. K. G¨odel: Monatshefte f¨ur Math. u. Physik 38, 173 (1931) 9

10. K.S. Scott: Oscillations, Waves and Chaos in Chemical Kinetics (Oxford Uni-

versity Press, New York, 1994) 11

11. F. Leyvraz, S. Redner: Phys. Rev. Lett. 66, 2168 (1991) 12

12. T.J. Cox, D. Griﬀeath: Ann. Prob. 14, 347 (1986) 12

References 15

13. C.R. Doering, D. Ben-Avraham: Phys. Rev. A 38, 3035 (1988) 12

14. I.M. Lifshitz: Zh. Eksp. Teor. Fiz. 42, 1354 (1962) 12

15. I.M. Lifshitz, V.V. Slyozov: J. Phys. Chem. Solids 19, 35 (1961) 12

16. C. Wagner: Z. Elektrochem. 65, 581 (1961) 12

17. S.R. Broadbent, J.M. Hammersley: Proc. Camb. Phil. Soc. 53, 629 (1957) 12

18. R.J. Baxter, A.J. Guttmann: J. Phys. A 21, 3193 (1988) 12

19. W. Kinzel: Z. Physik B 58, 229 (1985) 12

20. C. Becco: Tracking et mod´elisation de bancs de poisons. Thesis, University of

Li`ege (2004) 12

21. M. Schulz: Statistical Physics and Economics (Springer, Berlin Heidelberg New

York, 2003) 12

22. W. Paul, J. Baschnagel: Stochastic Processes: From Physics to Finance

(Springer, Berlin Heidelberg New York, 2000) 12

23. R.N. Mantegna, H.E. Stanley: Physics investigations Of ﬁnancial markets.

In: Proceedings of the International School of Physics ’Enrico Fermi’, Course

CXXXIV ed by F. Mallamace, H.E. Stanley (IOS Press, Amsterdam, 1997) 12

24. A. Bunde, Jan F. Eichner, S. Havlin, E. Koscielny-Bunde, H.-J. Schellnhuber,

D. Vjushin: Phys. Rev. Lett. 92, 039801 (2004) 12

25. B. Berkowitz, H. Scher: Phys. Rev. Lett. 79, 4038 (1997) 12

26. D. Sornette, L. Knopoﬀ, Y.Y. Kagan, C. Vanneste: J. Geophys. Res. 101, 13883

(1996) 12

27. J.R. Grasso, D. Sornette: J. Geophys. Res. 103, 29965 (1998) 12

Deterministic Control Theory

2.1 Introduction: The Brachistochrone Problem

In this chapter we focus our attention on the open loop control of deterministic

problems. We will see that the language of deterministic control theory is

close to the language of classical mechanics. The deterministic control theory

requires that the dynamics of the system under control is completely deﬁned

by well-deﬁned equations of motion and accurate initial conditions. Although

the theoretical description is not inﬂuenced by the degree of complexity of the

system, the subsequently presented methods are useful if the system has only

a few degrees of freedom. The causes of this unpleasant restriction for the

practical application of the techniques presented was discussed in Sect. 1.2.

As a very simple introduction, we consider a particle which moves in a two-

dimensional space along a ﬁxed curve in a potential V (x, y) without friction.

A typical control problem is now the question that what form should the

curve have so that for a given initial kinetic energy the particle moves from

a given point to another well-deﬁned point in the shortest time? This is the

brachistochrone problem formulated originally by Galilei [1] and solved by

Bernoulli [2]. In principle, the brachistochrone problem can be formulated on

the basis of several concepts. The ﬁrst way is to interpret the control of the

system by the choice of the boundary condition which ﬁxes the particle at

the curve. Let y(x) be the form of the curve (Fig. 2.1). The position of the

particle is given by the coordinates x =(x, y) so that the initial position may

be deﬁned by x

=(x

) with y

= y(x

) while the ﬁnal position is given

by x

=(x

) with y

= y(x

). Furthermore, the conservative force ﬁeld

requires a potential V (x) and we obtain the conservation of the total energy

+ V (x)=E, (2.1)

where v is the velocity of the particle. Thus, the time dt required for the

passage of the curve segment ds =



+dy

is simply

M. Schulz: Control Theory in Physics and other Fields of Science

STMP 215, 17–60 (2006)

 Springer-Verlag Berlin Heidelberg 2006

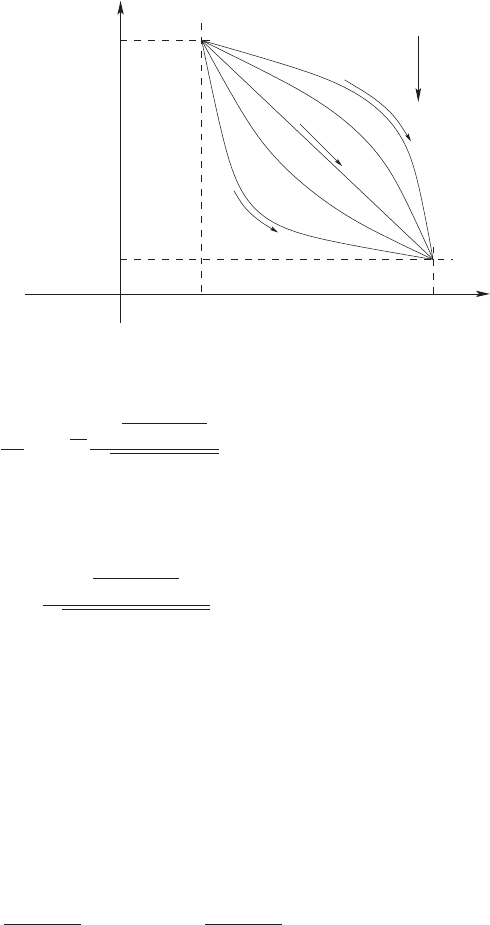
18 2 Deterministic Control Theory

Fig. 2.1. The original brachistochrone problem solved by Bernoulli: which path in

a homogeneous gravity ﬁeld between (x

)and(x

) is the fastest trajectory?

dt =

|v|

√



1+y

2

(x)



2(E − V (x))

dx, (2.2)

and the above-introduced optimum curve minimizing the duration time T

between the initial point and the ﬁnal point follows from the solution of the

minimum problem

T =





1+y

2

(x)



2(E − V (x, y(x))

→ inf , (2.3)

considering the initial and ﬁnal conditions y

= y(x

)andy

= y(x

), respec-

tively. The solution of (2.3) belongs to a classical variational problem [2, 3].

The brachistochrone problem can be also formulated as a optimum con-

trol by external forces. To this aim we write the curve in a parametric form

(x(t),y(t)). The curve y = y(x) may be expressed by the implicit relation

U(x(t),y(t)) = 0. Thus, the motion of the particle along the curve requires

immediately

˙x + u

˙y = 0 (2.4)

with

∂U (x, y)

∂x

and u

∂U (x, y)

∂y

. (2.5)

On the other hand, when the particle moves along the curve, two forces act on

the particle. The ﬁrst force, F = −∇V , is due to the potential V , the second

force is the reaction of support, u =(u

), which is perpendicular to the

velocity. Without the knowledge of condition (2.4), the second force cannot be

2.2 The Deterministic Control Problem 19

distinguished by physical arguments from an additional external force acting

on the free particle in the potential V . Thus, we get the equations of motion

¨x = −

∂V

∂x

+ u

and ¨y = −

∂V

∂y

+ u

, (2.6)

and the optimum control problem is now reduced to the minimum problem

T → inf with x(0) = x

and x(T )=x

(2.7)

with the equations of motion (2.6) and condition (2.4) shrinking the external

forces u =(u

) on such forces which are equivalent to the reaction of

support. As we will see later, representation (2.6) is a characteristic of the

optimal control problem via external force ﬁelds.

2.2 The Deterministic Control Problem

2.2.1 Functionals, Constraints, and Boundary Conditions

Let us start with a preliminary formulation of an optimal control problem.

To this aim, we consider a dynamical system over a certain horizon T ,which

means we have a problem wherein the time t belongs to an interval [0,T] with

T<∞. As discussed in the introduction, each control problem is deﬁned

by two groups of variables. The ﬁrst group are the state variables X with

X = {X

,...,X

}. The set of all allowed vectors X spans the phase space

P (or the reduced phase space P

rel

) of the underlying system. The physically

motivated strict distinction between the phase space P, which contains all

degrees of freedom, and the reduced phase space P

rel

, which contains only the

relevant degrees of freedom, is no longer necessary for the moment. Hence,

we use simply the notation ‘phase space’ for both, P and P

rel

. The second

group belongs to the input or control variables u = {u

,...,u

}.Thesetof

all allowed control variables form the control space U.

After this fundamental deﬁnitions, we may deﬁne the mathematical com-

ponents of a deterministic control problem. In principle, this problem requires

the consideration of constraints, boundary conditions, and functionals.

Boundary conditions are imposed on the end points of the time interval

[0,T] considered in the current control problem. These conditions belong only

to the trajectory X(t) of the system. Characteristic boundary conditions are

• boundary conditions with ﬁxed end points, i.e., X(0) = X

and X(T )=X

• periodic boundary conditions, where the trajectory X(t) has the same val-

ues on both end points, i.e., X(0) = X(T ), and

• boundary conditions with one ore two free ends.

Functionals deﬁne the control aim. These functionals are often denoted

as performance or cost functional which should be minimized to obtain the

20 2 Deterministic Control Theory

optimum control u

∗

(t) and a corresponding optimum trajectory X

∗

(t). There

are three standard types of functionals. Integral functionals have the form

R[X, u, T]=



dtφ(t, X(t),

X(t),u(t)) , (2.8)

where the integrand L : R × P × P × U → R is called the performance func-

tion or the Lagrangian. We will demonstrate in the subsequent section that

this Lagrangian is equivalent under certain conditions to the Lagrangian of

classical mechanics. The second type of functionals representing a performance

are endpoint functionals. These functionals depend on the terminal values of

the trajectory

S[X, u, T ]=Φ(X(0),X(T),T) . (2.9)

Finally, we may consider mixed functionals, deﬁned by a linear combinations

of (2.8) and (2.9).

Constraints are either functional equalities, G

[t, X(t),u(t)] = 0, or func-

tional inequalities G

[t, X(t),u(t)] ≤ 0, where α =1, 2,... is the number of

constraints. Constraints of the form

X(t)=F (X, u, t) (2.10)

are called diﬀerential constraints. These constraints often correspond to the

evolution equations, e.g., the deterministic part of (1.4) or the canonical sys-

tem (1.1). Constraints which do not depend on the derivatives and controls

are called geometrical constraints, e.g., g

[t, X(t)] = 0 or g

[t, X(t)] ≤ 0. In

general, we may conclude that constraints ﬁx at least partially the trajectory

of the system through the phase space.

2.2.2 Weak and Strong Minima

The solution of a control problem is equivalent to the determination of the

minimum of the corresponding performance functional

R[X, u, T] → inf (2.11)

considering the constraints and the boundary conditions. The solution of this

problem is an optimum control u

∗

(t) and an optimum trajectory X

∗

(t). We

denote (2.11) together with the corresponding constraints and the boundary

conditions as a Lagrange problem if R[X, u, T ] is an integral. If R[X, u, T]is

an endpoint functional, the problem is called the Meier problem and we speak

about a Bolza problem in the case of a mixed functional. However, it is simple

to demonstrate that this historically motivated distinction is not necessary,

because all three apparently diﬀerent problems are essentially equivalent. For

example, the integral representation (2.8) can be transformed into an endpoint

functional by introducing a new degree of freedom X

N+1

with a new equation

of motion

2.2 The Deterministic Control Problem 21

N+1

(t)=φ(t, X(t),

X(t),u(t)) (2.12)

as an additional constraint and the additional boundary condition X

N+1

(0) =

0. Then, the Lagrange problem (2.8) can be written as a Meier problem

R[X, u, T]=



N+1

(t)=X

N+1

(T ) → inf (2.13)

now with R[X, u,T ] as an endpoint functional.

Let us assume that the pair {X(t),u(t)} satisﬁes both the constraints

and the boundary conditions. Generally, there exists a noncountable set of

such pairs. This may be illustrated by a simple example. We may choose an

arbitrary function u(t) and solve the evolution equation (2.10) and the given

boundary conditions. Obviously, we will always succeed with this procedure,

at least for a suﬃciently large class of functions u(t). In the future we deﬁne

that such a pair {X(t),u(t)} is said to be admissible for the control problem.

An admissible pair {X

∗

(t),u

∗

(t)} yields a local weak minimum (or a weak

solution) of the control problem if the inequality

R[X, u, T] ≥ R[X

∗

,T] (2.14)

holds for any admissible pairs {X(t),u(t)} which satisfy the inequalities

X −X

∗

≤ε 

X −

∗

≤ε and u − u

∗

≤ε, (2.15)

where we use the maximum norm

ξ = max

t∈[0,T ]

|ξ(t)| (2.16)

for any suﬃciently small ε. In what follows we call the small diﬀerences

δX(t)=X(t)−X

∗

(t)andδu(t)=u(t)−u

∗

(t), respectively, variations around

the (weak) minimum {X

∗

(t),u

∗

(t)}. A weak minimum is not necessarily stable

against arbitrary velocity variations δ

X(t) or strong variations of the control

function δu(t). We speak about a strong minimum if inequality (2.14) holds

for all admissible pairs {X(t),u(t)} satisfying the inequality

X −X

∗

≤ε. (2.17)

In other words, a strong minimum is not aﬀected by arbitrary ﬂuctuations of

the velocity

X(t) and the control function u(t). That means especially that

there is no better control function u(t) than u

∗

(t) for all trajectories close to

∗

(t). Each strong minimum is always a weak minimum, but a weak minimum

is not necessarily a strong minimum. Finally, if inequality (2.14) holds for all

admissible pairs {X(t),u(t)} , the pair {X

∗

(t),u

∗

(t)} is called the optimum

solution of the control problem.

The general problem of optimum control theory can now be reformulated.

In a ﬁrst step we have to ﬁnd all extremal solutions of the functional R[X, u, T ]

considering the constraints and the boundary conditions, and then, we have to

check whether these extrema are the optimum solution of the control problem.

22 2 Deterministic Control Theory

2.3 The Simplest Control Problem: Classical Mechanics

2.3.1 Euler–Lagrange Equations

The simplest control problem contains no control function and no constraints.

Thus (2.8) reduces to the special functional

S[X, T]=



dtL(t, X(t),

X(t)) (2.18)

with ﬁxed points X(0) = X

and X(T )=X

as boundary conditions. From

a physical point of view, functional (2.18) can be identiﬁed as the well-known

mechanical action. Here, the function L is the Lagrangian L = E

kin

− U, de-

ﬁned as the diﬀerence between the kinetic energy E

kin



/2 and the

potential U = U (X) of a conservative mechanical system. Each N-dimensional

vector X ∈ P denotes the position of system in the phase space. It should be

denoted that in the framework of the present problem the phase space P does

not correspond to the standard deﬁnition of classical mechanics. Because P

contains only the coordinates of the system and not the momenta, this space

is sometimes called the conﬁguration space. The fact that the function L only

contains X(t)and

X(t) but no higher derivatives

X(t), ...means that a me-

chanical state is completely deﬁned by the coordinates and the velocities. The

Hamilton principle (the principle of least action) requires that the trajectory

of the system through the phase space corresponds to the optimum trajectory

∗

(t) of the problem S[X, T] → inf. The solution of this optimum problem

leads to the equations of motion of the underlying system which are also

denoted as Euler–Lagrange equations.

For the moment we should generalize the physical problem to an arbitrary

Lagrangian. The only necessary condition is that the Lagrangian must be

continuously diﬀerentiable. From this very general point of view, the Euler–

Lagrange equations are the necessary conditions that a certain admissible

trajectory corresponds to an extremum of the action S[X, T ].

Let us now derive the Euler–Lagrange equations in a mathematically rig-

orous way. That is necessary in order to understand several stability problems

which may become important for the subsequent discussion of the general

optimal control problem. The solution of this extremum problem consists of

three stages.

The initial step is the calculation of the ﬁrst-order variation. To this aim

we assume that X

∗

(t) is a trajectory corresponding to an extremum of S[X, T]

with respect to the boundary conditions. The addition of an arbitrary inﬁnites-

imal small variation δX(t) with the boundary conditions δX(0) = δX(T )=0

generates a new trajectory X(t)=X

∗

(t)+δX(t) in the neighborhood of the

optimum trajectory. We conclude that all trajectories X(t) are again admis-

sible functions due to the special choice of the boundary conditions for the

variation δX(t). Thus, we obtain

2.3 The Simplest Control Problem: Classical Mechanics 23

δS[X

∗

,T]=S[X

∗

+ δX,T] − S[X

∗

,T]



dtL(t, X

∗

(t)+δX(t),

∗

(t)+δ

X(t))

−



dtL(t, X

∗

(t),

∗

(t))





f(t)δX(t)+p(t)δ

X(t)



(2.19)

with the force

f(t)=

∂L

∂X

∗

(t, X

∗

) (2.20)

and the momentum

p(t)=

∂L

∂

∗

(t, X

∗

) . (2.21)

The second step is the integration by parts. There are two possibilities. Fol-

lowing Lagrange, we have to integrate by parts the second term of (2.19)

while following DuBois–Reymond, we integrate by parts the ﬁrst term. The

way of Lagrange assumes a further assumption about the smoothness of the

Lagrangian, namely that the generalized momentum (2.21) is continuous dif-

ferentiable with respect to time. Under this additional condition we obtain

δS[X

∗

,T]=



dt [f(t) − ˙p(t)] δX(t) . (2.22)

The integration by parts according to DuBois–Reymond yields

δS[X

∗

,T]=







p(t) −



f(τ)dτ





X(t) . (2.23)

Both representations, (2.22) and (2.23), are essentially equivalent.

The assumption that X

∗

(t) corresponds to an extremum of S[X, T ]au-

tomatically requires δS[X

∗

,T] = 0. Thus, the last stage consists in solving

(2.22) and (2.23) considering δS[X

∗

,T] = 0. The mathematical proof of this

statement is the most diﬃcult part of the derivation. For the sake of simplic-

ity, we restrict our conclusions on some intuitive arguments. It is obvious that

in the case of (2.22) the condition δS[X

∗

,T] = 0 for all possible variations

δX(t) automatically requires ˙p(t)=f (t) or with (2.20) and (2.21)

Both, force and momentum, are N -dimensional vectors with the components

(t)=∂L/∂X

∗

and p

(t)=∂L/∂

∗

24 2 Deterministic Control Theory



∂L

∂

∗

(t, X

∗

)



∂L

∂X

∗

(t, X

∗

) . (2.24)

This is the Euler–Lagrange equation in the Lagrange representation. The sec-

ond way, originally given by DuBois–Reymond, leads to

p(t)=



f(τ)dτ + c

, (2.25)

where c

is an arbitrary constant. In other words, if the expression in the brack-

ets of (2.23) has a constant value, the integral vanishes due to the boundary

conditions for δX(t). Because δS[X

∗

,T] = 0 should be valid for all admissible

variations, the only solution is (2.25). The explicit form of (2.25) reads

∂L

∂

∗

(t, X

∗



∂L

∂X

∗

(τ,X

∗

(τ),

∗

(τ))dτ + c

. (2.26)

This equation is also called the DuBois–Reymond representation of the Euler–

Lagrange equation. For details of the proof we refer to the literature [5, 6, 7,

8, 9, 10, 11, 12].

Physically both (2.24) and (2.26) are equivalent representations of the

same problem. Mathematically, (2.26) has the advantage that we need no fur-

ther assumption about the existence of second-order derivatives of the La-

grangian. But apart from these subtleties, (2.24) and (2.26), respectively,

represent the solution of the extremal problem. The solution of the Euler–

Lagrange equation, X

∗

(t) is also called an extremal. In classical mechanics,

(2.24) is completely equivalent to the Newtonian equations of motion. The

only diﬀerence belongs to the boundary conditions. A typical problem of New-

tonian mechanics is usually related to diﬀerential equations with initial con-

ditions, X(0) = X

and

X(0) =

, while the above-derived Euler–Lagrange

equations have boundary conditions at both ends of the time interval [0,T].

2.3.2 Optimum Criterion

Weierstrass Criterion

The Euler–Lagrange equations are only a necessary condition for an extremum

of the action S[X, T]. For the solution of the optimum problem we need an

additional criterion which allows us to decide whether an extremal solution

∗

(t) corresponds to a local minimum or not. The Weierstrass criterion em-

ploys the same smoothness requirement used for the derivation of the Euler

Lagrange equations, namely that the Lagrangian is continuously diﬀerentiable.

The derivation of this criterion is simple and very instructive for our further

procedure. To this aim we introduce a special variation (see also Fig. 2.2).

It can be shown that this diﬀerence is only an apparent contradiction. Each of

the two boundary conditions can be transformed into the other.