Schulz M. Control Theory in Physics and Other Fields of Science: Concepts, Tools, and Applications
Подождите немного. Документ загружается.

166 6 Nonequilibrium Statistical Physics
Suppose we know all sets B
i
which could condition the appearance of an event
in the set A.TheB
i
should be mutually exclusive, B
i
∩B
j
= Ø for all i = j,
and exhaustive,
6
i
B
i
= Ω. Thus we obtain
P (A)=P (A ∩ Ω)=P
A ∩
3
i
B
i
= P
3
i
(A ∩ B
i
)
. (6.63)
If we take into account (A ∩ B
i
) ∩ (A ∩ B
j
) = Ø we obtain due to (6.2)and
(6.61)
P (A)=
i
P (A ∩ B
i
)=
i
P (A | B
i
) P (B
i
) . (6.64)
This general relation specifies in the case of the probability density immedi-
ately to
p(X, t)=
p (X, t | X
0
,t
0
) p (X
0
,t
0
)dX
0
. (6.65)
Because of the symmetry P (A ∩ B)=P (B ∩A) we also get
p(X
0
,t
0
)=
p (X, t | X
0
,t
0
) p (X
0
,t
0
)dX. (6.66)
Due to (6.60), the last equation is a simple identity. Equation (6.62) permits
in particular the extension of the initial condition (6.26) on any probability
distributions.
This constitutes a warning that it is always preferable to represent each
joint probability distribution function p (X, t; Z, τ) in the form (6.62). If we
want to generally determine this joint probability for t>τ>t
0
, then we
must calculate the integral
p (X, t; Z, τ)=
dX
0
p (X, t | Z, τ; X
0
,t
0
)
× p (Z, τ | X
0
,t
0
) p (X
0
,t
0
) (6.67)
in which the conditional probability p (X, t | Z, τ; X
0
,t
0
) occurs. The reason
for the more complicated structure consists in the fact that the determinis-
tic character of the microscopic dynamics is possibly partially conserved on
the level of the relevant degrees of freedom. Hence, a certain memory of the
initial information remains, which is, for instance, expressed by the appear-
ance of the memory kernel
ˆ
K(t −t
) in the Nakajima–Zwanzig equation. This
effect indicates a possible feedback between the relevant degrees of freedom
via the hidden irrelevant degrees of freedom. Only if this feedback disap-
pears, p (X, t | Z, τ; X
0
,t
0
)=p (X, t | Z, τ) applies and the simpler relation-
ship p (X, t; Z, τ)=p (X, t | Z, τ) ρ (Z, τ) becomes valid for arbitrary points
in time (Fig. 6.2). On the other hand, (6.62) is always valid. The correctness
of this relation is justified by the fact that relevant and irrelevant degrees of
freedom are assumed to be initially uncorrelated even if former information is
unknown. We point out again that this assumption has to be understood in
the sense of the Bayesian definition of statistics.

6.6 Markov Approximation 167
(Z,τ)
(Y,t)
(Y
0
,t
0
)
Fig. 6.2. Possible contributions to the joint probability density p(Y,t; Z, τ; Y
0
,t
0
).
The integration over all positions Y
0
leads to p(Y,t; Z, τ). Only the full trajecto-
ries contribute to the conditional probability density p(Z, τ | Y
0
,t
0
)aswellasto
the conditional probability density p(Y, t | Z, τ; Y
0
,t
0
). These events form together
with the probability density p(Y
0
,t
0
) the joint probability p(Y,t; Z, τ; Y
0
,t
0
). The
dashed curves are also contained in p(Z, τ | Y
0
,t
0
) but not in p(Y,t; Z, τ ). Roughly
speaking, they are filtered out due to conditional probability p(Y,t; | Z, τ; Y
0
,t
0
)in
the expression p(Y,t; Z, τ; Y
0
,t
0
)=p(Y,t; | Z, τ ; Y
0
,t
0
)p(Z, τ | Y
0
,t
0
)p(Y
0
,t
0
). On
the other hand, the product p(Y,t; | Z, τ)p(Z, τ | Y
0
,t
0
)p(Y
0
,t
0
) also considers the
dotted lines which contribute particularly to p(Y,t | Z, τ ).Thus,wehavetoexpect
p(Y,t; | Z, τ; Y
0
,t
0
) = p(Y,t; | Z, τ). The equivalence between both quantities holds
only if no memory effect appears
6.6 Markov Approximation
We once again return to the problem of the selection of relevant degrees of
freedom. If we define the relevant degrees of the complex system in such a
way that all these variables change relatively slow compared to the irrelevant
degrees of freedom, then the memory kernel (6.41) of the Nakajima–Zwanzig
equation may approach
ˆ
K (t
0
,t− t
)=
ˆ
K (t
0
) δ (t − t
) . (6.68)
This representation is called the Markov approximation [4, 12]. The assump-
tion of such a separation between slow, relevant time scales and fast, irrele-
vant time scales is at least an appropriate approximation for many complex
systems. But it should be remarked that there is really no such thing as a
system with the Markov character. If we observe the system on a very fine
time scale, the immediate history will almost certainly be required to predict
the probabilistic development. In other words, there is a certain characteristic
time during which the previous history is important. However, systems whose
memory time is so small may be, on the time scale on which we carry out
observations, assumed to be a Markov-like system. We substitute (6.68)in
the Nakajima–Zwanzig equation (6.39)toget
∂p(X, t | X
0
,t
0
)
∂t
= −
ˆ
L
markov
p (X, t | X
0
,t
0
) (6.69)
168 6 Nonequilibrium Statistical Physics
with the Markovian
ˆ
L
markov
=
ˆ
M (t
0
) −
ˆ
K(t
0
). However, we also know about
situations where a part of the irrelevant degrees of freedom is considerably
slower than the relevant degrees of freedom and only the remaining part of
the irrelevant degrees of freedom contributes to the fast dynamics. In these
cases, it seems to be more favorable to derive the evolution equation for the
probability density p (X, t | X
0
,t
0
) by the use of time-dependent projectors
capturing the effects of the slow irrelevant dynamics.
Such generalization basically changes nothing of the general procedure of
the separation of the time scales, except for the occurrence of an explicit time
dependence of the operator
ˆ
L
markov
(t). Therefore, we can also use the Markov
approximation for these problems. However, the concept of the separation of
time scales fails or becomes uncontrolled if a suitable set of irrelevant degrees
of freedom offers characteristic time scales similar to those of the relevant
degrees of freedom. By assuming an infinitesimal time interval dt we obtain
from (6.69)
p (X, t +dt | X
0
,t
0
)=
1 −
ˆ
L
markov
(t)dt
p (X, t | X
0
,t
0
) . (6.70)
In general, we may express the operator 1 −
ˆ
L
markov
(t)dt by an integral rep-
resentation using the transition function U
markov
(X, t + dt | Z, t)
p (X, t +dt | X
0
,t
0
)=
dZU
markov
(X, t +dt | Z, t) p (Z, t | X
0
,t
0
) . (6.71)
We multiply (6.71) with the initial distribution function p (X
0
,t
0
) and inte-
grate over all configurations X
0
. Considering (6.65)weget
p (X, t +dt)=
dZU
markov
(X, t +dt | Z, t) p (Z, t) . (6.72)
Thus, the integral kernel U
markov
(X, t +dt | Z, t) can interpreted as the con-
ditional probability density p (X, t +dt | Z, t) for a transition from the state Z
at time t to the state X at time t+dt. This necessitates a further explanation.
We remember that (6.67) requires the more general relation
p (X, t +dt)=
dX
0
dZp(X, t +dt | Z, t; X
0
,t
0
)
× p (Z, t | X
0
,t
0
) p (X
0
,t
0
) . (6.73)
A simple comparison between (6.72) and (6.73) leads to the necessary con-
dition p (X, t +dt | Z, t; X
0
,t
0
)=p (X, t +dt | Z, t). This is simply another
formulation of the Markov property. It is, even by itself, extremely powerful.
In particular, this property means that we can define higher conditional and
joint probabilities in terms of the simple conditional probability. To obtain a
general relation between the conditional probabilities at different times, we
shift the time t → t +dt in (6.71) and obtain
p (X, t +2dt | Y
0
,t
0
)=
dY p(X, t +2dt | Y,t + dt)
× p (Y, t + dt | X
0
,t
0
) . (6.74)

6.7 Generalized Fokker–Planck Equation 169
On the other hand, the transformation dt → 2dt leads to
p (X, t +2dt | Y
0
,t
0
)=
dZ p (X, t +2dt | Z, t) p (Z, t | Y
0
,t
0
) . (6.75)
so that we obtain from (6.71), (6.74), and (6.75)
p (X, t +2dt | Z, t)=
dYp(X, t +2dt | Y,t +dt)
× p (Y, t +dt | Z, t) . (6.76)
When repeating this procedure infinite times, one obtains a relation for finite
time differences
p (X, t | Z, t
)=
dYp(X, t | Y,t
) p (Y,t
| Z, t
) , (6.77)
which is the Chapman–Kolmogorov equation. This equation is a rather com-
plex nonlinear functional equation relating all conditional probabilities ob-
tained from a given Markovian to each other.
This is a remarkable result: the conditional probability density obtained
from an arbitrary Markovian must satisfy the Chapman–Kolmogorov equa-
tion. In addition, the Chapman–Kolmogorov equation is an important crite-
rion for the presence of the Markov property. Whenever empirically deter-
mined conditional probabilities satisfy (6.77) we are able to introduce the
Markov property.
6.7 Generalized Fokker–Planck Equation
6.7.1 Differential Chapman–Kolmogorov Equation
The determination of the Markovian for a given process on the basis of a
microscopic theory is probably excluded. Therefore, we are always dependent
on empirical considerations and observations. It would be reasonable if we
would know some rules from which the Markovian
ˆ
L
markov
can be constructed.
For all evolution processes with Markov properties the parameter-free
Chapman–Kolmogorov equation (6.77) is a universal relation. However, the
Chapman–Kolmogorov equation has many solutions. In particular, for a given
dimension N of the state X, every solution of (6.69) must also be a solution
of (6.77), independent of the special mathematical structure of the operator
ˆ
L
markov
. Therefore, we can possibly use this equation to obtain information
about the general mathematical structure of
ˆ
L
markov
. To do so we follow Gar-
diner [11] and define the subsequent quantities for all ε>0:
F
α
(Z, t) = lim
δt→0
1
δt
|Y −Z|<ε
dYp(Y,t + δt | Z, t) ∆Y
α
+ o(ε) , (6.78)
and
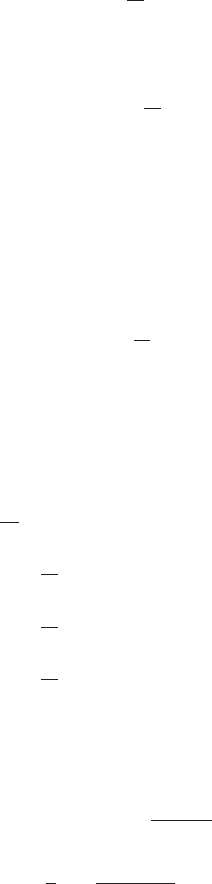
170 6 Nonequilibrium Statistical Physics
D
αβ
(Z, t) = lim
δt→0
1
δt
|Y −Z| <ε
dYp(Y,t + δt | Z, t) ∆Y
α
∆Y
β
+ o(ε) , (6.79)
where we have used the notation ∆Y
α
= Y
α
− Z
α
. Furthermore we introduce
W (Y | Z; t) = lim
δt→0
1
δt
p (Y,t + δt | Z, t) (6.80)
for |Y − Z| >ε. We will see later that these quantities were chosen in a very
natural way. They can be obtained directly from observations or they are
defined by suitable model assumptions.
If we are able to build the Markovian
ˆ
L
markov
by the exclusive use of
these quantities, we have reached our goal. Note that possible higher-order
coefficients must vanish for ε → 0. For instance, the third-order quantity
defined by
C
αβγ
(Z, t) = lim
δt→0
1
δt
|Y −Z|<ε
dYp(Y,t + δt | Z, t) ∆Y
α
∆Y
β
∆Y
γ
(6.81)
may be approximated by |C
αβγ
||D
αβ
|ε = o (ε). Thus, if D
αβ
exists, the
coefficient C
αβγ
is of an order of magnitude o (ε) and disappears for ε → 0. To
proceed, we consider the time evolution of the average of an arbitrary function
f which is twice continuously differentiable
∂
∂t
dZf (Z) p (Z, t | Y,t
)
= lim
δt→0
1
δt
dZf (Z)[p (Z, t + δt | Y, t
) − p (Z, t | Y,t
)] dZ
= lim
δt→0
1
δt
dZdXf (Z) p (Z, t + δt | X, t) P (X, t | Y,t
)
− lim
δt→0
1
δt
dZdXf (X) p (Z, t + δt | X, t) P (X, t | Y, t
) , (6.82)
where we have used the Chapman–Kolmogorov equation (6.77) in the first
term and the normalization condition (6.60) to produce the corresponding
terms in (6.82). Since f (Z) is twice continuously differentiable, we may write
f (Z)=f (X)+
α
∂f (X)
∂X
α
[Z
α
− X
α
]
+
1
2
αβ
∂
2
f (X)
∂X
α
∂X
β
[Z
α
− X
α
][Z
β
− X
β
]+R(Z, X) , (6.83)
where the reminder function R(Z, X) vanishes for |X − Z| = ε → 0aso(ε
2
).
We now divide the integrals in (6.82) into two regions |X −Z|≤ε and
|X −Z| >εand substitute (6.83)into(6.82):
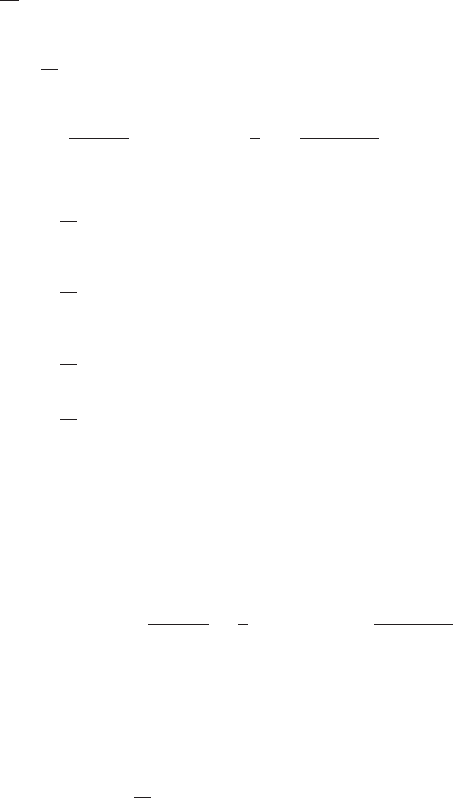
6.7 Generalized Fokker–Planck Equation 171
∂
∂t
dZf (Z) p (Z, t | Y,t
)
= lim
δt→0
1
δt
|Z−X|<ε
dZdXp(Z, t + δt | X, t) p (X, t | Y, t
)
×
α
∂f (X)
∂X
α
[Z
α
− X
α
]+
1
2
αβ
∂
2
f (X)
∂X
α
∂X
β
[Z
α
− X
α
][Z
β
− X
β
]
+ lim
δt→0
1
δt
|Z−X|<ε
dZdXR(Z, X) p (Z, t + δt | X, t) p (X, t | Y, t
)
+ lim
δt→0
1
δt
|Z−X|<ε
dZdXf (X) p (Z, t + δt | X, t) p (X, t | Y,t
)
+ lim
δt→0
1
δt
|Z−X|≥ε
dZdXf (Z) p (Z, t + δt | X, t) p (X, t | Y, t
)
− lim
δt→0
1
δt
dZdXf (X) p (Z, t + δt | X, t) p (X, t | Y,t
) . (6.84)
Let us now compute the limit ε → 0 line by line. The first term of this
expression can be transformed in the following way. We take the limit δt → 0
inside the integral to obtain with the help of (6.78) and (6.79)
(1) =
dXp(X, t | Y, t
)
×
α
F
α
(X, t)
∂f (X)
∂X
α
+
1
2
αβ
D
αβ
(X, t)
∂
2
f (X)
∂X
α
∂X
β
. (6.85)
The second term of (6.84) disappears for ε → 0 due to R(Z, X) ∼ o(|Z −X|
2
).
The third term and the fifth term can be collected in one expression. Thus,
we get
(3) + (5) = − lim
δt→0
1
δt
|Y −Z|≥ε
dZdXf (X) p (Z, t + δt | X, t)
×p (X, t | Y,t
) , (6.86)
or with the use of (6.80) and considering ε → 0
(3) + (5) = −H
dZdXf (X) W (Z | X; t) p (X, t | Y, t
) . (6.87)
Notice that we use the symbol H to indicate the principal value integral. We
finally get for the fourth term
(4) = H
dXdZf (Z) W (Z | X; t) p (X, t | Y, t
) . (6.88)
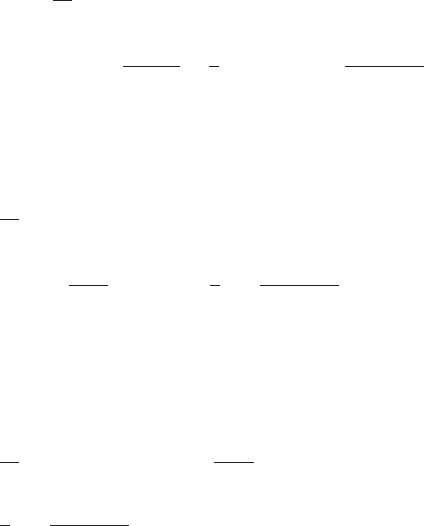
172 6 Nonequilibrium Statistical Physics
We put these all results together to obtain
dX
∂
∂t
p (X, t | Y,t
) f (X)=
dXp(X, t | Y, t
)
×
α
F
α
(X, t)
∂f(X)
∂X
α
+
1
2
αβ
D
αβ
(X, t)
∂
2
f(X)
∂X
α
∂X
β
+ H
dZdX [f (X) − f (Z)] W (X | Z; t) p (Z, t | Y, t
) (6.89)
and after integrating by parts we get
∂
∂t
dXf (X) p (X, t | Y,t
)=
dXf(X)
×
−
α
∂
∂X
α
F
α
(X, t)+
1
2
αβ
∂
2
∂X
α
∂X
β
D
αβ
(X, t)
p (X, t | Y,t
)
+ H
dZ dX [f (X) − f (Z)] W (X | Z; t) p (Z, t | Y, t
) . (6.90)
Finally we consider that we have chosen the function f to be arbitrary. We
can then deduce that the conditional probability fulfils the relation
∂
∂t
p (X, t | Y,t
)=−
α
∂
∂X
α
F
α
(X, t)p (X, t | Y,t
)
+
1
2
αβ
∂
2
∂X
α
∂X
β
D
αβ
(X, t)p (X, t | Y,t
)
+ H
dZ [W (X | Z; t) p (Z, t | Y,t
)−W (Z | X; t) p (X, t | Y,t
)] . (6.91)
This equation is the differential form of the Chapman–Kolmogorov equation
which is also denoted in the literature as the forward differential Chapman–
Kolmogorov equation. The right-hand side of this equation defines the general
structure of the Markovian
ˆ
L
markov
.
If we want to specify the differential Chapman–Kolmogorov equation we
must consider that by definition the components D
αβ
(X, t)mustformapos-
itive definite matrix and that W (X | Z; t) must be a nonnegative function.
Then it can be shown under certain conditions that a nonnegative solution
to the differential Chapman–Kolmogorov equation exists and that this solu-
tion also satisfies the Chapman–Kolmogorov equation. The conditions to be
satisfied are the initial condition
p (X, t | Y,t)=δ(X −Y ) , (6.92)
which follows directly from (6.65), and any appropriate boundary conditions.
We may also derive the backward differential Chapman–Kolmogorov equa-
tions which give the time evolution with respect to the initial variables of
p (X, t | Y,t
). To this aim we consider

6.7 Generalized Fokker–Planck Equation 173
∂
∂t
p (X, t | Y,t
) = lim
δt→0
1
δt
[p (X, t | Y,t
) − p (X, t | Y,t
− δt
)]
= lim
δt→0
1
δt
dZp(Z, t
| Y,t
− δt
) p (X, t | Y, t
)
− lim
δt→0
1
δt
dZp(X, t | Z, t
) p (Z, t
| Y,t
− δt
) (6.93)
by use of the normalization condition (6.60) in the first term and the
Chapman–Kolmogorov equation (6.77) in the second term. It is easy to
show that we can carry out the infinitesimal shift p (Z, t
| Y,t
− δt
) →
p (Z, t
+ δt
| Y,t
) without a noticeable change of (6.93). Hence we get
∂
∂t
p (X, t | Y,t
) = lim
δt→0
dZ
p (Z, t
+ δt
| Y,t
)
δt
× [p (X, t | Y,t
) − p (X, t | Z, t
)] (6.94)
and, therefore, using similar techniques to those used for the derivation of
(6.91)
∂
∂t
p (X, t | Y,t
)=−
α
F
α
(Y,t
)
∂
∂Y
α
p (X, t | Y,t
)
−
1
2
αβ
D
αβ
(Y,t
)
∂
2
∂Y
α
∂Y
β
p (X, t | Y,t
)
+ H
dZW (Z | Y ; t
)[p (X, t | Y,t
) − p (X, t | Z, t
)] . (6.95)
This equation is called the backward differential Chapman–Kolmogorov equa-
tion. We remark that the forward and the backward equations are equivalent
to each other. The main difference is which set of variables is held fixed. For
the forward equation, solutions exist for t ≥ t
and (6.92) is the initial con-
dition with respect to the free variables (X, t). In the case of the backward
equation, we hold (X, t) fixed so that since the backward equation expresses
development in t
≤ t,(6.92) is the final condition of (6.95).
6.7.2 Deterministic Processes
As we have stressed several times in the previous chapters, there are also
phenomena in complex systems, which may be described by a completely
deterministic motion. If the corresponding processes also possess a Markov
character, then they can be described by a differential Chapman–Kolmogorov
equation with B
αβ
=0andW (Y | Z; t) = 0. It remains the equation
∂
∂t
P (X, t | Y,t
)=−
α
∂
∂X
α
F
α
(X, t)P (X, t | Y,t
) . (6.96)
The solution to this equation with the initial condition (6.92)is

174 6 Nonequilibrium Statistical Physics
P (X, t | Z, t
)=δ
X −
X(t)
. (6.97)
That means the system moves along a certain trajectory
X(t) without any
uncertainty. The curve
X(t) is a solution of the ordinary differential equations
d
X
α
(t)
dt
= F
α
(
X(t),t) (6.98)
with the initial conditions
X(t
)=Y. (6.99)
Equation (6.98) are also denoted as kinetic equations. These differential equa-
tions are however generally no equations of motion in the sense of the classical
mechanics. In particular the kinetic equations are always irreversible
3
, i.e.,
they are not invariant under reversal of the time direction.
On the other hand, these equations represent the repeatedly used assump-
tion of the decoupling of relevant and irrelevant degrees of freedom. With the
knowledge of the above-discussed projection formalism we are able to refine
this statement. Decoupling means that the influence of the irrelevant degrees
of freedom to the relevant degrees of freedom is reflected in simple parameters
of the evolution equations, for example, friction coefficients, reaction rates, or
viscosities, so that one gets in fact the impression of a deterministic motion
of the relevant degrees of freedom. The condition for the applicability of such
deterministic evolution equations are obviously small values of the so-called
diffusion coefficients B
αβ
and the transition rates W (Y | Z; t).
To demonstrate the validity of (6.97) we point out first that for t = t
the
initial conditions (6.99) lead to P (X, t
| Z, t
)=δ (X − Z). The proof of all
other times is best obtained by direct substitution. We see that
dP (X, t | Y,t
)
dt
= −
α
∂
∂X
α
δ
X −
X(t)
d
X
α
(t)
dt
= −
α
∂
∂X
α
δ
X −
X(t)
F
α
(
X(t),t)
= −
α
∂
∂X
α
[F
α
(X, t)P (X, t | Y,t
)] (6.100)
leads to the expected identity. It should be remarked that the methods of
characteristics can be used to obtain (6.98)from(6.96) in a direct way.
6.7.3 Markov Diffusion Processes
If we assume the quantities W (X | Z; t) to be zero, the differential Chapman–
Kolmogorov equation reduces to the so-called Fokker–Planck equation [2]
3
For example, an excellent mechanical construction of a pendulum also cannot
avoid the occurence of weak friction effects.

6.7 Generalized Fokker–Planck Equation 175
∂
∂t
p (X, t | Y,t
)=−
α
∂
∂X
α
F
α
(X, t)p (X, t | Y,t
)
+
αβ
1
2
∂
2
∂X
α
∂X
β
D
αβ
(X, t)p (X, t | Y,t
) . (6.101)
The functions F
α
(X, t) are the components of the drift vector and the
D
αβ
(X, t) are known as components of the diffusion matrix. As mentioned
above, the diffusion matrix is symmetric and positive semi-definite as a result
of definition (6.79). All processes which can be described by an equation of
type (6.101) are called Markov diffusion processes.
The general solution of this differential equation cannot be given explicitly.
However, we can use certain similarities in the mathematical structure of the
Fokker–Planck equation and the Schr¨odinger equation of quantum mechanics
in order to transfer well-known solution methods.
But there are some important differences between both equations, which
have to do with the operator structure of the right-hand side. Each Schr¨odinger
equation always requires a self-adjoint but not necessarily positive definite
operator while the differential operator of a Fokker–Planck equation must be
positive semi-definite, but not self-adjoint. In the case of constant compo-
nents F
α
and B
αβ
, the Fokker–Planck equation (6.101) can be solved exactly,
subject to the initial condition (6.92), and we arrive at
p (X, t | Y,t
)=
1
det(2πD∆t)
exp
−
1
2∆t
αβ
∆X
α
D
−1
αβ
∆X
β
(6.102)
with ∆X
α
= X
α
−Y
α
−F
α
∆t, ∆t = t − t
,andN the dimension of the state
space. That is nothing but a multivariable Gaussian probability distribution
function. The initial condition appears for ∆t → 0 while the Gaussian spreads
over the whole space for ∆t →∞. The center of the Gaussian moves with the
constant velocity F.
6.7.4 Jump Processes
Finally we consider the case F
α
= D
αβ
=0.Wenowhave
∂
∂t
p (X, t | Y,t
)=H
dZW (X | Z; t) p (Z, t | Y,t
)
−H
dZW (Z | X; t) p (X, t | Y, t
) . (6.103)
This is a so-called Master (or rate) equation. The initial condition of this
equation is again given by (6.92). In order to discuss the underlying processes
described by master equations we solve (6.103) approximately in first order
to a small time interval δt. The short-time solution to this equation with the
initial condition (6.92)is
