Schulz M. Control Theory in Physics and Other Fields of Science: Concepts, Tools, and Applications
Подождите немного. Документ загружается.


7.1 Markov Diffusion Processes under Control 197
p ([X]) =
DQ exp
i
T
0
dtQ(t)
˙
X(t) − F (X(t),t)
× exp
−
1
2
T
0
dtQ(t)D(X(t),t)Q(t)
(7.11)
with the integral measure
DQ = lim
M→∞
M
2
j=1
d
N
Q(t
j
)
(2π)
N
. (7.12)
From a mathematical point of view, (7.11) is only a symbolic representation
of (7.10). A concrete determination of the quantity p([X]) always requires the
consideration of the quasi-discrete formulas (7.10). On the other hand, (7.11)
is very helpful for the study of general properties of a stochastic processes,
the introduction of graph theoretical formulations of a suitable perturbation
theory, and renormalization group approaches [4, 6, 10].
7.1.3 Performance
We assume, as in Sect. 2.2.1, that the aim of a stochastic control is also defined
by a functional which should be minimized to obtain the optimum control.
Since the three different types of control aim, namely, integral functionals,
endpoint functionals, and mixed forms can be transformed into each other,
we consider only integral functionals as the control aim.
This functional is, similar as (2.52), given by the trajectory X(t), the
control u(t), and the control horizon T . In the case of a deterministic con-
trol, the constraints, i.e., the equations of motion, the boundary conditions
(X(0) = X
0
and X(T )=X
e
), and the control law u(t) define completely the
trajectory of the system. Therefore, it would be possible to compute a unique
solution of the equations of motion, X(t, u, X
0
,X
e
), for an arbitrary control,
but fixed boundary conditions and insert this solution in the performance
integral (2.52). We obtain the performance along an admissible trajectory
R [X, u, T ] →
R[X
0
,X
e
,u,T]=
T
0
dtφ(t, X(t, u, X
0
,X
e
),u(t)) . (7.13)
The minimization of
R[X
0,
X
e
,u,T] with respect to all admissible control func-
tions u(t) then yields the wanted optimal control u
∗
(t). In the case of a sto-
chastic process, one must be more careful. The solution of the equations of
motion (6.155) also depends on the concrete realizations of the Wiener process
while the end condition is mostly chosen to be free. Thus, we now get
R[X
0,
X
e
,u,T] →
R[u, X
0,
W, T ]=
T
0
dtφ(t, X(t, u, W, X
0
),u(t)) , (7.14)

198 7 Optimal Control of Stochastic Processes
and the performance integral
R[u, X
0,
W, T ] is now a stochastic quantity.
Therefore, it is necessary to average over all realizations of the Wiener process.
The simplest requirement for an optimal stochastic control is
J(X
0
,u,T)=
R[u, X
0,
W, T ]
W
→ inf , (7.15)
where the average is taken over all Wiener processes considering the applied
control mechanism
4
. However, the average procedure includes another impor-
tant uncertainty. The minimization of the deterministic performance integral
(7.13) with respect to the control function can be transformed into the mini-
mization and maximization, respectively, of
Φ
+
R[X
0,
X
e
,u,T]
→ inf (7.16)
and
Φ
−
R[X
0,
X
e
,u,T]
→ sup (7.17)
with an arbitrary monotonously increasing function Φ
+
and an arbitrary
monotonously decreasing function Φ
−
, respectively, without a change of the
optimal control. This is not the case in the stochastic optimization. The op-
timum problems
Φ
+
R[u, X
0,
W, T ]
W
→ inf (7.18)
and
Φ
−
R[u, X
0,
W, T ]
W
→ sup (7.19)
now depend on the chosen functions Φ
+
and Φ
−
. This may be illustrated by
a simple example. Let us consider a certain one-component control leading to
the stochastic performance
R[u, X
0,
W, T ]=
T
0
u
2
(t)dt +[W (T ) − W (0)]
T
0
(1 + u(t))
2
dt
1/2
. (7.20)
Then we get for the average over the whole control period
R[u, X
0,
W, T ]
W
=
T
0
u
2
(t)dt (7.21)
and consequently the optimal control u
∗
(t) = 0, while the minimization of
4
This means that in the case of an open loop control, the complete realizations of
the Wiener process over the period [0,T] are taken into account while a feedback
control requires at a certain time t>0 only the average over the future period
[t, T ].

7.2 Optimal Open Loop Control 199
exp
R[u, X
0,
W, T ]
W
=exp
T
0
u
2
(t)dt +
T
2
T
0
(1 + u(t))
2
dt
(7.22)
and the optimal control is now given by u
∗
(t)=−T/(2 + T ).
7.2 Optimal Open Loop Control
7.2.1 Mean Performance
The open loop control requires that the controller has no information about
the stochastic evolution of the driving terms during the whole control pe-
riod, which means that the optimal control must be a deterministic function
of time obtainable from the knowledge of the functional structure about the
drift terms and about the diffusion coefficients of the underlying Markov dif-
fusion process. In other words, we now consider the Ito stochastic differential
equation
dX(t)=F (X(t),u(t),t)dt +
R
k=1
d
k
(X(t),u(t),t)dW
k
(t) (7.23)
with the N-dimensional state vector X,then-component control function
u(t), and R independent realizations of the Wiener process. This is a typi-
cal case for physical experiments. An accurate preparation of the initial state
X(0), the complete knowledge of the deterministic drift terms F, but incom-
plete information about the stochastic parts
5
, is a standard situation for sev-
eral physical experiments on mesoscopic scales. Typical examples are tracer
diffusion experiments in liquids and amorphous solids where the diffusive par-
ticles are not observable during a certain period. An open loop control of such
a system is, for example, the induced localization of the particles by external
fields close to their injection points under a sufficiently small disturbance of
the liquid or solid environment.
The stochastic Ito differential equation (7.23) under control is equivalent
to the Fokker–Planck equation
∂
∂t
p (X, t | X
,t
)=
1
2
α,β
∂
2
∂X
α
∂X
β
[B
αβ
(X, u(t),t)p (X, t | X
,t
)]
−
α
∂
∂X
α
[F
α
(X, u(t),t)p (X, t | X
,t
)] . (7.24)
Both equations, (7.23) and (7.24), correspond to the formal path integral
5
Only the coupling functions b
k
between the noise terms dW
k
and the system are
well known.

200 7 Optimal Control of Stochastic Processes
p ([X]) =
DQ exp
i
T
0
dtQ(t)
˙
X(t) − F (X(t),u(t),t)
exp
−
1
2
T
0
dtQ(t)D(X(t),u(t),t)Q(t)
(7.25)
representing the weight of a certain stochastic trajectory of the system through
the phase space. In order to complete the problem, we introduce the initial
condition X(0) = X
0
, while the final position should be open. Finally we have
to choose the performance. Here, we use the representation
J[X
0
,u,T]=exp
−
T
0
dtφ(t, X(t),u(t))
X(0)=X
0
. (7.26)
The average is taken with respect to the external noise. The control aim
requires that the averaged performance should become a maximum. The main
problem is now to calculate this average. To this aim we consider that p ([X])
is the statistical weight of a certain admissible trajectory. Thus,
J[X
0
,u,T]=
DX exp
−
T
0
dtφ(X(t),u(t),t)
p[X] (7.27)
with
DX = lim
M→∞
M
2
j=1
d
N
X(t
j
) . (7.28)
We remark that this integral measure must be understood with respect to the
time discrete representation used in (7.10). Inserting (7.25)in(7.27), one get
the mean performance
J[X
0
,u,T]=
DXDQ exp {−S [X, Q, u, T ]} (7.29)
with the action
S [X, Q, u, T]=
T
0
dtL (X(t),Q(t),u(t),t) (7.30)
and the Lagrangian
L (X(t),Q(t),u(t),t)=φ(X(t),u(t),t)+
1
2
Q(t)D(X(t),u(t),t)Q(t)
−iQ(t)
˙
X(t) − F (X(t),u(t),t)
(7.31)
corresponding to the language used in Chap. 2. In this sense, the ‘ghost’
variables

7.2 Optimal Open Loop Control 201
P (t)=
∂L
∂
˙
X(t)
= −iQ(t) (7.32)
are called the generalized momenta. Furthermore, the integral (7.29)canbe
interpreted as taken over the whole generalized phase space P ×
P formed by
the phase space
6
P and the adjoint phase space P corresponding to the set of
all admissible momenta P(t).
The remaining problem is the calculation of the optimum control law.
The standard way is the evaluation of (7.29) by the Laplace method [3]. This
method is sometimes referred to as ‘steepest descent’. But this terminology is
inadequate for the present case. The idea is very simple. We first determine a
provisional optimal control, given by u
∗
,
X
∗
,and
Q
∗
(or
P
∗
), which minimizes
the action S [X, Q, u,T ]. Then we expand the action around this so-called tree
approximation
S [X, Q, u, T]=S
X
∗
,
Q
∗
, u
∗
,T
+ ∆S
ξ,η, ω,
X
∗
,
Q
∗
, u
∗
,T
(7.33)
with ξ = X −
X
∗
, η = Q −
Q
∗
,andω = u − u
∗
. The integral (7.29)now
becomes
J[X
0
,u,T] = exp
,
−S
X
∗
,
Q
∗
, u
∗
,T
-
×
DξDη exp
,
−∆S
ξ,η, ω,
X
∗
,
Q
∗
, u
∗
,T
-
. (7.34)
The leading contributions to the performance are often determined by the
first term in (7.34) while the integral yields only some corrections. If these
corrections cannot be neglected, the last step is the determination of the
hopefully small contributions ω
∗
which maximize the performance J[u, X, T ].
Then, the desired optimal control is given by u
∗
= u
∗
+ω
∗
. The determination
of ω
∗
requires the explicit computation of the second term of (7.34). This can
be done by various special techniques which one can find in the widespread
literature [4, 5, 6]. The presentation of these, partially very powerful, methods
goes beyond the scope of this book.
We remark that, however, the calculation of the tree approximation is
often a sufficient approach to estimate the optimal control.
7.2.2 Tree Approximation
The above-mentioned provisional optimal control follows directly from the
application of the variational principle, discussed in Chap. 2. Hence, we can
follow the concept presented there. The Lagrangian (7.31) yields the follow-
ing Euler–Lagrange equations. The first group corresponds to the evolution
equations of the optimum trajectory
˙
X
∗
= F (
X
∗
, u
∗
,t)+D(
X
∗
, u
∗
,t)
P
∗
, (7.35)
6
For the sake of simplicity we assume P = R
N
.

202 7 Optimal Control of Stochastic Processes
where we have introduced the N -component momentum state
P
∗
(t)=
−i
Q
∗
(t), see (7.32). The second group of equations is given by
˙
P
∗
=
∂
∂
X
∗
φ(
X
∗
, u
∗
,t) −
1
2
P
∗
D(
X
∗
, u
∗
,t)
P
∗
− F (
X
∗
, u
∗
,t)
P
∗
(7.36)
while the last group reads
∂
∂u
∗
φ(
X
∗
, u
∗
,t)=
1
2
∂
∂u
∗
P
∗
D(
X
∗
, u
∗
,t)
P
∗
+2
P
∗
F (
X
∗
, u
∗
,t)
. (7.37)
These equations are completed by the initial conditions
X
∗
(0) = X
0
and
Q
∗
(T )=0, (7.38)
which can be obtained following the same considerations as in Sect. 2.4.1.
The equations (7.35), (7.36), and (7.37) are the tree approach to the above-
introduced open loop stochastic control problem. Although these equations
are similar to the optimal control equations (2.70), (2.74), and (2.75) for the
deterministic control problem, there are some essential differences:
• The main difference is that the control law, u
∗
(t), is only an approxima-
tion for the optimal control of the stochastic problem which considers the
fluctuations due to the stochastic sources only on a mean field level. We
remark, that in case of D → 0, i.e. in case of vanishing noise terms, the
evolution equations (7.35), (7.36), and (7.37) converge to (2.74), (2.70),
and (2.75) and, furthermore, the provisional optimal control law u
∗
(t)ap-
proaches the optimal control law u
∗
(t).
• The second difference belongs to the meaning of the optimal trajectory
X
∗
(t). While X
∗
(t) of the deterministic problem corresponds to the tra-
jectory of the system through the phase space in the case of an optimal
control, the trajectory
X
∗
(t) is at best an estimation of the averaged tra-
jectory in the case of an optimal control of the stochastic problem.
• The third problem comes from the fact that the Lagrangian is now a
complex quantity. But this problem is only an apparent one.
In order to demonstrate that the complex character of the Lagrangian is
not very dangerous, we consider again (7.29) together with (7.30) and (7.31)
and execute the integration over Q. Then we obtain
J[X
0
,u,T]=
DX exp
$
−S [X, u, T]
%
Det
−1/2
D (7.39)
with the reduced action
S [X, u, T ]=
T
0
dtL (X(t),u(t),t) (7.40)
and the corresponding real-valued Lagrangian
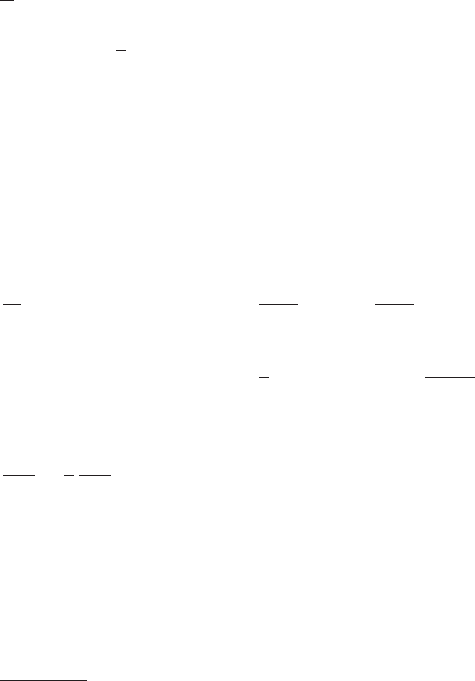
7.2 Optimal Open Loop Control 203
L (X, u, t)=φ(X,u, t)
+
1
2
˙
X −F (X, u, t)
D
−1
(X, u, t)
˙
X −F (X, u, t)
. (7.41)
Furthermore, we have used the abbreviation
DetD = lim
M→∞
M−1
2
j=0
(2πδt)
N
det D(X(t
j
),u(t
j
),t
j
)
. (7.42)
Note that this path determinant is not considered in the tree approximation
but in the subsequent harmonic approach and the perturbation theory. Thus,
we get the Euler–Lagrange equations in the tree approximation, namely
d
dt
N
β=1
D
−1
αβ
˙
X
∗
β
− F
β
=
∂φ
∂
X
∗
α
−
N
β,γ=1
∂F
β
∂
X
∗
α
D
−1
βγ
˙
X
∗
γ
− F
γ
+
1
2
N
β,γ=1
˙
X
∗
β
− F
β
∂D
−1
βγ
∂
X
∗
α
˙
X
∗
γ
− F
γ
(7.43)
and
∂φ
∂u
∗
+
1
2
∂
∂u
∗
˙
X −F
D
−1
˙
X −F
=0. (7.44)
In order to avoid confusion we have used the component representation in
(7.43). Readers may check themselves that both equations are also obtainable
from (7.35), (7.36), and (7.37) by elimination of the momenta. Another im-
portant property follows for vanishing diffusion coefficients, D → 0. In this
case, the integration of (7.29) with respect to Q considering (7.30) and (7.31)
leads to
R[u, X, T ]=
DX exp
−
T
0
dtφ(X(t),u(t),t)
×
'
δ
˙
X(t) − F (X(t),u(t),t)
(7.45)
with the formal representation
'
δ
˙
X(t) − F (X(t),u(t),t)
= lim
M→∞
M−1
2
j=0
δ (X(t
j+1
) − X(t
j
) − F (X(t
j
),t
j
)δt) . (7.46)
Thus, in case of B → 0, relation (7.45) is equivalent to the performance
J[X
0
,u,T] = exp
−
T
0
dtφ(X
S
(t),u(t),t)
(7.47)

204 7 Optimal Control of Stochastic Processes
along the solution X
S
(t) of the evolution equation
˙
X = F (X, u, t) but without
solving this equation explicitly. Obviously, the exponent of (7.47) is nothing
but the deterministic performance integral (7.13) with free end conditions,
which means that the open loop stochastic control converges as expected for
vanishing diffusion coefficients to the deterministic open loop control. In this
special case, the tree approximation becomes a rigorous result. But this state-
ment also means that the tree approach becomes a reasonable approximation
for small diffusion coefficients, i.e., for small stochastic perturbations of the
system.
Finally, we remark that the Hamilton representation, discussed in
Sect. 2.4.2, and the Pontryagin’s maximum principle, see Sect. 2.4.3, can also
be extended to the tree approximation of the stochastic control problem.
There also exist other approaches to the open loop control problem. A
popular alternative method is the expansion of the optimal performance and
the control functions in powers of small noise terms [7, 8] or the method of
stochastic integration [9].
7.3 Feedback Control
7.3.1 The Control Equation
Now we consider the situation that the controller has information about the
current state and the history, but not about the future evolution of the sto-
chastic terms. This is a typical feature of a feedback control. In the literature,
two general types of feedback control are discussed [11, 12, 13]. We speak
about a complete observation if the controller has the full information of the
current state X(t) and its history. Otherwise, if the controller have only in-
formation about the history and the current values of a certain ‘observable’
part of the state, we denote this situation as the case of partial observation. In
the following we focus mainly on the complete observation case, while partial
observations will be considered in the subsequent chapters.
We suppose that the current time is τ. As a criterion to be minimized
we now use the expected value of the future performance with respect to the
current initial state X(τ )=Y .Thus(7.15) has now the concrete form
J[Y, τ,u,T]=
T
τ
dt φ(t, X(t),u(t))
X(τ )=Y
=
T
τ
dt
dXφ(t, X, u(t))p
u
(X, t | Y,τ) , (7.48)
where we have supposed that each feedback control u corresponds to a tran-
sition probability p
u
(X, t | Y,τ) from the state Y at time τ to the state X
at time t considering the presence of the control law u. The characteristic
structure of the feedback control applied at time t is given by
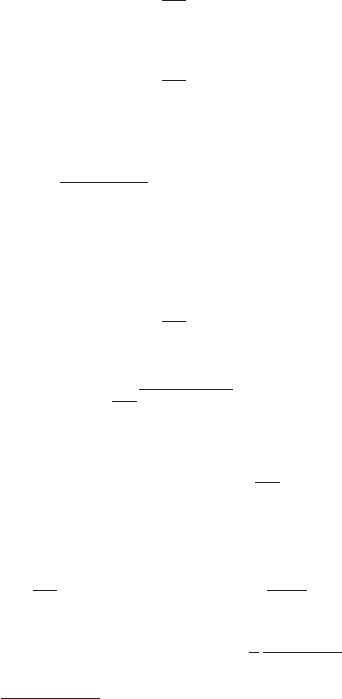
7.3 Feedback Control 205
u(t)=u(t, X(t)) . (7.49)
The aim of an optimal feedback control is now to minimize the conditionally
averaged performance J[Y,τ,u, T]. Let us assume that
V (Y,τ, T) = min
u
J[Y, τ,u,T] . (7.50)
Thus, an optimal feedback control law u
∗
has the property that
V (Y,τ, T)=J[Y, τ,u
∗
,T] . (7.51)
In order to obtain an equation for V (Y,τ, T) we use the following identity:
t
τ
dt
dX
∂
∂t
[V (X, t
,T)p
u
(X, t
| Y,τ)]
=
dX
t
τ
dt
∂
∂t
[V (X, t
,T)p
u
(X, t
| Y,τ)]
=
dX V (X, t, T )p
u
(X, t | Y,τ) −
dX V (X, τ, T )p
u
(X, τ | Y,τ)
=
V (X, t, T)
X(τ )=Y,u
− V (Y, τ,T) , (7.52)
where we have used P (X, τ | Y,τ)=δ(X −Y ); see (6.92). On the other hand,
we obtain from the left-hand side
t
τ
dt
dX
∂
∂t
[V (X, t
,T)p
u
(X, t
| Y,τ)]
=
t
τ
dt
∂
∂t
V (X, t
,T)
X(τ )=Y,u
+
t
τ
dt
dXV (X, t
,T)
∂
∂t
p
u
(X, t
| Y,τ) . (7.53)
The second term can be rewritten using the Fokker–Planck equation
7
(6.101)
∂
∂t
p
u
(X, t
| Y,τ)=−
α
∂
∂X
α
F
α
(X, u, t
)p
u
(X, t
| Y,τ)
+
αβ
1
2
∂
2
∂X
α
∂X
β
D
αβ
(X, u, t
)p
u
(X, t
| Y,τ) (7.54)
7
We remark that the same procedure can also be carried out for the general case of
a differential Chapman–Kolmogorov equation. In this case, the optimal stochastic
control equation considers not only the diffusive Wiener processes but also also
jump processes.

206 7 Optimal Control of Stochastic Processes
Thus, we obtain for the second term of (7.53)
(2) = −
α
t
τ
dt
dXV (X, t
,T)
∂
∂X
α
[F
α
(X, u, t
)p
u
(X, t
| Y,τ)]
+
1
2
αβ
t
τ
dt
dXV (X, t
,T)
×
∂
2
∂X
α
∂X
β
[D
αβ
(X, u, t
)p
u
(X, t
| Y,τ)]
=
α
t
τ
dt
dX
∂
∂X
α
V (X, t
,T)
F
α
(X, u, t
)p
u
(X, t
| Y,τ)
+
1
2
αβ
t
τ
dt
dX
∂
2
∂X
α
∂X
β
V (X, t
,T)
× D
αβ
(X, u, t
)p
u
(X, t
| Y,τ) , (7.55)
where we have obtained the last expression by integration by parts. Using the
so-called backward Focker–Planck operator
'
F (X, u, t)=
α
F
α
(X, u, t)
∂
∂X
α
+
1
2
αβ
D
αβ
(X, u, t)
∂
2
∂X
α
∂X
β
, (7.56)
we obtain
(2) =
t
τ
dt
dX
'
F (X, u, t
)V (X, t
,T)
p
u
(X, t
| Y,τ)
=
t
τ
dt
'
F (X, u, t
)V (X, t
,T)
X(τ )=Y,u
. (7.57)
Inserting this expression in (7.53) we arrive at
t
τ
dt
dX
∂
∂t
[V (X, t
,T)p
u
(X, t
| Y,τ)]
=
t
τ
dt
∂
∂t
V (X, t
,T)
X(τ )=Y,u
+
t
τ
dt
'
F (X, u, t)V (X, t
,T)
X(τ )=Y,u
(7.58)
and (7.52) can be rewritten as
