Schulz M. Control Theory in Physics and Other Fields of Science: Concepts, Tools, and Applications

Подождите немного. Документ загружается.

186 6 Nonequilibrium Statistical Physics

of the ﬂuctuation forces into bilinear combinations of independent stochastic

functions η

(t) which are assumed to be exclusively controlled by the dy-

namics of the irrelevant degrees of freedom and systematic terms

α,k



(∂G

/∂X

β,k

controlled by the relevant quantities, and the state vec-

tor, respectively, is a natural ansatz, which is not in disagreement with the

requirements of the projection formalism.

It should be noticed that (6.146) is only an obvious assumption, which

is perhaps supported by empirical experience. Equation (6.146) cannot be

generally derived so far in the framework of a closed theory.

As mentioned above, the Markov approximation (6.133) requires

(t)f



) ∼ δ(t − t



)and

(t)=0. (6.147)

This δ-function character is also transferred to the stochastic functions η

(t).

In general, we are able to specify the stochastic functions to

(t)η





)=δ



δ(t − t



) and ¯η

(t) = 0 (6.148)

by a suitable choice of the functions

α,k

(X)in(6.146).

Let us return to the discussion of the stochastic diﬀerential equation

(6.144). Unfortunately, this equation as it stands has no meaning, and we

do not know how to deal with it. The reason is that the δ-character of the

correlation functions (6.148) causes jumps in the state vector X(t) such that

the value of X(t) at time t is not well deﬁned. Basically, the problem arises

from the fact that the stochastic functions η

(t) change substantially during

an inﬁnitesimally small time interval so that the equation does not specify

what value of d

α,k

(X) should be used in the product d

α,k

(X(t))η

(t).

For a better understanding of the problem, we divide the time axis into

inﬁnitesimally small subintervals of length dt by means of partitioning points

with t

i+1

= t

+dt and deﬁne intermediate points τ

such that t

<τ

i+1

Then we obtain from (6.144)

i+1

)=X

)+F

(X(t

))dt +



k=1

i+1



α,k

(X(t



))η



)dt



(6.149)

or due to the mean value theorem

i+1

)=X

)+F

(X(t

))dt +



k=1

α,k

(X(τ

))

i+1





)dt



. (6.150)

The main problem comes from the integral

i+1





)dt



. (6.151)

It is easy to see that the application of (6.148) leads to

6.9 Stochastic Equations of Motions 187

)dW



)=δ



dt and dW

)=0. (6.152)

This is nothing but the mean and the correlation of inﬁnitesimal changes

of independent Wiener processes W

(t)(k =1,...,R). Now we can rewrite

(6.150) to obtain

i+1

)=X

)+F

(X(t

))dt +



k=1

α,k

(X(τ

))dW

) . (6.153)

However, we can evaluate d

α,k

(X(τ

)) at an arbitrary intermediate time τ

.It

is clear that the choice of this intermediate time has important consequences

for numerical simulations of stochastic processes. Two general concepts were

established.

In the Ito interpretation [1, 16], the value of X(τ

) in taken before the

jump. That means explicitly

i+1

)=X

)+F

(X(t

))dt +



k=1

α,k

(X(t

))dW

) (6.154)

or in the time-continuous notation

(t)=F

(X(t))dt +



k=1

α,k

(X(t))dW

(t) . (6.155)

On the other hand, in the Stratonovich interpretation [13, 16], we take the

mean of X(t) before and after the jump so that X(τ

)=(X(t

i+1

)+X(t

))/2,

i.e.,

i+1

)=X

)+F

(X(t

))dt



k=1

α,k



X(t

)+X(t

i+1

)



) . (6.156)

The time-continuous representation of the Stratonovich stochastic diﬀerential

equation now reads

(t)=F

(X(t))dt +



k=1

α,k



X(t)+

dX(t)



(t) . (6.157)

Neglecting dX(t) on the right-hand side of (6.157) one apparently obtains

the same time-continuos notation as (6.155). This constitutes a warning that

both representations are identical. That is always not the case. A solution of

the Ito stochastic diﬀerential equation (6.155) with given F

and d

α,k

is not

a solution of the same equation with the same coeﬃcients, but interpreted to

be of the Stratonovich type. However, both solutions become identical if the

coeﬃcients of an Ito stochastic diﬀerential equation

= F

Ito

(X)dt +



k=1

Ito

β,k

(X)dW

(6.158)

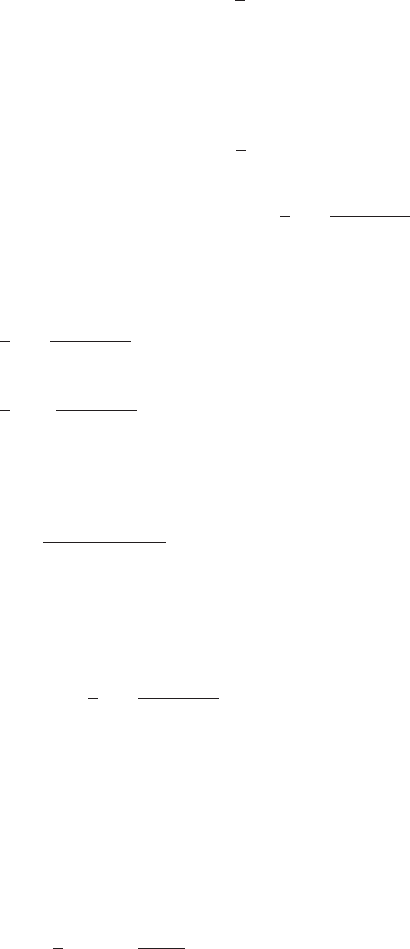
188 6 Nonequilibrium Statistical Physics

are related to the coeﬃcients of a Stratonovich stochastic diﬀerential equation

= F

(X)dt +



k=1

α,k



X +



(6.159)

by a certain transformation. To ﬁnd this relation, we expand the Stratonovich

representation up to the ﬁrst order in dX(t) and consider that X(t)isalsoa

solution of (6.158):

= F

(X)dt +



α,k



X +



= F

(X)dt +



α,k

(X)dW



k,β

∂d

α,k

(X)

∂X

= F

(X)dt +



α,k

(X)dW



k,β

∂d

α,k

(X)

∂X

Ito

(X)dtdW



k,j,β

∂d

α,k

(X)

∂X

Ito

β,j

(X)dW

. (6.160)

Considering dW ∼ dt

1/2

, the third term is of order dt

3/2

and can be neglected.

But the last term contains dW

∼ dt and, therefore, it must be taken

into accout. We use the splitting

= dW

(t)dW

(t)+dϕ

(t) . (6.161)

Since dW

is of order dt, but dW

is of order dt

1/2

, the ﬂuctuations of

can be neglected compared with the ﬂuctuations of dW

.Thusit

remains the systematic part and we obtain with (6.152)





(X)+



k,β

∂d

α,k

(X)

∂X

Ito

β,k

(X)





dt +



α,k

(X)dW

. (6.162)

A comparison of (6.162) with (6.158) leads to the desired transformations be-

tween the coeﬃcients of Ito stochastic diﬀerential equations and Stratonovich

stochastic diﬀerential equations describing the same process. We obtain con-

ditions

α,k

= d

Ito

α,k

(6.163)

and

= F

Ito

−



β,k

Ito

β,k

∂d

Ito

α,k

∂X

(6.164)

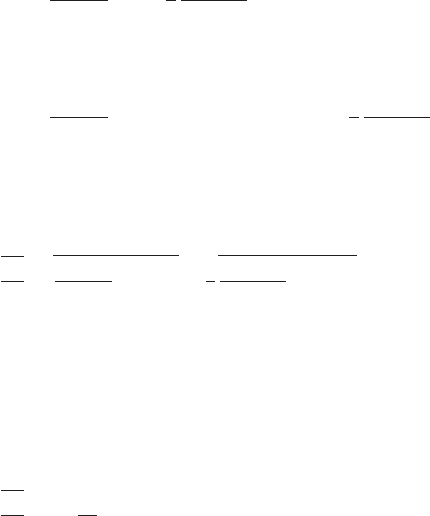
6.9 Stochastic Equations of Motions 189

Finally we remark that independently of the interpretation of the stochastic

diﬀerential equation (6.144), the coeﬃcients F

(X)andd

α,k

(X) can be ex-

tended to explicitly time-dependent functions F

(X, t)andd

α,k

(X, t). Such

an extension is motivated above all by the fact that possibly a part of the

irrelevant variables possesses relatively slow time scales in the order of the

magnitude of the characteristic time of the relevant quantities.

6.9.5 Ito’s Formula and Fokker–Planck Equation

Let us consider an arbitrary diﬀerentiable function f(X) where X = X(t)is

the solution of the Ito stochastic diﬀerential equation (6.154). For the sake

of simplicity we consider only one relevant degree of freedom and only one

Wiener process. Then the Ito diﬀerential equation reads

dX = F (X, t)dt + d(X, t)dW(t) . (6.165)

The diﬀerential df is deﬁned as

df = f (X(t +dt)) − f (X(t)) = f(X +dX) − f(X) . (6.166)

We expand (6.166) to second-order in dX

df =

∂f(X)

∂X

dX +

∂

f(X)

∂X

+ o





(6.167)

and replace dY by (6.165). Considering again dW ∼ dt

1/2

,weexpand(6.167)

up to ﬁrst order in dt

df =

∂f(X)

∂X

[F (X, t)dt + d(X, t)dW ]+

∂

f(X)

∂X

[b(X, t)dW ]

, (6.168)

where all other terms have been discarded since they are of higher order. This

relation is known as Ito’s formula.

Now we perform the average with respect to all realizations of the Wiener

process W (t) and obtain

∂f(X)

∂X

F (X, t)+

∂

f(X)

∂X

(X, t) . (6.169)

For the determination of the averages we used the Ito calculus, especially

(6.152) and the property that the value of X(t) is taken before the jump

dW (t). The last remark means that the actual value of X(t) and the value of

the subsequent jump dW (t) are statistically independent.

On the other hand, X(t) has the conditional probability density p (X, t|X



If the evolution starts from the initial state X(t



)=X



, then the averages are

given by



∂

∂t

p (X, t | X



) f(X)dX (6.170)

and

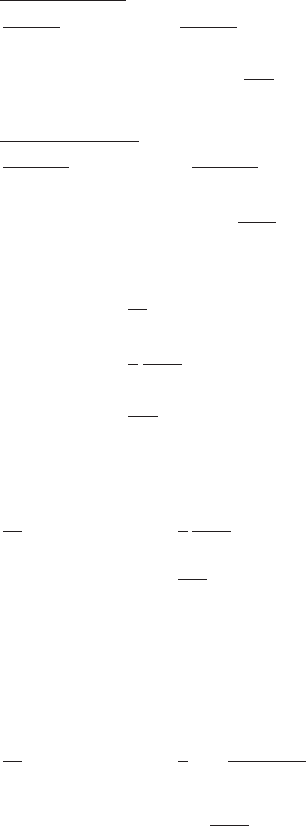
190 6 Nonequilibrium Statistical Physics

∂f(X)

∂X

F (X, t)=



∂f(X)

∂X

F (X, t)p (X, t | X



)dX

= −



f(X)

∂

∂X

[F (X, t)p (X, t | X



)] dX (6.171)

and

∂

f(X)

∂X

(X, t)=



∂

f(X)

∂X

(X, t)P (X, t | X



)dX



f(X)

∂

∂X



(X, t)P (X, t | X



)



dX. (6.172)

Putting all these results together and integrating by parts, we arrive at



dXf(X)

∂

∂t

p (X, t | X



)



dXf(X)

∂

∂X



(X, t)p (X, t | X



)



−



dXf(X)

∂

∂X

[F (X, t)p (X, t | X



)] . (6.173)

Now we consider that we have chosen the function f (X) to be arbitrary.

Hence, we conclude that the conditional probability satisﬁes the equation

∂

∂t

p (X, t | X



∂

∂X



(X, t)p (X, t | X



)



−

∂

∂X

[F (X, t)p (X, t | X



)] . (6.174)

Obviously, we get a complete equivalence between the stochastic diﬀerential

equation (6.165) and the Fokker–Planck equation (6.174). This result can be

generalized for the case of a system of N stochastic diﬀerential equations with

R Wiener processes. The set of diﬀerential equations may be given by (6.144).

The corresponding Fokker–Planck equation then reads

∂

∂t

p (X, t | X





α,β

∂

∂X

αβ

(X, t)p (X, t | X



)] (6.175)

−



∂

∂X

(X, t)p (X, t | X



)] (6.176)

with

αβ

(X, t)=



k=1

α,k

(X, t)d

β,k

(X, t) . (6.177)

A similar connection between the Stratonovich stochastic diﬀerential equa-

tions and the corresponding Fokker–Planck equation can be obtained by ap-

plication of the converting rules (6.164) and (6.163). Thus, the system of

stochastic diﬀerential equations (6.144) in the Stratonovich interpretation is

related to the Fokker–Planck equation

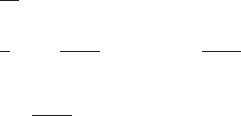
References 191

∂

∂t

p (X, t | X



)



α,β,k

∂

∂X



α,k

(X, t)

∂

∂X

β,k

(X, t)p (X, t | X



))



−



∂

∂X

(X, t)p (X, t | X



)] . (6.178)

Finally it should be noticed that the connection between the stochastic diﬀer-

ential equations and Fokker–Planck equations allows us to create representa-

tive trajectories for a given Fokker–Planck equation by numeric simulations.

References

1. L. Arnold: Stochastic Diﬀerential Equations (Wiley-Interscience, New York,

1974) 187

2. H. Risken: The Fokker–Planck Equation (Springer, Berlin Heidelberg New York,

1984) 174

3. E. Fick, G. Sauermann: Quantenstatistik DYNAMISCHER Prozesse I (Akadem-

ische Verlagsgesellschaft, Leipzig, 1983) 150, 160

4. E.Fick,G.Sauermann:Quantenstatistik Dynamischer Prozesse IIa (Akademis-

che Verlagsgesellschaft, Leipzig, 1983) 150, 167, 180

5. M. Schulz: Statistical Physics and Economics (Springer, Berlin Heidelberg New

York, 2003) 160, 182

6. W. G¨otze,L.Sj¨ogren; J. Non-Cryst. Solids 131–133, 161 (1991) 160

7. W. G¨otze,L.Sj¨ogren, Rep. Prog. Phys. 55, 241 (1992) 160

8. K. Kawasaki: Ann. Phys. 61, 1 (1970) 160

9. W. G¨otze, A. Zippelius: Phys. Rev. A 14, 1842 (1976) 182

10. J. Marcienkiewicz: Math. Z. 44, 612 (1939) 164

11. C.W. Gardiner: Handbook of Stochastic Methods (Springer, Berlin Heidelberg

New York, 1997) 169

12. U. Balucanu, M. Zoppi: Dynamics of the Liquid State (Clarendon Press, Oxford,

1994) 167

13. R.L. Stratonovich: Introduction to the Theory of Random Noise (Gordon and

Breach, New York, 1963) 187

14. W. Feller: An Introduction to Probability Theory and Its Applications, vol. 1,

3rd edn (Wiley, New York, 1968) 185

15. W. Feller: An Introduction to Probability Theory and Its Applications, vol. 2,

2nd edn (Wiley, New York, 1971) 185

16. N.G. van Kampen: Stochstic Processes in Physics and Chemistry (North-

Holland, Amsterdam, 1981) 187

17. H. Mori: Prog. Theor. Phys. 33, 423 (1965) 180

18. H. Mori: Prog. Theor. Phys. 34, 339 (1965) 181

19. R. Zwanzig: Ann. Rev. Phys. Chem. 16, 67 (1961) 181

20. A.N. Kolmogorov: Foundations of the Theory of Probability (Chelsa, New York,

1950) 150

Optimal Control of Stochastic Processes

7.1 Markov Diﬀusion Processes under Control

7.1.1 Information Level and Control Mechanisms

Many control problems appearing for complex systems are subject to imper-

fectly known disturbances. As we have learned in the previous chapter, these

disturbances originate by the hidden irrelevant degrees of freedom. Although

we may formally separate the dynamics of relevant and irrelevant variables

into diﬀerent contributions to the equations of motion, see Sect. 1, the time-

dependence of the terms concerning the irrelevant degrees of freedom is still

open. Unfortunately, this problem cannot solved generally, although the Mori–

Zwanzig equations deﬁne a formal expression for the residual forces (6.123).

To proceed, it is necessary to make some approximations about these exist-

ing, but usually ‘a priori’ unknown forces. The simplest, but most common

approach is the Markov approximation discussed in Sects. 6.6 and 6.9.2. This

case allows the introduction and application of the very powerful Ito calculus

or alternatively the use of Fokker–Planck equations in order to describe the

dynamics of the relevant variables driven by external random sources sim-

ulating the eﬀects of the irrelevant degrees of freedom. A large number of

physical processes in complex systems is suﬃciently described by the Markov

approach. As a standard problem we refer to the Brownian motion, originally

observed by Ingenhousz and Brown [1] and ﬁrst described by Einstein [2].

Therefore, we focus in the following mainly on Markov processes.

Let us now assume that we know from experimental investigations or

appropriate assumptions the mathematical structure

of the equations of

The detailed determination of the coeﬃcients a and b of (6.155) is by no means

a simple problem. Usually, one uses an appropriate theoretical model containing

several free parameters. Then, one determines theoretically several moments and

cumulants and compares this with experimentally obtained results. However, this

problem is often hard to handle, especially if the a and b are complicated functions

of the state X.

M. Schulz: Control Theory in Physics and other Fields of Science

STMP 215, 193–212 (2006)

 Springer-Verlag Berlin Heidelberg 2006

194 7 Optimal Control of Stochastic Processes

motion (6.155) describing a stochastically driven process . Then, a control

of this process can be realized under three essentially diﬀerent conditions:

• The controller has no information about the stochastic driving terms dur-

ing the whole control period. In this case he chooses as control a function

of time determined before the control starts. Obviously, this is an open

loop control of a stochastic process.

• The controller has information about the current state and the history,

but not about the future evolution of the stochastic terms. In this case he

reacts onto a current situation. This is a typical closed loop or feedback

control.

• The controller is able to calculate some information about the future evo-

lution of the driving terms from the current state and the history of the

driving terms. In other words, the controller has a partial knowledge about

the intrinsic dynamics of the hidden degrees of freedom of the complex

system. It is clear that under this circumstance, the driving terms are no

longer stochastic in the sense of the Wiener Process. This is a closed loop

foresighted control.

Only the ﬁrst two types of control are related to real Markov processes. Any

predictions which are necessary for the last type of control require the presence

of a memory as discussed in Sects. 6.3.3 and 6.9.1.

7.1.2 Path Integrals

We had already discussed in general that each complex system on the macro-

scopic level can be described by a probabilistic theory. In this sense the prob-

ability distribution function p(X, t) is the central quantity of a quantitative

description. Additionally, as a generalization of p(X,t), we may introduce the

joint probability density p(X

(M)

; X

(M−1)

M−1

; ...; X

(0)

) with M +1

sequenced points in time. The knowledge of this function allows formally the

determination of the probabilistic weight for a trajectory passing the points

(0)

= X(t

)att

, X

(1)

= X(t

)att

, and so on. In this way, we may

interpret the ordered set [X]

= {X(t

),X(t

),...,X(t

M−1

),X(t

)} as a

discrete path which is realized with the probability

p(X

(M)

; X

(M−1)

M−1

; ...; X

(0)

) . (7.1)

Obviously, in the joint probability representation each path is now one possible

event.

Using conditional probabilities, the joint probability for a discrete path of

M + 1 points can be written as follows:

p([X]

)=p



(M)

; ...; X

(0)



= p



(M)

| X

(M−1)

M−1

; ...; X

(0)



× p



(M−1)

M−1

| X

(M−2)

M−2

; ...



7.1 Markov Diﬀusion Processes under Control 195

× p



(1)

| X

(0)





(0)



. (7.2)

Thus the Markov condition, see Sect. 6.5, immediately requires

p([X]) =

M−1

j=0



(j+1)

j+1

| X

(j)



. (7.3)

Setting now t

=0,t

= T , t

= jT/M, and taking the limit M →∞

one obtains the joint probability of a certain trajectory

X(t) of the system

moving from X(0) to X(T )

p([X]) = lim

M→∞

M−1

j=0

p (X(t

j+1

),t

j+1

| X(t

),t

) . (7.4)

In principle, (7.3) is a generalization of the Chapman–Kolmogorov equation

(6.7). The conditional probability p



(j+1)

j+1

| X

(j)



follows from the

solution of the Fokker–Planck equation (6.101) or in general, from the solution

of the diﬀerential Chapman–Kolmogorov equation (6.91). An alternative way

to obtain an explicit expression for this quantity is to write

p (X, t | X







δ (X − X



) p (X



,t| X



)

δ (X − X(t))





. (7.5)

The last expression is the conditional average considering the initial condition

X(t



)=X



of the N-dimensional δ-function

. For inﬁnitesimally small time

periods, δt = t

j+1

− t

= T/M, we obtain from (6.155)

p (X, t | X



)



X −





+ F (X



)δt +



k=1



)dW



)



, (7.6)

where the average is taken with respect to the R independent realizations

of the Wiener process. Note that F and d

are in this representation

N-component vectors, F = {F

,...,F

},andd

= {d

1,k

2,k

,...,d

N,k

The standard Fourier representation of the δ-function yields

Obviously, the trajectory X(t) corresponds to the sequence [X]=[X]

∞

This means that the argument of this function is an N -component vector and the

components contribute to the N-dimensional δ-function as follows

δ(X − Y )=

α=1

δ(X

− Y

) ,

where the δ-function at the right-hand side is the standard Dirac delta function.

196 7 Optimal Control of Stochastic Processes

p (X, t | X





(2π)

× exp



X −





+ F (X



)δt +





)dW



)

;



(2π)

exp





δX

δt

− F (X



)



δt

k=1

exp {−iQd



)dW



)} (7.7)

with δX = X − X



. Considering (6.137), we obtain

exp {−iQd



)dW



)} =



dW exp {−iQd



)(W − W



)}

× p (W, t | W



)



dξ exp {−iQd



)ξ}

√

2πδt

exp



−

2δt

=exp



−



)Qδt

, (7.8)

and therefore with (6.177)

p (X, t | X





(2π)

exp





δX

δt

− F (X



)



δt

exp



−

QD(X



)Qδt

. (7.9)

Inserting this relation into (7.3), one obtains the joint probability p ([X]) for

the realization of a certain path starting in X(0) at t = 0 and ending in X(T )

at t = T :

p ([X]) = lim

M→∞



j=1

Q(t

)

(2π)

× exp









j=1

[Q(t

)(X(t

) − X(t

j−1

)) − Q(t

)F (X(t

j−1

),t

j−1

)δt]







× exp







−



j=1

Q(t

)D(X(t

j−1

),t

j−1

)Q(t

)δt







(7.10)

or symbolically