Сборник докладов - Электроэнергетика глазами молодежи 2010

Подождите немного. Документ загружается.

370

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЛЯ ОЦЕНКИ

ИНВЕСТИЦИОННОЙ ПРИВЛЕКАТЕЛЬНОСТИ

РАСПРЕДЕЛЕННОЙ ГЕНЕРАЦИИ

Т.Ю. Паниковская, Д.А. Чечушков

УрФУ

В настоящее время в России ввод новых генерирующих мощностей отстает от рос-

та электропотребления, кроме того, ситуация усугубляется старением существующих ге-

нерирующих мощностей. Для решения проблемы повышения надежности и безопасности

электроснабжения, сохранения устойчивой работы ЭЭС, а также оптимизации стоимости

электроэнергии для потребителя могут быть предложено следующее:

 ограничение потребления в пиковые часы и смещение нагрузки в непиковую зо-

ну (регулирование нагрузки);

 заключение долгосрочных двусторонних договоров на покупку электроэнергии

и мощности;

 размещение у потребителя источников генерации малой мощности (распреде-

ленной генерации);

 внедрение энергосберегающих технологий производства товаров, услуг.

Некоторые решения могут быть реализованы в краткосрочной перспективе без до-

полнительных инвестиций, а часть невозможно осуществить без значительных финансо-

вых и временных ресурсов.

Одним из наиболее популярных решений является размещение установок распре-

деленной генерации (РГ). В этом случае снижаются риски дефицита мощности и потери

электроснабжения от питающей подстанции основной сети, повышается надежность энер-

госнабжения, улучшаются показатели качества электрической энергии, снижаются потери

мощности и электроэнергии.

Смешанная система электроснабжения обеспечивает дополнение и резервирование

централизованных систем. При этом, например, промышленный потребитель с источни-

ком распределенной генерацией имеет следующие преимущества:

 электрическая и тепловая энергия по стоимости, как правило, ниже установлен-

ных тарифов;

 повышенная надежность энергоснабжения;

 возможность извлечь дополнительные выгоды от продажи тепловой и

электри-

ческой энергии другим потребителям;

 возможность использовать более дешевое местное топливо, что особенно вы-

годно при установке ГТУ, ГТС и ПГУ.

Распределенная генерация позволяет создавать эффективные и надежные системы

производства высококачественной электрической и тепловой энергии в непосредственной

близости от локальных потребителей с учетом их конкретных запросов. Высокая инвести-

ционная привлекательность

и финансовая эффективность распределенных электростанций

обусловлена относительно низким уровнем первоначальных вложений, возможностью

быстрого и поэтапного ввода в эксплуатацию, полным контролем со стороны потребите-

ля, возможностью продажи избыточной электроэнергии. Строительство источников РГ

имеет и системный эффект, так как снижает пиковые нагрузки в целом по энергосистеме.

Возможность и целесообразность строительства источников малой генерации су-

ществовала всегда, как правило, это были небольшие заводские ТЭЦ. Например, для ис-

следуемой территории небольшими станциями покрывается 4–10 % мощности нагрузки.

371

На рисунке 1 представлена диаграмма выработки электроэнергии станциями, имеющими

доступ на оптовый рынок электроэнергии и мощности. Из диаграммы видно, что более

90 % потребления обеспечивается станциями типа ГРЭС, ТЭС и АЭС.

Рисунок 1 – Выработка электроэнергии по территории

различными объектами генерации

Станции малой мощности, в том числе блок-станции, покрывают в основном базо-

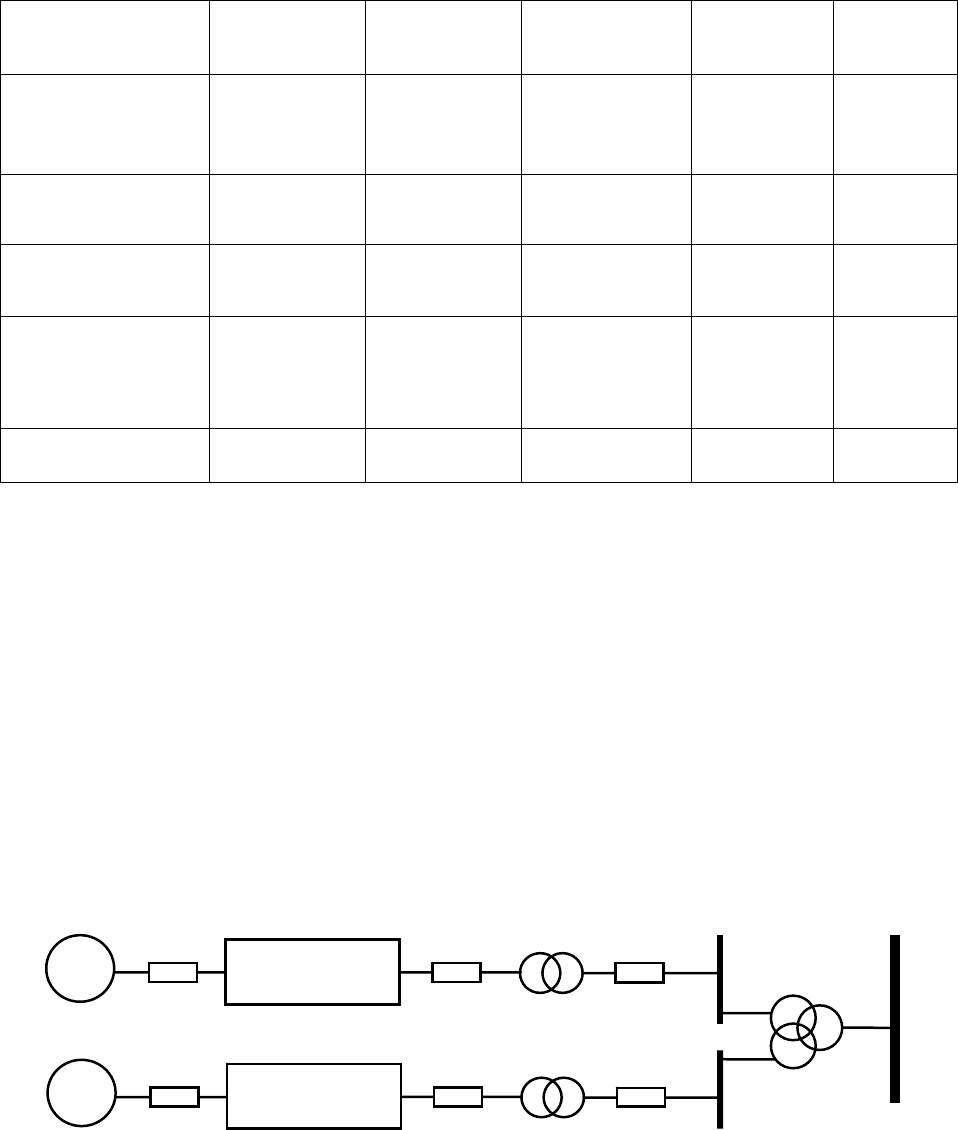
вую часть нагрузки. На рисунке 2 приведен типовой график нагрузки одной из станций

малой мощности, для которой коэффициент неравномерности составляет





min



max

⁄

0,875,

коэффициент формы





























ср

1,005.

Рисунок 2 – График нагрузки источника распределенной генерации

Объекты распределенной генерации представляют собой ГТ-ТЭЦ, ГТУ-генераторы, малые

гидравлические станции, станции на нетрадиционных источниках энергии и др. Источни-

ки РГ могут быть классифицированы по различным признакам, например:

 по типу технологии выработки энергии;

 по виду используемых первичных ресурсов;

 по виду подключения: непосредственное подключение к сети (электромеханиче-

ское) или инверторное подключение (через преобразователь частоты).

В таблице приведены основные технические характеристики наиболее распростра-

ненных источников РГ [1, 2].

0,0

1,0

2,0

3,0

4,0

5,0

6,0

7,0

8,0

1 163146617691106121136

372

Таблица – Основные технические характеристики источников РГ

Тип РГ

Дизельные ге-

нераторы

ГТУ ПГУ

Солнечные

установки

Ветреные

генераторы

Топливо

Продукты

переработки

нефти

Природный

и биогаз

Природный и

биогаз

Энергия

солнечного

света

Энергия

ветра

Возможность ра-

боты по графику

Возможно Возможно Возможно

Ограни-

чена

Ограни-

чена

Возможность

регулирования

Высокая Высокая Высокая Низкая Низкая

Установленная

мощность

Единицы

киловатт –

6 МВт

и более

0.1–30 МВт

и более

30 кВт–10 МВт До 1 МВт

0.1–2.5

МВт

КПД 30–45% 30–45% 20–40% 6–20% 1–35%

В условиях постоянного роста цен на электроэнергии и тепло в России наибольшее

распространение получили ПГУ, ГТ-ТЭЦ, ГТУ единичной мощности от 0,5 до 15 МВт.

Большинство источников распределенной генерации для крупных промышлен-

ных потребителей подключаются к основной распределительной сети через преобразо-

ватель частоты, так как в этом случае возможно уменьшение площади, занимаемой га-

зотурбинной электростанцией. Генератор выдает параметры переменного тока с часто-

той 100 Гц.

Типовая схема подключения блока турбина-генератор к распределительной сети

6(10) кВ имеет свои особенности. Выводы статорной обмотки генератора отделены от ос-

новной распределительной сети следующими элементами: коммутационным оборудова-

нием; преобразователями частоты; реакторами для ограничения токов коммутации преоб-

разователя; силовыми трансформаторами. Принципиальная схема подключения блоков

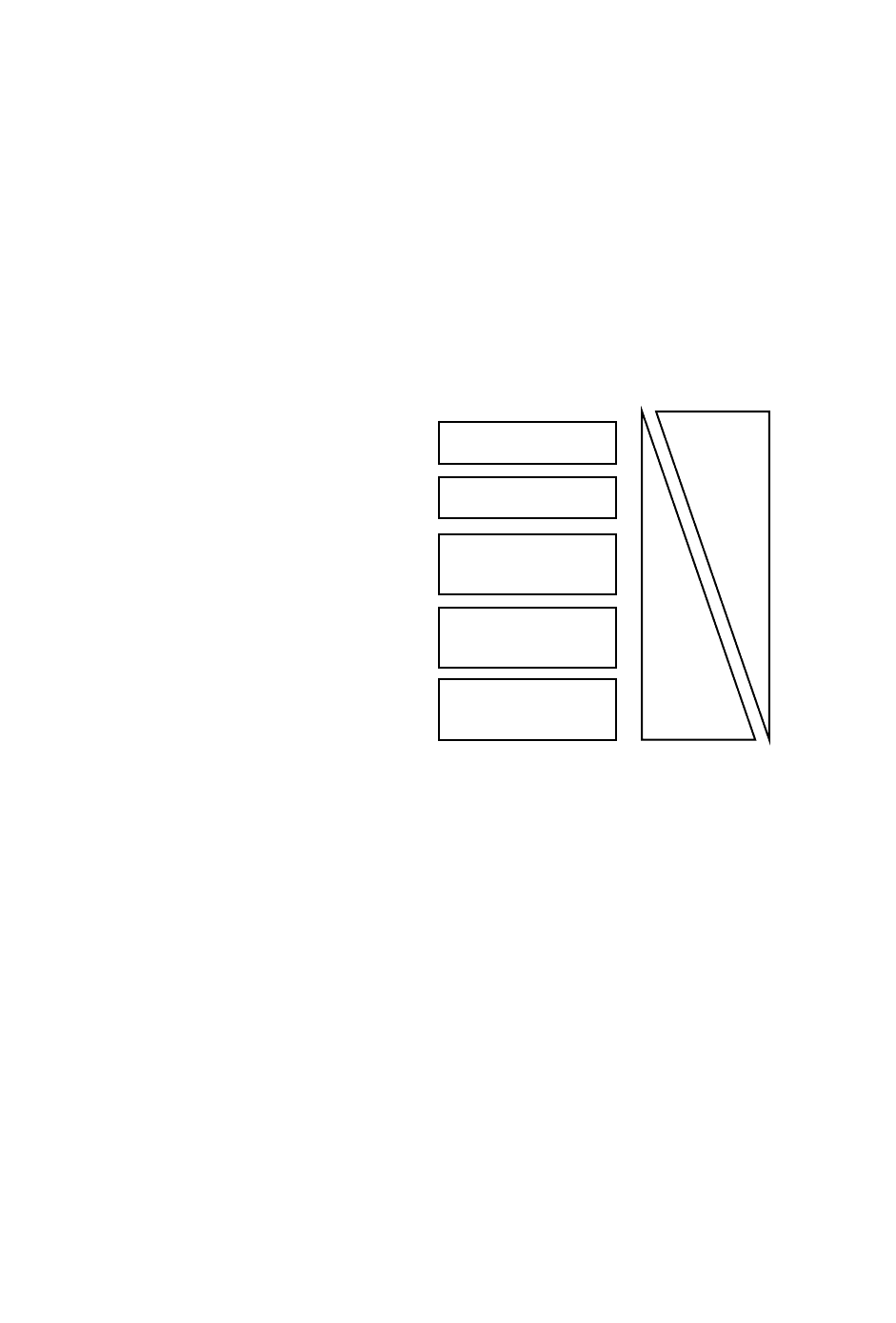
турбоагрегат–генератор малой мощности показана на рисунке 3.

Рисунок 3 – Структурная схема источника распределенной генерации:

Г – генератор; ПЧ – преобразователь частоты; В/И – выпрямитель/инвертор;

ЗПТ – звено постоянного тока; Р – реактор; Т – силовые трансформаторы

Инвестиционную привлекательность источника распределенной генерации предла-

гается оценивать с использованием математической модели, для которой определяются

оптимальное соотношение между инвестициями и издержками, влияние РГ на режимные

параметрами электроэнергетической системы, а также риски потерь нормального функ-

ционирования источника – минимизация ущерба от перерывов в электроснабжении.

Основная РС

110 кВ

Г1

ПЧ:

В/И, ЗПТ, В/И

Г2

ПЧ:

В/И, ЗПТ, В/И

6(10)/110 кВ

373

Для укрупненной оценки строительства РГ формируется математическая модель,

для которой главными факторами являются повышение надежности электроснабжения и

качества электроэнергии. Модель представлена следующими составляющими.

1. Стоимость приведенных затрат для собственной генерации





min



РГ

α

экс,ам



РГ



топл,ЭЭ











, (1)

где   стоимость удельных капиталовложений в тыс.руб. за 1 кВт установленной мощ-

ности РГ; α

экс,ам

– ежегодные издержки; 

топл,ЭЭ

– стоимость покупного топлива и элек-

троэнергии в год; 









– снижение издержек, связанных с уменьшением объема покуп-

ной тепловой и электрической энергии за тот же период; 

max



РГ





2. Повышение качества электроснабжения – снижение суммарного времени откло-

нений по напряжению





min





∆





ном













min





∆

∆





, (2)

где 

∆

– дополнительная прибыль, связанная с улучшением качества электроэнергии и,

соответственно, качеством и объемом выпускаемой продукции; ∆ – отклонение напря-

жения от номинального, которое приближенно определяется по формуле

∆





ном















ном

















ном







2

ном



. (3)

3. Оптимизация издержек на возмещение потерь электрической энергии за рас-

сматриваемый период:





min

∆

∆













min





∆

∆



. (4)

4. Повышение надежности электроснабжения – минимизация математического

ожидания от перерывов в электроснабжении [4]





minγ

∑





ωε, (5)

где ω – параметр потока отказов; γ – стоимость удельного ущерба от ограничения нагруз-

ки; ε – доля отключаемой нагрузки; 



– суммарное время нарушения электроснабжения.

Целевая функция включает вышеназванные составляющие с учетом весовых коэф-

фициентов, которые пока предлагается устанавливать экспертным путем.









minβ













β













β













β













, (6)

где β



β



β



β



1.

Значение коэффициентов зависит от требовательности потребителя к качеству

электроэнергии и необходимости обеспечения надежности и бесперебойности электро-

снабжения. Последний показатель является наиболее значимым, так как удельные ущербы

аварийного ограничения нагрузки для разных потребителей могут отличаться более, чем в

100 раз. Например, для открытой добычи угля удельный ущерб от аварийного ограниче-

ния

длительность до трех часов составляет около 0,5 долл. США/кВт·ч, а для предприятия

по переработки нефти – 40 долл. США/кВт·ч (данные взяты из [5]).

Для приближенной оценки стоимости установки одного киловатта мощности ис-

точника распределенной генерации принято значение 20 тыс.руб. за 1 кВт, что соответст-

вует 850 долл. США за 1 кВт установленной мощности, значения

удельных ущербов мо-

гут быть приняты в соответствии c видом промышленного производства [5], значения па-

374

раметров потока отказов пока предлагается принимать по данным, полученным на осно-

вании опыта эксплуатации в целом для установки.

Предлагаемая модель учитывает только часть особенностей и ситуаций, возни-

кающих при оценке влияния распределенной генерации на свойства ЭЭС. Отдельной про-

блемой для рационального развития и управления электроэнергетических систем с рас-

пределенной генерацией является разработка принципов оптимизации режимов, которые

должны учитывать новые регулирующие свойства энергопотребителей и их независи-

мость от диспетчерских решений.

Дальнейшие исследования позволят получить количественные оценки эффективно-

сти и инвестиционной привлекательности установок распределенной генерации с учетом

рисков ее использования.

Список использованных источников

1. Стофт С. Экономика энергосистем. Введение в проектирование рынков электроэнер-

гии: Пер. с англ. М.: Мир, 2006. 623 с.

2. Воропай Н.И. Распределенная генерация в электроэнергетических системах // Между-

народная научно-практическая конференция «Малая энергетика-2005», 2005.

3. Guan F.H. Research on Distributed Generation Technologies and its impacts on Power Sys-

tem // F.H. Guan , D.M Zhao, X. Zhang, B.T Shan, Z. Liu. Conference Proceedings DRPT.

China, 2008. 08DRPT0557.

4. Будовский В.П. Риск дефицита мощности энергосистемы // Электричество. 2009. № 8.

С. 12–17.

5. Непомнящий В.А. Экономические проблемы повышения надежности электроснабже-

ния. Ташкент: Изд-во Фан, 1985. 200 с.

375

МЕТОДИКА ПРОГНОЗИРОВАНИЯ УЗЛОВЫХ ЦЕН

НА ЭНЕРГОРЫНКАХ

А.В. Крупский

Филиал ОАО «СО ЕЭС» Башкирское РДУ

Введение. С целью обеспечения системного подхода при прогнозировании узловых

цен на электроэнергию автор разработал методику прогнозирования цен на электроэнер-

гию на оптовых энергетических рынках. Методика включает в себя следующие шаги:

1. Отбор факторов, оказывающих наиболее важное влияние на узловую цену на

оптовом рынке электроэнергии.

2. Проведение корреляционного и факторного анализа и уменьшение размерности

задачи.

3. Разработка моделей с учетом наиболее существенных факторов.

4. Расчет параметров выбранной зависимости.

5. Прогнозирование узловых цен.

6. Анализ результатов.

В рамках применения методики прогнозирования узловых цен на электроэнергию

предлагается использование стандартных моделей авторегрессии и скользящего среднего

(далее – АРСС) для прогнозирования и модификация таких моделей за счет рассмотрения

дополнительных переменных также с последующим прогнозированием цен на электроэнер-

гию.

Представляется целесообразным рассмотреть следующие переменные в рамках кор-

реляционного и факторного анализа:

1. Значение температуры окружающего воздуха (максимальное, среднее и мини-

мальное по дням). В исследовании рассматривались значения температуры в за-

висимости от объема потребления. При большем объеме потребления значение

температуры приобретает больший весовой коэффициент.

2. Равновесный объем электроэнергии, торгуемый на бирже (почасовые значения).

3. Освещенность в городах – крупных потребителях электроэнергии (число свето-

вых часов в день).

4. Количество осадков в день.

Факторами, которые также могут оказывать влияние на уровень цен на электро-

энергию в более долгосрочном периоде времени, являются:

1. Либерализация рынка энергоносителей и стоимость топлива.

2. Расход топлива и типы электростанций.

3. Экономические индикаторы.

4. Выработка электроэнергии по видам топлива и соотношения выработки элек-

трической и тепловой энергии.

Для стандартных моделей АРСС дополнительный факторный анализ не проводил-

ся.

Для прогнозирования узловых цен и последующей дискредитации и расчета вероят-

ностей автором было разработано программное обеспечение на Visual Basic (Excel). Кроме

того, использовались следующие программные средства: Statistica, Matlab и др.

Планирование включения электростанций в работу. Предприятия электроэнер-

гетики, работающие в условиях либерализации, при планировании режима загрузки элек-

тростанций должны рассматривать возможность участия на бирже электроэнергии. Тради-

ционная задача планирования производства электроэнергии преобразуется в комплексную

376

задачу расчета доли электроэнергии, покупаемой на рынке электроэнергии, и вырабаты-

ваемой собственными станциями. Для этого необходим прогноз узловых цен (на день впе-

ред) на бирже электроэнергии.

Для поддержки принятия решений на рынке электроэнергии необходимо использо-

вание подхода, позволяющего производить анализ временных рядов узловых цен. С этой

целью должно быть рассчитано дерево сценариев, отражающее стохастические особенно-

сти прогнозных величин.

Процесс планирования инвестиций, включения блоков и торговли на бирже элек-

троэнергии требует исчерпывающего метода оптимизации с использованием современной

вычислительной техники. Комплексность и высокая сложность постановки вопроса плани-

рования не позволяет решить задачу единым методом. По этой причине планирование под-

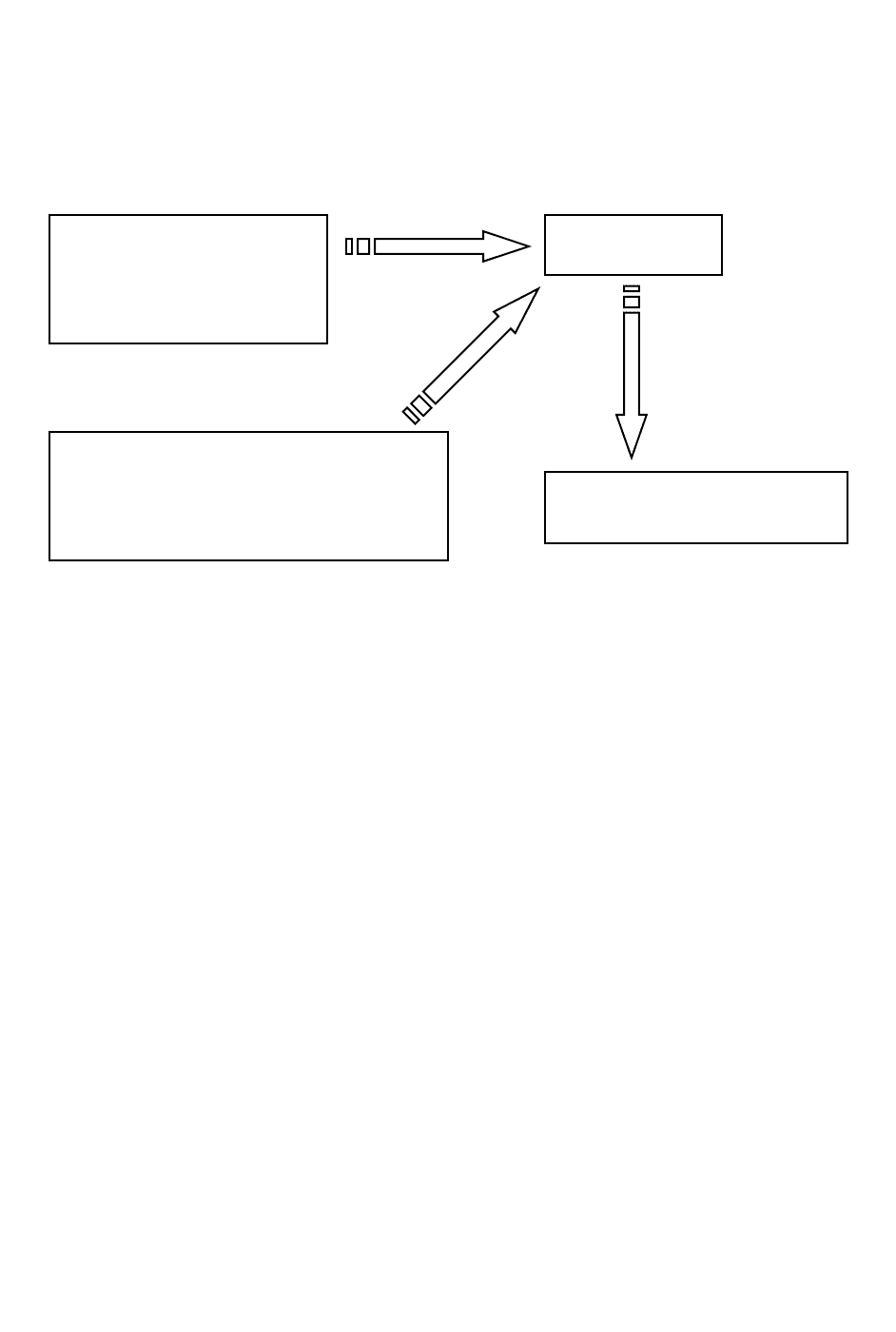
разделяется на многие иерархические частичные задачи (рисунок 1).

Рисунок 1 – Задачи планирования энергоснабжения

Планирование развития энергосистем является основой для возможных структур-

ных изменений отрасли с учетом стоимости инвестиций и эксплуатационных расходов, а

также выручки. В процессе планирования ревизий и ремонтов принимается решение о

плановой готовности. Оптимизация включения электростанций в работу определяет выра-

ботку электроэнергии с учетом среднесрочной торговли и на ее основании оптимизацию

стоимости и выручки. Как промежуточная ступень между долго- и краткосрочной торгов-

лей планирование включения электростанций в работу становится все более важным. Од-

нодневное планирование поддерживает решения о включении электростанций без быстро-

го старта и о торговле на бирже электроэнергии. В рамках распределения нагрузки опреде-

ляется режим работы уже включенных блоков и запуск блоков электростанций с быстрым

стартом.

С увеличением доли покупки и продажи электроэнергии на бирже электрические

мощности и связанные с ними расходы на производство электроэнергии становятся все

более подверженными влиянию рынка. При этом по контрактам на электроэнер-

гию/мощность с партнерами, располагающими установленной мощностью такого же по-

рядка, можно ожидать существенного увеличения объемов поставок электроэнергии.

Упомянутые выше процессы планирования сначала должны быть решены раздель-

но, но с учетом взаимовлияния и обратной связи между отдельными частями. В некоторых

случаях непредвиденные события приводят к необходимости нового расчета [4].

Строительство

Интервал

планирования

Задача

планирования

План ревизий

Включение

энергосистем

Включение

электростанций

Оперативное

планирование

>> 1 года

От 1 до 5 лет

1 год

От 1 до 7 дней

15 минут

детерминированно

стохастически

377

Особенности цен на электроэнергию. Объективность решений в планировании

зависит от многих факторов. На сегодняшний день стохастические компоненты при опти-

мизации включения электростанций в работу становятся все более важными. Общий про-

цесс оценки параметров представлен на рисунке 2.

К наиболее важным особенностям цен на электроэнергию относятся:

Рисунок 2 – Алгоритм принятия решения на основе вероятностей

 возврат к среднему значению (Mean Reversion): цены на электроэнергию возвра-

щаются к предыдущему среднему значению после завершения события, приведшего к рез-

кому отклонению;

 волатильность (Volatilitat): цены на электроэнергию обладают высокой вола-

тильностью, что связано с методом расчета (например, равновесная цена или цена самого

дорогого генератора). В данной работе в качестве фактора волатильности рассматривалась

дисперсия, которая играет существенную роль при определении стационарных интервалов

временных рядов. Такие интервалы обладают схожими уровнями отклонений цен. Необхо-

димо отметить, что чем выше абсолютный уровень цен, тем больше стандартное отклоне-

ние;

 сезонность (Saisonalitat): для цен на электроэнергию суточные, недельные и годо-

вые циклы сезонности выражены особенно сильно [1]. В настоящее время часто использу-

ются модели на основе синусоиды и модель, базирующаяся на коэффициентах, зависящих

от сезона. Автором данной работы предлагается использовать новую модель, учитываю-

щую актуальное значение температуры окружающей среды, которая в определенные мо-

менты времени может существенно отличаться от средней многолетней. Для временных

рядов были определены (псевдо)стационарные участки, корреляция на которых между тем-

пературой и объемом стремится к нулю. С целью обеспечения объективности результатов

расчета был проведен итеративный расчет с целью выявить среднюю длину интервала от-

дельно для каждого из сезонов года. Для вышеуказанных участков были вычислены сред-

ние значения температуры и определено изменение средней температуры от участка к уча-

стку. После проведения аналогичного расчета для ценовых значений была построена рег-

рессионная модель зависимости изменения цены от температуры. Оценки параметров рег-

рессионной модели были получены отдельно для положительных и отрицательных измене-

ний температуры;

 выбросы (Ausreisser): существенные краткосрочные отклонения от среднего уровня

цен.

 Торговый трафик

 График нагрузки

 Время ремонтов

 Договора на резервы

Детерминированное

плани

ование

Процесс

оценки

 События

 Модели

 Вероятностные критерии

 Принятие решения

 Спотовый рынок

 Аварии

 Отклонения от торгового графика

 Отклонения потребления

Стохастические

ез

льтаты

378

Прогнозирование. Ввиду сильной взаимозависимости между ценой электроэнер-

гии и соответствующим ей объемом представляется необходимым рассмотрение сущест-

вующих моделей прогнозирования электрической нагрузки. В настоящее время наиболее

часто используются следующие виды моделей:

1. Линейные и нелинейные системы.

2. Нейронные сети, в том числе в комбинации с моделями нечеткой логики.

3. Экспертные оценки.

В случае использования моделей, основанных на нейронных сетях, должен выпол-

няться ряд условий для получения адекватного результата. Условиями применимости ней-

ронных сетей являются: достаточная величина выборки с целью прогнозирования; отсут-

ствие выбросов либо ошибок во входных данных; качественное постоянство факторов,

влияющих на искомую величину; правильность определения числа промежуточных слоев

нейронной сети, числа элементов в каждом из них, а также алгоритма (например, с обрат-

ным распространением). Обычным требованием к прогнозу временных рядов для одного

периода времени является наличие данных в предыдущих четырех интервалах.

В дальнейшем предполагается использование расширенной математической модели

для создания прогноза почасовых узловых цен на электроэнергию на период до нескольких

месяцев. В качестве исходных данных были рассмотрены временные ряды почасовых узло-

вых цен и объемов электроэнергии, а также информация о погодных условиях в России для

2008–2009 годов.

Несколько параметров модели основываются на математической модели Карлоса

Бланко и Давида Соронова [3], отображающей такие свойства цен на электроэнергию как

возврат к среднему и стохастическое возникновение выбросов. К авторам, внесшим зна-

чительный вклад в моделирование цен на электроэнергию, относятся: Пирронг Г. и Жер-

макуйян Г., Еллиот Р.Д., Шварц Е., а также Клевлов Л. и Стрикланд С.

Итоговая разработанная модель может быть представлена в следующем виде:





∆















 θ







θ













σε



√

∆

 η









δε





ω













∆







(1)

где 



– узловая цена  в момент времени ;  – константа;  – коэффициенты авторегрес-

сии; θ – коэффициенты скользящего среднего; σ – дисперсия диффузионного процесса;  –

порядок авторегрессии;  – порядок скользящего среднего; η – случайная величина (далее

– с.в.), равная «1» в случае выброса и «0» в противном случае; ,δ – ожидаемая величина

выброса и стандартное отклонение выброса; ε



, ε



– две нормально распределенных с.в.

для учета диффузионного процесса и выбросов; ,  – коэффициенты регрессии измене-

ния цены при изменении температуры;  – значение температуры воздуха, °С; ω – коэффи-

циенты сезонности.

По сути, представленная стохастическая модель – это суперпозиция нескольких слу-

чайных процессов, вносящих аддитивные вклады в узловую цену.

Таким образом, первые







слагаемых представляют собой смешанную модель

авторегрессии и скользящего среднего [2]. Следующее слагаемое правой части уравнения

определяет диффузию и белый шум в модели. Белый шум рассчитывается как допустимые

отклонения фактических значений от плановых (случайная величина, распределенная по

нормальному закону, и имеющая среднее, равное нулю). Два последних слагаемых отра-

жают соответственно выбросы в цене и регрессионную зависимость, воспроизводящую по-

месячную/квартальную сезонность. Отражение сезонности, как изменение цены в зависи-

379

мости от изменения температуры, применено впервые и позволило улучшить модель по

сравнению с используемой в похожих случаях синусоидальной моделью или аддитивной

моделью, предусматривающей добавление определенной константы в зависимости от се-

зона года. Синусоидальная модель позволяет учитывать периодично повторяющиеся со-

ставляющие, но без отражения влияния текущих факторов, например, значение температу-

ры, как фактор, обуславливающий уровень цены.

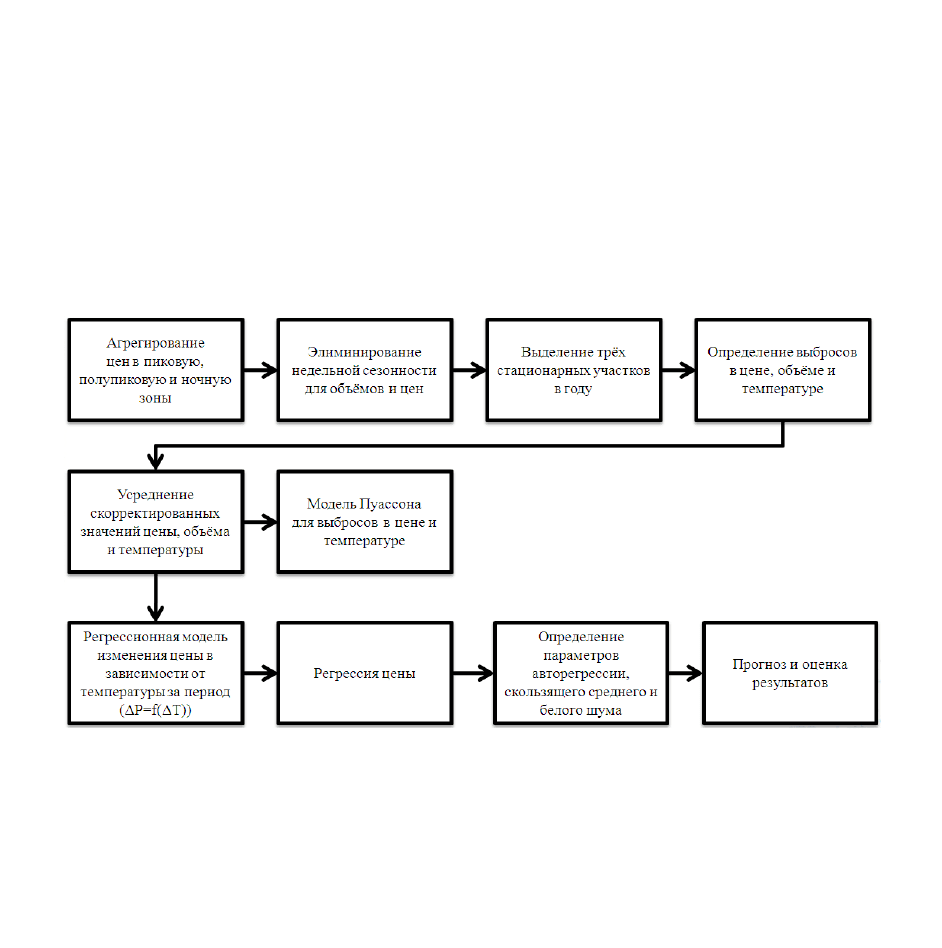
Общий порядок расчета параметров вышеуказанной модели представлен на рисунке 3.

Некоторые из представленных шагов являются итеративными, что улучшает показатели

качества модели. После элиминирования и учета сезонных компонент и выбросов была

рассчитана авторегрессионная модель со скользящим средним. На заключительном этапе

расчета был произведен прогноз узловых цен на электроэнергию и оценка результатов.

Рисунок 3 – Методика прогнозирования узловых цен на электроэнергию

Выводы. Представленная в данной работе методика прогнозирования узловых цен

может быть использована покупателями и производителями электрической энергии для

оптимизации работы на бирже электроэнергии. Знание прогноза узловых цен и вероятно-

стей реализации их сценариев необходимо для оптимизации заявок на торгах электро-

энергии, снижения рисков, связанных с колебанием и неопределенностью рыночной цены

на электроэнергию.

Список использованных источников:

1. Горячева И.П., «Некоторые проблемы учета сезонного фактора при построении индек-

сов потребительских цен». Вопросы статистики №10. М. 2004.

2. Box G., Jenkins G., «Time series analysis». Prentice-Hall. 2004.

3. Blanco C., Soronov D., «Energy price processes», Commodities Now. 2001.

4. Hoffmann J., «Optimale Energieeinsatzplanung in industriellen KWK-Systemen». ABEV. Aa-

chen 2006.

5. Pirrong C., Jermakyan M., «The price of power - the valuation of power and weather deriva-

tives» London. 2007.