Савицкая Г.В. Анализ хозяйственной деятельности предприятия

Подождите немного. Документ загружается.

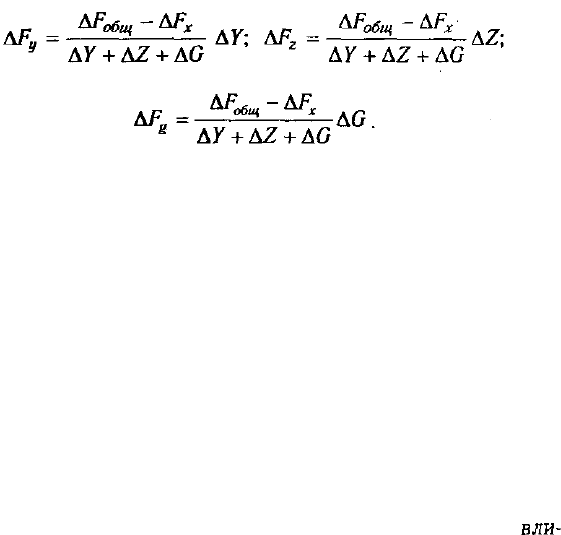
Глава 6. Способы измерения влияния факторов в ДФА 121

Таким образом, использование интегрального метода не тре-

бует знания всего процесса интегрирования. Достаточно в го-

товые рабочие формулы подставить необходимые числовые

данные и сделать не очень сложные расчеты с помощью каль-

кулятора или компьютера в Excel. При этом достигается бо-

лее высокая точность расчетов.

6.7. Способ логарифмирования в анализе

хозяйственной деятельности

Сущность, сфера применения и отличительные черты

способа логарифмирования. Алгоритмы расчета влияния

факторов этим способом.

Способ логарифмирования применяется для измерения

вли-

яния факторов в мультипликативных моделях. В данном слу-

чае результат расчета, как и при интегрировании, не зависит от

месторасположения факторов в модели и по сравнению с ин-

тегральным методом обеспечивается еще более высокая точ-

ность расчетов. Если при интегрировании дополнительный при-

рост от взаимодействия факторов распределяется поровну

между ними, то с помощью логарифмирования результат совме-

стного действия факторов распределяется пропорционально

доли изолированного влияния каждого фактора на уровень ре-

зультативного показателя. В этом его преимущество, а недоста-

ток — в ограниченности сферы применения.

В отличие от интегрального метода при логарифмировании

используются не абсолютные приросты показателей, а индек-

сы их роста (снижения).

Математически этот метод описывается следующим обра-

зом. Допустим, что результативный показатель можно предста-

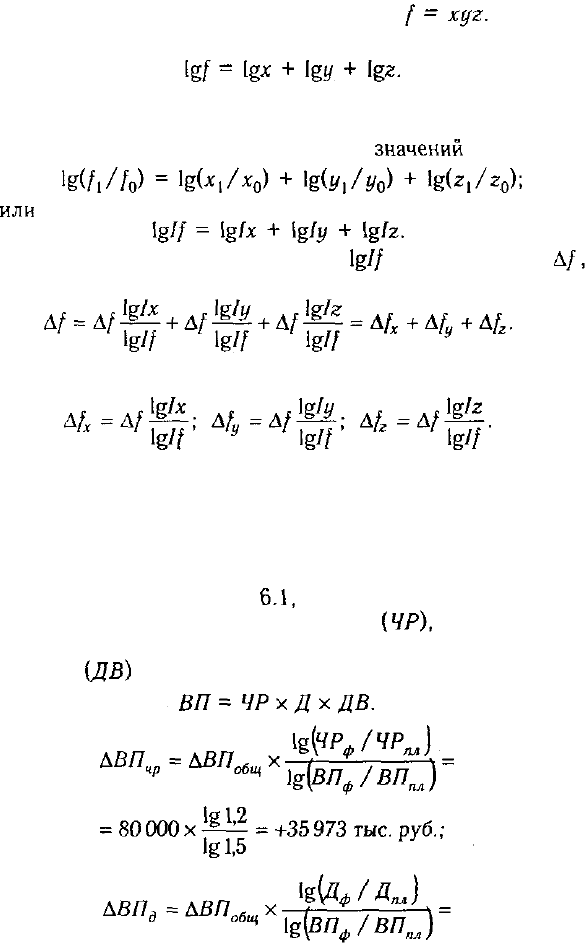
122

Часть I. Теория АХД

вить в виде произведения трех факторов: Пролога-

рифмировав обе части равенства, получим

Учитывая, что между индексами изменения показателей

сохраняется та же зависимость, что и между самими показате-

лями, произведем замену абсолютных их

значений

на индексы:

или

Разделив обе части равенства на и умножив на

получим:

Отсюда влияние факторов определяется следующим образом:

Из формул вытекает, что общий прирост результативного

показателя распределяется по факторам пропорционально от-

ношениям логарифмов факторных индексов к логарифму ин-

декса результативного показателя. И не имеет значения, какой

логарифм используется — натуральный или десятичный.

Используя данные табл.

6.1,

вычислим прирост валовой

продукции за счет численности рабочих

{ЧР),

количества от-

работанных дней одним рабочим за год (Д) и среднедневной

выработки

{ДВ)

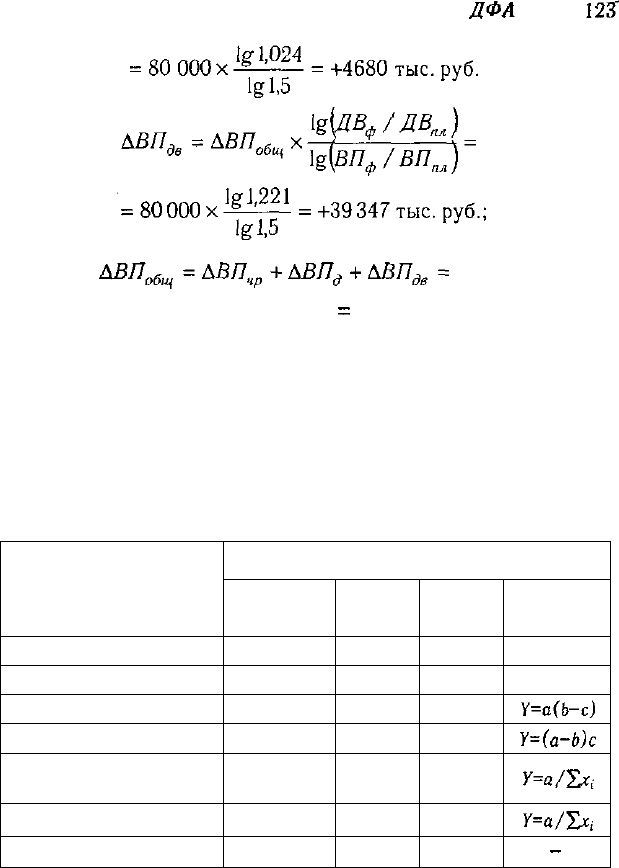
по факторной модели:

Глава 6. Способы измерения влияния факторов в

ДФА

123"

= 35 973 + 4680 + 39 347

80 000 тыс. руб.

Сравнив полученные результаты расчета влияния факто-

ров разными способами по данной факторной модели, можно

убедиться в преимуществе способа логарифмирования. Это вы-

ражается в относительной простоте вычислений и повышении

точности расчетов.

Рассмотрев основные приемы детерминированного фактор-

ного анализа и сферу их применения, результаты можно си-

стематизировать в виде следующей матрицы:

Прием

Цепной подстановки

Индексный

Абсолютных разниц

Относительных разниц

Пропорционального деле-

ния (долевого участия)

Интегральный

Логарифмирования

Модели

Мультипли-

кативные

Адди-

тивные

Кратные

Смешан-

ные

Y=a(b-c)

Y=(a-b)c

Y=a/lsi

Y=a/?Si

Знание сущности данных приемов, области их применения,

процедуры расчетов — необходимое условие квалифицирован-

ного проведения количественных исследований.

Глава 7

Понятие сто-

хастической

связи.

Задачи корре-

ляционного

анализа.

Способы изуче-

ния парной

корреляции.

Методика

множественного

корреля-

ционного

анализа.

Методика

оценки

и практического

применения

результатов

корреляцион-

ного анализа.

СПОСОБЫ ИЗУЧЕНИЯ

СТОХАСТИЧЕСКИХ

(КОРРЕЛЯЦИОННЫХ)

СВЯЗЕЙ

ВАНАЛИЗЕ

ХОЗЯЙСТВЕННОЙ

ДЕЯТЕЛЬНОСТИ

7.1. Понятие стохастической

связи и задачи корреляционного

анализа

Сущность стохастических взаимо-

связей между показателями. Отли-

чия стохастических связей от фун-

кциональных. Способы исследования

зависимостей в стохастическом

факторном анализе. Условия приме-

нения и задачи корреляционного

анализа.

В предыдущих главах рассматривалась

методика решения задач детерминирован-

ного факторного анализа. Однако на прак-

тике далеко не все экономические явле-

ния и процессы могут изучаться с помо-

щью этой методики, так как в большинстве

случаев их нельзя свести к функциональ-

ным зависимостям, когда величине фак-

торного показателя соответствует един-

ственная величина результативного пока-

зателя.

Чаще в экономических исследованиях

встречаются стохастические зависимос-

ти, которые отличаются приблизительно-

стью, неопределенностью. Они проявля-

Глава 7. Способы изучения стохастических связей 125

ются

только в среднем по значительному количеству объек-

тов (наблюдений). Здесь каждой величине факторного пока-

зателя (аргумента) может соответствовать несколько значе-

ний результативного показателя (функции). Например, увели-

чение фондовооруженности труда рабочих дает разный прирост

производительности труда на разных предприятиях даже при

очень выравненных прочих условиях. Это объясняется тем, что

все факторы, от которых зависит производительность труда, дей-

ствуют в комплексе, взаимосвязанно. В зависимости от того,

насколько оптимально сочетаются разные факторы, будет неоди-

наковой степень воздействия каждого из них на величину ре-

зультативного показателя.

Взаимосвязь между исследуемыми факторами и результатив-

ным показателем

проявится

если взять для исследования боль-

шое количество наблюдений (объектов) и сравнить их значе-

ния. Тогда в соответствии с законом больших чисел влияние

других факторов на результативный показатель сглаживает-

ся, нейтрализуется. Это дает возможность установить связь, со-

отношения между изучаемыми явлениями.

Значит, корреляционная (стохастическая) связь — это

неполная, вероятностная зависимость между показа-

телями, которая проявляется только в массе наблю-

дений. Отличают парную и множественную корреляцию.

Парная корреляция — это связь между двумя показателя-

ми, один из которых является факторным, а другой — результа-

тивным. Множественная корреляция возникает от взаимодей-

ствия нескольких факторов с результативным показателем.

Для исследования стохастических зависимостей использу-

ются следующие способы экономического анализа, с которы-

ми мы уже знакомились в предыдущих главах: сравнение па-

раллельных и динамических рядов, аналитические группировки,

графики. Однако они позволяют выявить только общий харак-

тер и направление связи. Основная же задача факторного ана-

лиза — определить степень влияния каждого фактора на уро-

вень результативного показателя. Для этой цели применяются

способы

корреляционного,

дисперсионного, компонентного,

дискриминантного,

современного многомерного факторно-

анализа и т.д.

126 Часть I. Теория

Наиболее широкое применение в АХД нашли приемы ко

реляционного анализа, которые позволяют количественно

вц,

разить взаимосвязь между показателями.

Необходимые условия применения

корреляциони

анализа.

1. Наличие достаточно большого количества

наблюде

и#

о величине исследуемых факторных и результативных

поь

за]

телей (в динамике или за текущий год по совокупности

до-

родных объектов).

2. Исследуемые факторы должны иметь количественное изме-

рение и отражение в тех или иных источниках информации.

Применение корреляционного анализа позволяет ре-

шить следующие задачи:

1) определить изменение результативного показателя под

во*

действием одного или нескольких факторов (в абсолютном из-

мерении), то есть определить, на сколько единиц изменяется

вели-

чина результативного показателя при изменении факторного на

единицу;

2) установить относительную степень Зависимости результа-

тивного показателя от каждого фактора.

Исследование корреляционных зависимостей имеет

огром!

ное значение в АХД. Это проявляется в том, что

значитель!

но углубляется факторный анализ, устанавливаются место и

роль каждого фактора в формировании уровня исследуемых

показателей, углубляются знания об изучаемых явлениях,

оп-

ределяются-закономерности

их развития и как итог — точнее

обосновываются планы и управленческие решения,

более!

объективно оцениваются итоги деятельности предприятий

более полно определяются внутрихозяйственные резервы. .

7.2. Использование способов парной корреляции

для изучения стохастических зависимостей

Формы стохастической связи. Приемы обоснования урав-

нения связи. Порядок расчета параметров уравнения пря-

мой, параболы, гиперболы. Методика расчета коэффициен-

тов корреляции при прямолинейной и криволинейной формах

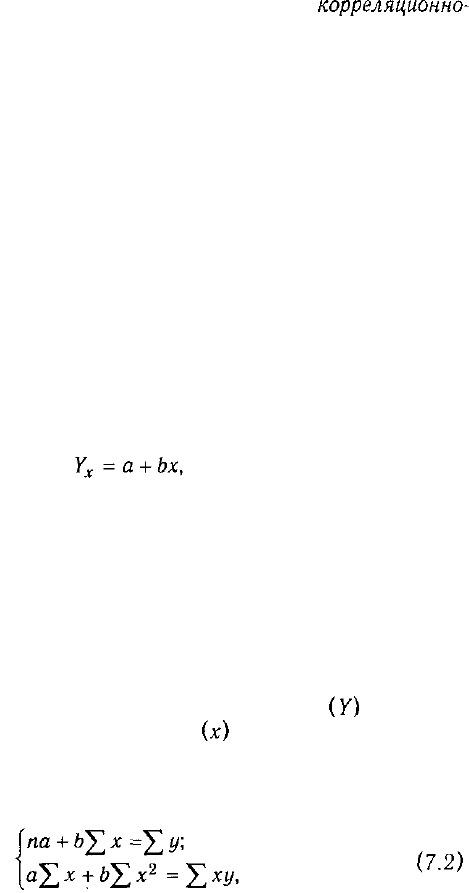
Глава 7. Способы изучения стохастических связей 127

зависимости. Интерпретация результатов

корреляционно-

регрессионного анализа.

Одной из основных задач корреляционного анализа явля-

ется определение влияния факторов на величину результатив-

ного показателя (в абсолютном измерении). Для решения

этой задачи подбирается соответствующий тип математичес-

кого уравнения, которое наилучшим образом отражает харак-

тер изучаемой связи (прямолинейной, криволинейной и т.д.).

Это играет важную роль в корреляционном анализе, потому

что от правильного выбора уравнения регрессии зависит ход

решения задачи и результаты расчетов.

Обоснование уравнения связи делается с помощью

сопоставления параллельных рядов, группировки данных и ли-

нейных графиков. Размещение точек на графике покажет, ка-

кая зависимость образовалась между изучаемыми показателя-

ми: прямолинейная или криволинейная.

Наиболее простым уравнением, которое характеризует

прямолинейную зависимость между двумя показателями, явля-

ется уравнение прямой:

(7.1)

где х — факторный показатель; Y — результативный показа-

тель; а и Ъ — параметры уравнения регрессии, которые требу-

ется отыскать.

Это уравнение описывает такую связь между двумя призна-

ками, при которой с изменением факторного показателя на

определенную величину наблюдается равномерное возрастание

или убывание значений результативного показателя. В каче-

стве примера для иллюстрации корреляционного анализа пря-

молинейной зависимости могут быть использованы сведения

об изменении урожайности зерновых культур

(Y)

в зависи-

мости от качества пахотной земли (см. табл. 4.7).

Значения коэффициентов а и Ь находят из системы урав-

нений, полученных по способу наименьших квадратов. В дан-

ном случае система уравнений имеет следующий вид:

где п — количество наблюдений (в нашем примере — 20).

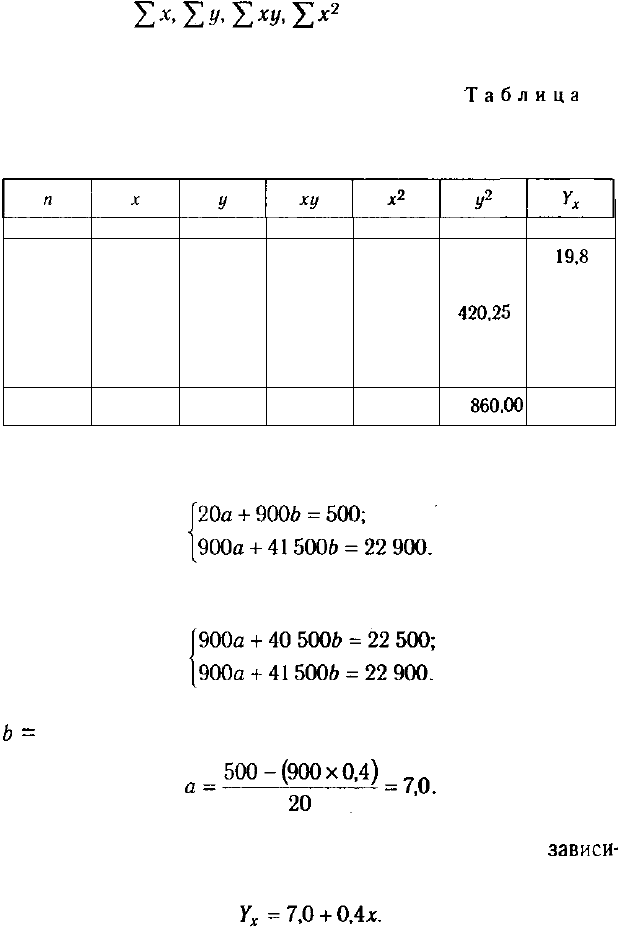
128

Часть I. Теория АХД

Значения рассчитываются на основе

фактических исходных данных (табл. 7.1).

Таблица

7.1

Расчет производных величин для определения

параметров уравнения

связи и коэффициента корреляции

Итого

32 .

900

19,5

19,0

20,5

33.0

500,0

624

627

717

1980

22 900

1024

1089

1225

3600

41 500

380,25

361.00

420,25

1089.00

860.00

19,8

20.2

21.0

31.0

500,0

Подставив полученные значения в систему уравнений, по-

лучим

Умножив все члены первого уравнения на 45 (900/20), по-

лучим следующую систему уравнений:

Отнимем от второго уравнения первое. Отсюда 10006 = 400;

0,4,

Таким образом, уравнение связи, которое описывает

зависи-

мость урожайности от качества почвы, будет иметь вид

Глава 7. Способы изучения стохастических связей 129

Коэффициент

а — постоянная величина результативного

показателя, которая не связана с изменением данного факто-

ра. Параметр b показывает среднее изменение результатив-

ного показателя с повышением или понижением величины

фактора на единицу его измерения. В данном примере с уве-

личением качества почвы на один балл урожайность зерновых

культур повышается в среднем на 0,4 ц/га.

Подставив в уравнение регрессии соответствующие значе-

ния х, можно определить выравненные (теоретические) значе-

ния результативного показателя (Y) для каждого хозяйства.

Например, чтобы рассчитать урожайность зерновых культур для

первого хозяйства, где качество почвы оценивается 32 баллами,

необходимо это значение подставить в уравнение связи:

7 + 0,4x32 = 19,8 ц/га.

Полученная величина показывает, какой была бы урожай-

ность при качестве почвы 32 балла, если бы данное хозяйство

использовало свои производственные возможности в такой

степени, как в среднем все хозяйства района. Аналогичные

расчеты сделаны для каждого хозяйства. Данные приведены

в последней графе табл. 7.1. Сравнение фактического уровня

урожайности с расчетным позволяет оценить результаты ра-

боты отдельных предприятий.

По такому же принципу решается уравнение связи при кри-

волинейной зависимости между изучаемыми явления-

ми. Если при увеличении одного показателя значения друго-

го возрастают до определенного уровня,

потом начинают

снижаться (например, зависимость производительности труда

рабочих от их возраста), то для записи такой зависимости

лучше всего подходит парабола второго порядка:

=a + bx + cx

. (7.3)

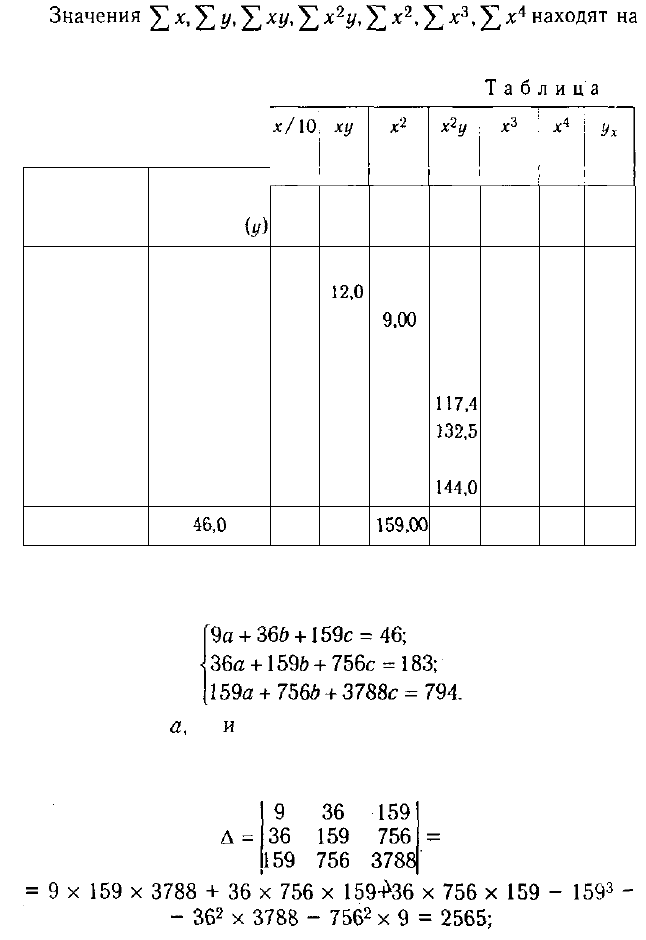
В соответствии с требованиями метода наименьших квадра-

тов для определения параметров a, b

с необходимо решить

следующую систему уравнений:

(7.4)

Зак/2049

130

Часть I. Теория АХД

основании исходных данных (табл. 7.2).

Таблица

7.2

Зависимость производительности труда

(у)

от возраста работников (х)

Средний

возраст по

группе {х)

Всего

Средне-

месячная

выработка

{у)

4,2

4,8

5,3

6,0

6,2

5,8

5,3

4,4

4,0

46,0

2,0

2,5

3,0

3,5

4,0

4,5

5,0

5,5

6,0

36,0

8,4

12,0

15,9

21,0

24,8

26,1

26,5

24,2

24,0

183,0

4,00

6,25

9.00

12,25

16,00

20,25

25,00

30,25

36,00

159,00

16,8

30,0

47,7

73,5

99,2

117,4

132,5

133,1

144,0

794,0

8,00

15,62

27,00

42,87

64,00

91,13

125,00

166,40

216,00

756,00

150

256

410

625

915

1296

3788

3,93

4,90

5,55

5,95

6,05

5,90

5,43

4,78

3,70

46,00

Подставив полученные значения в систему уравнений,

получим

Параметры

а,

с находят способом определителей или

способом исключения. Используем способ определителей.

Сначала найдем общий определитель: